铣削机器人去除锻件裂纹的轨迹规划研究
张永贵,李海龙
(兰州理工大学 机电工程学院,兰州 730050)
0 引言
大型锻件在锻造的过程中会产生裂纹,多次锻造中裂纹的存在会影响锻件质量,因此在每次锻后检查并去除裂纹非常重要。传统的去除方法是人工用角磨机打磨,这种方法的缺点是效率低、环境嘈杂、工人劳动强度大,采用铣削机器人加工可以代替人工,在达到高效环保的同时,对提升锻件质量具有现实意义。随着科学技术的不断发展,工业机器人在切削加工领域得到了广泛地应用。工业机器人将末端执行器变为具有铣削、磨削、钻削、雕刻等功能的主轴系统,就使机器人成为机加工机床[1],以机器人代替数控机床完成多轴切削加工具有作业范围大、安装空间小、集成度更高、经济效益和柔性更好等优点[2]。工业机器人基本的插补方法有直线插补和圆弧插补,然而锻件裂纹在空间中是一条自由曲线,运用直线和圆弧插补方式在加工的过程中会产生较大的代码段[3],而且由于自由曲线的特殊性,会使刀具在插补周期相邻处的速度和加速度不连续,使工业机器人产生振动,导致加工出的零件表面不光滑,因此在分析裂纹轨迹的基础上提出三次B样条曲线插补技术。在锻造的过程中,裂纹并不会一定出现,因此在每次锻后检查裂纹是否存在就成为主要问题。文献[4]给出了机器视觉识别裂纹轨迹的方法,通过该方法能够给出一系列笛卡尔空间的离散坐标点,用三次B样条曲线拟合这些离散点得到曲线p=p(u)。在运动规划中,u=u(t)描述了铣削机器人的末端执行器的运动规律。当轨迹在笛卡尔空间被完全确定后,通过机器人系统的逆运动学模型,将轨迹转换到关节空间,用速度、加速度等约束条件来控制机器人运动[5]。
目前国内外常用的插补算法有等参数插补算法[6]、恒速插补算法[7]、基于精度要求的插补算法[8],这些插补算法都未考虑机床或机器人的加减速特性,会影响加工质量。为了避免铣削机器人加工复杂曲线时在速度敏感点处发生速度突变引起的机器人末端执行器振动和切削加工的过切现象,本文提出梯形加减速控制算法与三次B样条曲线插补的融合算法,实现铣削机器人对复杂曲线的加工。
1 机器人末端铣刀路径规划

(1)
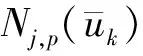
(2)
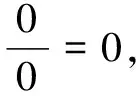
1.1 参数值的选取

(3)

(4)
节点矢量U由式(5)得:
(5)
1.2 反算控制点
已知(n+1)个数据点Qk,k=0,1…,n,则有(n+1)个未知的控制点Pk,为了得到Pk的唯一解,必须增加两个附加条件。由于曲线刚好在节点处插值于Qk,因此开始的两个方程和最后的两个方程分别为:
(6)
式中:
式(6)的这4个方程可以直接求解,由于每一个内节点处只有三个非零的三次基函数,所以剩下的(n-1)个方程可写成如下形式:
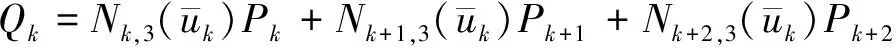

则可以得到三对角方程系统:
NP=R
(7)
式中,
对式(7)中的矩阵进行求解,再加上式(6)中求解出的4个方程可得到三次B样条曲线的控制点Pk,已知裂纹轨迹的基函数和三次B样条曲线的控制点就完全确定了机器人末端执行器的运动路径。
2 插补算法
2.1 进给速度规划
在机器人铣削的过程中,进给速度是影响加工质量的关键因素,只有保证进给速度稳定,才能保证裂纹去除的质量[9]。假定参数曲线的几何路径为:
P(u)=P(X(u),Y(u),Z(u))
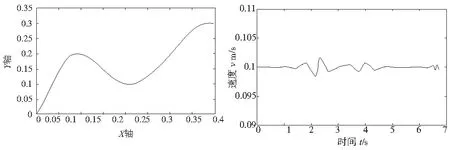
其中,时间函数u是曲线参数,u=u(t)表示机器人末端的运动规律。当加工如图1所示的三次B样条曲线的裂纹轮廓时,由于在曲线的极值点处会造成速度突变[10],如果采用传统的恒进给速度进行加工,会在极值点处出现过冲和机器人振动等现象,影响裂纹去除质量。
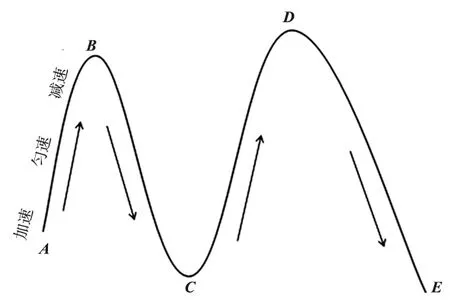
图1 速度规划图
在分析上述问题以后,提出梯形加减速控制方法。首先根据三次B样条曲线拟合出的路径找到曲率的极大值点,然后依据曲率极值点对该曲线进行分段,即图1所示的B、C、D三点,据此曲线被分成4段。以AB段为例,AB段分为加速、匀速、减速三个阶段,在曲线段的起点处,为提高加工效率必须尽可能地加速;在运动到曲率的极大值之前,必须进行减速;在AB段大部分的加工路径都是恒进给速度。其它曲线段的加减速控制与AB段相同,这种方法能够克服机器人末端刀具在曲线敏感点处由速度突变引起的振动和过冲现象,保证了加工质量。
2.2 梯形速度的生成算法
对于一个给定的控制系统,进给速度v和加速度a由人工给定,采样周期Ts通常是一个恒量。首先根据数值计算方法计算每段曲线的长度,然后根据给出的进给速度v和加速度a计算总的运动时间。梯形速度分为加速阶段、匀速阶段、减速阶段,其中加速阶段的运动时间为:
(8)
一般情况下s>vta,总的运动时间为:
(9)
其中,s为每段曲线起始点和终点之间的距离,ts为总的运动时间。
令采样周期数为k,vk为每个采样周期的进给速度,其中vk=v(kTs)。当在加速阶段时,t≤ta
(10)
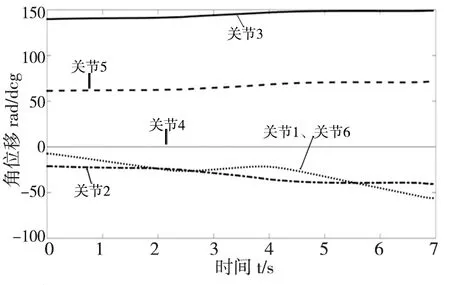
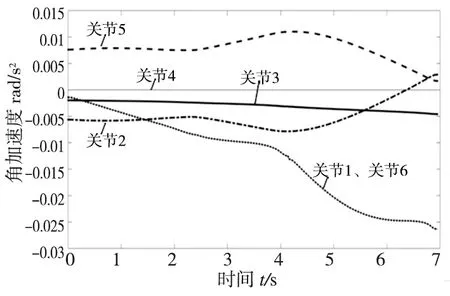
当在匀速阶段时,ta vk=v (11) 当长减速阶段时,ts-ta (12) 其中在减速阶段加速度a=-a。根据式(10)~式(12)就可以计算出每个采样周期的进给速度vk。 三次B样条曲线插补的实质是在每个采样周期内求取满足进给速度要求的参数增量Δu,然后代入三次B样条曲线表达式进行计算,得到采样周期内各个坐标轴的增量值。插补的问题可以转换为利用Taylor展开公式求下一时刻tk+1时参数uk+1的值。 沿着三次B样条曲线P(u)在每个插补周期的进给速度可以定义为: (13) 式中,u是关于时间t的函数,因此式(13)可以写成: (14) 式中,P(1)(u)表示三次B样条曲线的一阶导数,可以得到: (15) u(t)二阶导数为: (16) 式中,A(t)为每个采样周期的加速度,t=kTs。由当前参数uk利用Taylor展开公式计算出下一个插补周期的参数uk+1,通过计算每一插补点的基函数和控制点相乘计算出插补点的坐标值。Taylor展开公式为: (17) 由式(13)~式(17)可得到一阶、二阶三次B样条曲线插补公式分别为: (18) (19) (20) 将计算出的曲线参数uk和曲线P(u)的一阶导数代入式(20)就可以计算出实际进给速度,通过实际进给速度和规划进给速度的对比来分析此种插补算法是否合理。 对于机器人铣削来讲,将铣刀安装在机器人末端,控制机器人各关节按一定规律运动来完成工件表面的铣削。根据铣削工艺要求,铣削时铣刀垂直于工件表面,并且在铣刀的垂直方向给定一个进给量h,工作台的高度为1m,然后以进给率规划的速度对工件表面进行加工。该铣削机器人任务空间可以描述如图2所示,Σ0为机器人的基坐标系,ΣW为工件坐标系,ΣG为铣刀的附体坐标系。 图2 铣削加工示意图 本文采用标准的D-H模型建立机器人杆件附体坐标系,如图3所示为机器人D-H坐标系。机器人相邻两连杆的位姿关系用一个4×4的齐次坐标矩阵来描述,相邻坐标的D-H变换矩阵为: i - 1Ai=Rot(z,θi)Trans(z,θi)Trans(x,ai)Rot(x,αi) 将表1中的D-H参数带入相邻坐标的变换矩阵中,则机器人末端坐标系相对于基座系的位姿可以通过变换矩阵的连乘得到,其数学表达式为: (21) 图3 机器人D-H坐标系 则位姿矩阵0T6可以表示为: (22) 式中,nx、ny、nz、ox、oy、oz、ax、ay、az表示机器人末端的姿态,px、py、pz表示机器人末端的位置。 机器人刀具坐标系相对于工件坐标系的变换矩阵为式(23);任务空间的工件坐标系相对于机器人基坐标系的变换矩阵为式(24);机器人刀具坐标系相对于机器人附体坐标系的变换矩阵为式(25)。 (23) (24) (25) 式中,dG为末端铣刀的长度;h为铣刀垂直的进给量;xw0=-0.6971m,yw0=0.0196m,zw0=-0.9039m;因此,机器人末端执行器相对于基坐标系的位姿0T6可以表示为: (26) 将表1中的数据代入公式(26)中,可以计算出机器人刀具每一个插补点的齐次坐标矩阵,通过机器人逆解可以计算出机器人各个关节的位移量。 表1 机器人D-H参数 针对锻件表面裂纹去除的方法研究,为了验证算法的正确性,假定机器视觉识别的裂纹轨迹的型值点如表2所示。 表2 裂纹轨迹型值点 该运动路径有两个速度敏感点,如果采用恒进给速度进行加工得到的进给速度曲线如图5所示。 图4 末端执行器运动路径 图5 恒进给速度曲线 当机器人采用恒进给速度加工时,在机器人运动到速度敏感点时由于自由曲线的特殊性会使机器人末端执行器速度突变引起机器人振动,影响了切削加工质量。 因此采用梯形速度规划方法将机器人末端路径分为三段,通过数值计算方法计算每一段曲线的长度,计算的结果分别为L1=0.2230、L2=0.1697、L3=0.2696;将每段曲线取10个型值点再次参数化,求取每段曲线的控制点和基函数;规定机器人末端在笛卡尔空间最大速度v=0.1m/s、最大加速度为a=1m/s2,采样周期Ts=0.01s,将速度v、加速度a以及每段曲线长度分别代入梯形速度的生成算法中,计算出每个采样周期的进给速度vk;将规划出的进给速度vk代入到插补算法的计算公式中,计算出每个采样周期的参数值uk+1;每个采样周期的参数值uk+1可以确定机器人末端在笛卡尔空间的坐标和该点处P(uk+1)的一阶导数,通过公式(20)可以计算出机器人末端刀具的进给速度。根据以上的计算得到了机器人末端进给速度,如图6所示。 图6 梯形速度曲线 从图6可以看出,机器人末端执行器在速度敏感点处速度减至到零,然后再经历加速、匀速、减速阶段,该过程符合梯形速度规划要求,从而避免了机器人在速度敏感点处由速度突变引起的机器人振动。 已知机器人末端在每个采样周期的位置和姿态,就可以通过机器人逆解计算出机器人各个关节的位移变化量;已知机器人末端的速度,通过雅克比求逆可以计算出各关节角速度;已知雅克比矩阵和二阶影响系数矩阵可以求解各关节角加速度。图7为各关节角位移、角速度、角加速度图。 从图7可以看出机器人各关节角位移、角速度、角加速度均连续变化,说明笛卡尔空间的轨迹规划符合加工要求。 图7 各关节角位移、角速度、角加速度图 本文针对铣削机器人去除大型锻件裂纹的方法,采用三次B样条曲线拟合裂纹轨迹,拟合的曲线为机器人末端加工的路径,通过对路径的分析采用加减速控制方法按照给定的插补周期进行三次B样条插补,该方法能够避免加工时机器人在速度敏感点发生速度突变。通过实例验证和仿真证明该方法有效可行,对于提高加工质量具有现实意义。2.3 插补算法
3 机器人运动模型的建立
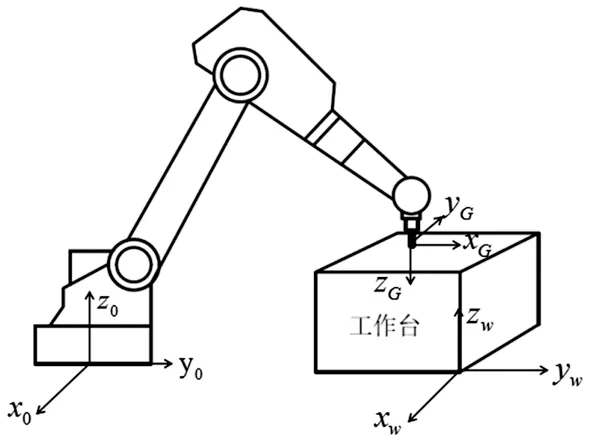
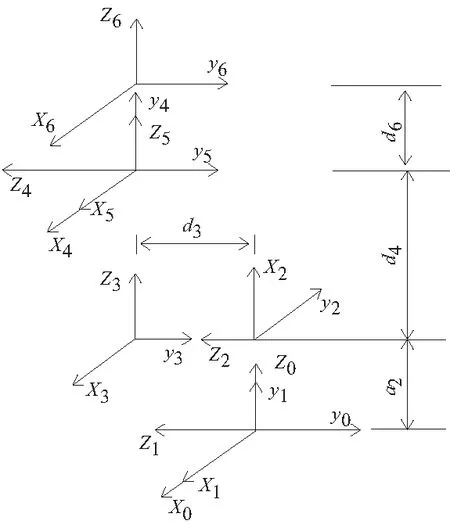
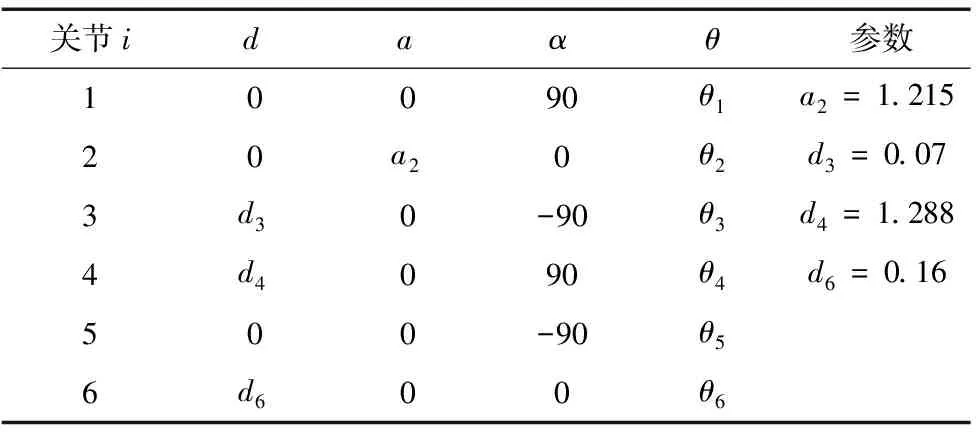
5 实例分析
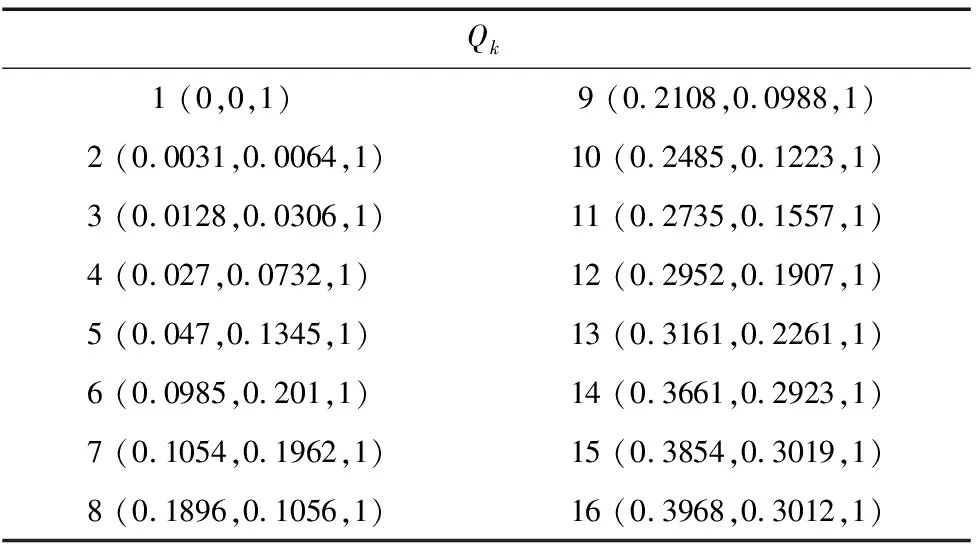


6 结论

