花岗岩变形破坏过程中不同细观组分的分形特征

周祥运，徐金明，刘绍峰

(上海大学土木工程系， 上海 200444)

0 引 言

花岗岩通常由长石、石英、黑云母等不同细观组分组成，岩石的变形破坏过程取决于这些细观组分的变化情况，这种变化可以使用不同组分的分形维数来表征。

使用分形方法研究岩土材料的变形破坏过程已经取得了很多进展，通常使用基于盒维数法的简单分形维数进行研究。比如，李长江等[1-2]使用滑坡空间分布的简单分形维数计算方法，进行滑坡易发程度的区划和评价，提出了不同尺度范围内降雨量—滑坡频度关系的分形；Pia等[3]提出了一种混合单元的分形模型，预测了多孔岩石的渗透性；李守臣等[4]建立了单轴压缩条件下岩石分形维数与岩石顶部位移的非线性演化模型；Li等[5]研究了岩石节理粗糙度系数与岩石结构表面分形维数之间的定量关系。将简单分形维数与数字图像处理技术相结合，彭瑞东等[6]对石灰岩拉伸过程中的扫描电子显微(SEM)图像计算分形维数，得到岩石表面分形维数随载荷增大而逐渐增大的结论；宫伟力等[7]探讨了煤岩细观裂隙计算机断层扫描(CT)图像分形维数与煤岩孔隙度的关系；陈世江等[8]用岩石节理图像分形维数和起伏度来描述节理的粗糙度系数；Liu等[9]研究了煤岩及其在甲烷吸附状态下的分形特性。

此外，采用以广义分形为基础的多重分形理论来研究岩土材料的变形破坏过程，也取得了一些进展。谢和平等[10]用改进投影覆盖法来测定岩石断裂表面的分形维数，分析了断裂表面的多重分形性质；刘树新等[11]使用多重分形方法研究岩石强度的Weibull参数，改进了岩石的损伤统计本构模型；许福乐等[12]用多重分形对煤岩声发射强度时间序列进行了分析，认为这一序列的波动特性是一个多重分形过程；蔡江东等[13]运用广义多重分形理论对受压破坏的声发射信号进行了分析，发现岩石加载初期与濒临破坏时声发射信号特征参数存在显著差异；邹飞等[14]用广义多重分形理论对类岩石材料表面损伤的演化进行了描述，分析了图像灰度相关性系数分布演化与试件表面变形局部化在时域和空域的对应关系。

现有研究成果中，分形维数多使用基于盒维数法的简单分形维数、而广义分形维数和多重分形维数考虑不多，计算分形维数时难以考虑多种组分分布的细节，分形维数随加载水平增加而变化的具体过程也考虑得不多。本文拟以花岗岩为例，根据岩石室内试验过程中拍摄得到的试验视频，使用数字图像处理技术提取任一加载时刻岩石中不同细观组分的实际位置，研究不同细观组分分形维数随时间的变化过程，为进一步研究岩石的变形破坏机理打好基础。

1 室内抗压强度试验

1.1 试验方法

试样取自甘肃北山的花岗岩。经过室内切割制成50 mm × 50 mm × 100 mm的试块，按照国际岩石力学试验规程对试样两端面及侧面进行仔细打磨，试样断面平整度及侧面平整度分别为0.02 mm、0.3 mm。

采用RMT-150C型岩石力学伺服试验系统进行室内抗压强度试验。试验前，在试样周围布置三台型号为佳能600D的摄像机(最大像素和有效像素分别为1 870万和1 800万、最高分辨率为5 184 × 3 456)，一台摆在试样的正面位置，其余两台摆放在试样的侧面位置。试验过程采用位移控制，加载速率控制为0.006 mm/s，连续加载直至试样完全破坏。使用摄像机拍摄整个试验过程，得到试验视频图像。视频图像的记录格式为MOV。

1.2 试验结果

图1中σmax为峰值应力，由图1和图2可以看出，在加载初期，岩样没有发生明显变形；应力水平为0.35σmax时，岩样左侧中部出现第一条主裂隙，裂隙从试件中部向两端扩展，发生纵向破坏；应力水平为0.65σmax时，裂隙已经扩展到两端，把试件分割成左半部的小试块和右半部的岩样主体部分，岩样上部被迅速压密、并出现脱落；应力水平为0.90σmax时，岩样右半部出现了第二条主裂隙，裂隙从中部出发、扩展到贯穿试件右半部。

图1 不同加载水平时的花岗岩试件外观图Fig.1 Outlines of granite specimen at different load stages

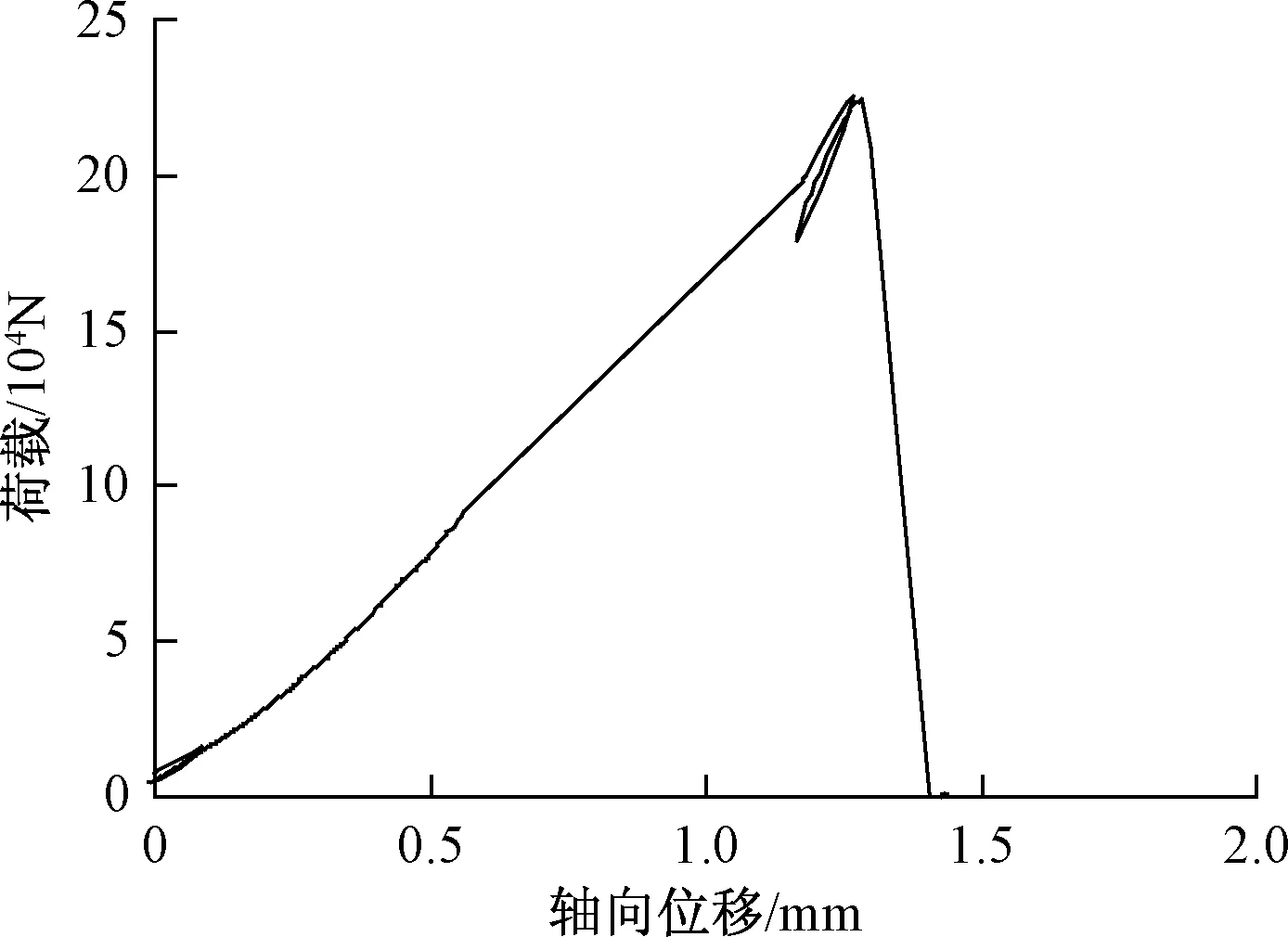
图2 花岗岩试件的荷载-轴向位移曲线Fig.2 Load-axial displacement curve of granite sample

2 分形维数计算方法

2.1 简单分形维数

采用计盒维数法计算花岗岩视频图像的简单分形维数。计算公式为：

(1)

式中：ε——正方形盒子边长；

N——盒子个数。

在双对数坐标平面内，以直线拟合数据点(logε，logN)，直线斜率负值D就是简单分形维数。具体计算时，把花岗岩图像进行二值化处理，使每一个像素点用黑色或白色表示(即黑色代表0、白色代表1)，用边长为ε的正方形盒子覆盖图像区域，统计包含有1的盒子个数N，采用不同大小的ε(这里ε=2，3，4，…，100)覆盖图像区域，得到盒子数N2，N3，N4，…，N100，根据式(1)得到分形维数。

2.2 广义分形维数

广义分形维数的计算公式为：

(2)

式中：q——是权重因子，研究时取|q|max=4(孙霞[15]等)；

τ(q)——质量指数；

Xq(ε)——为配分函数。

由式(3)计算

(3)

式中：Pij(ε)——图像区域的概率集。

得到Pij(ε)的方法为：用不同大小ε的正方形盒子去覆盖图像，计算每个盒子(i，j)中对象区域的像素数nij除以全部对象区域的总像素数∑nij，就得到每个盒子中对象区域占据的概率Pij(ε)。本次研究，取广义分形维数谱的最大值Dmax和最小值Dmin作为不同细观组分广义分形维数谱的度量。Dmin主要反映组分区域中小面积区域的变化情况，Dmax主要反映组分区域中大面积区域的变化情况。

2.3 多重分形维数

研究多重分形维数时，首先获得多重分形谱f(α)。f(α)的计算公式为：

(4)

式中：α——奇异性指数；

f(α)——为多重分形谱。

对τ(q)和q作勒让德变换得到多重分形谱f(α)。

研究时用多重分形谱f(α)的不均匀指数A和形状指数B来表征细观组分的多重分形特征。A定义为f(α)的谱宽、即A=αmax-αmin，反映了各组分区域概率测度分布的不均匀性程度。B定义为B=f(αmin)-f(αmax)，是各组分最大与最小区域概率的差值，是组分区域复杂程度、不规则程度和不均匀程度的度量，反映了多重分形谱的形状特征。

3 不同组分分形维数的变化特征

3.1 不同细观组分分布的确定

试验视频延时6分58秒。研究时，采用MATLAB平台、通过编制程序代码来实现不同变形破坏阶段分形维数的计算。为了便于编程处理，将试验视频由MOV格式转化为AVI格式。编程处理时，把图像剪裁得到120 × 360像素的图像区域，将未发生破坏到破坏、共6.00 s(原视频247～253 s)的所有帧图像组成新视频。

将试件表面产生裂隙的时刻作为变形阶段和破坏阶段的分界时刻，根据裂隙出现的多少把岩石变形破坏过程分成变形阶段(没有裂隙)、破坏时裂隙较少(只存在第一条裂隙)、破坏时裂隙较多(多条裂隙存续时段)等三个阶段。三个阶段在原视频中对应的时刻(应力水平)分别为247～250 s(0.32σmax～0.36σmax)、250～251 s(0.36σmax～0.38σmax)、251～253 s(0.38σmax～0.40σmax)。为减少计算量，每隔5帧抽取一幅图像进行研究。

新视频中花岗岩试样应力、累计位移与时间的变化图见图3。

图3 花岗岩试件应力、累计位移与时间关系图Fig.3 Variations of stress and accumulative displacement with time of granite specimen

采用点选统计法确定花岗岩中不同细观组分之间的灰度分界阈值[16]。裂隙-黑云母、黑云母-长石、长石-石英的灰度分界阈值分别为59、135、203。根据这些分界阈值，得到岩石中不同细观组分的具体类型与实际分布。

3.2 不同组分的分形特征

3.2.1黑云母的分形特征

由图4可知，在变形阶段，黑云母的简单分形维数变化不大，广义分形维数变化较大，Dmin由2.541增大到2.597，Dmax由2.026增大到2.034，A和B也变化较大，A由0.360增大到0.600，B由0.963增大到1.059；在破坏阶段，裂隙较少时，黑云母简单分形维数突然增大、由1.284增到1.331，广义分形维数发生突降，Dmin由2.597降到2.533，Dmax由2.034降到2.008，A和B突然降低，A由0.600突降到0.393，B由1.059突降到1.000；在破坏阶段，裂隙较多时，黑云母的简单分形维数变化较大、由1.336减小到1.321，Dmin由2.512增大到2.554，Dmax由2.017增大到2.016，A和B变化都较大，A由0.420增大到0.472，B由0.961增大到1.026。

图4 黑云母分形维数随时间的变化Fig.4 Variations of fractal dimensions with time of biotite

3.2.2长石的分形特征

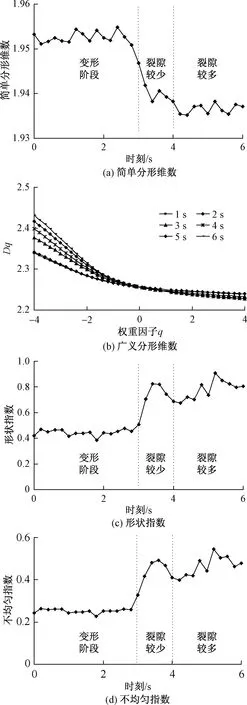
图5 长石分形维数随时间的变化Fig.5 Variations of fractal dimensions with time of feldspar

由图5可知，在变形阶段，长石的简单分形维数变化不大，广义分形维数、A和B变化也较平稳；在破坏阶段，裂隙较少时，简单分形维数突然减小、由1.954突降到1.938，Dmin突然增大、由2.343增大到2.441，Dmax突然降低、由2.239减小到2.229，A和B都突然增加、A由0.454增大到0.823、B由0.258增大到0.482；在破坏阶段，裂隙较多时，长石简单分形维数变化不大，Dmax变化不大，Dmin变化较大、由2.398增大到2.431，A和B的变化也较大，A由0.688增大0.805，B由0.409增大到0.479。

3.2.3石英的分形特征

图6 石英分形维数随时间的变化Fig.6 Variations of fractal dimensions with time of quartz

由图6可知，在变形阶段，石英简单分形维数变化较大、由1.786降到1.777，广义分形维数变化较大，Dmin由2.637减到2.626 6，Dmax由2.139降到2.130，A和B变化不大；在破坏阶段，裂隙较少时，简单分形维数突然增大、由1.777突增到1.790，广义分形维数突然增大，Dmin由2.626增到2.666，Dmax由2.130增到2.136，A和B都突然增加，A由0.714增到0.839，B由0.900增到0.979；在破坏阶段，裂隙较多时，简单分形维数稍有变化、由1.791增加到1.795，广义分形维数变化较大，Dmin由2.700减小到2.666，Dmax由2.136增大到2.141，A由0.908减小到0.863，B由1.026减小到0.965。

3.3 不同组分分形特征的比较

不同组分、不同分形维数的不同变化模式，反映了不同组分区域的面积大小、复杂程度、不规则程度、不均匀程度的不同变化情况，可以将前述不同分形维数绘于同一张图上来对比分析岩石变形破坏过程中不同细观组分分形维数的变化特点。

图7为不同细观组分简单分形维数变化的比较。由图7可知，在变形阶段和破坏阶段裂隙较多时，三种组分的简单分形维数都变化不大；破坏阶段裂隙较少时，石英简单分形维数变化不大，黑云母简单分形维数增大，长石简单分形维数减小，简单分形维数变化大小顺序是：黑云母>长石>石英。

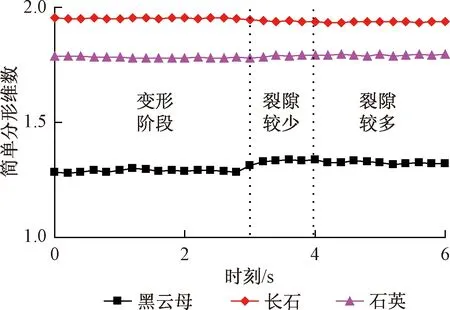
图7 不同细观组分简单分形维数变化的对比Fig.7 Variations of simple fractal dimensions with time in various meso-compositions

图8为不同细观组分广义分形维数最大值Dmax和最小值Dmin的比较。由图8可知，在变形阶段，三种组分Dmax变化都不大，长石Dmin的变化不大，黑云母和石英Dmin的变化较大，Dmin变化大小顺序为黑云母>石英>长石，变形主要发生在黑云母和石英小面积区域；在破坏阶段、裂隙较少时，三种组分广义分形维数变化都较大，石英Dmax变化相对较小，黑云母和长石Dmax减小，长石和石英Dmin突然增大而黑云母Dmin突然减小；在破坏阶段、裂隙较多时，三种组分Dmax变化不大、Dmin变化较大，变形主要发生在面积较小的区域。

图8 不同细观组分广义分形维数变化的对比Fig.8 Variations of generlized fractal dimensions with time in various meso-compositions

图9为不同细观组分形状指数变化的比较，图10为不同细观组分不均匀指数变化的比较。

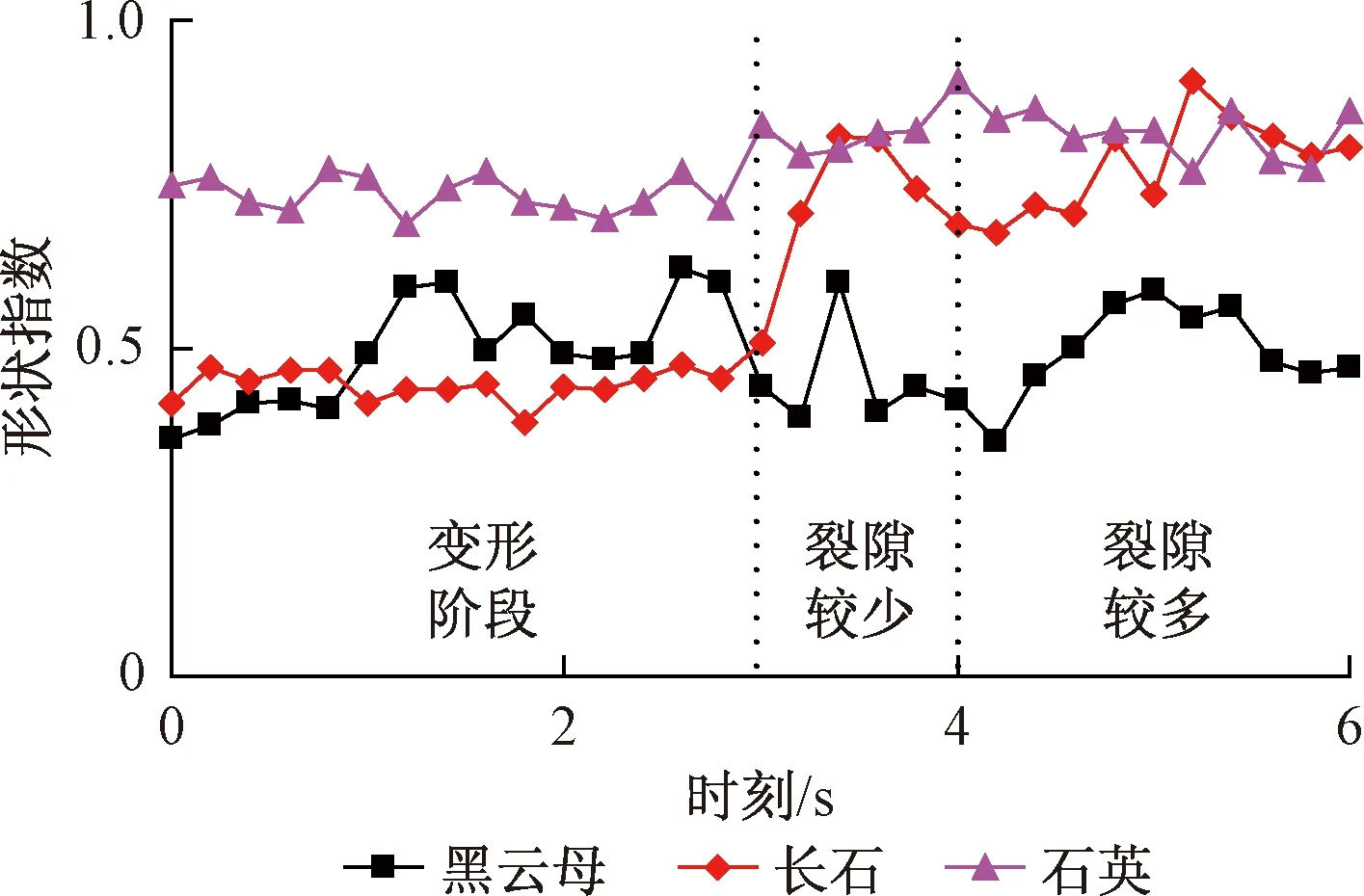
图9 不同细观组分形状指数变化的对比Fig.9 Variations of shape index with time in various meso-compositions

图10 不同细观组分不均匀指数变化的对比Fig.10 Variations of non-uniformity index with time in various meso-compositions

由图9和图10可知，对多重分形谱参数(形状指数和不均匀指数)来说，在变形阶段，三种组分的形状指数变化都较大，长石和石英不均匀指数变化不大而黑云母不均匀指数变化较大，可能是黑云母面积很小且分布较分散、受外力影响最大；在破坏阶段，裂隙较少时，黑云母不均匀指数和形状指数突然减小，而长石和石英的不均匀指数和形状指数却突然增大；在破坏阶段，裂隙较多时，三种组分的形状指数变化都较大，而三种组分的不均匀指数变化相对较小。

4 结 论

根据花岗岩的单轴压缩试验结果和试验过程中拍摄的试验视频，使用数字图像处理技术研究了岩石变形破坏过程中不同细观组分简单分形维数、广义分形维数、多重分形维数的变化特征，得到如下结论：

(1)在变形阶段，黑云母和长石的简单分形维数变化不大，石英简单分形维数变化较大，三种组分广义分形维数最大值变化不大，广义分形维数最小值变化大小顺序为黑云母>石英>长石，三种组分的形状指数变化较大，长石和石英不均匀指数变化不大而黑云母不均匀指数变化较大；

(2)在破坏阶段、裂隙较少时，黑云母和石英的简单分形维数突然增大、而长石简单分形维数突然减小，石英广义分形维数最大值变化不大、黑云母和长石广义分形维数最大值减小，长石和石英广义分形维数最小值突然增大、而黑云母广义分形维数最小值突然减小，黑云母不均匀指数和形状指数均突然减小、而长石和石英的不均匀指数和形状指数均突然增大；

(3)在破坏阶段、裂隙较多时，不同组分的简单分形维数变化不大，广义分形维数最大值变化不大、而广义分形维数最小值变化较大，三种组分形状指数变化较大、而不均匀指数变化较小。