钢筋混凝土框架结构构件地震损伤评估

贺文洲，王国新

（1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024;2.大连理工大学 建筑工程学部水利工程学院 工程抗震研究所，辽宁 大连 116024）

0 引言

地震是一种危害极大的突发性自然灾害，限于科学技术等方面的限制，很难对地震发生的时间及地点进行准确的预知。当前国内外的防震减灾工作主要体现在震前建筑物的抗震结构设计及震后的安全评估方面。考虑到经济方面的因素，在结构抗震设计中往往允许结构在中等或强地震下有一定程度的损伤、甚至较为严重破坏但不至倒塌，因此，对结构开展震后的安全性评估工作就变得尤为重要。

结构的安全性估价即结构的损伤评估可分为定性分析与定量分析两大类：定性分析可参考《建筑物抗震鉴定标准》、《建筑物安全鉴定》[1-2]等文献。定量分析是考虑地震时结构或构件的位移、耗能、延性等因素中的一项或多项组合，确定一个介于0～1之间的损伤指数，以此来表征结构或构件的损伤情况，此方法较定性分析工作量大，但分析结果更准确更具体，评估效果更为准确。

本文以开源程序OpenSEES为平台建立一个6层框架结构的数值模型进行非线性时程分析，从构件层次上确定每根构件的损伤指数。为验证模型的正确性，选取文献[3]中的RC柱实验数据建立OpenSEES模型，将模拟数据与实验数据对比来验证模型的正确性。

1 双参数损伤模型

结构双参数损伤模型选用退化、变形、能量三类参数中的两类进行线性组合，其中应用最广泛的综合模型是Park和Ang提出的同时考虑最大位移和累计滞回耗能的Park-Ang双参数损伤模型[4]，如下式：

式中，D为损伤指数；mδ为构件在地震作用下的实际最大变形；uδ为在单调荷载下的极限变形；为地震作用下构件的累计滞回耗能；β为构件的耗能系数。当 D≤0时构件无损伤，当 D=1时构件完全破坏。

之后，各国学者[5-9]以Park-Ang双参数损伤模型为理论基础进行了大量研究，提出了适用于不同结构的损伤模型。本文选用吕大刚和王光远[10]提出的综合损伤模型：

式中，yδ为构件的屈服变形；EH为累积滞回耗能。其它参数意义同式（1）。

2 损伤模型参数计算

在计算构件的损伤指数时，一个很重要的环节是计算模型中所需参数:屈服荷载Fy、屈服变形yδ、最大变形mδ、极限变形uδ、累计滞回耗能EH以及耗能系数β。这里的荷载与变形是广义的，可以是构件的剪力与水平位移，也可以是截面的弯矩与曲率。对于梁构件，本文选用端部截面的弯矩-曲率计算损伤指数，对于柱构件，分别选用力-位移和弯矩-曲率计算构件的损伤指数，并比较两者的优劣。

2.1 最大变形与累计滞回耗能

最大变形mδ可由时程计算中直接给出，对于累计滞回耗能，本文通过下式进行计算：

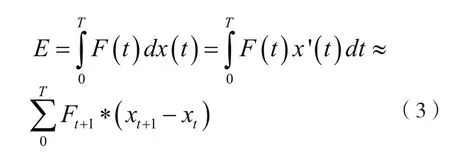
2.2 屈服荷载、屈服变形和极限变形

当选取力-位移计算柱构件的损伤指数时，借助OpenSEES绘制每根柱的滞回曲线，并以此确定构件骨架曲线，通过三折线等效线性化，取骨架曲线上升段75%峰值荷载点为屈服点，取下降段85%峰值荷载点为极限点。

当选取弯矩-曲率计算梁柱构件的损伤指数时，借助截面分析软件X-TRACT对截面进行分析，得到截面的屈服弯矩、屈服曲率、极限曲率。

2.3 耗能系数β

Park等人在大量钢筋混凝土梁、柱实验的基础上，给出了改进的β的经验计算公式：

式中，λ为构件的剪跨比；n0为构件轴压比；ρ为全部纵筋的配筋率；wρ为体积配箍率；kρ为归一化的配筋率，计算公式如下：

式中， fy为受拉钢筋的屈服强度； fc为混凝土轴心受压强度。

3 钢筋混凝土柱数值模拟

为验证本文所计算的参数及所建数值模型的正确性，建立文献[3]中试验柱的OpenSEES模型，将模拟结果与实验结果进行对比验证模型的正确性。模拟结果和实验结果对比如图1所示。

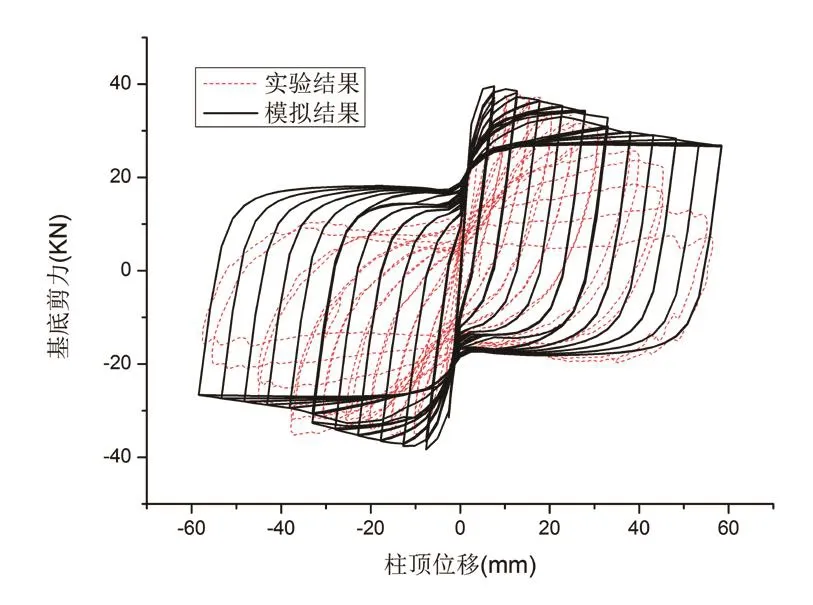
图1 模拟结果对比图Fig.1 Comparison of simulation result

由对比结果可知，按照本文所述参数计算方法建立模型，对钢筋混凝土柱的屈服位移和屈服荷载拟合效果较好，并且可以很好的模拟梁柱构件在地震等往复作用下的反应。

4 框架地震损伤计算

4.1 材料参数

本文使用结构设计软件PKPM设计了一栋六层钢筋混凝土框架，场地类别为二类，抗震设防烈度为7度（设计地震加速度为0.15g），不考虑风荷载，由PKPM计算的结构自振周期为0.81s。对底层柱进行加强设计，考虑到梁端负弯矩的影响增大了端部配筋率，本文取中间一榀框架进行计算分析。结构立面、构件编号及截面配筋信息如图2所示。

图2 结构立面、构件编号及截面配筋图（单位：mm）Fig.2 Vertical section of structure,components,number and section reinforcement diagram

结构混凝土等级为C40，纵向钢筋及箍筋均选用HRB400钢筋。材料基本参数参考规范[11]。本文参考文献[12],选取Concrete01模拟混凝土材料，Seel02模拟钢筋材料，选用mander[13]本构模型考虑箍筋对核心区混凝土的加强作用。所需各参数计算结果列于表1和表2中。

表1 OpenSEES混凝土参数

表2 OpenSEES钢筋参数

建立OpenSEES模型时，材料各参数按照表1、表2取用，经计算，OpenSEES程序计算得到框架基本周期为0.78s，与PKPM计算结果非常接近，证明了模型的正确性。

4.2 损伤模型参数

构件的屈服荷载、屈服变形、极限变形（下文简称性能点）可由经验公式求得，但经验公式是在既有实验的基础上总结而出，具有一定的离散性，为使本文分析结果更准确，本文对结构每根构件单独建模，求得每根构件的性能点。

4.2.1 剪力-位移模型参数

当选取剪力-位移计算柱构件的性能点时，建立每根柱的OpenSEES数值模型，对其进行低周往复分析和推覆分析，绘制出构件的骨架曲线，篇幅所限，本文仅列出部分构件的滞回曲线及推覆曲线。如图3所示。

对以上各图进行分析总结出如下规律：

（1）在构件尺寸配筋相同的情况下，轴向压力越大，屈服荷载随之增大，这是由于轴向力增加了构件的附加刚度，但降低了构件延性，故结构在地震等往复荷载作用下，结构较低层往往最先破坏；

（2）将滞回曲线每次循环位移的峰值点连成曲线即为构件的骨架曲线，对构件进行单调加载直至构件破坏所绘曲线为pushover曲线，由图中可知，OpenSEES软件分析所得骨架曲线与pushover曲线几乎完全重合，本文将pushover曲线作为构件的骨架曲线；

(3)在轴向压力较小时，曲线下降段不明显，如上图中第五层中柱，将导致构件损伤指数结算结果偏小。

根据上文2.2章节，取骨架曲线上升段75%峰值荷载点为屈服点，取下降段85%峰值荷载点为极限点。柱构件损伤模型参数列于表3。

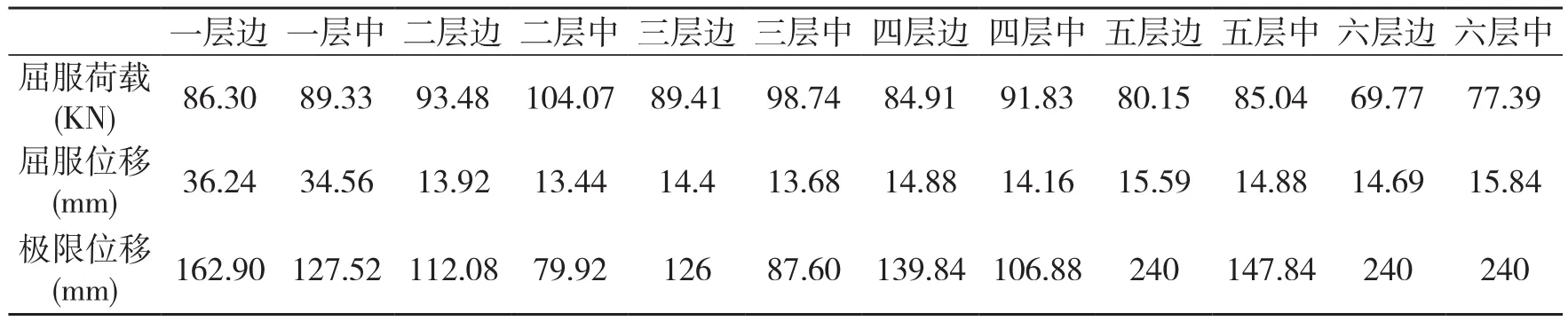
表3 柱构件力-位移参数

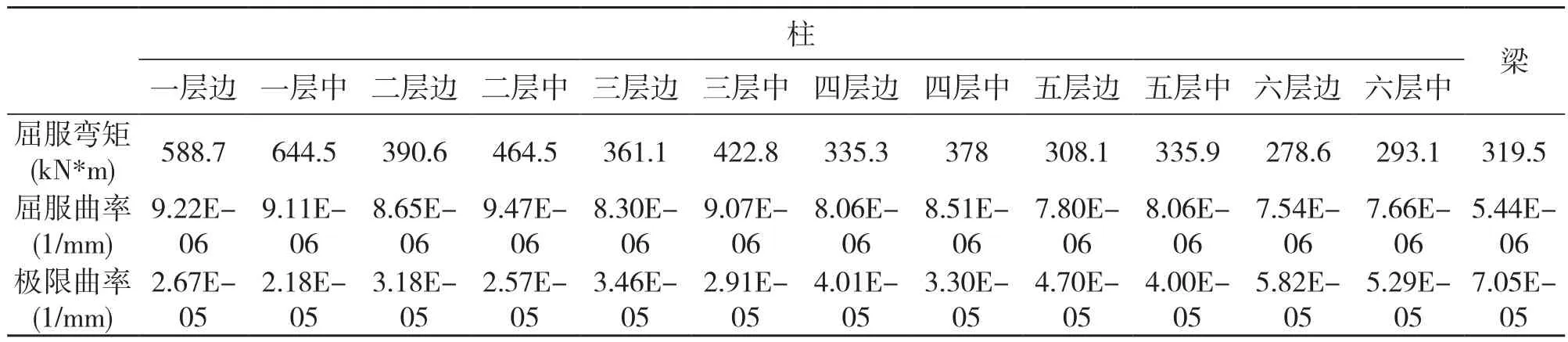
表4 柱构件弯矩-曲率参数

4.2.2 弯矩-曲率模型参数

本文借助截面分析软件X-TRACT求得各构件截面的弯矩-曲率变化关系，计算结果列于表4。建模时各材料参数同表1、表2。

4.2.3 耗能系数

由式（2）-（3）计算各构件耗能系数列于表5。

表5 各构件耗能系数

4.2.4 地震波输入

本文选取两条经典地震波EL CENTRO和TRAFT分别对结构进行激励。文本结构设计加速度为0.15g，为得到大震作用下结构的反应，将地震波峰值加速调整为0.3g。

由上文可知，由于OpenSEES软件自身局限，当上部轴向荷载较小时，可能引起滞回曲线下降过缓，则计算的损伤指标将偏小。而由X-TRACT截面分析软件对截面进行弯矩-曲率分析时，则不会出现这种情况。综上所述，本文选取构件截面的弯矩-曲率计算构件的损伤指标。

由以往地震灾害情况可知，框架结构在地震作用下破坏最严重的一般为结构底层，对此，本文对底层柱构件进行了加强。为对比分析底层柱构件加强与不加强对结构的影响，本文另建立一底层不加强的框架模型（其它构件与原结构完全相同），并输入同样的地震时程。损伤指数与破坏等级的对应关系参考文献[10]。两个结构在地震荷载下各个构件的损伤指数与破坏等级列于表6、表7。

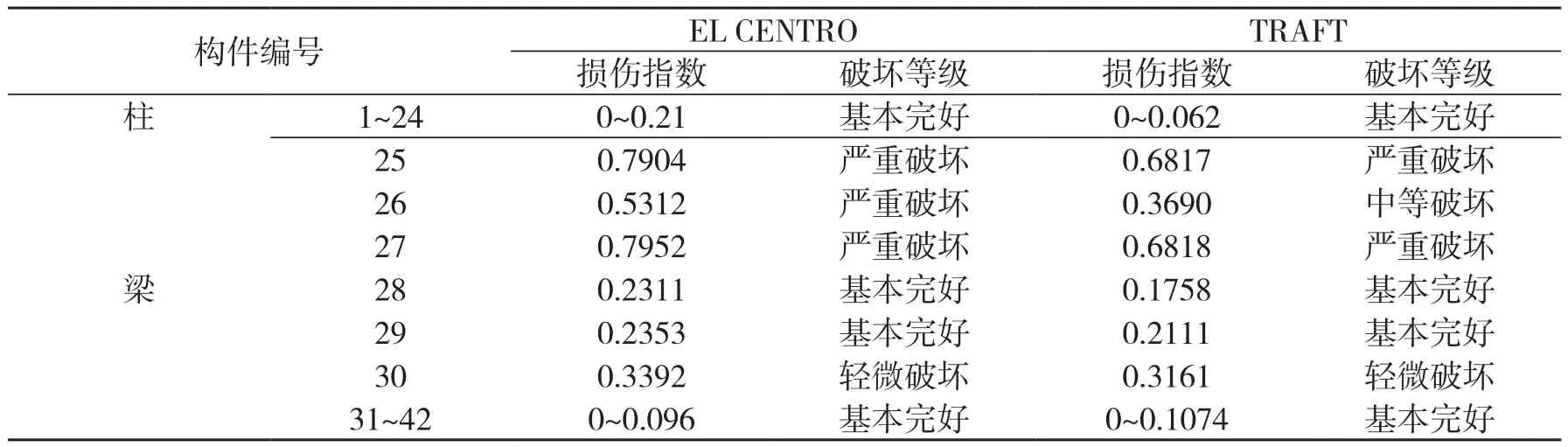
表6 底层加强框架地震作用下各构件损伤指数

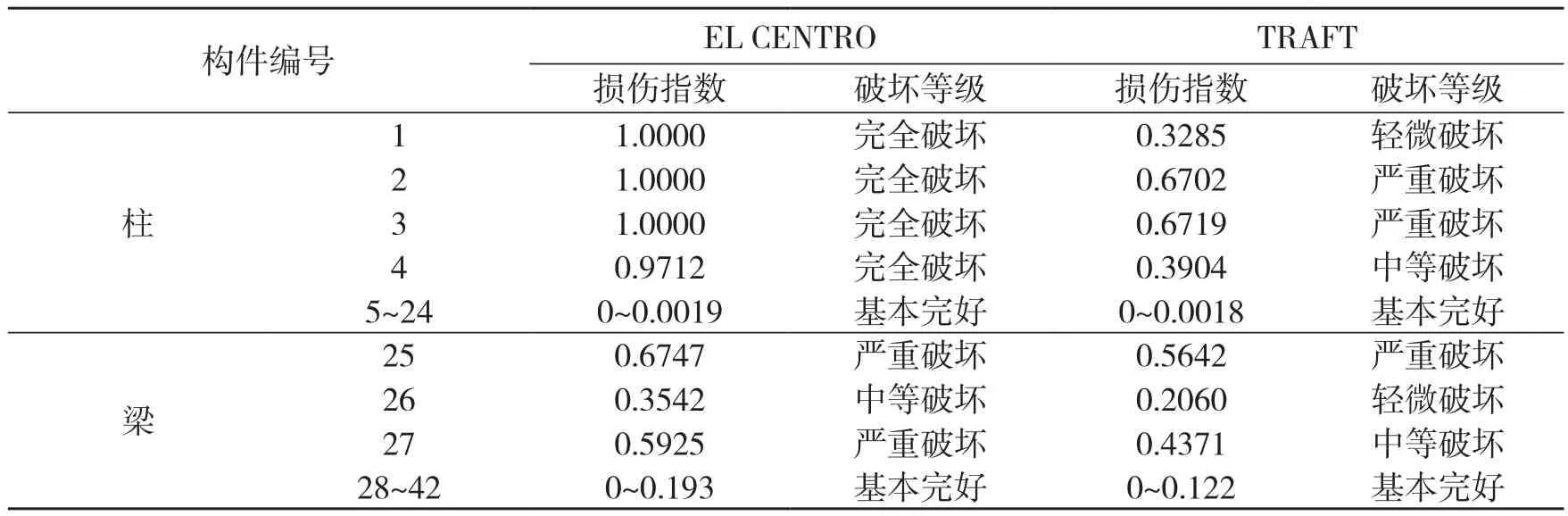
表7 底层不加强框架地震作用下各构件损伤指数

对表6、表7中的损伤指数进行对比分析可知：

（1）对于柱构件，底层中柱的损伤指数最大，与现实地震作用下底层柱破坏严重现象相符。对于梁，一层边梁的损伤指数最大，破坏较为严重，故结构底层为框架结构的薄弱层。

（2）当底层框架柱不进行加强设计时，由表7可知，底层柱破坏严重，在EL CENTRO地震作用下，底层柱已完全破坏，一层边梁有不可修复的严重破坏，中柱有中等破坏；在TRAFT地震作用下，底层中柱有不可修复的严重破坏，边柱有中等破坏，一层边梁有中等破坏，中部梁有轻微破坏。底层柱与一层梁为框架结构地震作用下的最薄弱部位。

（3）当底层框架柱进行加强设计时，由表6可知，底层柱破坏大为减轻，构件基本完好，一层梁有不可修复的严重破坏，结构整体不会出现倒塌，符合抗震设防三水准中的“大震不倒”原则；可以预见，在地震继续加强时，一层梁将先于柱破坏，符合“强柱弱梁”的设计原则。

（4）地震加速度峰值相同时，不同的时间历程会对结构产生不同的影响，结构在EL CENTRO和TRAFT波作用下，截面最大曲率非常接近，但滞回耗能相差较大，故本文所选用的同时考虑变形和耗能的双参数损伤模型更为合理。

5 结论

本文选用同时考虑变形和耗能的双参数损伤模型计算结构在地震作用下的损伤程度。经对比，以截面的弯矩-曲率为基础计算损伤指标更为合理。

以OpenSEES软件为平台建立一个六层框架数值模型并进行非线性时程分析，结论如下：

（1）结构底层为结构的薄弱层，地震作用下往往最先破坏。为使结构在大震作用下不致倒塌，应对底层柱进行加强设计。

（2）当底层柱不进行加强时，底层柱破坏最严重，在大震作用下有倒塌的危险；当对底层柱进行加强设计时，柱的破坏大为减轻，一层梁将先于柱破坏，符合“强柱弱梁”原则，且结构在大震作用下未倒塌，符合“大震不倒”的设防原则。

（3）即使峰值加速度相同，不同的地震动作用下亦会产生不同的结构响应，因此，在判别结构的损伤程度时应根据不同的地震动特点分别得出具有针对性的评价结果。