锚护网络结构多目标进化优化设计方法研究
李 玉
(山西省煤炭建设监理有限公司,山西 太原 030012)
引 言
煤矿开采是我国重要的工业经济支柱产业,对能源经济发展影响深远,在未来很长时期内还将占据主力地位。煤矿开采巷道采用锚杆支护网络,其支护结构的优良直接关系到巷道的稳定性,采用锚杆数量越大,巷道支护越稳定,但与之而来的是支护时间和成本的增长,这对煤矿开采的高效率形成了牵制[1-2]。相反,锚杆数量少虽然可以减少支护成本,但其支护稳定性可能会受到影响,出现冒顶、片帮和坍塌事故更是损失严重[3-4]。所以,对于煤矿巷道的支护应选择合理的巷道支护结构,在保证安全的基础上尽可能节省成本。本文采用多目标进化优化设计方法对巷道锚杆支护进行了研究,围绕支护质量、成本和时间进行优化分析,以实现巷道锚护的最优方案选取。
1 锚护网络构架多目标数学模型
1.1 决策变量
在锚杆支护网络设计过程中,要尽可能地考虑安全、成本和效率3方面问题,本文将以支护质量、成本、和时间3个目标为函数来进行分析,需要建立三目标优化模型,并通过数学算法进行模型分析[5]。支护质量和支护网络关系复杂,因此,将围岩变形量作为分析支护质量的参考量,其包含顶底板和帮部移近量,创建模型对支护质量进行反映[6]。综合考虑煤矿巷道支护时间状况,以锚杆配合锚索组合支护为研究,将支护影响要素作为决策变量,主要包含支护核心参数,设决策变量为x={x1,x2,…,x11},其中参数分别为锚杆直径、锚杆长度、锚索布置形式、锚索直径、锚索和锚杆的排距比值、锚杆顶部间距、锚杆的排距、锚杆帮部间距、锚索长度、锚杆预紧力和锚索预紧力,其中,锚索布置形式包括每排布置1根、奇数排2根偶数排1根、每排2根锚索,分别用数字1、2、3代表;排距比值可选0,1,2,3,4,5,其中,0表示没有锚索支护。
1.2 目标函数
支护质量是首先考虑的目标之一,其体现了围岩在锚护网络支护下的可靠程度,可依靠围岩变形情况来反映支护质量,对顶底板和两帮的移近量进行测量来表示围岩的变形情况,因其具有高度非线性关系,所以采用代理模型评价锚护方案与支护质量的联系。因为锚杆和锚索大量参数为离散数据,所以通过正交实验得出方案来确保数据典型,运用监督学习方法来识别支护方案与顶底板、两帮移近量的关系,设计顶底板和两帮支护质量代理模型分别为RF(x)和TS(x)。
支护成本是在维持支护稳定的基础上主要研究的方向,影响了开采的经济性,锚杆、锚索的材料及质量都是支护成本的主要因素。因为支护所用锚杆及锚索的材料相对比较单一,所以支护成本是通过支护所需材料的质量来进行衡量,支护成本可用第187页式(1)计算。
(1)
式中:锚杆价格为cg,元/kg,锚索价格为cs,元/kg,两者密度分别为ρg与ρs,顶板和两帮布置的锚杆宽度为kd和kc,mm,巷道长L,m。
支护时间体现了开采的总体速度,对生产效益影响重大,支护时间受支护材料的总体积影响。可以通过公式(2)计算支护时间。
(2)
式中:锚杆支护时间为tg,min/m3,锚索支护时间为,ts,min/m3。
根据巷道工程要求,确定目标函数极限值作为约束条件,设计锚护网络多目标优化模型。函数公式为式(3)。
minF(x)=(TS(x),RF(x),C(x),T(x))
(3)
选择随机100组支护成本与时间的数据联系进行分析,如图1所示。

图1 支护时间与支护成本关系曲线
由图1可以看出,支护时间和成本拟合出线性关系,C(x)=aT(x)+b,由此,可将支护时间的求解简化为支护成本的求解,目标函数可简化为式(4)。
minF(x)=(TS(x),RF(x),C(x))
(4)
2 实例分析
本文以古交燎原煤矿8101工作面为研究对象,运用FLAC3D以及MATLAB软件进行计算,使用设计方法为非支配排序的多目标遗传算法,种群规模为200,最大迭代次数为300,交叉指数20,变异指数20,两者概率为0.8和0.2。优化计算后结果如图2所示。
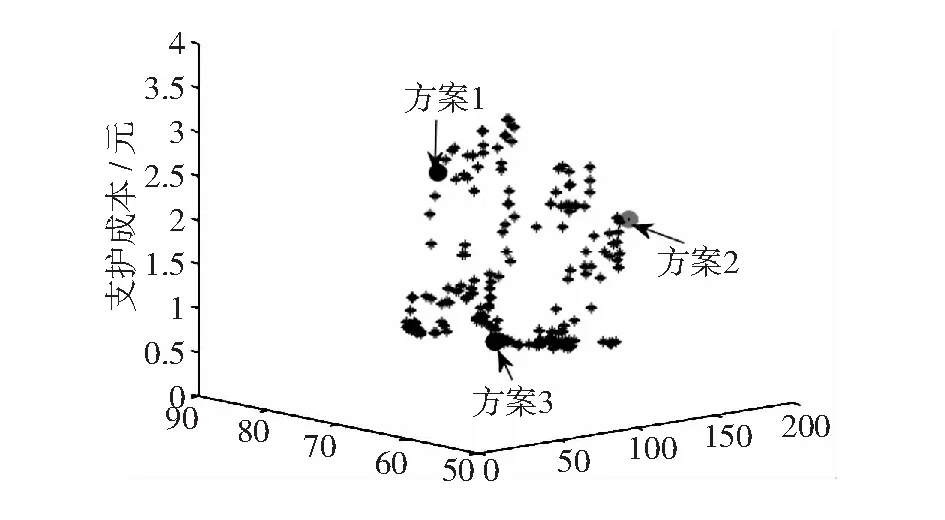
图2 锚护网络结构优化方案
由图2可以看出,优化后方案并不仅有1种,存在3种方案,分别是:最小帮部位移量、最小顶底板位移量和最小支护成本。参考其他文献最优方案[4],计为第4种方案,分别对4个方案进行结构分析,得出锚护网络断面分布如第188页图3所示,顶底板位移量和两帮位移量如第188页图4、图5所示。
由以上分析结果可以得出,巷道顶底板和帮部移近量低于已经存在的第4种最优方案,说明支护质量优于现有方案,成本最优的方案支护质量也要高于现存支护方案,所以,采用这种多目标遗传算法得到的3种最优方案均能够满足设计的要求,实现更多选择的优化设计方案。
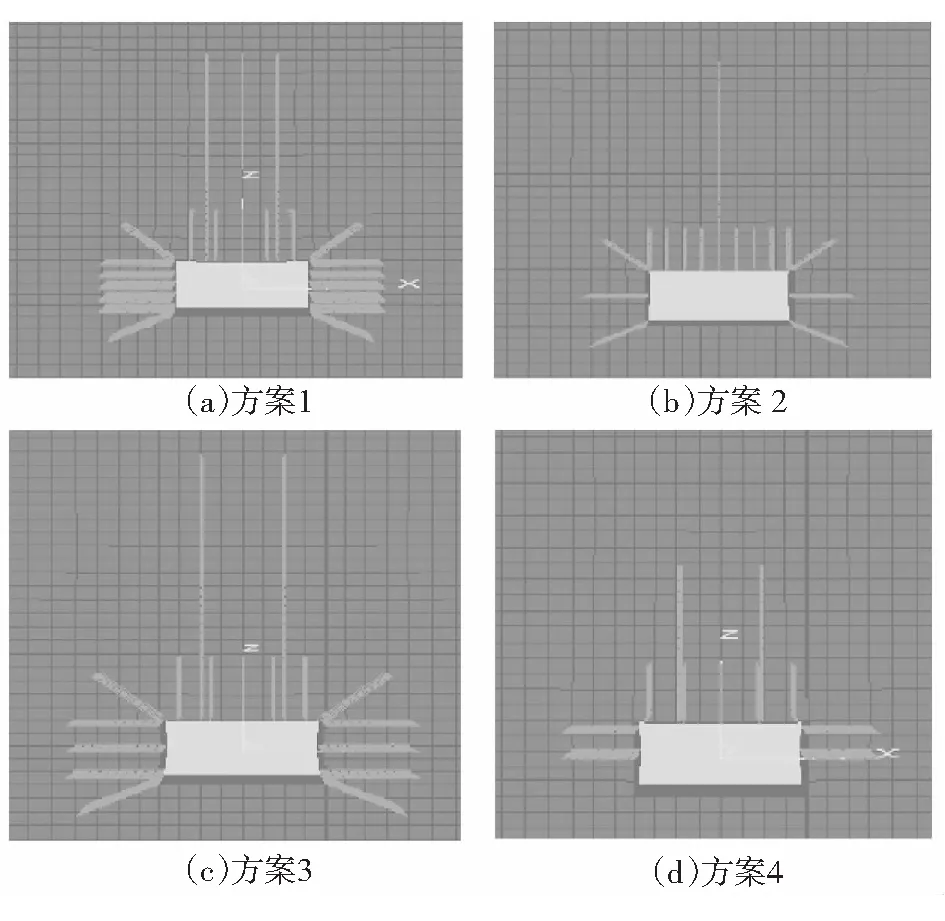
图3 锚护网络断面分布
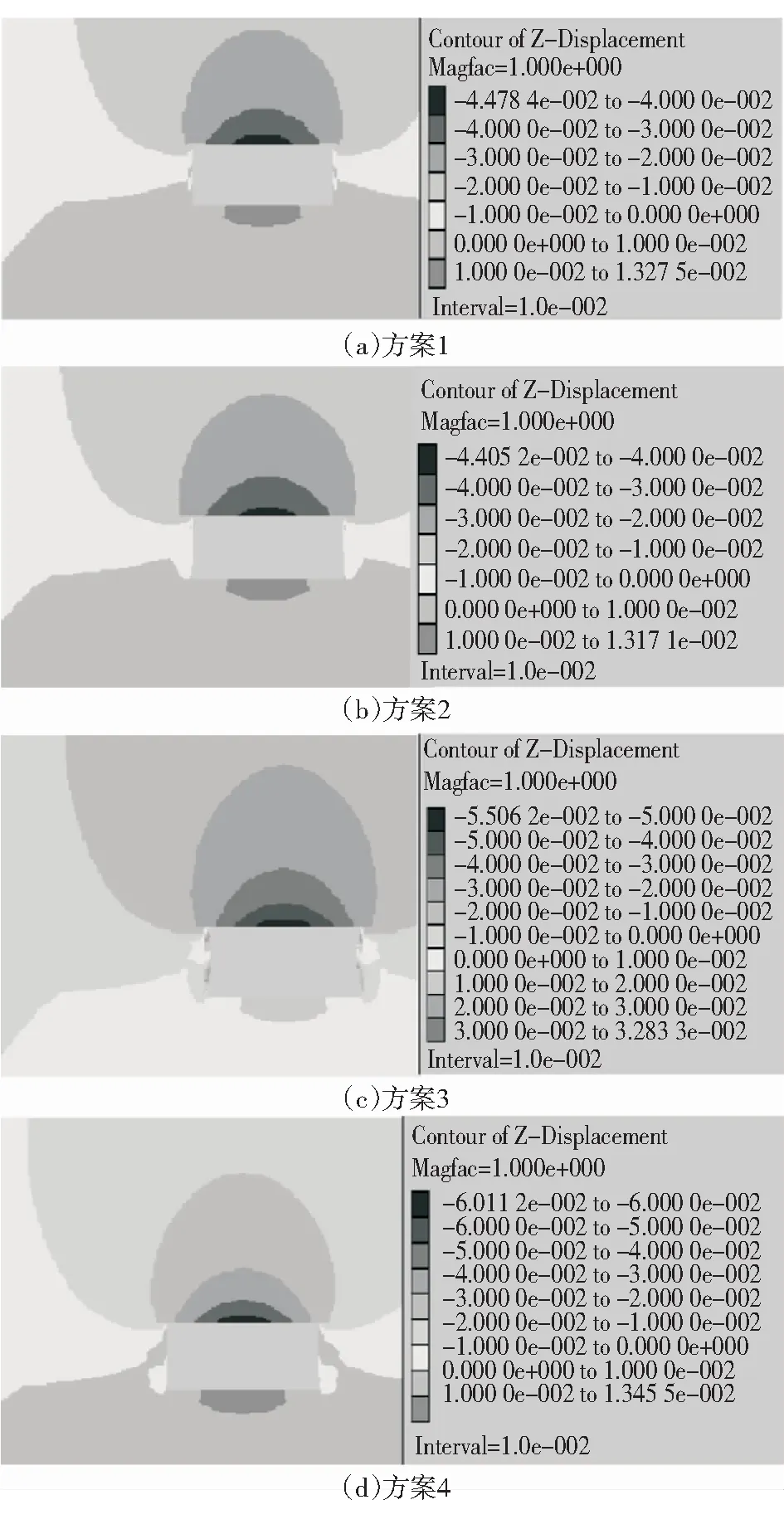
图4 巷道顶板和底板位移量
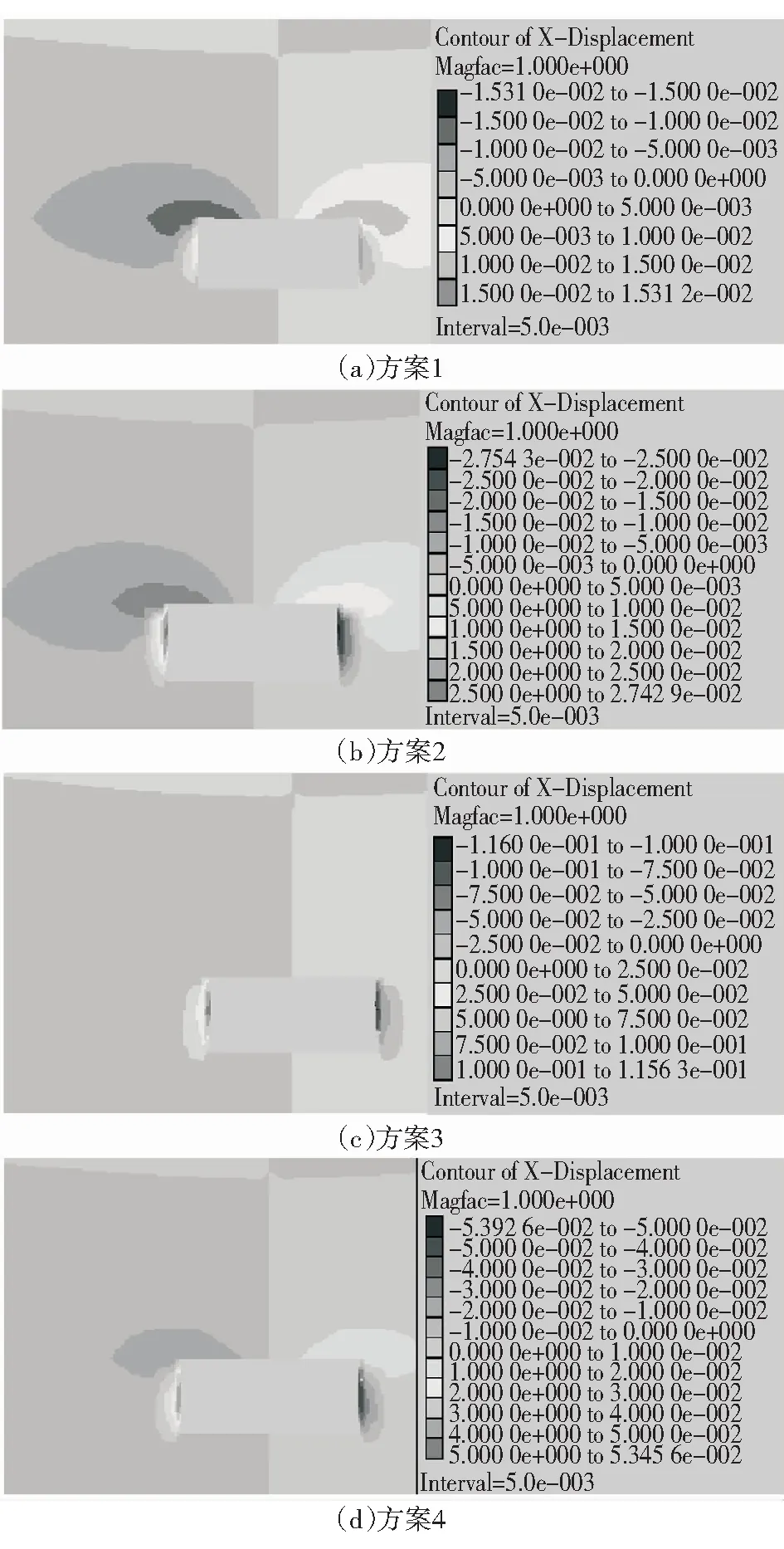
图5 巷道两帮位移量
3 结论
本文针对煤矿巷道支护过程中存在的锚护网络结构复杂等问题,考虑安全、经济和效率等要素的影响,对锚护网络的支护质量、成本和时间3个目标建立函数模型,运用非支配排序的多目标遗传算法进行求解,得出了针对顶底板移近量、两帮移近量和支护成本的3种最优方案,并与已有优化方案进行模拟对比,结果证明,此方法得出的优化结果效果更好,为锚护网络优化研究提供了理论依据。

