±800 kV特高压直流输电线路地线选型

朱 罡，杨禹太，单 军，王世龙，杨永宽

（1.中国能源建设集团云南省电力设计院有限公司，云南 昆明 650051；2.国网山东省电力公司威海供电公司，山东 威海 264200；3.山东送变电工程有限公司，山东 济南 250118；4.国网山东省电力公司建设公司，山东 济南 250001）

0 引言

一般架空输电线路地线选型主要按热稳定要求、机械强度要求、导地线不均匀覆冰时静态接近的要求及导线脱冰跳跃和覆冰舞动时动态接近的要求（重冰区）、与导线配合取得合理的地线支架高度及防雷保护角等几个因素选择。但对于特高压直流输电线路，因地线感应电荷大，不考虑离子流影响，地线表面电场强度也很大，超过电晕起始电场时同导线一样会产生电晕损失、无线电干扰以及可听噪声，必须给予限制，在《±800 kV直流架空输电线路设计规范》中5.0.7款中，规定地线表面电场强度不宜大于18 kV/cm［1］。计算地线表面场强时可参考导线表面场强计算的方法。通过解析法、有限元法分别计算不同直径的地线表面场强，得出工程地线需满足的最小截面积。

1 解析法计算地线表面电场强度

1.1 输电线路简化模型

为了便于分析计算，假定如下条件：导线未发生电晕、地面十分平坦、导地线十分水平、分裂导线计算中采用等值单导线代替，并将输电线路视为无限长直导线，地面为良导体，空间场强转化为二维场计算，简化模型如图1所示。

图1 简化模型

1.2 计算方法

采用镜像法进行计算［2］。

分裂导线的等效直径

式中：D为通过n根次导线中心的圆周直径，mm；n为次导线的分裂根数；d为次导线的直径，mm。

导线上电荷Q采用麦克斯韦电位系数法计算

式中：α为电位系数矩阵，包含自电位系数和互电位系数。

自电位系数

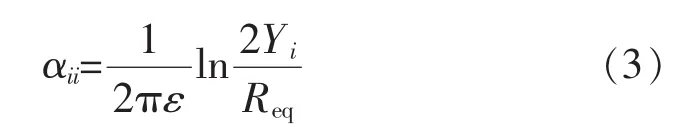
互电位系数

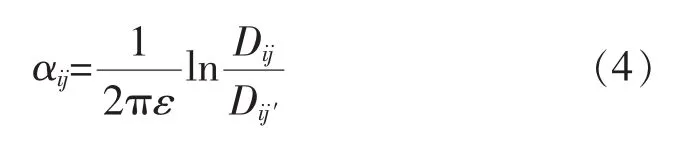
导线平均表面电场强度

式中：g为电场强度，kV/cm；Q为等效电荷，C/m。

导线最大表面电场强度

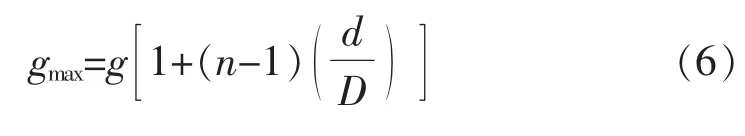
2 有限元法计算地线表面电场强度

输电线路周围电场按静电场计算。在静电场中，根据高斯定律的微分形式，电通量定义以及梯度关系可知［3］：

由式（7）～（9）可得在均匀介质中的泊松方程和拉普拉斯方程（空间电荷密度为零）：

利用有限元数值方法可以求解拉普拉斯方程，即给定一个区域，并指定区域的边界条件，然后进行网格剖分，计算得到区域内电场强度。

3 不同截面地线的表面电场强度计算

3.1 不同截面时地线表面电场强度

±800 kV双极单回路水平排列的架空线如图1所示。根据±800 kV山西—江苏特高压直流输电线路工程情况，线路典型参数为：导线规格6×JL1/G3A—1250/70，导线直径 47.35mm，分裂间距为 500mm，导地线对地距离平均高度分别取30m、45m。

有限元计算时，计算区域长度取80m，宽度取65m。矩形上边按第一类边界条件设置为零，矩形侧面两条边按第二类边界条件设置，矩形底边设置为零；不考虑离子流影响，即空间电荷密度取零。

计算80m×65m矩形区域内，极间距20m时的电场强度分布如图2～5所示。图中实线表示场强等值线。

由图形对比分析可知，特高压输电线路地线表面电场强度已经接近导线表面电场强度。随着地线截面（直径）的增大，地线表面电场强度降低，由此可选择满足限值要求的地线截面。120mm2地线已经超过18 kV/cm规范值，150mm2地线截面则满足小于18 kV/cm的要求。

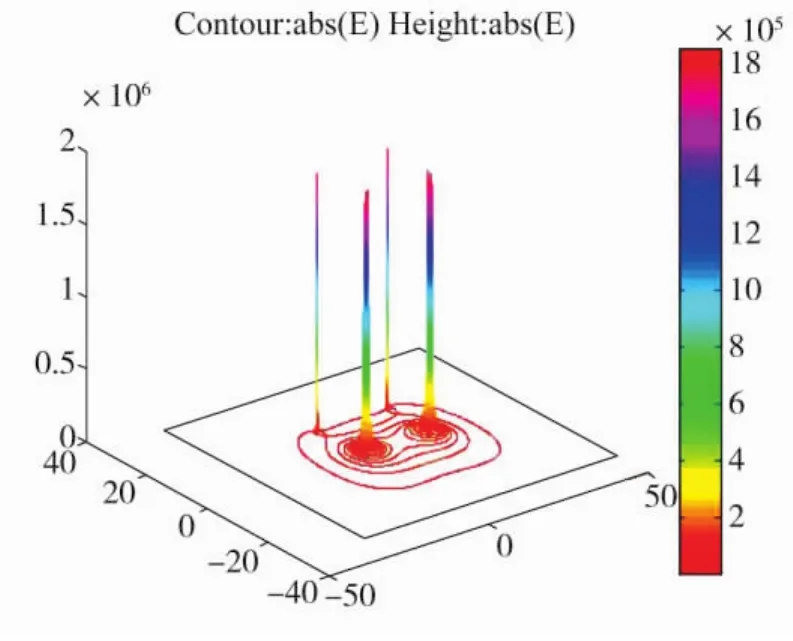
图2 120mm2地线时的场强空间分布

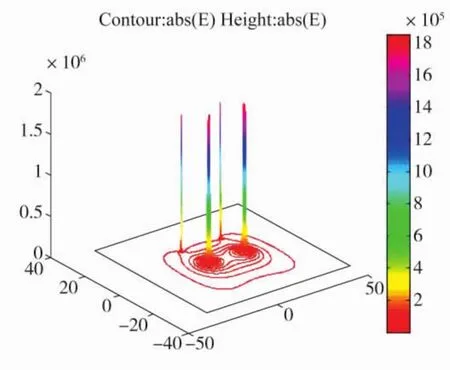
图3 150mm2地线时的场强空间分布

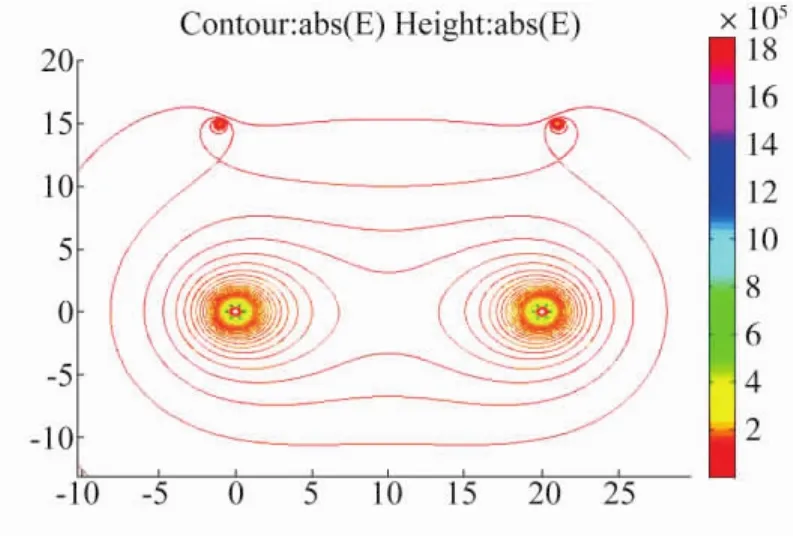
图4 120mm2地线时的场强平面分布

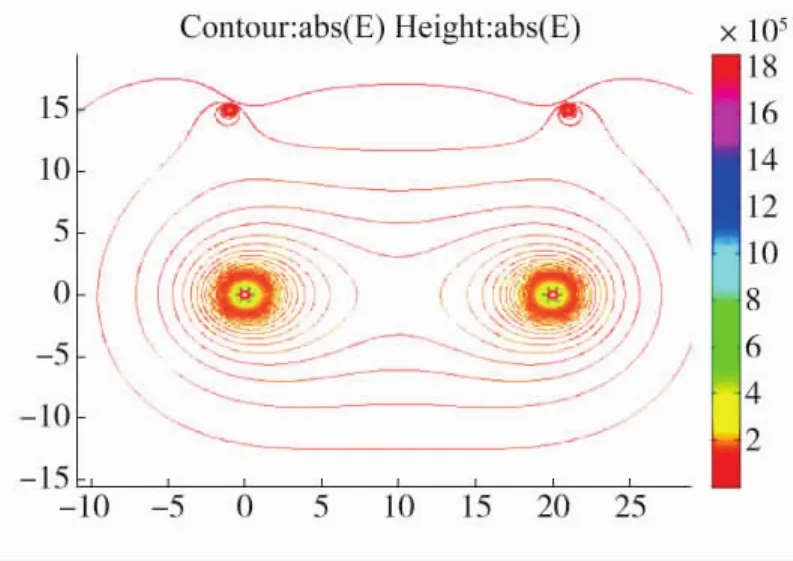
图5 150mm2地线时的场强平面分布

3.2 不同极间距时地线表面场强

其他因素不变，计算不同极间距时的地线表面电场强度如表1所示。

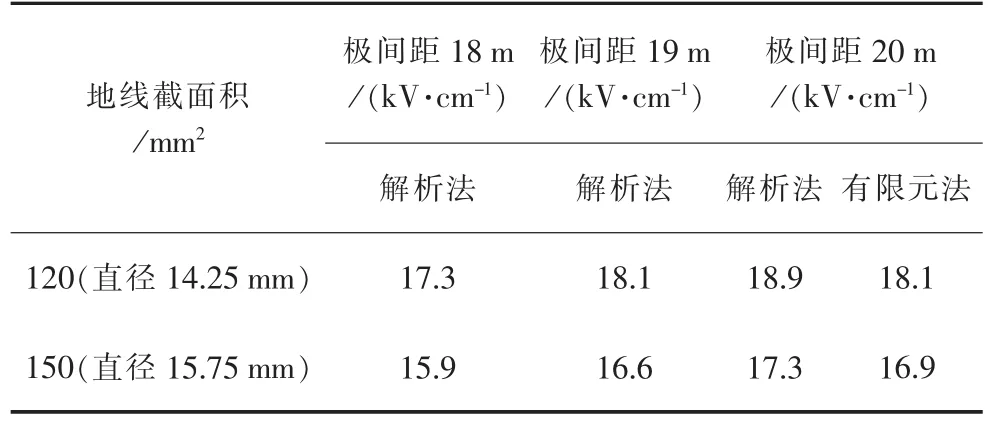
表1 不同极间距地线表面场强

有限元法可形象地表示出计算区域内电场强度的变化（不考虑离子流影响），计算数值较解析法小，在计算中发现，随着划分网格的数量的增大，数值越接近解析法数值，但计算量也随之增大，需合理选择网格数量，满足工程要求即可。

由表1可知，随着极间距的增大，地线表面场强随之增大。

3.3 同保护角时地线表面场强

其他因素不变，计算不同保护角时的地线表面电场强度如表2所示。

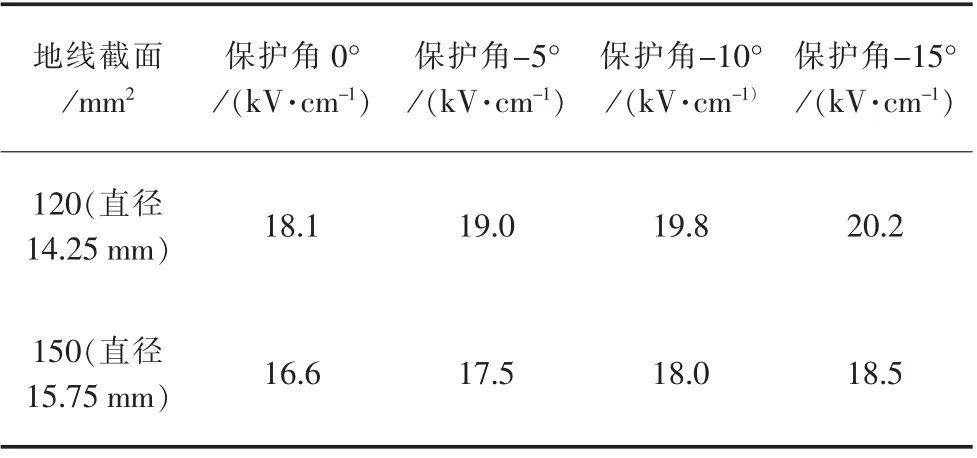
表2 不同保护角地线表面场强

由表2可知，随着地线对导线保护角的增大，地线表面场强随之增大。

3.4 不同对地高度时地线表面场强

其他因素不变，计算不同对地高度时的地线表面电场强度如表3所示。

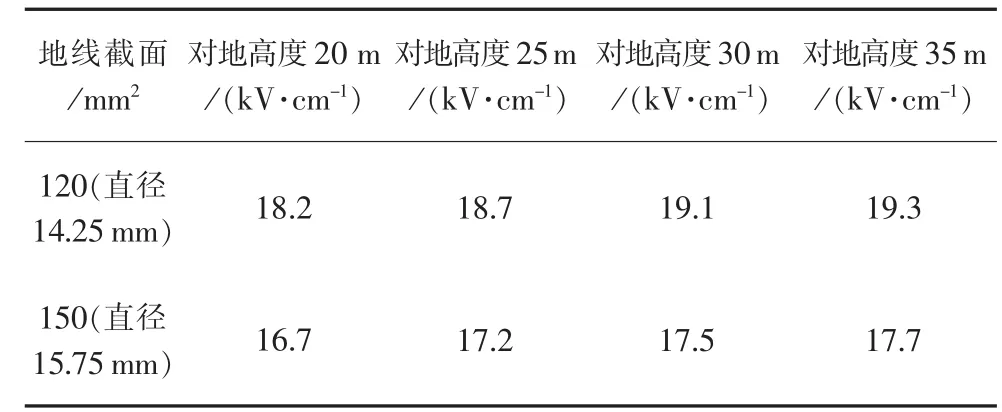
表3 不同对地高度地线表面场强

由表3可知，随着导地线整体对地距离的增大，地线表面场强随之增大，对地超过30m时，增加幅度趋于平缓。

4 结语

解析法只能计算简单形状时的电场强度，而有限元法可以计算形状较为复杂的电场，能形象地表现电场强度的区域分布情况。输电线路与地线之间的距离远远大于地线尺寸，运用有限元法求解时为达到精度需加密网格划分，而网格数量越多计算越慢，因此在计算中应合理进行网格划分。

地线截面的减小、导线极间距的增大、地线保护角的减小、对地距离的增大，均能使地线表面电场强度增大，在选择地线型号时应综合考虑。

从地线表面电场强度角度看，推荐±800 kV山西—江苏特高压直流输电线路工程一般线路采用150mm2地线。