基于SDSM模型的博斯腾湖流域水资源变化模拟

魏光辉

(新疆塔里木河流域管理局，新疆 库尔勒 841000)

0 前 言

内陆干旱区湖泊流域的水资源不仅是当地社会经济发展的重要制约因素，而且是湖泊-流域生态系统赖以存在的基础[1-2]。近几十年来，由于土地资源的大规模开发，人类活动通过修筑大量水利设施拦截入湖地表径流，导致湖泊萎缩、咸化甚至干涸等问题，严重危及湖泊及其相邻区域的生态环境，造成湖泊生物多样性丧失、湖滨地区荒漠化加剧等问题。实施湖泊流域水资源为核心的优化调控战略是改善湖泊生态环境、协调湖泊流域可持续发展和湖泊水资源可持续利用的关键。

鉴于此，本文在前人研究的基础上，以新疆博斯腾湖为例，从气象干旱角度对博斯腾湖近50 a来的变迁进行分析探讨，可为未来气候条件下的湖泊情景提供参照，从而有助于认识中国干旱区湖泊演化趋势，预防或解决目前湖泊流域资源开发利用中出现的问题。

1 数据与方法

标准化降水蒸散指数(Standardized Precipitation Evapotranspiration Index，SPEI)是对月降水量与潜在蒸散的差值进行正态标准化得到的[3]。本次采用国内外较为通用的彭曼(Penman-Monteith)公式计算日潜在蒸散量。计算式如下：

(1)

式中：Rn为地表净辐射；G为土壤热通量；T为平均气温；U2为2 m高度处的风速；es为饱和水气压；ea为实际水气压；Δ为饱和水气压曲线斜率；γ为干湿表常数。

由此可得到逐月的降水量与潜在蒸散量的差值为：

Di=Pi-PETi

(2)

式中：Di为降水与潜在蒸散的差值,mm；Pi为月降水量,mm；PETi为月蒸散量,mm。

对Di数据序列进行正态化处理，并计算对应的SPEI值。由于Log-logistic分布对Di数据序列拟合效果较好，故采用该分布对Di数据序列进行处理。Log-logistic概率分布累积函数为：

(3)

式中：尺度参数α、形状参数β及初始状态参数γ由线性矩法(L-moment)估算：

(4)

(5)

γ=w0-αΓ(1+1/β)Γ(1-1/β)

(6)

式中：Γ(β)为Gamma函数。

原始数据序列Di的概率加权矩w0、w1、w2计算如下：

(7)

(8)

式中：N为参与计算的月份数。

基于式(11)，计算SPEI值，计算式如下：

当P≤0.5时，

P=1-F(x)

(9)

(10)

(11)

式中：c0=2.516，c1=0.803，c2=0.0103，d1=1.433，d2=0.189，d3=0.0013。

当P>0.5时，P由1-P代替，w不变，SPEI变换符号。

SPEI等级划分及相应的累计概率见文献[4]。

2 结果分析

2.1 SPEI趋势分析

首先，从流域角度，对博斯腾湖所在的塔里木河流域1961—2010年SPEI年均值的变化进行分析，结果表明：近50 a来，塔里木河流域SPEI呈显著上升(95%置信水平)趋势并在1986年发生突变(见图1)，显著性检验表明该突变点显著性达到99%置信度水平。

图1 塔里木河流域1961—2010年SPEI均值变化图

2.2 SPEI指数变化对博斯腾湖水位的影响

1955—2010年，博斯腾湖平均水位为1047.03 m，其中最高水位为1 048.90 m，出现在2002年；最低水位为1 044.95 m(出现在1986年)，见图2。由图2可知，博斯腾湖水位与塔里木河流域SPEI指数变化具有一致性，湖水位变化总趋势是：1955—1986年，水位以下降为主；1987—2002年，水位以上升为主，近10 a来水位持续下降。

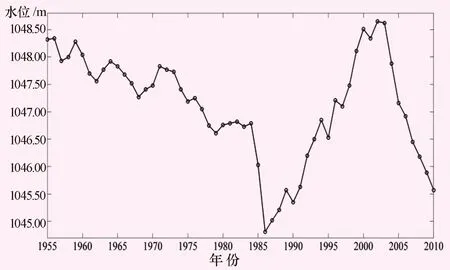
图2 1955～2010年博斯腾湖水位变化图

2.3 博斯腾湖流域径流影响分析

随着全球升温，博斯腾湖流域的水文水资源不可避免地会受到气候变化的影响。博斯腾湖作为实施塔里木河流域生态恢复工程的关键水源地，其源流开都河的出山口径流量的变化不仅对流域经济发展产生影响，同时也将影响到塔里木河下游生态环境恢复，因此在全球大气环流调整过程中，研究未来气候变化情景下博斯腾湖径流量变化具有特殊重要的意义。IPCC列出的SRES(special report on emission scenarios)系列情景[5]中，A2和B2情景分别是高和低排放情景，这2种情景处于合理高和低情况，代表了最常见和合理的情景。因此，本文利用全球气候模式HadCM3在A2和B2情景下的日数据，采用统计降尺度SDSM模型[6-7]，结合HBV水文模型(Hydrologiska Fyrans Vattenbalans model，HBV)对博斯腾湖流域未来径流量进行模拟，并分析其对未来气候变化的响应。

2.3.1 数据来源

博斯腾湖流域地形数据是在SRTM网站(http://srtm.csi.cgiar.org)下载的90 m×90 m的DEM数据。土地利用数据选取中国科学院资源环境科学数据中心提供的1986年和2000年2期研究区1∶100 000土地利用类型数据。开都河流域气象观测数据为中国气象局国家气候中心提供的开都河流域内和附近的6个气象测站(巴音布鲁克、巴仑台、轮台、焉耆、和静、和硕)逐日最高、最低及平均气温、日降水数据。覆盖塔里木河流域的NCEP数据(1961—2001年)和英国Hadley气候预测与研究中心的全球气候模式HadCM3在A2和B2情景下的气候要素日数据，其中A2反映区域性合作，对新技术的适应较慢，人口继续增长；B2假定生态环境的改善具有区域性。NCEP数据经过网格再划分与HadCM3的网格尺度一致(见图3)，它包含了500 hPa和850 hPa高度场、比湿、经向风速、纬向风速、涡度以及海平面气压等环流因子。

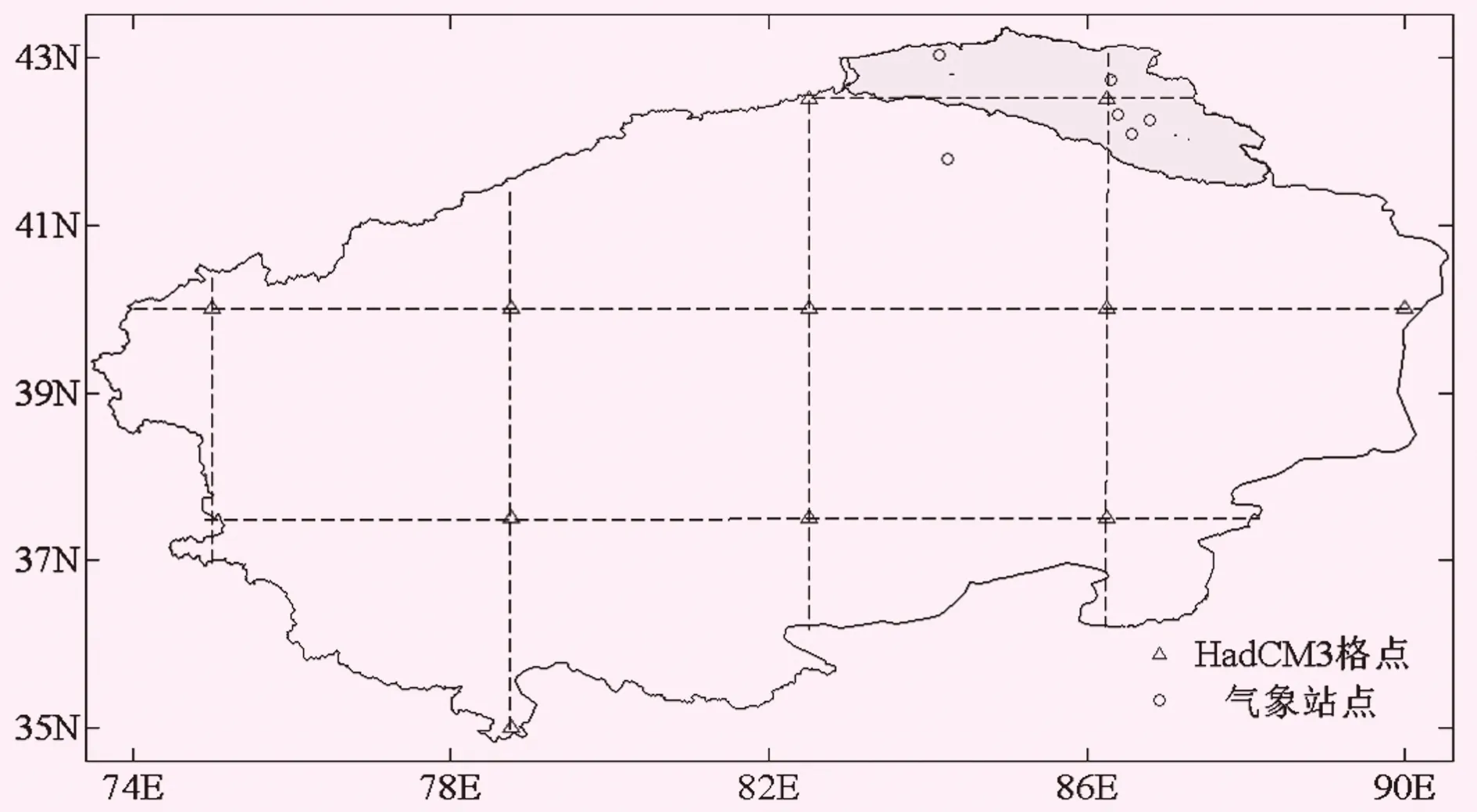
图3 HadCM3在塔里木河流域和开都河流域格点分布图

2.3.2 HBV-D建模

(1) HBV-D模型参数率定

模型性能使用Nash效率系数R2值来判断，当数据拟合完美时R2=1，其计算式如下[8]：

(12)

使用相对误差r来评价模型模拟精度，相对误差r值越小表示模拟精度越高，反之则表示误差较大。

(13)

利用HBV模型对开都河流域出山口(大山口水文站)径流量进行模拟，选取该水文站1967—1987年日降水量、日最高气温、日最低气温、日蒸发皿蒸散发和日径流量数据以及研究区1980年的土地利用类型数据进行参数率定。其中，日蒸发皿蒸发量数据也可使用月均值。参数率定结果表明，径流模拟对气温、降水随海拔递减率、BETA值、上层土壤的快速和慢速消退系数(KUZ2、KUZ1)、下层土壤的消退系数(KLZ1)、直接径流阈值(UZ1)、下层土壤下渗能力(PERC)等参数响应敏感。对月尺度的模拟结果分析得出，R2=0.64，r=2.79%。从率定结果来看，率定期(1967—1987年)日径流量模拟最大相对误差为18.78%，最小相对误差为0.22%，平均相对误差为4.67%，Nash效率系数为0.63，模型总体模拟效果较好，率定后的模型可以用于开都河流域径流预测。

(2) HBV-D模型验证

选取2000—2007年为模型验证期，由于研究区海拔较高，受人类活动影响相对较小，因此验证期土地利用类型数据采用2000年数据。对验证期的月尺度模拟结果分析得出：R2=0.60，r=5.32%。从验证结果来看，验证期(2000—2007年)日径流量模拟最大相对误差为55.46%，最小相对误差为1.39%，平均相对误差为7.82%，Nash效率系数为0.57，部分时段的模型模拟效果并不好，特别是验证期的开始年份，其原因主要包括：模型模拟预热、气象站点的空间分布密度、DEM和土地利用类型数据等空间分辨率以及模型参数率定过程中存在的不确定性等因素。总体来说，模型经参数率定后，验证结果有着较好的精度。

2.3.3 径流对未来气候变化的响应

(1) 未来气候情景生成

首先是预报因子的选择。根据筛选的结果可以发现，无论是日最低、最高气温，还是日均气温，筛选出的偏相关系数绝对值较高(0.6～0.9之间)的前3个预报因子均是mslp(平均海平面气压)、p500(500 hPa位势高度)和temp(平均气温)；而相对于气温，降水量筛选的预报因子较多，包括p5_vas(500 hPa经向风速)、zas(涡度)、shum(地表比湿)、r500(500 hPa的相对湿度)等，但与预报因子之间的偏相关系数绝对值比较低(0.1～0.2之间)。其次是对SDSM模型的率定和验证，SDSM模型采用解释方差和标准误差来反映预报量与环流因子之间的关系[9]。模型的解释方差表示预报量与预报因子之间的相关性大小，而标准误差则反映预报量对预报因子的敏感性。

综合不同类型的步进式直线压电驱动器来看，从性能上，行走式压电驱动器与推动式压电驱动器输出驱动力较大，速度较慢，驱动频率较低，步距可在大范围内调整，而摩擦惯性式压电驱动器输出驱动力较小，但速度快，频率高。

表1列出了模型率定期(1961—1990年)流域各站点日最高气温、最低气温和日平均气温的解释方差(r2)和标准误差(SE)。由表1可知，筛选的环流因子对日最高气温和日平均气温的方差解释较好，所有站点的解释方差都在40%以上。但对降水的方差解释略差，模型解释方差在0.1～0.25之间。

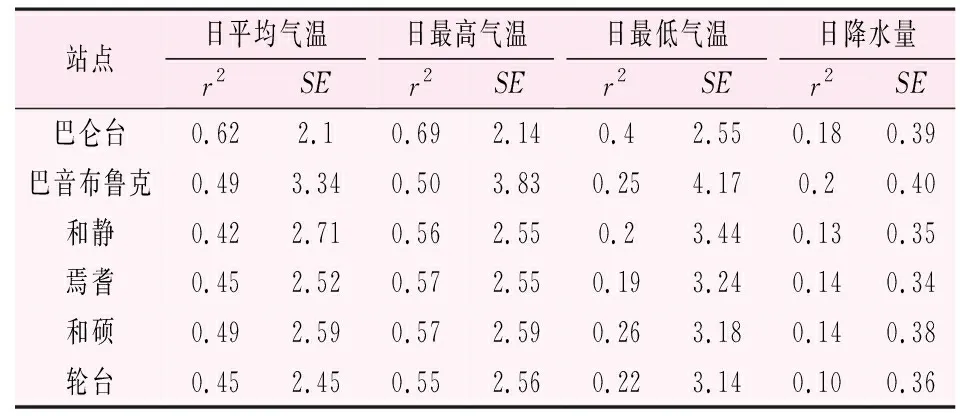
表1 SDSM 模型率定的各站解释方差(r2)和标准误差(SE)表

验证期采用1991—2000年各站点数据和NECP数据进行分析。采用相关系数(r1)和效率系数(Ce)来检验模型精度，检验结果见表2和图4。

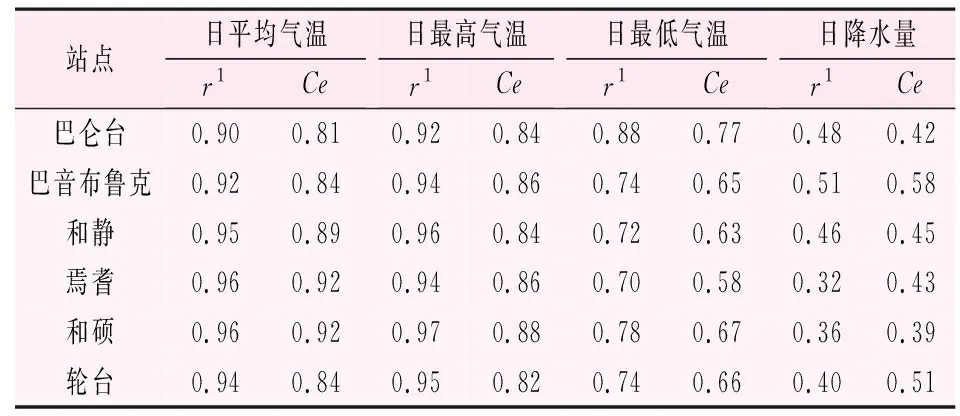
表2 SDSM模型验证的各站相关系数(r1)和效率系数(Ce)表

由表2与图4可知，SDSM模型的气温模拟能力较好，对日降水的模拟量值偏小，这可能是在一定程度上受验证时段(1991—2000)流域降水相对于率定时段(1961—1990)显著增加有关。

最后生成未来气候情景：A2、B2情景下气温、降水数据相对于基准期的变化，见表3。

表3 不同情景下6站平均日最高、最低、平均气温及年降水量相对于基准期变化表

从表3可以看出，未来日平均、日最高气温在2种情景下均呈上升趋势，日最低气温在B2情景下呈下降趋势，2种情景下的年降水量在2020年、2030年均呈下降趋势，在2010年几乎无变化。

(2) 未来径流量模拟

利用上述经SDSM模型模拟的未来气候情景数据，结合HBV-D模型对未来径流量进行模拟(见图5)。可知，在A2情景下，开都河流域出山口日径流量呈下降趋势；在B2情景下，日径流量在2010年时段呈现增加趋势，在2020年和2030年呈持续下降。将日径流量合成年径流量进一步分析其在2012—2038年的变化：在A2、B2情景下，该时段年径流量均呈现显著下降趋势；在B2情景下，在2010年径流量呈现增加趋势。

结合未来径流量预测结果可以看出，2种情景下模拟出的年径流平均值在2010年更接近基准期实测数据计算值。由于SDSM模型在博斯腾湖流域降水方面的模拟效果不是太好，因此在未来径流量变化趋势上仅能简单评论，对于未来径流量模拟精度的提高，还需采用更高精度的日降水量预测数据。

3 结 语

(1) 近50年来，塔里木河流域SPEI指数呈显著上升趋势并在1986年发生突变。

图4 巴仑台站日均气温及降水量验证结果与实测数据比较图

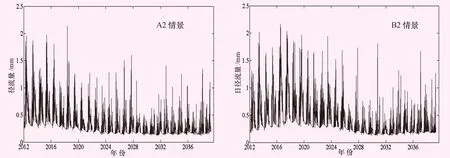
图5 未来日径流量的变化图

(2) 博斯腾湖水位与塔里木河流域SPEI指数变化具有一致性，湖水位在1955—1986年间以下降为主，1987—2002年间以上升为主，近10年来水位持续下降。

(3) SDSM模型气温模拟能力较好，对日降水的模拟量值偏小，未来日均、日最高气温在A2、B2两种情景下均呈上升趋势，日最低气温在B2情景呈下降趋势；2种情景下的年降水量在2020年和2030年均呈下降趋势，在2010年几乎无变化；在A2情景下，开都河流域出山口日径流量呈下降趋势，在B2情景下，日径流量在2010年时段呈现增加趋势，在2020年和2030年呈持续下降趋势。