橡胶材料超弹性本构模型选取及参数确定概述
钱 胜,陆益民,杨咸启,吴承伟
(1.黄山学院 机电工程学院,安徽 黄山 245041;2.合肥工业大学 机械工程学院,安徽 合肥 230009)
橡胶材料具有弹性好和阻尼高等特点,是高性能的阻尼材料,广泛应用于工业、建筑和国防等领域。
在对橡胶材料的深入研究中,一直尝试对其力学行为进行真实描述,但是由于橡胶分子结构和橡胶材料组成比较复杂,橡胶材料及其几何和边界的非线性,而且橡胶材料对于温度、介质、时间、载荷率和应变等因素影响的敏感性,使得建立精确计算橡胶材料力学行为的数学模型十分困难[1]。目前橡胶材料力学行为计算采用比较复杂的数值技术,其计算精度与所使用本构模型正相关。随着计算力学的快速发展和橡胶材料应用的需求增大,将研究出更为精确、实用且能与有限元分析理论融合的本构模型[2]。
橡胶材料一般添加补强体系、防护体系和硫化体系等,硫化后形成三维交联网络结构。在外加载荷作用下,橡胶材料表现出非线性、大变形、超弹性、粘弹性、Payne效应和 Mullins效应等特性,其力学行为异常复杂[3]。研究橡胶材料真实力学行为对于橡胶制品的研制十分重要。如果能根据橡胶材料组分、橡胶制品工作状态和环境,选取合适的橡胶材料超弹性本构模型和获取较为精确的模型参数对橡胶减振制品的减振性能、力学性能以及疲劳寿命研究意义重大。
1 橡胶材料超弹性本构模型分析
橡胶材料具有体积近似不可压缩性,在外界载荷作用下表现出弹性变形,卸载后可恢复原形,这种行为称为超弹性。超弹性本构模型分为两大类:基于连续介质唯象理论模型和基于热力学统计方法模型。
1.1 基于连续介质唯象理论模型
连续介质力学描述所观察到的橡胶材料性质是采用橡胶材料内部应变能来描述的,而不是在聚合物分子结构基础上表征的,其核心是建立体系内贮存弹性能表达式[4]。基于连续介质唯象理论模型有两种形式,一种是采用应变不变量I1,I2,I3表征应变能(E)函数形式:
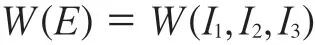
这种形式超弹性本构模型有Mooney-Rivlin模型、Neo-Hooke模型、Yeoh模型、Gent模型、高玉臣应变能函数模型、Isihara模型、Gent-Thomas模型、Swanson模型、Arruda-Boyce模型、Yeoh-Fleming模型、Carroll模型、Hart-Smith模型、Alexander模型、van der Waals模型、Pucci-Saccomandi模型和Lopez-Pamies模型[5-8]。
另一种基于连续介质唯象理论模型是基于伸长率的连续介质模型,其应变能函数可用主伸长率来表征,该形式模型有Ogden模型、Shariff模型和Attard模型[9]。
在这些超弹性本构模型中,适用于有限元分析的模型有Mooney-Rivlin模型、Neo-Hooke模型、Yeoh模型、Arruda-Boyce模型和van der Waals模型。
1.2 基于热力学统计方法模型
分子统计学理论认为橡胶材料的应力-应变行为主要由构象熵决定,该理论假设橡胶大分子是随机取向的长链分子,并通过分子链节点处的化学交联而形成交联网络结构[1-4,10]。基于热力学统计方法超弹性本构模型有高斯统计模型和非高斯统计模型。
1.3 本构模型改进和创新
好的超弹性本构模型是易于通过材料试验数据获得少量模型参数的本构模型,而且能够较准确描述材料的所有力学行为[11]。但是原有的超弹性本构模型都存在一定局限性[1-2]。为此,国内外学者结合具体橡胶制品设计及工程应用经验,对一些原有超弹性本构模型进行改进或者提出新本构关系。刘峰等[12]研究橡胶材料在大应变时表现出应力-应变增强或软化效应,提出用一种新的应变能函数来描述橡胶材料大变形硬化本构关系,并确定了橡胶材料硬化时的本构模型参数。李雪冰等[13]针对Yeoh模型拟合橡胶材料大变形条件下力学行为不理想,尤其在预测等双轴拉伸试验曲线时出现“偏软”现象,提出一种改进Yeoh模型,改进本构模型保持了Yeoh模型的特性,在反S形应力-应变关系的条件下,有效克服了预测等双轴拉伸曲线的“偏软”问题。
文献[14]提出在试验的整个变形区域内精确预测3种变形模式的应力-应变关系的新超弹性本构模型:

式中,λi(i=1,2,3)为主伸长率,C-1,C1和Cn为模型参数。
该模型参数通过橡胶材料均匀试样的等双轴拉伸试验获取,该模型适应于有限元分析。
罗文波等[16]引入权重函数,用高斯链网络模型描述小变形的同时,用八链网络模型描述大变形,提出了基于高斯网络模型与八链网络模型的混合本构模型。
2 橡胶材料超弹性本构模型选用
超弹性本构模型在理论、特点和适用范围上都已有较深入的研究[1-2,17-18]。橡胶材料超弹性本构模型选取的出发点有材料试验、有限元分析适应性、橡胶制品力学计算精度等。
从材料试验角度选取超弹性本构模型,一般要完成橡胶材料3项基础试验(单轴拉伸试验、等双轴拉伸试验和平面拉伸试验)。K. Beomkeun等[19]采用Neo-Hookean模型、Mooney-Rivlin模型和Ogden模型反映氯丁橡胶力学行为,通过拟合3项基础试验以及4组组合试验数据,优选出拟合精度高的模型。H.Mokarram等[20]对当时所有现象学和热力学统计学超弹性本构模型进行了分析和比较,采用一致切线化处理,得出所有超弹性本构模型的切线算子作为有限元分析本构模型的选择依据。龚科家等[21]开发出一种基于图像分析的完整橡胶材料参数试验系统,并以载重轮胎的橡胶材料为对象进行3项基础试验和多种模型拟合,验证了该系统的可靠性、稳定性和计算精度都较高。胡小玲等[22-23]研究炭黑填充橡胶材料在3项基础试验齐全和不齐全条件下超弹性本构模型选取策略和拟合精度。结果表明:在3项基础试验齐全的情况下,依次优选Ogden模型[阶数(N)=3]、Yeoh模型和Arruda-Boyce模型;只有两项基础试验(含等双轴拉伸试验)得出的Ogden模型(N=3)拟合精度高;仅有单轴拉伸试验时,Arruda-Boyce模型拟合精度高;等双轴拉伸试验和平面拉伸试验是确定较为精确的本构模型参数的必备试验。上官文斌等[24]研究汽车动力总成橡胶隔振器弹性特性,建立橡胶主簧超弹性本构关系,得出材料试验曲线拟合基本原则:材料试验的应变类型和范围应尽可能反映橡胶制品实际使用应变情况;尽可能选用低阶的应变能函数拟合;检查本构模型拟合曲线与试验曲线的一致性。陈志勇等[25]以汽车橡胶悬置为对象,在处理材料试验数据时采用Savitzky-Golay方法处理,有效避免了试验条件限制和错误数据对拟合结果影响,得出材料的Drucker稳定性条件。材料稳定性是评价由试验数据建立的橡胶材料超弹性本构模型优劣的重要依据,也是选择本构模型的基点。
以有限元分析计算精度为依据选取橡胶材料超弹性本构模型。王文涛等[26]通过研究不同应变下橡胶材料超弹性本构模型拟合精度,发现Mooney-Rivlin模型比其他模型具有更稳定的计算能力;通过采用超弹性本构模型对汽车橡胶隔振器静态特性预测发现,Mooney-Rivlin模型在较小应变下具有较高的计算精度和迭代收敛性,van der Waals模型和3阶Ogden模型在处理较大应变数据时计算精度较高。文献[27]研究在多载荷条件下橡胶隔振器的模型建立,采用Mooney-Rivlin模型、van der Waals模型和Marlow模型计算承受单载荷和多载荷下两种橡胶隔振器的静刚度。
为减少有限元分析中超弹性本构模型选取的盲目性,提高橡胶制品性能预测可靠性,王国权等[28]研究橡胶工程中常用的3种超弹性本构模型有限元分析的适应性,即由标准试样单轴拉伸试验数据拟合Mooney-Rivlin模型、Ogden模型及Yeoh模型参数,得出在小应变(≤100%)下3种超弹性本构模型适应性:Mooney-Rivlin模型较好,Yeoh模型次之,Ogden模型较差;在较大应变(大于100%)下Ogden模型和Yeoh模型适应性较好,而Mooney-Rivlin模型较差。李炼等[29]探讨土木减振结构使用的3种橡胶材料超弹性本构模型与有限元分析的匹配度,通过橡胶圆柱试样单轴压缩试验,经模型参数的有限元计算得出:在橡胶试样压缩时,Neo-Hooke模型适用于0~45%的压缩应变,Mooney-Rivlin模型和Yeoh模型适用于不小于60%的压缩应变。
李凡珠等[30]分析循环加载/卸载条件下填充炭黑橡胶材料的力学行为发现:在加载条件下Marlow模型拟合精度高;在卸载条件下Mullins模型拟合精度高,用反推法可较好拟合卸载条件下试验曲线,然而Mullins模型不能反映橡胶材料永久变形行为;在卸载条件下采用体现塑性变形的模型与Mullins模型叠加拟合的曲线与试验曲线拟合精度较高。
3 橡胶材料超弹性本构模型参数的确定
橡胶材料超弹性本构模型参数确定方法主要有:①基于简单材料试验的本构理论计算法;②基于完整材料试验的数值拟合法;③根据已有橡胶材料特性的识别法,如反推法;④先进材料参数试验法。
国内早期没有完善材料试验设备,确定超弹性本构模型参数主要是通过简单材料试验和本构理论计算法获取。何春明等[31]对坦克负重橡胶材料进行有限元分析,提出一种测定橡胶材料Mooney-Rivlin模型参数的方法。
郑明军等[32]探讨橡胶材料硬度与力学常数的关系,得出Mooney-Rivlin模型参数计算方法。左亮等[33]依据橡胶材料的硬度与力学参数经验公式,通过材料理论确定Mooney-Rivlin模型参数。黄建龙等[34]选取两参数Mooney-Rivlin模型和Yeoh模型,利用线性回归拟合单轴拉伸试验曲线,确定橡胶材料应力-应变参数,并通过有限元分析验证。王利荣等[35]进行橡胶隔振器静态特性及有限元建模研究,建立橡胶材料的Mooney-Rivlin模型,即依据橡胶材料试验国家标准,在通用材料试验机上进行橡胶材料的单轴拉伸试验和压缩试验,确定模型参数。
随科学技术水平提高,国内可以完成一定的材料基本试验,并制定了系统的橡胶材料试验国家标准。橡胶材料本构模型参数可以利用数值分析技术中最小二乘法拟合已有橡胶材料试验数据来确定。伍开松等[36]研究丁腈橡胶胶筒在大变形下的力学性能,通过选择本构模型,利用最小二乘法拟合模型参数,得出评价本构模型优劣公式。张平等[37]测试不同受力状态下橡胶材力学性能,获得橡胶材料在不同受力状态下的应力-应变曲线,采用最小二乘法拟合不同本构模型参数。上官文斌等[38]计算橡胶扭转减振器的滑移转矩,根据扭转减振器在实际工况下承受的压缩和剪切变形,选择单轴拉试验和平面拉伸试验,用最小二乘法拟合本构模型参数。徐中明等[39]采用超静定方程方法确定橡胶材料超弹性本构模型参数,该方法拟合精度比最小二乘法高。
从国外引进的隔振器无法通过国内传统方法制备标准橡胶试样以获取橡胶材料模型参数,因此国内研究人员利用反推法确定橡胶材料超弹性本构模型参数。楼京俊等[40]研究进口橡胶隔振器时,采用反推法确定橡胶材料参数,选择两参数Mooney-Rivlin模型,基于Matlab和ANSYS软件联合仿真技术,根据硬度与力学参数的经验关系式确定本构模型参数。刘文武等[41]在无法获取标准橡胶材料试样条件下研究橡胶隔振器有限元计算,提出一种根据橡胶隔振器总成试验数据,利用多目标优化软件iSIGHT确定橡胶材料应变能密度函数的方法。
朱艳峰等[42]利用粒子群优化算法确定橡胶材料大应变时硬化现象的本构模型参数,用改进型粒子群算法拟合单轴拉伸试验数据,与传统最小二乘法拟合相比,改进型粒子群算法拟合速度快,精度高,能够解决试验数据曲线不光滑或有拐点而导致不收敛的问题。张军等[43]研究汽车减震系统中缓冲橡胶块的刚度、强度和疲劳特性,由于很难通过橡胶材料试验准确获取材料参数,提出了基于最小二乘法响应面法,结合有限元仿真技术,反求出Mooney-Rivlin模型参数。陈宝等[44]研究轿车橡胶衬套力学行为,由于缺少基础试验数据,无法建立本构模型,因此根据结构试验获取橡胶衬套3个方向位移-力曲线的非完全试验信息,利用HyperStudy和Abaqus软件技术分析试验与仿真曲线的一致性;选择Yeoh 多项式模型,采用自适应响应面法,经过多次迭代识别出一组能较准确模拟橡胶衬套力学行为的材料参数。
国外学者对橡胶材料超弹性本构模型参数确定进行了深入研究。S.Hartmann等[45]研究一种获取橡胶材料超弹性本构模型参数的光学测量法,并验证光学测量法获取的参数准确性。M. Rachik等[46]为了克服橡胶材料与橡胶制品具有相同边界条件以及橡胶材料均匀变形的缺点,采用反推法确定橡胶材料参数。E. H. Twizell等[47-48]发现对六参数或八参数Odgen模型采用非线性最小二乘优化法很难实现收敛,主要是很难确定优化初始值。Y.Kamel等[15]提出一种四参数超弹性本构模型,该模型参数的确定可以转化为线性优化问题,初始值设定任意正值,使得优化结果收敛。B.Tibi[49]提出采用分阶段模型与最小二乘法联合方法拟合橡胶材料超弹性本构模型,该方法可以应用于有约束条件的求解过程,同时将非线性问题转化为线性问题求解。
随着科技进步,橡胶材料超弹性本构模参数确定方法不断更新,从早期基于简单材料试验的理论计算法,发展到基于完整材料试验的数值拟合法和先进材料参数试验法,模型参数精度有较大提高,必将促进减振橡胶制品的设计与力学性能计算精度有较大提升。
4 结语
本文以橡胶材料超弹性本构模型为对象,从本构模型选用和本构模型参数确定方法两个方面分析和总结国内外学者研究成果。橡胶材料超弹性本构模型发展目前主要存在以下问题:①本构模型类型较多,没有较为统一的形式,且各本构模型有一定使用条件,模型选取需要进行繁琐材料试验,工作量大;②本构模型建立较多涉及材料变形、硬化、粘弹性和试验数据拟合精度等,而很少涉及Payne效应、Mullins效应以及裂纹扩展和断裂、磨耗、老化等因素;③基于橡胶材料试验所建立的本构模型计算结果与橡胶件总成试验结果有一定偏差。解决这些问题对橡胶制品设计及力学性能计算具有非常重要意义。

