压缩感知中基于FADMM的l1-l1范数信号重构
高雷阜 徐 部
(辽宁工程技术大学理学院 辽宁 阜新 123000)
0 引 言
压缩感知[1-3]CS(Compressed Sensing)是E.Candès、T.Tao等提出的一种寻找欠定线性系统稀疏解的技术。其核心思想是:若原始信号经某些正交变换(如小波变换,傅里叶变换)后满足稀疏或近似稀疏性,则可以将信号投影到低维空间,再通过最优化方法较为精确地实现信号重构。CS理论为降低信号采样成本、减少数据存储传输代价带来了新契机,已广泛应用于遥感图像[4]、医学成像[5]和无线传感器网络[6]等众多领域。
在CS理论中,信号重建的作用至关重要,其目标是寻求计算复杂度低且能够实现信号精确复原的算法。一种直观的重构方法是求解l0-正则化问题,即利用信号满足稀疏性的先验信息,在欠定线性系统中寻求具有最稀疏性的信号,但该求解方式难以计算。因此,当信号足够稀疏且不含噪声时,常采用与之等价的基追踪BP[7]方法重建信号。然而,在许多实际问题中,信号会受到噪声干扰。对于含高斯噪声的信号,CS理论将BP算法转化为极小化l1-l2范数BPDN(Basis Pursuit Denoising)问题求解。但是当噪声具备稀疏结构(如脉冲噪声)时,该类方法很难实现信号的精确重建[8]。
为此,文献[9]用l1-范数拟合项取代BPDN中的l2-范数拟合项,提出一种l1-l1模型,将其应用于人脸识别问题并取得较好效果,但该文献通过线性规划方法求解l1-l1模型,因而求解速度较慢;文献[10]提出DADM(Dual-based Alternating Direction Method),该方法将l1-l1模型转化为等价的BP问题,并采用交替方向乘子法ADMM(Alternating Direction Method of Multipliers)[11-12]求解,结果表明若信号中含有大量脉冲噪声,相比于BPDN方法,DADM能够更好地实现信号重建。但该算法要求感知矩阵行正交以使其收敛。然而,对于l1-l1范数极小化问题,感知矩阵通常为随机阵,很难满足这一条件[13]。因此,本文提出采用一种带有“重启动”策略的快速交替方向乘子法FADMM[14]求解l1-l1问题以实现信号重构。该算法在求解过程中无需将l1-l1模型转化为BP问题且不要求感知矩阵满足行正交性,同样适用于受到大量脉冲噪声及少量高斯白噪声干扰的信号重构问题。
1 压缩感知基本理论
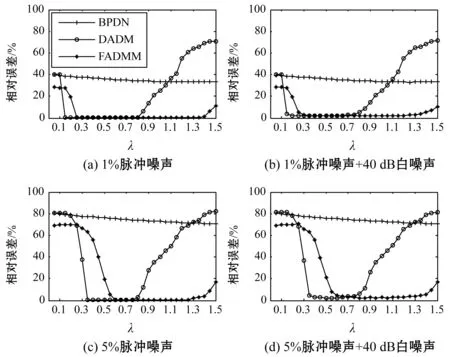
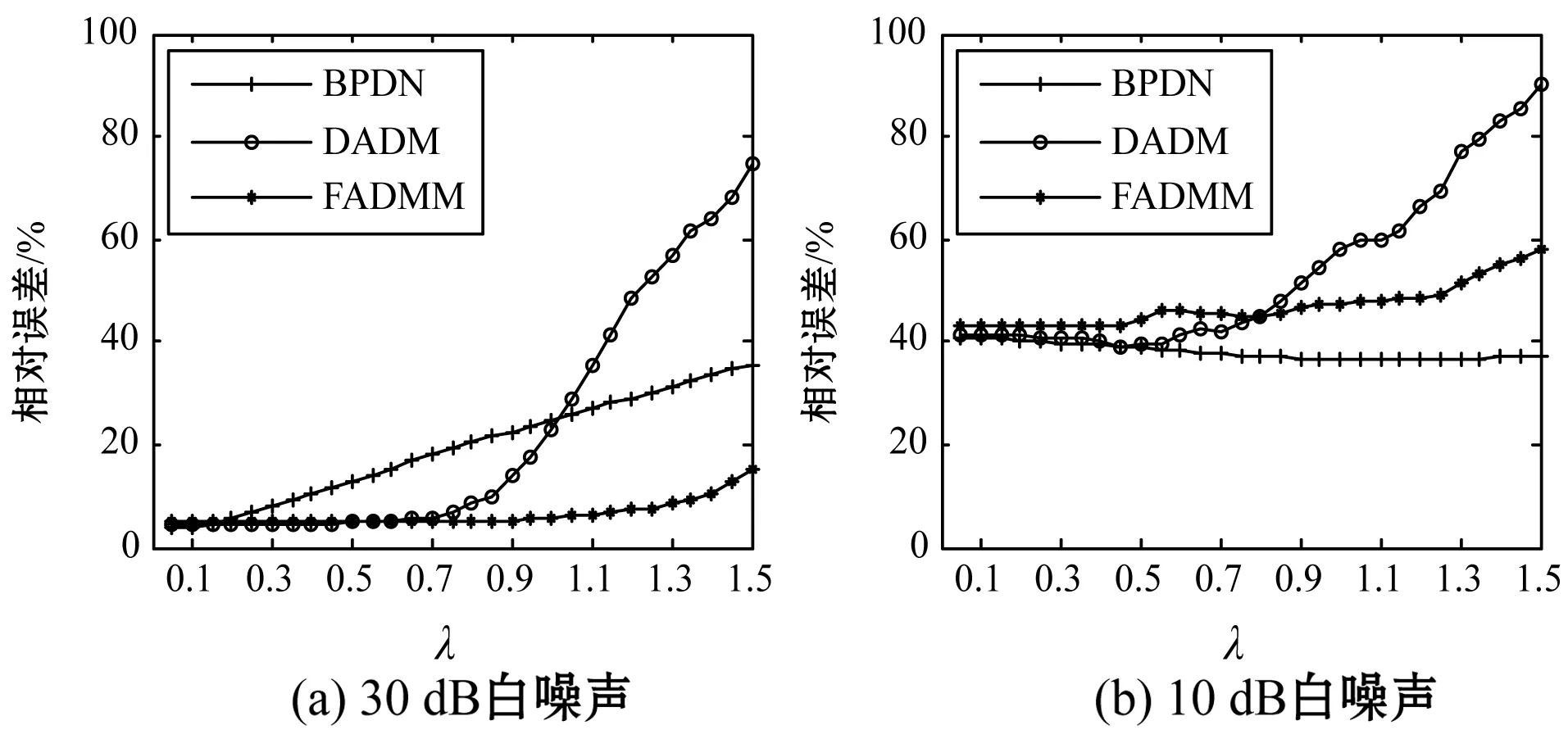
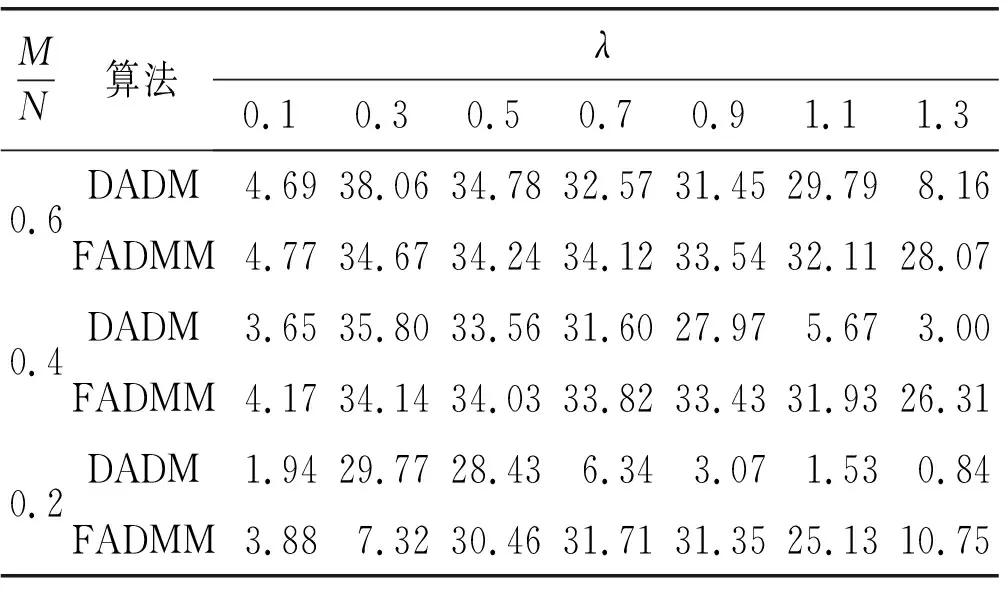
任给信号f∈RN×1,若其在一组标准正交基底Ψ={ψ1,ψ2,…,ψN}下能够稀疏表示为f=Ψx,其中x∈RN×1为Ψ域的稀疏系数,则可通过与Ψ非相干的测量矩阵ΦM×N(M< b=ΦΨx=Ax (1) 称A=ΦΨ为感知矩阵。对于无噪信号,Chen等[7]提出可采用BP算法求解式: min{‖x‖1:Ax=b} (2) 若b受到噪声干扰,则很难由上式较为精确地实现信号重建。因此,将式(2)中的约束条件进行松弛处理,转化为有约束形式的BPDN问题: min{‖x‖1:‖Ax-b‖≤δ} (3) 式中:δ>0是噪声水平的上界。由于可将无约束的式(3)作为二次规划问题求解[15],所以通常采用其无约束形式重建信号: μ的作用为平衡正则与拟合项。文献[10]提出,若信号中含有脉冲噪声,求解极小化l1-l1范数问题: min‖Ax-b‖1+λ‖x‖1 (4) 能够取得更好的重构效果,其中λ>0为正则参数。该类问题也被应用于图像修复[16]、人脸识别[17]等领域。 ADMM融合了对偶上升法与乘子法的优点,适用于求解大规模凸优化问题[11]。该算法所求问题的形式如下: minf(x)+g(z) s.t.Ax+Bz=b (5) 式中:A∈RM×N,B∈RM×P,b∈RM×1,f和g为凸函数。式(5)的增广Lagrangian函数可表示为: Lρ(x,z,y)=f(x)+g(z)+yT(Ax+Bz-b)+ (ρ/2)‖Ax+Bz-b‖2 式中:y∈RM×1是对偶变量,ρ>0为罚参。与乘子法通过最小化Lρ(x,z,y)来同时求解两个原始变量的方式不同,ADMM引入单步高斯-赛德尔策略,固定其余变量,交替更新x和z: (6) 直至满足迭代终止要求,得式(5)所求解。 在实际环境下,信号中通常含有噪声。当信号及干扰噪声同时满足稀疏性时,通过求解l1-l1模型能够更好地实现信号重建。虽然该模型是一个凸问题,但由于l1范数仅满足弱凸性且不可导,因而很难对l1-l1范数极小化问题进行求解。本文提出采用一种带有“重启动”规则的FADMM算法来解决l1-l1范数极小化难以求解的问题。 具体的求解过程为:采用变量分裂方法,将式(4)转变为约束优化问题: minλ‖x‖1+‖z‖1s.t.Ax+z=b 令f=λ‖x‖1,g=‖z‖1,B=I,并用式(6)对其求解。固定z、y,更新x: (7) 由于感知矩阵A的存在,使式(7)不存在解析解,因而在xk-1点处线性化二次项并加入迫近项可得: xk= arg minxλ‖x‖1+ Τλtk/ρ(xk-1-tkgk) 更新对偶变量: yk=yk-1+ρ(Axk+zk-b) 与ADMM算法不同,FADMM沿用Nesterov梯度下降法[18]中的加速思想,对zk和yk进行二次更新: 若迭代过程中满足ck<ηck-1(η为递减因子),则执行zk和yk的二次更新;否则,抛弃当前代,将k-1代信息作为新的起始点,重新开始算法,以使其联合误差不增加,因而保证了FADMM的全局收敛性。但由于式(7)在求解过程中采用了线性逼近方法,由文献[12],本文中联合误差定义为: 本数据采集系统中设计的总线长32 m,每隔1 m接入一个从站单元,测试时在A1从站的第3通道接入3 V的电压,其余通道和从站悬空,发送查询指令后上位机收到的数据如图9所示。 算法的流程如下所示。 算法1FADMM求解l1-l1模型步骤 1:xk=arg minxLρ(Xk-1,zk,yk) 2:zk=arg minzLρ(Xk,z,yk) 5: ifck<ηck-1then 9: else 11:ck←η-1ck-1 12: end if 13: 判断是否满足终止条件 ,若满足则停止;否则,令k=k+1,转步骤1. 式中:x是原始信号,x*为重建信号。 当信号中含有脉冲噪声时,随着正则参数的变化,三种算法计算所得相对误差如图1所示。 图1 脉冲噪声下信号重建误差 由图1可见,当信号中含有少量脉冲噪声时,由于FADMM和DADM都是对l1-l1模型进行求解,所以两种方法的信号重构结果在整体上好于BPDN算法。但随着正则参数λ值的增大,DADM所得相对误差出现了明显的增加,当λ>1.1时BPDN算法重构结果比DADM更好一些,而FADMM受正则参数变化的影响较小,当λ>1.3时相对误差才略有增加。随着脉冲噪声的增大,BPDN所得相对误差在正则参数的变化过程中相对较大,而FADMM在正则参数较大时能够得到更好的重构结果。 为更好地验证FADMM的重构效果,取λ=0.7,采用该算法对含有5%脉冲噪声的信号进行重构,重构效果见图2。 由图2可见,当信号中含有大量脉冲噪声时,FADMM获得了较好的重构效果,即能够实现原始信号与重构信号间的高度重合。由图3(a)可见,对于白噪声为30 dB的信号,BPDN所得相对误差呈线性递增趋势;当λ>0.7时DADM已出现相对误差增加,而当λ>1.1时FADMM开始出现相对误差增加。随着白噪声的增大,BPDN逐渐显露其优势。 图3 白噪声下信号重建误差 表1 R对比结果 由表1可见,随着正则参数增加,两种算法计算所得R均呈现先增后减的变化趋势。由于DADM将l1-l1模型转化为BP问题,其在具体求解过程中正则参数会直接影响原始及对偶变量的结果,因而该算法所得R更易因正则参数的变化而改变。在λ=0.5处DADM开始出现重构信噪比减少,且递减幅度较大,而FADMM在正则参数从0.3增加至1.1的过程中R变化幅度较小,因而整体上FADMM的重构结果好于DADM算法。随着采样率的减小,DADM更易得到低R。相比于DADM算法,FADMM能够适应不同λ下的信号重构。 针对极小化l1-l1范数难以求解的问题,本文采用FADMM对该模型求解。利用变量分裂技术,将l1-l1模型转变为约束优化问题,采用单步高斯-赛德尔思想,交替更新原始及对偶变量,并对变量执行二次更新,引入重启动规则以保证FADMM全局收敛,直至满足终止要求,所得结果即为重构的最优解。实验结果表明,对于含大量脉冲噪声及少量白噪声的信号,本文方法均能较好地实现重构。下一步的计划是将极小化l1-l1模型应用于含噪图像重建等问题。2 快速交替方向乘子法(FADMM)
2.1 交替方向乘子法(ADMM)
2.2 带有“重启动”规则的FADMM
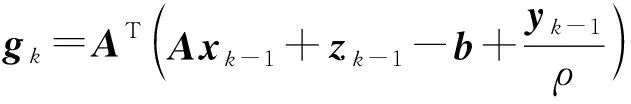
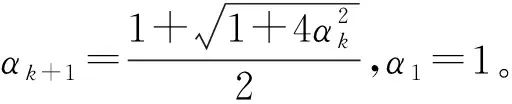
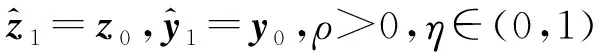

3 实验结果及分析
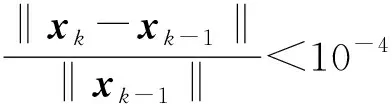

4 结 语

