ES_SSE: 一种文本重复检测方法

杨 荣 李 兵 王电化 吴 谋 邓树文

1(湖北科技学院计算机科学与技术学院 湖北 咸宁 437100) 2(武汉大学国际软件学院 湖北 武汉 430079)

0 引 言

如今，随着智能时代的到来，软件服务生态发生了很大的变化，Web信息呈爆炸式增长，同时也造成网络中存在海量的相似页面。这些海量的相似性内容，不仅浪费检索资源，而且也不便于人们的使用。因此，以此为背景，本文研究一种高效的网页重复检测方法。

对于两个页面，通过shingling每一个文档，能够得到相关词汇大小构成的集合，即w-shingling集合(w为给定的词汇组合个数)，对于这种大规模文档，已经涌现了很多相似性度量技术。例如，文献[1-3]提出的minwise哈希算法，是一种较成熟、性能稳定的文档相似性检测技术。最小哈希算法把求解集合的交集问题，转换为一个事件发生的概率问题。利用大量的实验，来对文档的相似性进行估计。该方法，后来被推广到很多的应用领域，包括：Web重复检测[4]、协同过滤[5]、关联规则学习[6]等。

常规的最小哈希算法，利用32位或64位去存储每一个哈希值。然而，当数据规模很大时，这将承受巨大的存储压力。为了解决此困境，文献[7-10]提出了一种空间高效的b位最小哈希算法(b-bit minwise hashing)，该方法只存储最小哈希值的最低b位(b=1, 2, 3,…)。虽然上述方法大大降低了存储空间，但是也牺牲了一定的精度。为此，本文提出一种ES_SSE方法，该方法在原始最小哈希函数的基础上，采用压缩的n位二进制编码，不仅在空间需求上大大降低，而且性能也大大改善。

1 方法概述

文献[7-10]等的大量研究，都是基于这样一个直观认识：来自于不同的两个集合中的元素，如果他们的哈希值相等，则两个哈希值的最低b位肯定相等；如果他们的哈希值不同，则两个哈希值的最低b位以1-1/2b概率不相等。因此，在精度要求不是特别严格的情况下，可以采用空间高效的b位哈希算法。然而，当精度要求高时，必须探寻更加高效的方法。

图1所示为本文研究所经过的几个阶段，即首先对数据源进行预处理，比如shingling文档，去除shingling文档后得到集合中的重复值等。接着，对集合中的每个元素计算最小哈希值(这一步与其他的普通最小哈希方法没有本质的不同)。第三个阶段，为本文研究的核心，即对计算出的每一个哈希值，进行如图2所示的处理。最后一步即对相似性进行估计。

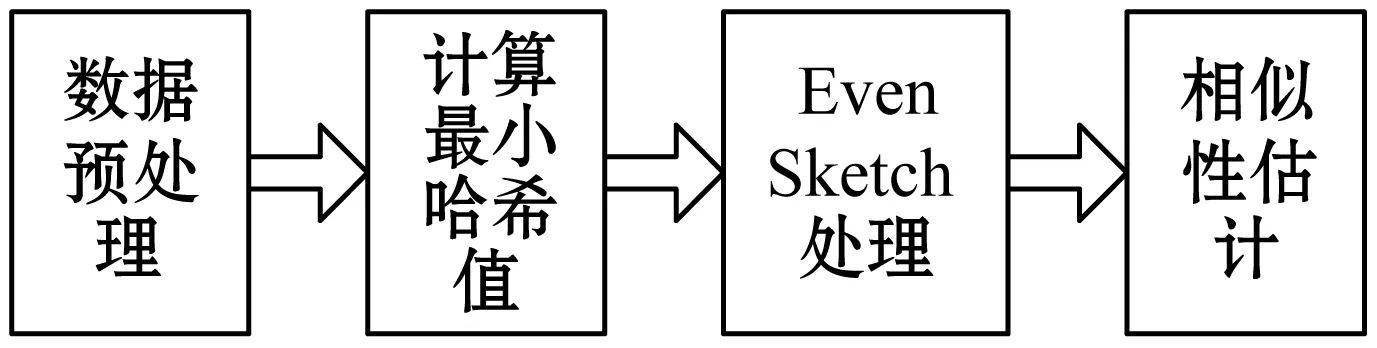
图1 ES_SSE处理流程图

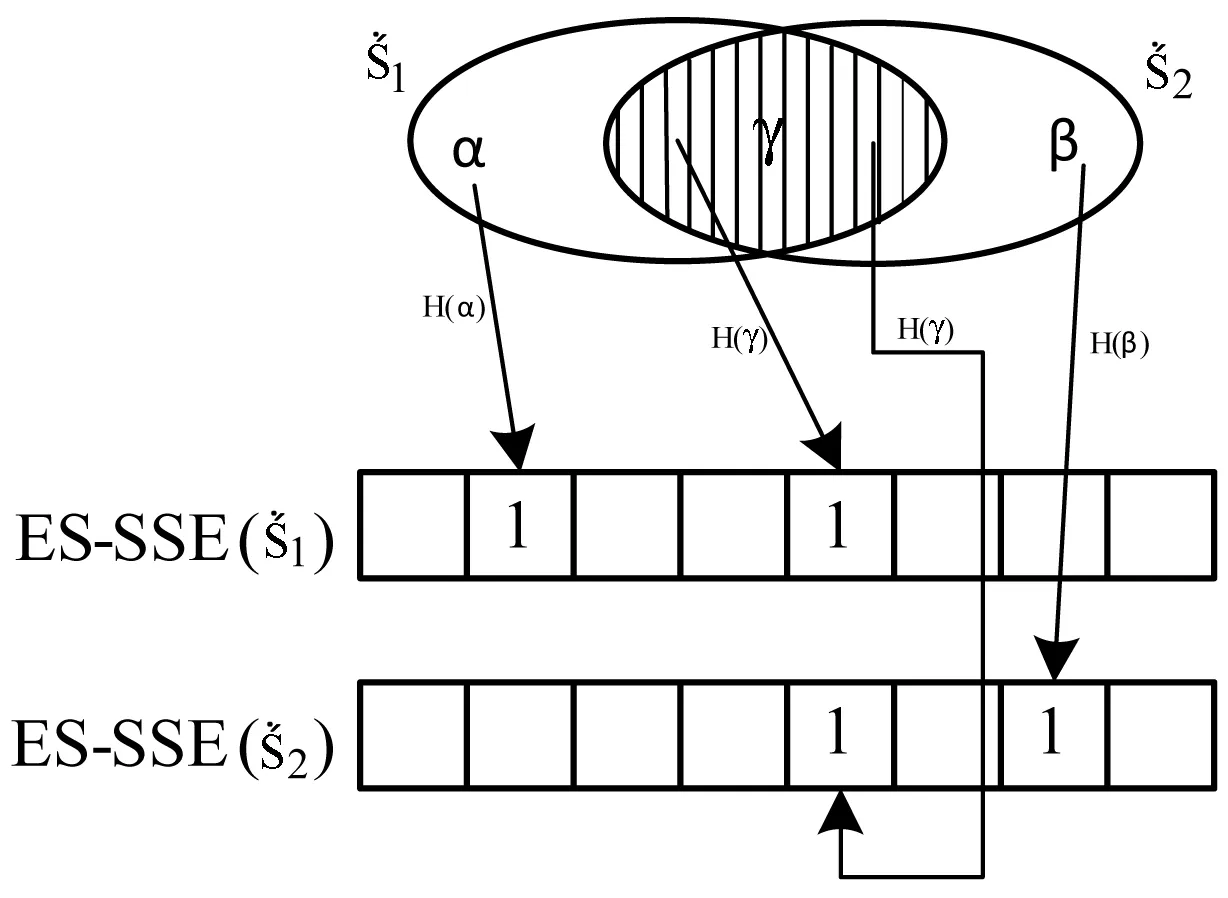
图2 ES_SSE构造示意图

图3描述了b位最小哈希算法的实现过程，如图3所示，对于给定的两个原始集合S1和S2，图中的阴影交集部分，其哈希值的最低b位相同。

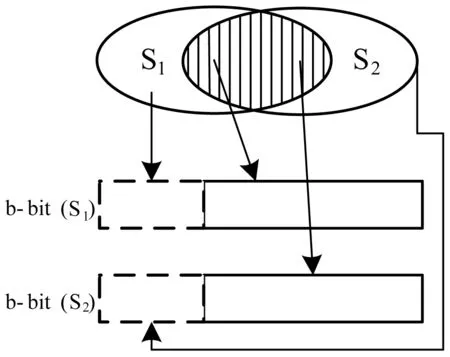
图3 b-bit构造示意图

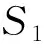
2 模型描述

(1)

li为所有哈希到第i个位置的元素个数的奇偶性。采用此方法，特别是处理海量数据集时，能够大大降低存储空间，因为只判断哈希到某个位置元素个数的奇偶性，大大压缩了空间；然后利用二进制位的异或运算，消除相同的公共部分，只保留记忆了原始集合差异性的部分，进一步降低了存储空间。图1中，进行了两次哈希处理，本文通过对第二次哈希后的集合进行杰卡德相似性估计，反过来会推出原始集合的相似性。

2.1 从ES_SSE估计集合的基数

本小节介绍如何从ES_SSE估计集合的基数。假定用n位二进制位来存储ES_SSE，m表示集合的基数。由图2可以看出，求解ES_SSE的过程，其实可以当作一个投票问题。ES_SSE的构造过程，相当于m个选民对n个候选人进行投票，每次投票后对候选人的票数进行统计，并算出每个候选人所得票数的奇偶性，即求出li。反过来，当得知了ES_SSE向量值，可以对集合的基数进行估计。本文把ES_SSE向量每位的奇偶性当作一个简单双态马尔可夫链模型，即两状态分别对应奇数和偶数，状态变化概率为1/n。当i个选民行使了自己的选举权以后，假定任何一个候选人所拥有的票数为偶素的概率为pi，基于马尔可夫链的简单推导，可以得到以下等式：

(2)

实际上，如果用一个0-1变量Xi表示m个选民投票后，第i个候选人所得票数的奇偶性(Xi为1，表示所得票数为偶数，否则为奇数)，假设X=∑iXi，通过推导则有：

(3)

(4)

因此得出:

(5)

2.2 从ES_SSE估计Jaccard similarity系数

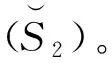
(6)

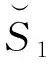
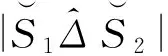
(7)

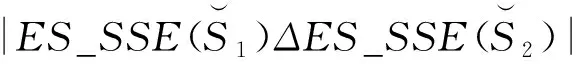
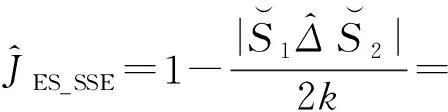
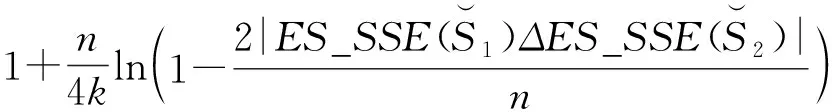
(8)

在文献[11]中，也探讨了跟本文类似的估计问题，其解决的是一个将m个球扔进n个箱子的问题，并利用标准近似泊松分布进行建模，分析了数据的集中性(即数据分布在其均值的周围)和方差区间。本文对此相关问题不作进一步讨论。

3 实验结果及分析

本节将通过实验，验证本文所提出的模型性能。本文实验以处理器Intel(R)Core(TM)i5 CPU(3.30 GHz)，4 GB内存，64位Win7操作系统为实验环境。所有实验在Matlab中进行，为了减小误差，所有实验都是重复10次并取均值。

3.1 参数设置

本文对ES_SSE和b-bit进行对比。正如在文献[9]中讨论的结果，b-bit的性能要依赖于用在原始最小哈希函数上的独立排列的数目。ES_SSE也是基于原始最小哈希函数进行构造的，因此，它也要依赖于独立排列的数目。如果总存储空间为SS位，每个排列的位数为b(b≥1)位，则一共有kb=SS/b个排列。从后面实验可以看出，kb越大，实验精度越高。

在ES_SSE实验中，独立排列的数目kES_SSE由每个ES_SSE向量大小和设置的相似度阈值J0决定，一般情况下，只对那些J>J0的集合对感兴趣。同kb，kES_SSE也是尽量越大越好，来减少图1中两次哈希所造成的误差。选取一个最理想的kES_SSE值将非常困难。不过通过后面的实验，本文得出：如果两个ES_SSE向量具有相似度J0，它们异或后为1的位数占总位数大约31%时，实验将获得最小方差。

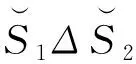
3.2 实验结果

图4 MSE比较实验：J=0.9,n=500-1 000

图5 MSE比较实验：n=750,J=0.75-0.95

图6 ES_SSE和b-bit比较实验:n=512

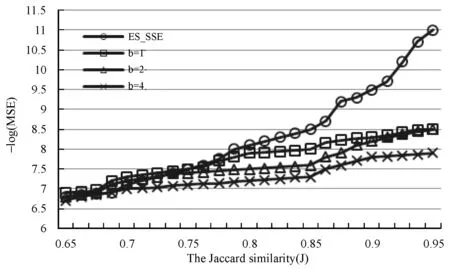
图7 ES_SSE和b-bit比较实验:n=1 024

4 结 语

本文提出了一种压缩二进制方法ES_SSE来对集合间的杰卡德相似系数进行估计。在原始最小哈希函数的基础上，通过再次哈希，利用哈希到某个位置上的元素个数的偶数性，并进行ES_SSE向量之间的异或运算，最后通过模型对原始集合的相似性进行估计。ES_SSE算法大大节约了存储空间，尤其适用于相似度高的场景。实验也验证了本文模型和算法的性能。