基于精细模型的视频车辆三维姿态估计

徐 亮 肖 晶 王中元

(武汉大学计算机学院 湖北 武汉 430072)

0 引 言

随着智能交通系统的不断发展，对监控视频的自动化处理要求也越来越高。监控视频中，行驶车辆是重点关注对象之一。准确地估计车辆的三维姿态参数是监控视频自动化处理的基础，可广泛应用于交通监控、道路执法、安全保障，以及监控视频压缩处理等领域[1]。监控视频中车辆姿态估计的难点在于图像数据在采集过程中丢失了三维世界中的深度信息，并且监控环境下的图像质量较低，大量细节信息得不到保障。因此，仅利用单幅图像包含的信息难以恢复出物体的三维姿态参数。为了准确地理解图像内容，恢复丢失的深度信息。需要借助先验知识，如车辆的三维模型，来估计车辆三维姿态参数[2-3]。

目前，从图像中恢复目标三维姿态参数的方法主要分为如下四类：文献[4]提出一种基于简单线框模型的车辆姿态估计方法。该方法使用几条简单线框表示车辆的三维模型，并利用线框模型与图像中车辆轮廓的匹配误差来评价姿态参数准确性，通过演化算法优化姿态参数使匹配误差不断减小，从而得到最终的位置姿态参数。该方法计算复杂度较低，但简单线框模型难以精确表示真实车辆，因此参数估计精度不高。文献[5-8]提出基于深度学习的目标三维姿态估计方法。该类方法首先通过目标三维模型渲染出各种不同姿态下的图像，以图像-姿态参数对作为训练数据训练卷积神经网络，在进行目标姿态估计时，将测试图像作为网络输入，输出即为对应姿态参数。这种基于图像识别的方法由于不存在严格的投影关系方程，因此很难得到目标姿态参数的准确估计值。文献[9-10]提出基于深度相机的姿态估计方法，该类方法通过深度相机来采集图像及图像的深度信息用于估计目标姿态。相比仅利用图像数据的方法，该类方法能有更好的表现，但是该方法应用场景有限，而且硬件成本很高，不适合应用在监控场景下。文献[11]提出一种基于目标掩码区域的姿态估计方法，该方法首先利用目标颜色直方图信息估计出目标所在区域的掩码图，接着提取目标和模型的外围轮廓，通过最小化两个外轮廓误差来优化姿态参数。该方法是目前姿态估计领域综合效果最好的方法之一，但是由于仅利用了目标的外围轮廓，没有充分利用到目标内部的轮廓信息，使得在目标被遮挡及光照复杂的情况不够鲁棒。

针对上述方法姿态参数估计精度不高、在复杂环境下鲁棒性差等问题，本文提出了一种基于精细模型的车辆姿态估计方法，主要创新如下：1) 相比文献[11]仅利用车辆外轮廓，本文利用到了车辆模型的内外全部轮廓，更多特征的利用可以帮助提升估计结果的准确性和鲁棒性；2) 由于曲线轮廓间匹配复杂且精度低，本文将模型车辆曲线轮廓用分段直线拟合再与真实车辆轮廓匹配，直线化后的轮廓不仅保留了曲线轮廓的边缘信息而且简单有序，能更加充分利用到轮廓的局部特性；3) 采用高斯牛顿算法优化姿态参数，相比文献[11]中梯度下降法需要更少的迭代次数，从而提升方法的实用性。实验结果表明轮廓特征的充分利用能够估计到更加准确的姿态参数，并且在复杂环境下具有很好的鲁棒性。

1 车辆姿态估计原理

车辆姿态估计是利用车辆的三维模型从二维图像中恢复出车辆的三维姿态信息，可以看作是相机成像过程的反演。相机成像过程如下式所示：

λm=K[R|t]M

(1)

式中：λ是尺度因子，m=[u,v,1]T是图像中像素点的齐次坐标，M=[xm,ym,zm，1]T是模型三维点的齐次坐标。K是3×3的相机内参矩阵，每个相机的内参矩阵是固定的，可以提前标定好，本文中假定K是已知的。[R|t]是模型相对相机的外参矩阵，R是3×3的旋转矩阵，由罗德里格斯变换可以转化成3×1的欧拉旋转角r，t是3×1的位置平移向量。

姿态估计问题就是利用式(1)的投影关系，求解旋转角r和平移向量t的过程，包含6个未知变量。该过程包含两个子问题：首先需要建立二维图像特征与三维模型特征的对应关系。其次是根据建立的对应关系，利用投影方程求解出姿态参数。而实际中由于目标图像复杂且往往存在噪声，很难直接建立二维图像特征与三维模型特征的准确对应关系[12]。因此估计姿态时通常将这两个问题耦合在一起：利用特征匹配构建一个能量函数来衡量当前状态下姿态参数准确性，再从初始值出发，优化姿态参数最小化能量函数，从而得到最终收敛的姿态参数，即将姿态估计问题转化成一个最优化问题以便于求解。

如上所述在一般情况下，姿态参数有6个未知变量。考虑到实际情况中车辆一般是在地平面上行驶，车辆姿态相对相机只有3个自由度，即相对地面位置X、Y及在地面上的旋转角度θ。引入地平面约束后，需要求解的未知变量减少到了3个，求解时能够减少搜索空间，更易于收敛到准确姿态。前提是需要先标定好地平面与相机间的外参矩阵P，投影方程便可简化成下式：

(2)

记p=[X,Y,θ]，即为待求的车辆相对地面的姿态参数。

2 基于精细模型的车辆姿态估计方法

本文方法的整体流程图如图1所示。对输入图像，首先从中检测车辆，粗略估计车辆的位置和旋转角作为初始化姿态参数，利用初始姿态及标定好的相机参数将车辆三维模型投影到图像上。接着提取投影区域的边缘轮廓，并采用直线拟合，得到模型的直线化轮廓。再计算模型车辆轮廓与真实车辆轮廓间的匹配误差，采用高斯牛顿优化算法最小化匹配误差，直到匹配误差小于设定的阈值即停止优化，从而求得最终姿态参数。

图1 本文方法流程图

2.1 姿态参数初始化

基于模型的车辆姿态估计方法，需要首先确定视频第一帧图像中车辆初始姿态参数，后续图像可以采用前一帧求得的姿态参数作为初始值。初始化结果的好坏对整个过程有重要影响，一个好的初始值通常会更容易收敛到最优解。文献[11]采用人工手动的方式来初始化位置姿态参数。这种方式繁琐低效，在很多场合都不适用。本文利用车辆区域在图像中位置以及车辆梯度信息对姿态参数初始化。首先检测出图像中车辆的外接矩形框，关于车辆检测方法在文献[13]中有详细论述。粗略假定矩形框的中心即为模型中心的投影点，利用式(2)可以确定车辆模型中心相对地面的位置坐标，以此作为初始化位置参数(X0，Y0)。另外，根据车辆的结构特点，图像中车辆的梯度方向大多分布于车辆模型坐标系的x轴和y轴。通过提取前景车辆的HOG特征可以检测到这两个方向，计算出它们的夹角，并结合投影方程可以初步确定车辆相对Z轴的旋转角θ0[4]。综合位置参数和旋转角参数可以得到初始姿态参数p0=(X0,Y0,θ0)。

2.2 轮廓提取和匹配

2.2.1 车辆轮廓提取

由于车辆包含丰富的轮廓信息，通常采用轮廓特征来建立二维特征与三维特征的匹配关系。首先利用当前状态下姿态参数，根据式(2)投影方程将精细车辆模型渲染到图像平面上，再采用Canny边缘检测算子分别提取真实车辆轮廓和模型车辆轮廓，如图2所示。

(a) 真实车辆(b)真实车辆轮廓

(c) 模型车辆(d) 模型车辆轮廓 图2 车辆轮廓

2.2.2 模型车辆轮廓直线拟合

从图2(b)-(d)中可以看到真实车辆轮廓和模型车辆轮廓都是由杂乱无规律的曲线组成，曲线间的匹配需要提取曲线的特征量，包括曲率角、弧长弦长比、区域面积比等[14]，这些特征量的提取和匹配需要大量计算，加之图像轮廓中噪声的干扰，使得曲线匹配过程变得更加复杂困难。相比之下，直线轮廓间的匹配要显得简单准确，考虑到车辆自身的刚性结构特点决定了其轮廓包含丰富的直线信息，可以将曲线轮廓看作是多段很短直线的拟合。同时，在轮廓匹配过程中，分段直线能更加突显出轮廓的局部特性[15]。因此本文采用分段直线来逼近模型车辆的曲线轮廓，再与真实车辆轮廓匹配。

随机抽样一致性算法(RANSAC)是一种常用的鲁棒估计算法，常被用于在有噪声的数据中拟合出最佳的直线。本文采用改进的 RANSAC算法来完成曲线轮廓直线拟合的过程，详细过程如下：

输入：一幅轮廓图；

输出：轮廓拟合后的若干条直线。

步骤1随机选择起始点：在现有轮廓点中先随机选择一点(x0，y0)，在以该点为中心边长为10个像素点的正方形框内搜索其他轮廓点,并保存。

步骤2初步拟合直线：利用搜索到的轮廓点，逐个与(x0，y0)组成直线，计算其他轮廓点到直线的距离，设定阈值T，距离小于T的轮廓点判定在该直线的附近，统计每条直线附近轮廓点的个数。附近轮廓点最多的直线作为初步选定的直线，保存该直线方向。

步骤3扩大搜索范围：同样以(x0，y0)为中心，在边长为100个像素点的正方形框内搜索其他轮廓点,并保存。

步骤4确定最终拟合直线：计算搜索到的每个轮廓点到初步选定直线的距离，保存所有距离小于T的轮廓点。沿着直线方向，从保存的轮廓点中找到两个端点，端点连线即为拟合的直线轮廓。

步骤5删除已经拟合轮廓点：删除选定直线附近的轮廓点，若剩下的轮廓点数小于设定的阈值，则保存所有分段直线并退出。

步骤6迭代：返回步骤1。

该方法能高效地用直线来拟合投影车辆的轮廓。直线拟合后，复杂零散的曲线轮廓变成了简单结构化的直线轮廓。其中距离阈值T与拟合准确度、拟合直线条数n有关。拟合结果见图3。

(a) T=1 pix，n=392 (b) T=2 pix，n=244

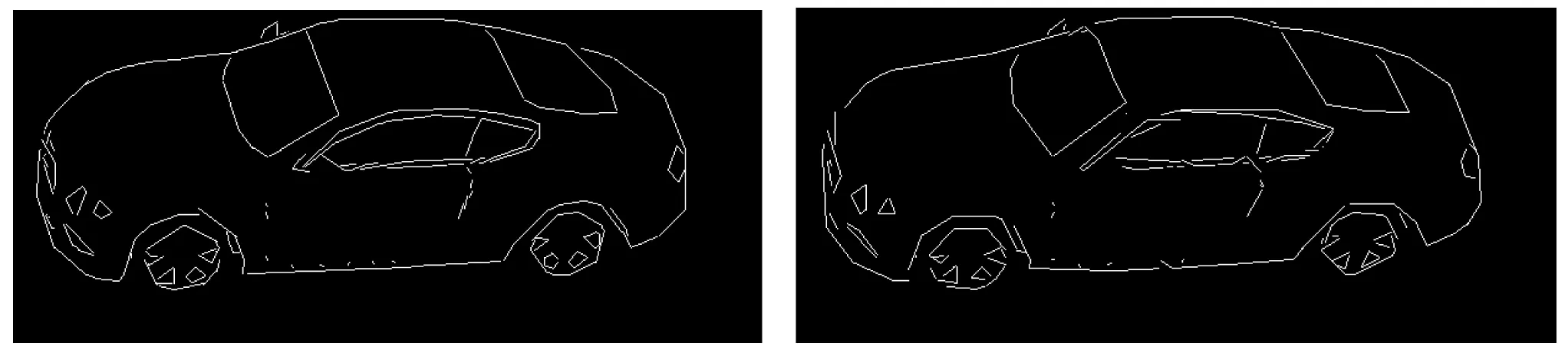
(c) T=3 pix，n=214 (d) T=4 pix，n=182

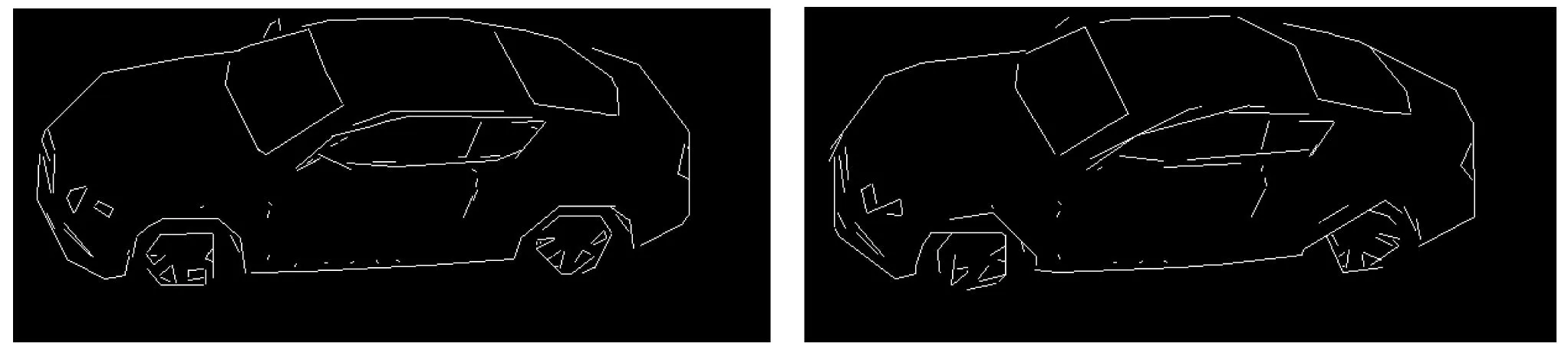
(d) T=5 pix，n=150 (e) T=6 pix，n=125 图3 直线拟合曲线轮廓

从图3中可以看到，阈值T越小，轮廓拟合越精确，直线条数也越多；相反，阈值T越大，轮廓拟合越粗糙，直线条数也越少。当T=3个像素及以上时模型已经开始出现不同程度失真。T=2个像素，模型拟合精确同时直线条数相对最少，本文姿态估计实验选择该阈值。

2.2.3 轮廓匹配

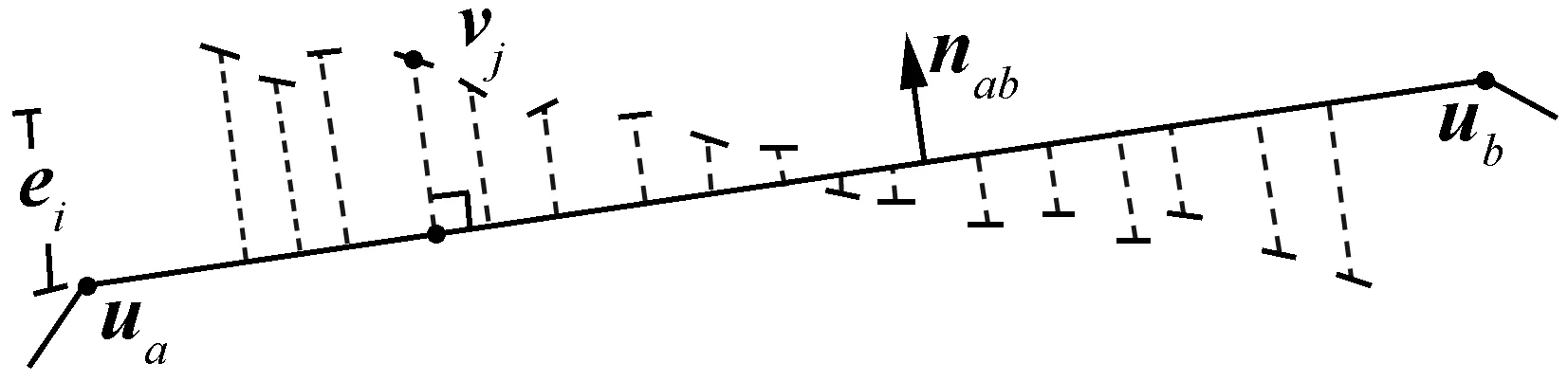
图4 轮廓匹配示意图

模型轮廓用分段直线拟合后便只需要比较每段直线轮廓与真实车辆轮廓间的匹配误差，再将所有直线的匹配误差累加得到当前姿态下轮廓匹配误差。对于每一段模型直线轮廓，沿着其法线方向在固定长度内搜索真实车辆的轮廓点，然后计算搜索到的每一个真实车辆轮廓点到直线轮廓的垂直距离。如图4所示，ua、ub是直线轮廓的两个端点，虚线是在其周围搜索到的真实车辆轮廓点，nab是直线法向量，vj是直线周围第j个真实车辆轮廓点。该段直线周围所有真实车辆轮廓点到直线垂直距离的和即为该条直线轮廓的匹配误差ei：

(3)

所有分段直线的匹配误差构成当前姿态参数下的能量函数e=[e1,e2,…,en]。

2.3 优化过程

在定义了轮廓间匹配误差后，轮廓匹配问题就转化成了一个非线性最优化问题，优化目标是最小化能量函数，即mine(p)。通过不断地优化姿态参数来减少匹配误差，投影轮廓和图像轮廓也就不断地靠近，最终收敛到准确的姿态参数。不同于文献[11]的梯度下降优化方法，本文采用高斯牛顿法来优化目标函数，相比梯度下降法需要更少的迭代次数。优化过程是从初始姿态p0开始，根据当前状态的匹配误差计算出下一状态的参数增量：

pi+1=pi+Δi

(4)

式中：Δi是第i次迭代增量，高斯牛顿法是通过最小化第i+1次的目标函数来计算Δi的取值。对第i+1次误差采用一阶泰勒展开：

e(pi+Δi)≈e(pi)+JΔi

(5)

式中：J是目标函数e对姿态参数p的雅克比矩阵，Jij=∂ei/∂pj，Jij反映了第j个姿态参数的变化对第i条直线轮廓匹配误差的影响。通过最小化‖e(pi)+JΔi‖来计算Δi，即：

Δi=arg min‖e(pi)+JΔi‖

(6)

利用最小二乘法可以求得：

Δi=-(JTJ)-1JTei

(7)

从初始值开始，利用上述迭代方法不断更新姿态参数，直到匹配误差小于设定阈值，即认为收敛到最终姿态。

3 实验结果

为了验证本文提出的采用分段直线拟合模型轮廓与真实车辆轮廓匹配，再结合高斯牛顿法优化姿态参数方法的效果，在模拟监控系统的沙盘平台上进行了仿真实验。沙盘平台大小是3 m×5 m，上面有车辆行驶，车身长度是120 mm。沙盘上布置有多个1080p的高清监控摄像机。利用采集的监控视频作为实验数据源，车辆的三维模型通过激光扫描方法获得。实验数据处理在Visual Studio 2010环境下，并利用了OpenCV、OpenGL开源库。

姿态参数估计结果的评价指标主要包括估计值相对真实解的准确性、在复杂环境下能否准确收敛的鲁棒性。下面将从准确性、鲁棒性两个方面来验证本文方法的性能，并将文献[4-5，11]作为对比方法进行对比分析。

3.1 姿态估计准确性

对监控摄像机采集到的一段视频，首先利用沙盘平台的CAD模型图人工标定出每一帧车辆的真实姿态pE=(XE,YE,θE)。再分别采用本文方法、文献[4]中基于简单线框模型的方法 、文献[5]中基于深度学习的方法和文献[11]中基于目标外轮廓的方法求解每帧姿态，记求解出的姿态参数为(X*,Y*,θ*)。姿态估计的准确性包括平移误差ET和旋转角度误差ER。

(8)

测试结果如图5所示。

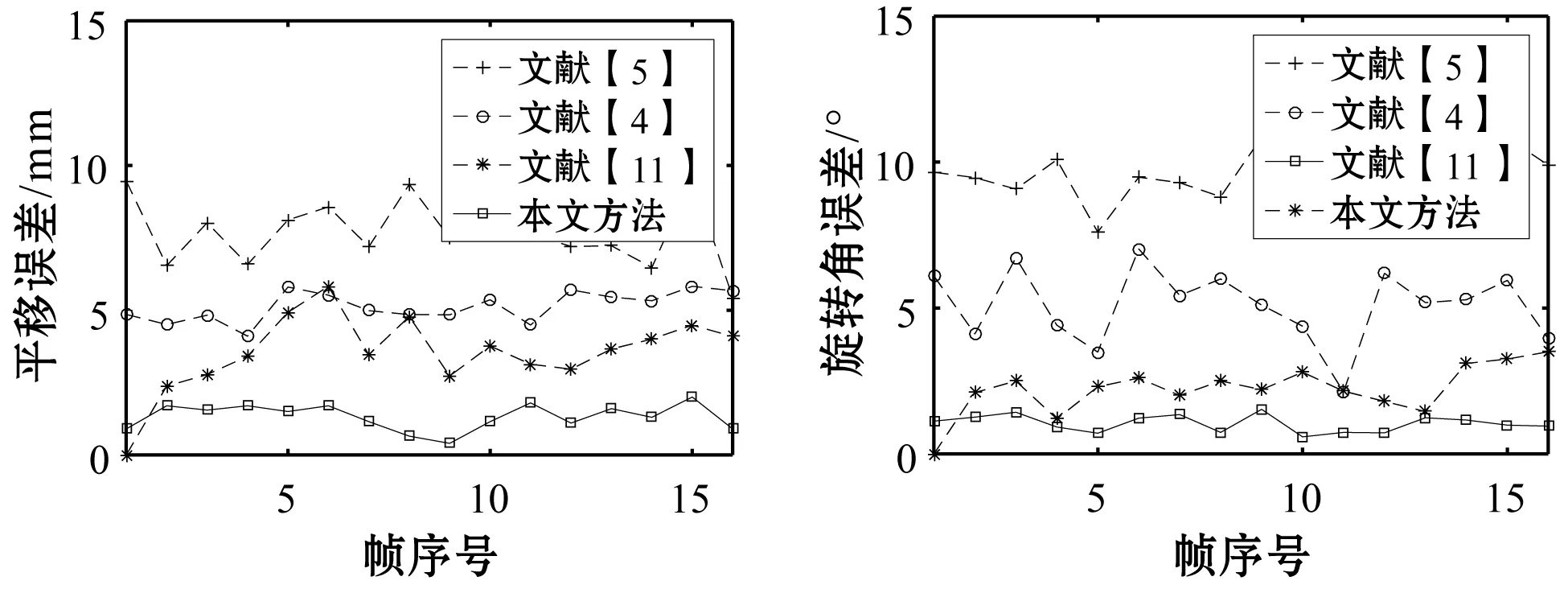
(a) 平移误差 (b) 旋转角误差 图5 姿态误差对比图

在测试的16帧图像中，本文方法在X轴和Y轴的平移误差平均为1.32 mm，占车身总长度的1.10%，旋转角度误差平均为1.04度；而文献[4]平移误差平均为5.13 mm，占车身总长度的4.28%，旋转角度误差平均为5.64度；文献[5]平移误差平均为7.98 mm，占车身总长度的6.65%，旋转角度误差平均为9.63度；文献[11]平移误差平均为3.75 mm，占车身总长度的3.13%，旋转角度误差平均为2.25度。图5中的实验结果说明本文方法估计出的车辆平移参数和旋转角度相较于对比方法都更加准确稳定。

3.2 姿态估计鲁棒性

验证本文方法在复杂环境下能否准确求解出姿态参数，从四个方面进行验证：差的初始值、车辆转弯、车辆遮挡、复杂光照环境。测试结果如图6所示。

(a) 差的初始值 (b) 车辆转弯

(c) 车辆遮挡 (d) 复杂光照 图6 本文方法鲁棒性验证

为便于显示将收敛后的结果放大，图6中车身上的白色轮廓是姿态参数收敛后模型车辆的轮廓，图6实验结果表明模型车辆轮廓与真实车辆轮廓匹配准确，误差很小。表1和表2展示了本文方法与对比方法在复杂环境下求得姿态参数的平移误差与旋转角度误差。分析表中数据可知，文献[4-5，11]在复杂环境下平移误差占车身比的平均值分别增大3.10%、4.61%、2.49%，旋转误差平均值分别增大2.13°、5.66°、2.76°，部分环境下甚至出现了不能收敛的情况；而本文方法在复杂环境下平移误差占车身比平均值仅增大0.38%，旋转误差平均值仅增大0.32°，相对一般环境姿态参数估计精度并没有明显下降。所以即使在复杂环境下利用本文方法也能准确估计出车辆的姿态参数，证明本文方法具有很好的鲁棒性。

表1 复杂环境下平移误差对比(占车身总长百分比) %

表2 复杂环境下旋转误差(度)对比

实验结果证明，所提出方法姿态估计准确性有明显改善，在复杂监控环境下也能表现出很好鲁棒性。

4 结 语

本文针对监控场景下由于环境复杂、图像质量低，从监控视频中恢复车辆三维姿态变得困难的问题，提出了一种基于精细模型的车辆姿态估计方法。通过模型车辆轮廓与真实车辆轮廓的匹配误差构建能量函数来衡量姿态参数的准确性，为充分利用轮廓信息的局部特性，采用改进的RANSAC算法将模型车辆曲线轮廓用分段直线拟合再与真实车辆匹配，最后采用高斯牛顿优化算法最小化匹配误差，得到最终姿态参数。实验结果表明，本文方法姿态参数估计结果的准确性和稳定性相较目前方法有明显改善，在复杂环境下能准确地恢复出车辆姿态参数，具有很好的鲁棒性。