基于节点中心性和社区相似性的快速标签传播算法

顾军华 ，霍士杰，王守彬，田 喆

(1．河北工业大学计算机科学与软件学院，天津300401; 2．河北省大数据实验室(河北工业大学)，天津300401)(*通信作者电子邮箱jhgu_hebut@163．com)

0 引言

自然界与人类社会中的许多系统都可以用复杂网络模型表示，网络社区结构是复杂网络中最普遍和最重要的拓扑属性。社区发现算法可以通过分析网络中节点之间的关联性，挖掘复杂网络中的社区结构，从而揭示复杂网络中隐含的特性和功能，对于网络结构的理论研究和网络分析的实际应用有着重要的作用。

2007年 Raghavan等［1］首次将标签传播算法(Label Propagation Algorithm，LPA)应用于社区发现。与传统的社区发现方法(基于层次聚类的算法［2－3］、基于随机游走的算法［4］等)相比，LPA仅依赖于网络的传播特性，且具有线性的时间复杂度，适合用于对复杂网络进行社区发现和分析的优点。但是LPA也有一些缺点:1)节点更新顺序具有随机性，并且当邻接节点中出现次数最多的标签(最大值标签)有多个时，会随机选择一个标签;2)存在不必要的标签更新过程;3)更新标签时仅仅考虑邻接节点中标签出现的次数，忽略邻接节点的局部结构信息。这些缺点会导致算法延迟收敛，社区发现的结果准确率低且稳定性差的问题。针对以上问题，2014年，Xing等［5］提出了基于节点影响力的标签传播算法(Node Influence Based Label Propagation Algorithm for community detection in networks，NIBLPA)，该算法使用k-shell分解方法计算每一个节点的影响力值，依据影响力值从高到低的顺序更新标签和选取标签，提高了算法的稳定性和准确率，但是时间复杂度也有所提升。2015年，Sun等［6］提出了基于中心性的标签传播算法(Centrality-based Label Propagation algorithm for community detection in networks，Cen_LP)，该算法为每一个节点定义了节点中心值和节点偏向值，依据节点中心值从低到高的顺序更新标签并且利用节点偏向值选取标签，算法在不增加时间复杂度的情况下，提高了社区发现的准确率。2017年，Ma等［7］提出了基于节点重要性和随机游走的标签传播算法(An improved Label Propagation Algorithm based on Node Importance and random walk for community detection，NILPA)，该算法依据节点的度数计算节点重要性，并且依据随机游走理论形成节点相似度矩阵，在两者的基础上形成新的度量标准来衡量节点之间的紧密程度，依据该度量标准更新标签。算法提高了社区发现的准确率，但由于计算节点相似性依赖于矩阵相乘，在网络规模不断扩大时，会消耗越来越多计算资源，而且时间复杂度也较高。综上所述，尽管上述算法在准确率上有所提高，但是都提高了算法的时间复杂度，降低了算法的执行速度。

为了在加快算法的执行速度的基础上提高算法准确率和稳定性，本文提出了基于节点中心性和社区相似性的快速标签传播算法(Fast Label Propagation Algorithm based on the Node Centrality and Community Similarity，FNCS_LPA)。FNCS_LPA首先计算每一个节点的中心性度量值，按照中心性度量值从低到高的顺序排序并加入到节点信息列表中，用节点信息列表指导更新过程，通过记录节点信息列表中每一个节点的状态信息，判断当前节点是否需要更新，从而避免了不必要的更新，提高了运行速度。在更新过程中，FNCS_LPA利用基于社区相似性的更新规则，即不仅仅考虑邻接节点中标签出现的次数，还会评估每个邻接节点与待更新节点的相似性，社区相似性依赖于节点相似性求和，待更新节点会选择社区相似性最高的社区，从而提高算法的准确率。

1 基于节点中心性的快速标签传播算法

1．1 基于节点中心性的更新顺序

在LPA的每一次迭代过程中，节点的更新顺序是随机的，这等同于平等对待网络中的所有节点。事实上，网络中的每个节点的重要程度依赖于其在网络中的局部信息，并不是同等的，如果平等对待，按随机的顺序更新标签，可能会造成结果与实际不符，导致算法准确率低且稳定性差的问题。基于此，本文提出了基于节点中心性的更新顺序，其中，节点中心性依赖于节点的聚集系数(Clustering Coefficient)和节点密度。假设节点i和节点j是网络中的两个节点。

定义1 节点的聚集系数。节点i的聚集系数定义如下:

其中:Ni表示节点i的邻接节点集合，|Ni|表示节点i的邻接节点数，E(i)表示节点i的邻接点之间实际的连边数。节点的聚集系数可表示为当前节点的所有邻节点之间实际连边数与所有可能连边数的比值，由于节点的邻接点之间实际存在的边不会大于可能存在的最大值，因此节点的聚集系数的取值范围在0～1:当节点的度数为0或1时，或者当节点的邻接点之间相互独立时，该节点的聚集系数为0;当节点的聚集系数为1时，则表示该节点与其邻接点之间构成完全图。因此节点的聚集系数越高，说明节点具有越高的聚集度。

定义2 节点密度。节点i的密度定义如下:

定义3 节点中心性度量值。

节点中心性度量值表示为节点密度和节点聚集系数的乘积，δi的值越大，表明节点在网络中的重要程度越高。在实际生活中，重要程度高的节点为专家，而重要程度低的节点为普通求知者，普通求知者都是听取专家的知识，从而完成知识传播。同样，在标签传播过程中，标签就是知识，节点就是人，重要程度低的节点往往要先采纳周围重要程度高的节点的标签，从而完成标签传播。因此，节点δi的值越小，该节点就越先更新标签，这样得到的结果才会与实际相符，因此节点的更新顺序按照节点中心性度量值升序更新。

1．2 基于节点中心性的快速标签传播算法

LPA运行在线性时间内，具有执行速度快的优点。LPA在前几次迭代过程中节点改变标签的概率是非常高的，但是，在5次迭代以后，95%以上的节点都会被正确地划分(当前节点的标签已经变为邻接节点中最大值标签)。为了说明这一现象，本文将 LPA分别应用在 CA-Hepth、CA-GrQc、Email和PGP这4种常用的真实网络数据集上进行社区发现，本文实验将每一个真实网络都看作无向无权图，每一个图都没有自循环的边并且只取图的最大连通子图。本文所有的实验均使用Python语言实现，在 Window 7，AMD Core A8-4555 CPU 1．6 GHz，8 GB 内存环境下进行。

1．2．1 实验一:LPA的收敛性

数据集详细信息如表1所示，计算5次迭代以后已被正确划分的节点占总节点的百分比。每个网络重复100次实验，4种网络的收敛信息如表2所示。

表1 第一部分数据集介绍Tab．1 Introduction of the first part datasets

表2 网络的收敛信息Tab．2 Convergence information of networks

从表2可以看出，在5次迭代以后，Email网络有96．64%的节点被正确划分，CA-Hepth网络有98．97%的节点被正确划分，Email和PGP网络有99%以上的节点都已被正确划分。这说明无论总的迭代次数是多少，LPA在5次迭代以后，95%以上的节点都已经得到了正确的划分，而5次迭代后的每一次迭代，仅仅较少的节点标签会发生改变，而对于大部分的节点来说，即使更新标签，也不会改变标签，这些不必要的更新拖慢了算法的收敛速度。针对这一问题，本节提出基于节点中心性的快速标签传播算法。

1．2．2 实验二:LPA与FNC_LPA的对比

LPA在每次迭代过程中，对节点标签的更新有两种情况:一种是邻接节点中的最大值的标签只有一个，另一种是邻接节点中的最大值标签有多个。如果当前节点的标签已经是邻接节点中的唯一最大值标签，这样的节点称为被动节点，被动节点在本次更新中不会再改变标签;如果邻接节点中的最大值标签有多个，当前节点的标签是其中之一，这样的节点称为干扰节点，根据LPA的更新规则，干扰节点会随机选择其中一个标签，干扰节点在本次更新中可能会改变标签。被动节点和干扰节点以外的其他节点是主动节点，主动节点在本次更新中一定会改变标签。如果能避免对被动节点的标签更新，算法会以更快的速度收敛，因此，本文构建一个节点信息列表，其中包含所有的节点和每个节点的状态信息(被动、干扰和主动)。每次只选择信息列表中的干扰和主动节点进行标签更新，标签更新完成后再进行状态更新。

基于节点中心性的快速标签传播算法(Fast Label Propagation Algorithm based on Node Centrality，FNC_LPA)的具体流程如下:

第一步 按照式(1)、式(2)和式(3)计算节点的中心性度量值，将所有的节点按照节点中心性度量值降序排序并加入节点信息列表当中。每一个节点都被初始化为一个独一无二的标签，都被设置为主动节点。

第二步 从节点信息列表中随机选择一个主动节点或干扰节点，按照节点标签更新规则，对当前节点的标签进行更新。标签更新完成后对该节点及其邻接节点进行状态更新，节点在更新状态时，可能会更新为被动节点、主动节点和干扰节点。

第三步 根据节点状态判断节点信息列表中是否还有主动节点:若有，继续执行第二步;否则，算法结束。

为了评估FNC_LPA的有效性，本次实验包括表1和表3中的8个真实网络数据集。对8种数据集分别使用FNC_LPA和LPA进行社区发现，对比算法收敛时所需的迭代次数和模块度［11］。模块度是一种比较重要的衡量网络社区结构强度的方法，计算公式如下:

其中:Lc表示社区c内部的链接数，m表示整个网络边的总个数，Dc表示社区c内部节点的度数总和，L表示整个网络的全部社区。

表3 第二部分数据集介绍Tab．3 Introduction of the second part datasets

表4 LPA和FNC_LPA平均模块度对比Tab．4 Comparison of average modularity between LPA and FNC_LPA

为了使算法具有可比性，FNC_LPA与LPA使用相同的更新规则(当前节点的标签选取邻接节点中的最大值标签)。FNC_LPA的迭代次数记为算法总更新次数和节点总个数的比值。模块度和迭代次数为对每一个网络重复100次实验后所求得的平均值，迭代次数对比如图1所示，可以看出，因为FNC_LPA避免了很多不必要的更新，所以迭代次数明显少于LPA。在 karate、dolphins、polbooks和 netscience 网络上，FNC_LPA的迭代次数是LPA的1/5至1/2左右，在Email和CAGrQc网络上，FNC_LPA是LPA的1/6左右，在CA-Hepth和PGP网络上，FNC_LPA是LPA的1/10左右。平均模块度对比如表4所示，可以看出，与 LPA相比，FNC_LPA除了在Email和CA-Hepth网络上模块度有小幅提升以外，在其余网络上模块度几乎没有发生变化。因此，实验结果证明FNC_LPA在没有改变社区发现效果的基础上，能够大幅度降低迭代次数。

图1 FNC_LPA和LPA的迭代次数对比Fig．1 Comparison of iterations between FNC_LPA and LPA

2 基于社区相似性的更新规则

LPA的更新规则仅仅考虑邻接节点的标签出现次数，并且当前节点的标签更新为邻接节点中最大值标签，具有相同标签的节点看作一个社区，这种更新规则默认是将每一个邻接节点与当前节点的相似性(社区相似性依赖于节点相似性求和)看作是相同的，LPA最终是将最大值标签所代表的社区作为与当前节点相似性最高的社区。实际上，每一个邻接节点与当前节点的相似性并不是同等的，如果同等对待，会导致算法准确率低且稳定性差的问题。本章提出基于社区相似性的更新规则，社区相似性是由节点相似性求和得到，其中节点相似性依赖于节点之间的公共节点个数和节点的度数，基于社区相似性的更新规则会使待更新节点选择邻接节点的社区中相似性最高的社区。

本章对算法中使用的主要概念进行形式化定义，如下所示:

定义4 边缘度数比。假设节点i和节点j是图中的两个节点，i与j的边缘度数比定义如下:

其中:sim(i，j)表示节点i和节点j的公共节点的个数，di表示节点i的度。

定义5 节点相似性。节点j对节点i的重要程度定义如下:

其中:c1和c2是取值在0～1的两个常数，ρij是节点i和节点j的边缘度数比。

定义6 社区相似性。节点i与社区l的相似性定义如下:

定义7 近似最大值标签。在LPA中，当前更新的节点的标签选取邻接节点中的最大值标签，将这个标签的出现次数记为max;然而，如果邻接节点某类标签的出现次数(计为n)和max的值相差不大时，这类标签称为近似最大值标签。算法引入一个取值在0～1的常量Radio来衡量近似程度。

若邻接节点中标签出现次数n满足式(8)，都称之为近似最大值标签。正在更新的当前节点也可能选择近似最大值标签，其中，在更新过程中为了不考虑节点数量较少的标签，Radio的值不宜设置过大，应在0～0．5。近似最大值标签的引入，避免了对每一个社区进行相似性计算，提高了算法效率。

定义8 基于社区相似性的更新规则。假设集合T中保存了节点i的邻接节点中的最大值标签(社区)和近似最大值标签，L(i)表示节点i的标签，基于社区相似性的更新规则如式(9)所示:

式(9)是在集合T中，让节点i选择使得S(i，l)最大的一类标签，如果有多类标签使得S(i，l)最大，就从中随机选取。

为了验证该更新规则的有效性，本次实验在LPA中使用基于社区相似性的更新规则形成基于社区相似性的标签传播算法(LabelPropagationAlgorithmbasedonCommunity Similarity，CS_LPA)，CS_LPA的节点更新的顺序是随机的。其中式(6) 中的c1取值1，c2取值0．2，式(8) 中的Radio值取0．4。本次实验除了使用表1和表3中的8种真实网络数据集，还应用了LFR(Lancichinetti Fortunato Radicchi)基准网络。LFR基准程序是由Lancichinetti等［16］提出的专门用于生成模拟网络的算法，该算法主要根据输入的参数，尽可能地生成符合真实网络特征的人工合成网络，因此具有较高的实验价值，是当前社区发现研究中最为常用的模拟数据集。在生成LFR基准网络时常用的参数如表5所示，其中mu表示节点与社区外部连接的概率，其值在0～1，mu值越大，表明社区的结构越不明显，社区发现的难度也越大。本次实验使用的LFR基准网络数据集如表6所示，其中包含4组LFR基准网络，每组包含15个不同 mu值的网络，mu的取值在0．1 ～0．8，间隔为0．05。相比2000S(5000S)网络，2000B(5000B)网络中每一社区内的节点个数较多。

表5 LFR基准网络的主要参数Tab．5 Parameters of LFR benchmark network

表6 LFR基准网络数据集描述Tab．6 Description of LFR benchmark network datasets

归一化互信息(Normal Mutual Information，NMI)［17］能够量化算法对网络进行的划分和网络的真实划分之间的关系，是一种在社区发现领域常用的度量标准。NMI的取值在0～1，其计算式(10)所示:

其中:A是网络的真实划分，B是算法对网络所进行的划分，CA表示A种划分的社区个数，CB表示B种划分的社区个数，N表示一个矩阵，Nij表示A种划分第i个社区中的节点出现在B种划分第j个社区中的节点个数，Ni·表示矩阵N第i行的求和，N·j表示矩阵N第j列的求和。n表示整个网络节点的个数。如果A种划分和B种划分是相同的，则NMI(A，B)的值为1。NMI的值越高，表示算法社区发现的准确率越高。

将CS_LPA和LPA分别用在表1和表3的8种真实网络数据集和4种LFR基准网络数据集上进行社区发现，对每一个网络重复100次实验。在8种真实网络数据集上与LPA对比平均模块度，对比如表7所示:在所用的数据集上，CS_LPA的模块度都比 LPA要高;其中，在 Email、CA-Hepth、dolphins和netscience网络上，CS_LPA模块度有明显的提高。由于LFR基准网络已知真实的划分结果，因此在LFR基准网络数据集上与LPA对比平均NMI值。NMI的对比如图2所示。

图2 LFR基准网络上CS_LPA和LPA的NMI对比Fig．2 NMI comparison of CS_LPA and LPA on LFR benchmark network

从图2(a)可以看出，mu的值在0．1～0．45时，两种算法都能较好地发现社区结构;mu的值在0．45～0．6时，LPA的NMI值迅速下降，表明社区发现的准确率在下降，而CS_LPA的NMI的值远高于LPA;mu的值在0．65～0．8，LPA已无法进行社区发现，而CS_LPA仍可进行。图2(b)产生了类似于图2(a)的效果，mu的值在0．1～0．4时，两种算法都能较好地发现社区结构，而 mu的值在0．45～0．8时，CS_LPA的NMI值高于LPA。在图2(c)和图2(d)中，当 mu大于0．6时，CS_LPA的NMI明显高于LPA。

综上所述，相比LPA，CS_LPA提高了社区发现的准确率，尤其对于社区结构不清晰的网络，算法的优势更加明显。

表7 LPA与CS_LPA平均模块度对比Tab．7 Comparison of average modularity between LPA and CS_LPA

3 FNCS_LPA算法

3．1 算法流程

在第1章和第2章中，本文分别引入了基于节点中心性的快速更新过程和基于社区相似性的更新规则，在基于节点中心性的快速更新过程中引入基于社区相似性的更新规则，形成基于节点中心性和社区相似性的快速标签传播算法(FNCS_LPA)。算法的伪代码如下:

FNCS_LPA:

输入 G(V，E)、c1、c2、Radio;

/*输入图的邻接矩阵和式(6)，式(8)的参数*/

输出 社区划分结果。

1) 为每个节点分配一个独一无二的标签;

2) 按式(1)～(3)计算所有节点的中心性度量值，按照升序的顺序添加到节点信息列表当中，将所有的节点标记为主动节点;

3) 从节点信息列表中随机选取一个主动节点或干扰节点，记为i;

4) 将当前节点i的邻接节点中出现次数最多的标签和近似最大值标签加入集合T当中;

5) 初始化maxLabel集合为空;maxLabel记录与当前节点i相似性最高的一个或多个标签。

6) for each l∈T do

7) maxS←0;

8) 依据式(6)计算S(i，l);

9) if S(i，l)==maxS then

10) 将l标签添加到maxLabel中;

11) else if S(i，l) ＞ maxS then

12) maxS ← S(i，l);

13) 从maxLabel中移除所有元素;

14) 将l标签添加到maxLabel中;

15) end if

16)end for

17)当前节点i从maxLabel集合中随机选取标签;

18)for each j∈N(i)∩ i do

/* 更新当前节点i和i的邻接节点的状态*/

19) if node j is interference node then

20) 标记j为干扰节点;

21) else if node j is passive node then

22) 标记j为被动节点;

23) else

24) 标记j为主动节点;

25) end if

26)end for

27)如果节点信息列表仍含有主动节点，跳到第3)步;

28)将具有相同标签的节点划分到一个社区当中，算法结束

3．2 时间复杂度

与LPA相比，FNCS_LPA的总体时间复杂度没有改变。首先按照节点中心性度量值对网络节点进行排序，排序算法选择较快的桶排序，其时间复杂度接近于O(n)，n表示网络中的节点个数。初始化节点信息列表的时间复杂度是O(n);从节点信息列表中随机选择一个节点时间复杂度为O(1);更新当前节点的标签的时间复杂度是O(di)，di是节点i的度数，因此在整个更新过程中，时间复杂度是O(m)，m是边的个数。通过使用节点信息列表，算法的收敛比较简单，仅仅判断节点的状态标记即可，最差的情况是 O(n)。因此FNCS_LPA算法的总体时间复杂度是O(m)。

4 实验结果与分析

为了验证FNCS_LPA的有效性，本次实验选取了第1章提到的 NIBLPA［5］、Cen_LP［6］和 NILPA［7］三种较好的改进LPA，数据集选取了表1和表3中的8种真实网络数据集和表6中的4种LFR基准网络数据集。其中式(6)的c1的值为1，c2的值为0．2，式(8) 的 Radio值为0．4。

4．1 执行速度对比

将FNCS_LPA、Cen_LP、NIBLPA和NILPA分别应用到真实网络数据集中进行社区发现。为了具有可比性，每一个算法的终止条件都是节点标签成为邻接节点中的最大值标签，对每一个网络重复100次实验求平均的迭代次数，得到的结果如图3所示。

图3 FNCS_LPA与三种改进LPA的迭代次数对比Fig．3 Comparison of iterations between FNCS_LPA and other three improved LPA algorithms

从图3可以看出，与Cen_LP相比，FNCS_LPA在所有的数据集上的迭代次数明显要比Cen_LP少很多，这是因为FNCS_LPA避免了很多不必要的更新。在 karate、dolphins、polbooks和netscience网络上，FNCS_LPA的迭代次数是Cen_LP的1/4至1/2左右;在Email、CA-GrQc和PGP网络中，算法的迭代次数是Cen_LP的1/10左右;而在CA-Hepth数据集上，算法的迭代次数是Cen_LP的1/30左右。与NIBLPA相比，FNCS_LPA在各个数据集上的迭代次数为NIBLPA的1/16到1/3左右。与NILPA相比，FNCS_LPA在各个数据集上的迭代次数为NIBLPA的1/14到1/2左右。综上所述，与其他三种算法相比，FNCS_LPA明显提高了算法的执行速度。

4．2 模块度对比

将4种算法应用在8种真实网络数据集上进行社区发现，并在最低模块度、平均模块度和最高模块度方面进行对比，模块度的计算公式如式(1)所示。平均模块度(average)是对每一个真实网络作100次实验求取的平均值，最低模块度(min)和最高模块度(max)分别是对每一个真实网络作100次实验后求取的最差结果和最优结果。模块度的对比如表8所示，其中加粗的数据表明4种算法中对应每一个网络的最好结果。

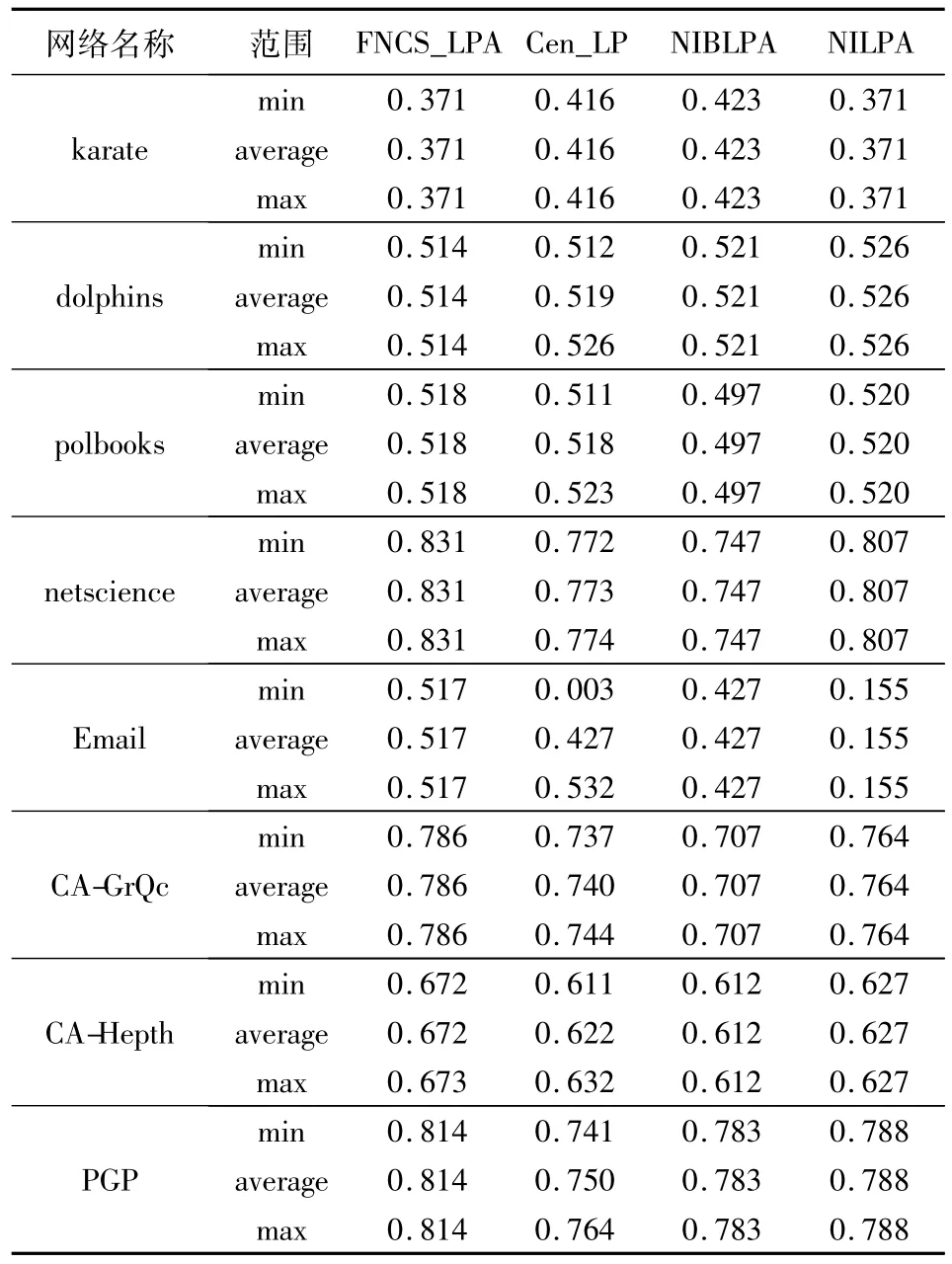
表8 FNCS_LPA与三种改进LPA算法模块度对比Tab．8 Comparison of modularity between FNCS_LPA and other three improved LPA algorithms

从表8中可以看出，FNCS_LPA在所有的数据集上的最低模块度、平均模块度和最高模块度均完全一致。在karate网络上，FNCS_LPA和NILPA都将网络划分为两个社区，求得的结果与真实划分完全相同;在dolphins和polbooks网络上，FNCS_LPA在最低模块度、平均模块度和最高模块度上，均接近于最优解;尽管Email网络没有在最高模块度方面取得最好的结果，但是从平均模块度和最低模块度方面，FNCS_LPA仍是最有优势的;而在netscience、CA-GrQc、CA-Hepth和PGP等网络上，FNCS_LPA的模块度明显高于其他几种算法。综上所述，FNCS_LPA相比其他3种算法提高了社区发现的准确率和稳定性;尤其在较大规模的网络算法，算法的优势更加明显。

4．3 归一化互信息对比

本次实验将4种算法应用在表6中的LFR基准网络数据集上进行社区发现，并在归一化互信息度量(NMI)方面进行对比，NMI的计算公式如式(7)所示。对每一个网络重复100次实验求取平均NMI值。实验结果如图4所示。

图4 LFR基准网络上FNCS_LPA与三种改进LPA算法的NMI对比Fig．4 NMI comparison of FNCS_LPA and other three improved LPA algorithms on LFR benchmark network

从图4可以直观地看出，随着mu的值不断增大，社区结构越来越不清晰，4种算法的社区发现准确率都在下降。从图4(a)可以看出:当mu的值在0．1～0．4时，4种算法都能较好地发现社区结构;mu的值在0．4～0．8时，FNCS_LPA的NMI的值高于其他3种算法。在图4(b)中，mu的值在0．35～0．45时，FNCS_LPA 略低于 NILPA;但 mu 的值在 0．6～0．8时，FNCS_LPA的 NMI值都是4种算法中最高的。图4(c)和图4(d)产生了类似的效果，当mu的值大于0．5时，FNCS_LPA社区发现的准确率明显高于其他3种算法。综上所述，FNCS_LPA相比其他3种算法提高了社区发现的准确率;尤其对于社区结构不清晰的网络，FNCS_LPA的效果更好，准确率更高。

5 结语

本文提出了基于节点中心性和社区相似性的快速标签传播算法。首先，该算法计算每一个节点的中心度量值，依据节点中心性度量值升序将节点加入节点信息列表，利用节点信息列表指导更新过程，通过记录每一个节点的更新状态，避免了许多不必要的更新，减少了迭代次数，从而提高了社区发现的稳定性和执行速度。为了验证基于节点中心性的快速更新过程的有效性，实验使用了8种真实网络在迭代次数和平均模块度方面与LPA进行了对比。其次，算法引入社区相似性的更新规则，即当前节点会加入与当前节点社区相似性最高的社区，提高了社区发现的准确率，为了验证基于社区相似性的更新规则的有效性，算法在平均模块度、NMI方面与LPA进行了对比。最后，将基于节点中心性的快速更新过程和基于社区相似性的更新规则结合形成本文提出的基于节点中心性和社区相似性的快速标签传播算法，与目前3种改进的LPA在迭代次数、模块度和NMI三个方面进行了对比，实验结果表明FNCS_LPA在提升算法执行速度的基础上，提高了算法的稳定性和准确率。