一种连续多脉冲相参海杂波的仿真方法
屈高龙,王文光,翟宇霄
(北京航空航天大学,北京 100191)
0 引 言
随着相参雷达的应用日益广泛,有关相参积累实现目标检测的研究越来越多,传统的脉冲多普勒雷达信号处理中,由于积累的脉冲数较少,脉冲积累的时间通常比较短,积累效率较高。现代雷达面临的工作环境日益复杂,为了检测“低可观测目标”,常采用长时间积累技术,其积累时间达秒级甚至更长[1]。经典的处理如基于FFT的MTD(Moving Target Detection),积累增益依赖于积累的脉冲数目,但随着雷达分辨率的提高,当目标高速运动时,在一个较长的相参积累时间间隔内会出现距离走动和多普勒扩展的情况,基于此,基于Keystone的距离补偿[2]以及RFT[3](Randon-Fourier Transform)、RFRFT[4](Randon-Fractional Fourier Transform)等方法应运而生,通过不同的方法进行距离和多普勒补偿,从而获得较长的积累时间。
研究表明,在高分辨率雷达对海观测时,低擦递角或者高海况情况下,海浪失去平衡状态,出现浪花,从而产生了破碎波,破碎波的雷达后向散射会表现为海尖峰[5],这时,雷达回波强度会明显增强,表现为随机分布在不同距离、不同角度上的零星的运动或者静止目标,使海杂波的概率密度曲线表现出较长的“拖尾”现象,通常海尖峰的持续时间较短,且持续时间内具有较强的相关性。在目标探测中可能会将海尖峰判断为目标,导致虚警率的增加[6]。
由于海杂波散射机理的复杂性和影响因素的多样性,目前还没有能够描述各种海况的统一的海杂波仿真模型,代表性的模型主要包括Lee模型,Walker模型和Ward模型(混合高斯模型)[7-9],Lee模型将海杂波多普勒功率谱表示为几个谱分量,分别是与Bragg散射有关的Gaussian谱分量,与Burst散射有关的Lorenztian谱分量,以及与Whitecap散射分量有关的Voigatian谱分量。后来,Walker将Lee模型进行近似和简化,采用三个分量的组合高斯模型描述海杂波的多普勒谱,这三个分量分别为Bragg分量、白浪以及海尖峰分量,其中海尖峰多在HH极化时出现[7]。Ward模型假定多普勒谱形状采用类似于K分布的尺度高斯混合模型,将海杂波的多普勒谱看成被随机功率常数调制的混合高斯函数。Watts通过对实测数据的单个谱的多普勒频移和谱宽分析,建立了平均多普勒频移与强度之间的线性经验模型,然后分别在多普勒域和时间域进行相干杂波仿真,产生了连续多普勒谱和具有一定相关性的相干时间序列数据[10-11]。Michael McDonald等[12-14]人从快变的散斑分量和慢变的纹理分量入手,利用时空相关特性对海杂波进行建模,并用实测数据验证了模型的准确性。
近年来已有很多模型用于海杂波特性描述和建模仿真,如K分布模型[9],复合高斯模型[15-17]等等。但是这些模型方法主要从幅度统计特性和功率谱特性上描述海杂波,这不能满足海杂波背景下相参积累研究对数据相位的需求,完全随机产生的海尖峰也与实际场景不符。
针对现有海尖峰仿真模型和方法的不足,本文给出了一种能够反映海尖峰特性、脉间相关性以及海杂波频谱特性的连续多脉冲相参海杂波的仿真方法,该方法将为深入开展海杂波背景下的目标检测,尤其是为海面弱目标的长时间相参积累算法研究提供仿真数据。
1 海杂波的经验模型
GIT模型[18]可以很好地描述实测海杂波的反射系数,K分布是目前最接近描述实测数据概率密度分布的一种模型[19]。而针对多普勒谱的分析也有Walker和Watts等人得到的经验模型。本节针对海杂波的三个主要特性:后向散射,幅度统计特性和多普勒谱进行介绍。
1.1 后向散射模型
GIT模型是一种σ0的海杂波经验模型。该模型在雷达频率1~100 GHz,擦地角0.1°~10°的范围内是有效的。
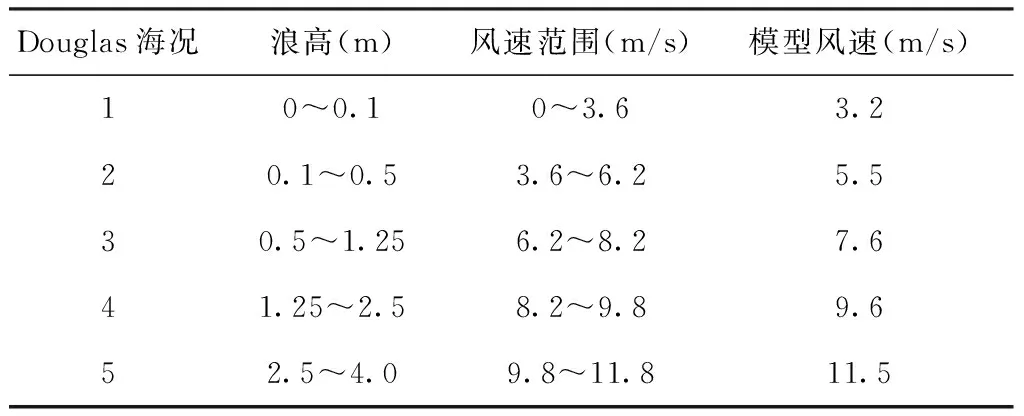
表1 Douglas海况情况
GIT模型的计算与海况是密切相关的,在雷达性能指标中,关于海况的定义经常是有歧义的,表1给出了Douglas海况参数,它是Nathanson[20]在反射系数表中使用的一种海况等级。GIT模型有三个分量组成,海况分量Aw、多径分量Ai和风向分量Au,且每个分量都包含多个参数。对完全发展的海表面,风速U和海况有一个简单的关系式[8]:
U=3.16s0.8
(1)
其中SS为Douglas海况。已知平均浪高hav和风速的关系为:
hav=0.004 52U2.5
(2)
海表面粗糙度参数定义为:
(3)
其中λ为雷达工作波长;φgr为雷达擦地角,粗糙度σφ可用于估计多径分量:
(4)
风的影响与风向有关,并且依赖于雷达擦地角,随着擦地角φgr的减小而增加,引入风向相关性:
Au=exp(0.2cos(θw)(1-2.8φgr)(λ+0.015)-0.4)
(5)
其中,θw为风向与雷达观察方向的夹角。
海况的变化包含于最后一个因数中:
(6)
则不同极化方式下的GIT模型为:
1.27ln(φgr+0.0001)+9.7
(7)
1.2 海杂波幅度分布模型
海杂波的幅度分布模型有很多,所有这些模型均是通过函数形式表示观测的分布特性,K分布模型是高分辨率雷达海杂波建模中常用的模型之一,除了可以在很宽的范围内有效拟合实际海杂波,而且还可以比较准确的描述海杂波的脉间相关特性。
K分布的复合形式被分解为具有不同去相关时间的两个杂波分量,一个是慢变的纹理分量,通常用取平方根的伽马分布来表示,具有秒级的去相关时间,并且该相关性和风速等自然环境有很大关系,一般不受频率捷变的影响;第二个是快变的散斑分量,它是由各个散射单元中杂波的多路径散射产生的,具有毫秒级的去相关时间,可以通过散射体频率捷变去相关。K分布的概率密度函数定义为[21]:
(8)
其中,Kv(·)为v阶修正第二类Bessel函数;Γ(·)为伽马函数;v为形状参数,描述K分布的倾斜度。v的取值范围通常为0.1 Walker模型把海杂波的多普勒功率谱表示成两个或三个具有不同均值和方差的高斯分量的线性叠加,这些分量的均值和标准差分别对应于Bragg散射、Burst散射、Whitecap散射的多普勒频移和多普勒带宽。 对于HH极化,该模型为: (9) 对于VV极化: (10) 本文主要在SIRP(Spherically Invariant Random Process)方法K分布海杂波仿真的基础上,进一步从海尖峰重排、脉间相关处理和谱型滤波三个方面对连续多脉冲相参海杂波仿真,下面分别对海尖峰重排,脉间相关处理和多普勒谱型滤波等方面进行说明。 本文所给出的连续多脉冲相参海杂波的仿真研究框图如图1所示。 图1 连续多脉冲相参海杂波的仿真研究框图 基于SIRP方法产生的K分布海杂波中包含了海尖峰,但是海尖峰在每个脉冲回波中的位置是完全随机分布的,实际场景中的海尖峰具有一定的存活时间,而且完全随机的海尖峰不能反映出长时间积累中海尖峰对目标检测造成的影响。基于此,本文给出了一种海尖峰重排的方法:首先从海杂波背景中选择部分强点作为海尖峰,根据设定的存活时间设定第一个脉冲回波中的海尖峰存活时间,依次对后续脉冲回波中的海尖峰进行位置重排,保证存活期间海尖峰位置稳定。假定第i个脉冲回波中含有M个海尖峰。第i+1个脉冲回波检测到海尖峰N个。当N≥M时,需要对第i+1个脉冲回波中的M个海尖峰位置重排,另外N-M个海尖峰为新生海尖峰。当N 根据Walker模型[8],海杂波数据的多普勒谱符合高斯分布,由维纳-辛钦定理,对于具有高斯型功率谱的海杂波,做逆傅里叶变换得到自相关函数: (11) 式中,σv为海浪运动速度的均方根值,可以根据GIT模型计算得到。 按照分布模型产生的不同脉冲的回波数据相互独立,为使第i个和第i+1个脉冲的回波具有一定的相关性,采用相邻两脉冲数据加权叠加的方法,其中的加权系数决定了两帧数据的相关性。对于仿真的海杂波数据,可以利用式(11)得到两帧数据的相关系数,然后利用式(12)得到具有一定脉间相关性的第i+1个脉冲对应的海杂波: (12) 式中,ci和ci+1分别为第i个和第i+1个脉冲的回波。 Walker等人验证了海杂波数据的多普勒谱符合高斯分布,由于利用复合高斯模型产生的仿真数据,在进行相参积累研究中,同一距离门上的多个脉冲回波无法反映出海杂波本身的多普勒特性,为了保持高斯分布约束,还需要对海尖峰重排后的数据按照距离门进行滤波,使得每个距离门的数据具有给定的谱型。 仿真采用Walker模型,将海杂波的多普勒谱分解为三种高斯型谱的线性叠加。三种高斯型谱的频谱峰值和谱宽采用J.L. Whitrow[21]给出的计算方法,以Bragg成分为例,其谱峰位置和谱宽计算如下: (13) WB=(4.6+0.68Ucosφ)0.021/λ (14) (15) GIT模型与Walker多普勒模型结合,得到: (16) 对于各个高斯分量的系数,文献[21]给出了计算方法。 (17) (18) 最后,根据求得的各个高斯分量系数,并利用式(9)或式(10)进行多普勒谱滤波。 为了验证所给出的海杂波仿真模型的有效性,利用实测数据分别从幅度统计特性、相关性以及多普勒谱特性等方面对本文给出的仿真方法进行比较分析。 本文所用实测数据来自CSIR Fynmeet雷达,其中数据CFC17-010是2006年8月3号在南非的西南海岸线采集所得,该雷达只有垂直极化方式, 其详细参数如表2所示[22]。 表2 实测数据参数说明 实测数据CFC17-010是在风速13.3 m/s,海浪平均高度2.38 m的海洋环境下测得的。 仿真实验中,根据表2设置雷达回波持续时间59.9488 s,脉冲重复频率为5 kHz,波长0.03 m;根据实测数据的海洋环境,设置GIT模型海况为6、风向与雷达观测方向夹角为π、擦递角为0.472deg,计算得到平均浪高约为2.88 m,风速约为13.24 m/s,这与实测环境近似;设置海尖峰至少存活0.06 s,空间宽度跨越2个距离门。根据第三节给出的方法,得到SIRP仿真数据与本文仿真海杂波数据的距离-时间强度如图2所示。 图2 SIRP仿真数据与仿真海杂波数据距离-时间强度图 图2(a)为SIRP方法产生的仿真数据距离-时间强度图,图2(b)是本文给出的方法得到的海杂波数据的距离-时间强度图。 从图2(a)可知,根据K分布模型产生的海杂波数据在每个距离门内的峰值位置是随机的,这不能满足海尖峰存活时间的要求。采用本文给出的流程,对SIRP仿真数据进行海尖峰重排、脉间相关、谱型滤波处理。首先用K分布分别拟合仿真海杂波数据与实测海杂波数据,得到图3所示的拟合效果。 图3 仿真海杂波数据与实测数据幅度统计特性对比 图3(a)为本文方法得到仿真海杂波数据的幅度统计K分布拟合效果,图3(b)为实测海杂波数据K分布拟合效果,可以看出仿真数据和实测数据都可以很好地拟合于复合K分布,且由于海尖峰重排,仿真数据与实测数据均存在尾部偏离现象。 为验证仿真模型的连续脉间相关性,对仿真海杂波数据和实测海杂波数据分别计算相邻脉冲间的相关系数并做归一化处理,结果如图4所示。 图4 仿真海杂波数据与实测海杂波数据相关特性对比 图4(a)为仿真海杂波数据的脉间相关特性,图4(b)为实测海杂波数据的相关特性,通过比较,可以看出本文方法可以得到具有一定脉间相关的海杂波数据,且与与实测数据的脉间相关系数范围一致。 根据Walker给出的三个高斯分量的叠加模型,对仿真海杂波数据在多普勒谱上进行谱型滤波处理。以第一个距离门的数据为例,采用64点FFT计算多普勒谱。结果如图5所示。 图5 仿真海杂波数据与实测海杂波数据多普勒谱特性对比 图5(a)为仿真海杂波数据的多普勒谱,图5(b)为实测海杂波数据的多普勒谱。可以看出,在近似的环境下,两者均具有较窄的谱宽、较明显的多普勒频移,且谱宽和峰值位置范围具有一致性。 本文针对基于幅度统计特性的海杂波仿真方法不能满足相参积累的要求的现状,给出了一种包括海尖峰仿真、脉间相关处理和谱型滤波等过程的连续多脉冲相参海杂波的仿真方法。现有的基于SIRP的K分布海杂波仿真中,海尖峰是完全随机分布的,本文基于此,给出了海尖峰重排、脉间相关和距离门多普勒滤波处理的具体方法,实现了对连续多脉冲海杂波的仿真。利用实测的CSIR数据与仿真模型得到的海杂波数据的对比试验表明,本文给出的仿真方法能够较好的仿真海尖峰的时间持续性,具有与实测数据类似的脉间相关性和脉间多普勒特性。实验表明,本文所给出的是一种有效的连续多脉冲相参海杂波的仿真方法,将为海上弱目标的长时间相参积累提供有效的仿真数据。1.3 海杂波多普勒谱模型
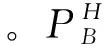
2 连续多脉冲相参海杂波仿真方法

2.1 海尖峰重排
2.2 脉间相关处理
2.3 谱型滤波
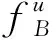

3 仿真实验分析

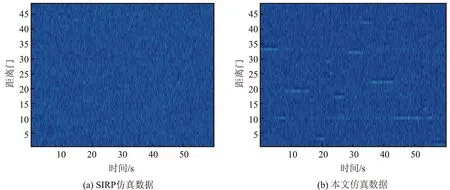
3.1 幅度统计特性

3.2 连续脉间相关性
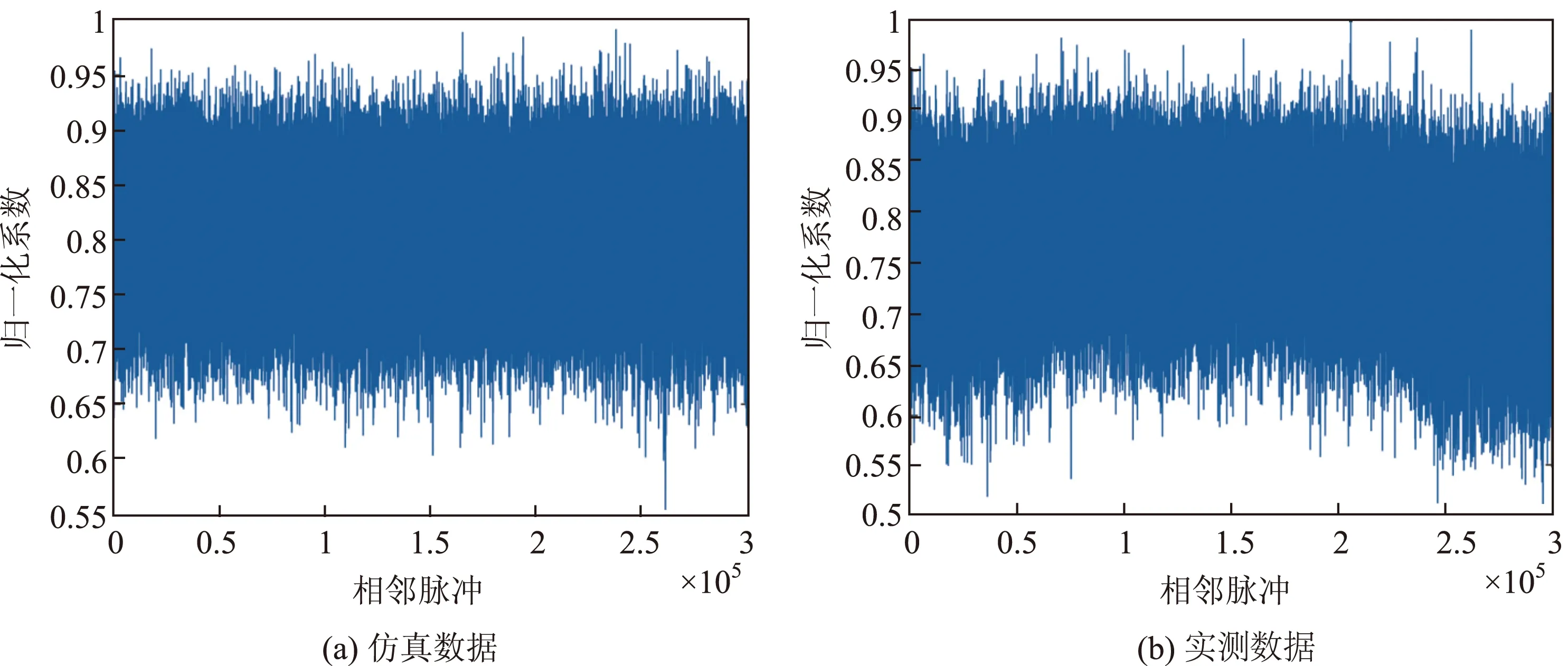
3.3 多普勒谱特性
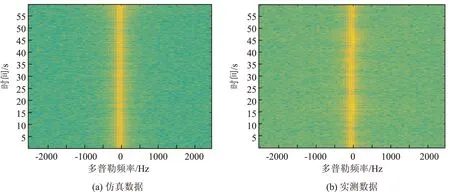
4 结 语

