基于对标学习的智能优化算法

谢安世



基于对标学习的智能优化算法

谢安世

（浙江工业大学，浙江 杭州 310014）

科研、工程和管理中的很多问题都可以转化为优化问题。应用于这些优化问题的各种方法本身就是各种模型，设计不同的方法即设计不同的模型。将标杆管理理念建模成为一种用于单目标优化问题的元启发式搜索方法。基于奥卡姆剃刀原则，摒弃了复杂的操作算子的概率调优规则，用一个简单的框架来组织核心算子，从而达到许多组合算法的搜索效果。

智能优化算法；探索性与开发性；全局搜索与局部优化；标杆管理

1 引言

元启发式优化/搜索算法的研究，从横向看，可以分为算法自身设计研究（即设计不同的优化搜索算法）、算法自身的理论研究（包括复杂度、收敛性等）和算法在各学科领域的具体应用研究共3个方面。单从算法自身的设计看，大体可以分为两个层次：一是对已有的算法进行改进，主要体现在改良现有的（或设计出新的）操作算子及其概率规则；二是提出全新的算法。

目前很多新提出的算法，基本上都由几个广泛使用的核心算子组成，它们的“新”，只是用一种别的“新”物种来命名常见的元启发式搜索[1]。事实上有很多高被引算法都是一些经典算法的翻版，只是名称不同[2]。因为自然界现象的多样性，最近十几年来有越来越多各种各样的所谓新算法不断地被提出，都喜欢使用各种隐喻，看起来好像挺热闹，但如果就科学的求真求实来讲，真的有必要吗[3]？同时由于各类隐喻的特殊性，在用于算法设计时，只有某种特定的编码方案才能很好地实现这种隐喻。换一种编码方案，就不容易实现这种隐喻了，即算法的“智能性”也就大打折扣了。比如粒子群算法，由于其特定的候选解更新方案，用浮点数编码，效果很好，用二进制编码、字符串编码或者布尔型编码，效果就不好。因此，这类算法的搜索效果很大程度上依赖于其核心操作算子的概率规则，在运行过程中需要参数调优才能平衡其搜索过程的探索性（exploration）与开发性（exploitation），并借此保持搜索过程中的种群多样性。

本文也使用了隐喻手法，借用企业管理领域中的标杆管理理念，将“见贤思齐”这一思想建模为一种通用的优化/搜索框架。不限于某种特定的编码方案，并且不需要特定的概率规则，只需将核心操作算子按本文给出的组织策略进行组织安排，算法就可以平衡其搜索过程的探索性与开发性，并保持搜索过程中的种群多样性。因此说本文提出的算法的“智能性”，没有体现在操作算子的概率规则上，而是体现在操作算子的组织策略上。

2 对标学习算法的基本框架

对标管理，顾名思义，就是以知己知彼的方式，检验自己并了解对手，从而知道自己与竞争对手的差距，以便学习和改进。基于对标管理思想的优化算法，其总体思路如下。

在整个生态系统（即解空间）内，通过某种规则产生若干小生境种群（即初始解集），相当于全球市场上各类企业主体，种群内的个体相当于企业部门或员工。首先根据优化目的，以评价函数为衡量标准，进行立标管理，分别确定各小生境种群内的最佳个体（即局部最佳个体、局部最优解）和整个生态系统内的最佳个体（即全局最佳个体、全局最优解），相当于树立企业内部标杆和企业外部标杆，并记录在案。种群内的个体，按照对标学习的指导原则进行对标学习。这一轮立标管理与对标学习完成之后，再次进行评估，重新树立标杆，并更新记录。然后开始新一轮的对标学习，如此往复，直至满足迭代停止条件。此时的全局最佳个体，解码之后便是全局最优解，各局部最佳个体，解码之后便是局部最优解。由此可知，这是一种同时包含学习性竞争与竞争性学习的寻优思想。

2.1 对标学习算法的简单版本

简单对标学习算法，主要是指全局标杆由全程最优个体担任；局部标杆由当代最优个体担任；试探性学习策略分别嵌套在全局对标学习和局部对标学习两个操作算子之内；全局对标学习、局部对标学习和自我学习3个基本操作算子的概率都取随机数。基本步骤如下。

步骤1 初始化种群和个体的数目，迭代停止条件等。

步骤2 根据对标管理的指导原则，评估所有个体的适应度值，记录并更新标杆。

步骤3 根据对标学习的具体方法，个体有选择地执行对标学习。

步骤4 若迭代停止条件不满足，转向步骤2，否则输出标杆并解码。

2.2 对标学习的指导原则

基于对标管理思想的优化理论，其总体思想是对标学习，但其核心思想与根本精髓，则是对标学习的指导规则和对标学习的具体方法。对标管理的规则是中观的，是针对具体问题设计具体算法，其内容如下。

（1）立标记录实时更新。在算法运行过程中，每一轮产生的标杆，包括局部标杆与全局标杆，均记录在案，并不断更新。

（2）对标学习按需选择。个体在进行对标学习时，3个操作算法无需按顺序执行。某个体如果执行全局对标学习之后没有获得改善，则继续进行局部对标学习，否则直接退出本轮对标学习。

（3）学习对象灵活切换。随着算法运行，理论上每次迭代之后的局部（和全局）标杆将不断变化。但为了避免极端状况，可以设定规则强制要求各个小生境种群相互交换局部标杆，从而保证生态系统内的全局极值点能被搜索到。

（4）高效利用马太效应。个体在执行对标学习时的欲望和强度，也即操作算子的概率，可以根据个体自身与标杆对象的差异度和相似度来决定。基于标杆管理的优化思想规定，这个差异度越小，或相似度越大，则其学习欲望就越大，随之其学习强度也越大，这是个体层面的马太效应。

（5）合理利用集群效应。在对标学习过程中，如果某个种群发现了更好的全局解，则其他种群将指派部分个体进入该种群，以协助进行密集搜索。但如果某种群在对标学习过程中一直都没有发现更好的全局解，则种群内所有个体将逐渐被调配往其他种群，这是种群层面的集群效应。

2.3 对标学习的具体方法

对标学习的总体原则就是见贤思齐。具体来讲，就是个体减少其自身与标杆对象之间的差异度，并（或）增加其自身与标杆对象之间的相似度。具体怎样实现这种对标式学习，取决于算法本身采用的编码方案。下面给出几种常见的编码方案及其相应的对标学习方法。

2.3.1 0/1编码方案下的对标学习方法

常见的0/1编码方案，有二进制码（binary）、格雷码（Gray-code）以及独热码（one-hot）。这3种编码方案，针对不同的问题，各有优势，也各有缺点。对于这三者的联系和区别，这里无需详述，只是对于智能优化算法来说，采用二进制码时，个体（即候选解）的编码与解码过程，相对比较简单，消耗的计算时间较少，但对于个体之间的转码操作，即对于候选解的搜索操作，相对复杂，消耗的存储空间较多。采用格雷码或独热码时，编码与解码操作相对复杂，消耗的计算时间较多，但是转码操作相对简单，消耗的存储空间较少。此种情形，与数字控制系统中的情形，刚好不同，二进制编码与格雷码编码，使用触发器较少，对组合逻辑消耗较多，而独热码编码则相反。

当算法采用0/1编码方案时，使用海明距离度量个体之间的差异度。个体对标学习的具体方法，就是减少自身与标杆对象之间的海明距离。搜索方向和搜索步长的调整，主要体现在对自身坐标基因的调整上。个体对标学习欲望的强弱，主要体现在学习率的大小上。个体对标学习行为的强度，主要体现在编码基因位调整的个数上。

2.3.2 浮点数编码方案下的对标学习方法

当采用浮点数编码方案时，一般可以使用距离概念来表征个体之间的差异度，用相关系数来表征个体之间的相似度。对于表征差异度的距离概念，可以采用闵可夫斯基距离（Minkowski distance），根据问题特征和数据结构，选取合适的参数值，容易简化成曼哈顿距离（Manhattan distance）、欧几里得距离（Euclidean distance）、切比雪夫距离（Chebyshev distance）等。对于表征相似度的相关系数，也可以根据问题需要和数据特征，选取合适的计算方法，如皮尔逊相关系数（Pearson correlation coefficient）、夹角余弦相似度（cosine similarity）、Tonimoto系数、Spearman相关系数、Kendall相关系数等。

当算法采用浮点数编码方案时，个体对标学习的具体方法，就是减少自身与标杆对象之间的闵可夫斯基距离，并（或）增大自身与标杆对象之间的相关系数。

另外，针对浮点数编码，必须特别注意以下两个问题。一是关于合理选用度量差异度与相似度的方法问题。个体之间的差异度与相似度，从字面意义来看，只是两个相对应的概念，似乎从算术上可以相互转换。但是站在计算机科学与数据科学的角度来看，这是两个完全不同的概念，有着不同的确切定义，其内涵和外延是完全不同的，不能相互转换。这里用距离概念衡量的差异度，与用相关系数衡量的相似度，在不同的分析模型与数据结构之下，两者的差别非常大。差异度，更多的是体现编码数值上的大小差别，而相似度，更多的是体现编码方向上的区别。在计算和搜索过程中，可能会出现这样一种现象，即个体之间的差异度发生改变了，而相似度却没有变化，或者相反，个体之间的相似度发生改变了，而差异度却没有变化。因此，在针对具体的优化问题设计具体的优化算法时，需要根据其分析模型与数据结构，选用合适的度量方法。二是算法设计与测试中浮点数的转码、计算与精度问题。符合IEEE754标准，支持SSE2指令集的绝大多数CPU/GPU，是当前进行算法设计与测试的硬件基础。但是按照IEEE754标准规定的浮点存储格式，有一些带小数位的十进制数据，无法使用当前计算机所使用的0/1二进制代码准确表示出来。因此在转码与计算时，如果没有合理的处理方法，会出现精度失准的问题。浮点数及其转码与计算的精度，很大程度上取决于指数范围的大小。以现行的32位单精度浮点数为例，最低不能低过2-7-1，最高不能高过28-1（其中剔除了指数部分全0和全1的特殊情况）。如果超出表达范围，那就得舍弃末尾的小数，造成向上或向下溢出，甚至有时候舍弃都无法表示。这样在需要表达一个极小的数值时，如果不用规格化数值表示，CPU就只能把它当0来处理。如果多次做低精度浮点数舍弃，则必然精度失准严重，甚至会出现除数为0的情形，从而导致计算异常。如果做非规格化浮点处理，虽然可以补救精度失准的问题，但对于CPU硬件或编译器要求甚高，转码和计算的效率将呈指数下降。因此智能优化算法在设计和测试时，不仅要考虑问题域特征，还要考虑计算过程中的硬件CPU/GPU、软件编译器问题。最后返回计算结果时，还有算法自身的解码环节，即二进制机器码与浮点数之间的转码，这涉及算法代码优化问题，不再赘述。

2.3.3 字符（串）编码或布尔值编码下的对标学习方法

现代管理工作中，尤其数据管理工作中的许多问题，比如电子商务领域常见的商品评价与推荐问题，涉及人机交互，许多模型必须使用符号函数，往往需要字符或字符串编码，或者布尔值编码。

当采用字符（串）编码或布尔值编码方案时，一般可以使用Levenshtein distance（编辑距离）、Jaro-Winkler distance（哈罗-温克勒距离）、Jaccard coefficient（杰卡德系数）等概念来表征个体之间的差异度或相似度。个体对标学习的具体方法，就是通过基因编辑，减少自身与标杆对象之间的距离，并（或）增大自身与标杆对象之间的相似度。

3 对标学习算法的若干技术

3.1 智能性

基于概率搜索的智能优化算法，其智能性主要体现在概率规则的制定上。这个概率规则，主要是指算法在运行过程中，其设计的操作算子被执行时的概率规则。因此，几乎所有的智能优化算法，除了需要为操作算子的概率设置初始值之外，还需要为其设计一套相应的变化规则。比如遗传算法及其各种改进版本，需要为选择、交叉和变异这3个操作算子的概率设置相应的初始值和变化规则；粒子群算法及其各种改进版本，需要为其惯性权重和加速系数设置合适的初始值和变化规则；蚁群算法及其各种改进版本，需要为其信息素和启发式因子设置合适的初始值和变化规则。这些概率的初始值及其变化规则，设置恰当与否，决定了算法能否搜索到问题的最优解，甚至直接决定了算法能否正常发挥其应有的搜索性能。但是，概率参数如何配置，才能使得算法的优化性能达到最优，这本身就是一个组合优化问题。目前该问题在理论上尚没有得到很好的解决，因此，几乎所有智能优化算法，在概率参数的配置上，主要依靠统计经验。这也是目前所有智能优化算法存在着的一个软肋。

本文提出的对标学习算法，完全不存在这个问题。由前文内容可知，对标学习算法，完全不需要为其操作算子的概率设置初始值和变化规则。无论全局学习率、局部学习率，还是自我学习率，在对标学习算法的简单版本中，都是完全随机的。在设计其他版本时，可以为每个操作算子的概率设置相应的初始值及变化规则。但这样一来，不仅增加了算法的复杂性，而且实验表明，这种做法并没有让算法性能有质的提升。实际上，标杆学习算法的搜索性能，不依赖于操作算子的概率规则，而是依赖于对标管理思想，依赖于对标学习的指导原则和具体方法。算法中的基本操作算子，只是对标学习思想及其指导原则在特定的编码方案和特定的数据结构之下的一种具体实现而已。事实上，只要遵循对标管理的若干思想和若干原则，设计出特定的编码方案及相应的数据结构之下的学习方法，自然就会获得优良的搜索和优化性能。这种无需概率规则的制度设计，完全避免了概率规则对于算法性能的影响。对标学习算法的“智能性”，完全没有体现在操作算子的概率规则上，而体现在了操作算子的组织策略上。

3.2 探索性与开发性的自动平衡

探索性体现了算法进行全局搜索，开拓新空间的能力，而开发性体现了算法进行局部优化，小幅改善求精的能力。一般来说，一个算法的探索性越强，则其开发性就越弱，反之亦然。因此传统上，算法的探索性与开发性是一对矛盾体，相互冲突和对立，无法相容。如果探索性太强而开发性太弱，则搜索结果容易发散，容易错过全局最优解，最终不利于对全局极值的搜索；如果探索性太弱而开发性太强，则搜索结果容易集聚，容易陷入局部最优解，最终也不利于对全局极值的搜索。判断一个智能优化算法的性能如何，其中最为重要的一点，就是看其采用什么策略来平衡其全局搜索与局部优化。算法的探索性与开发性权衡的策略，在很大程度上决定了一个算法的优劣。为了平衡算法的探索性与开发性，目前现存的智能优化算法采用的策略，几乎都是给不同的操作算子附加相应的概率参数。在这个概率参数的取值上，具体做法大体有两种，一是根据统计经验提前设定某个（些）固定值，二是根据某些原则在搜索过程中自适应地动态调整。比如遗传算法及其各类改良版本，往往都是通过选择率、交叉率和变异率3个参数来平衡其探索性与开发性；粒子群优化算法及其各类改良版本，往往都是通过一个惯性权重和两个加速系数来平衡其探索性与开发性；蚁群优化算法及其各类改良版本，往往都是通过信息素浓度这个参数来平衡其探索性与开发性。在这个概率参数的取值上，每个算法虽然各有自己的技巧，但都不尽如人意。因为这个概率参数，作为控制变量，其取值问题本身也是一个待解的优化问题，尚未得到圆满解决。事实上，无论使用什么技巧来设定这个概率参数，其取值及相应的平衡效果可能都不是最优的。因此，总体而言，现存的智能优化算法，对于全局搜索与局部优化，即探索性与开发性，如何平衡的难题，没有得到很好的解决。

人们认为算法的探索性与开发性，其本身是相互对立和无法相容的，但是在算法的设计中，是可以实现协同并存和自动均衡的。因此在算法的设计与开发过程中，探索性与开发性相互对立、无法相容的“潜规则”是完全可以避免的。本文提出的算法框架，抛弃了传统的利用概率参数来平衡算法探索性与开发性的策略。事实上，只要是根据对标学习的指导原则，即不依赖控制参数，而是依靠科学合理的制度，设计出来的优化算法，其全局搜索与局部优化，即算法的探索性与开发性将会协同并存，并且会自动平衡。在本文提出的通用框架之内，个体进行全局对标学习，就相当于对未知极值点的概率分布进行探索，这样进行全局搜索，就起到了开拓新空间的作用，体现了算法的探索性。个体进行局部对标学习，就相当于根据当前的观测值，利用已知的动作获取更多回馈以使下一次“收益最大化”，这样进行局部优化，就起到了小幅改善求精的作用，体现了算法的开发性。对标学习的指导原则中第二条，即学习行为按需选择的设计原则，使全局对标学习行为与局部对标学习行为，在同一轮的迭代搜索中，都得到执行。这样同轮异步的制度设计，巧妙地解决了全局搜索与局部优化无法并行共存的难题，从根本上保证了算法探索性与开发性的自动平衡。这个特点，在后面的仿真实验中也得到了证实。

3.3 对于探索性与开发性自动平衡的实验证明

现以MATLAB内置的Peaks函数为例，测试本文提出的对标学习算法如何实现探索性与开发性的自动平衡。本次测试使用对标学习算法简单版本，初始阶段生态系统内共有5个小生境种群，每个种群包含3个个体，即总共包含15个个体。算法采用二进制编码方案，个体的编码长度为30，算法的最大迭代次数设定为100。

这里分两种情形，一是初始种群在搜索空间内随机分布时；二是初始种群被置于搜索空间内同一点（3，3）时。下面分别列出以上两种情况下，生态系统内每一个个体的搜索过程。因为同时在动画中展示15个个体的搜索过程会显得非常混乱，因此每一个个体的搜索过程均使用一张动态图片单独展示，这样就有30张动态图片，显示了个体是如何在探索性与开发性之间实现动态平衡的。从15个个体分别在两种初始分布条件下的搜索过程的动态展示中，可以看到如下3个明显的现象。

一是个体进行了多次“爬山”过程。在搜索过程中，可以很明显地看到，当它居于半山腰时，受到局部标杆的吸引，它产生了多次“爬山”过程，并最终爬到了山顶，实现了对全局最大值的搜索。这个“爬山”过程，相当于根据当前的观测值，利用已知的动作获取更多回馈，以使下一次“收益最大化”，起到了小幅改善求精的作用，体现了对标学习算法的开发性。

二是个体的搜索轨迹几乎遍及整个解空间。算法的最大迭代次数设定为100，即个体只演化搜索100个世代，可以看到，在这100次迭代过程中，个体的搜索路径几乎覆盖了整个解空间。理论上，只要迭代次数足够多，个体可以遍历整个搜索空间。这种大范围的遍历性全局搜索能力，体现了个体开拓新空间的能力，体现了对标学习算法的探索性。

三是所有个体均多次搜索到了全局极大值。比如第一号个体在100次迭代过程中，在初始种群随机分布和同一分布两种条件下，分别有15次和17次搜索到了Peaks函数的全局最大值。这是由对标学习算法的搜索策略决定的，对标学习式的搜索策略使得算法具有很高的搜索效率。

需要说明的是，本次实验所使用的数据，是由算法随便运行一次产生的，并无特意挑拣。

4 对标学习算法对于动态优化问题的应用

4.1 动态函数优化问题设计原因

为什么要设计动态函数优化问题？有3个原因，第一是现实世界中的科学、工程和管理问题，大多都可以转化为最优化问题。第二是这些最优化问题大多都可以转化为对相关数学模型的求解问题。比如，现代信息生物学中预测蛋白质稳定结构的问题，可以转化为求解蛋白质结构的最低势能值问题，而后者，又可以转化为对HP格点模型、AB非格点模型等蛋白质结构简化模型的求解问题；现代分子生物学中肿瘤微阵列基因表达数据的分类问题，可以转化为求解最优的肿瘤特征基因提取和分类模型的问题，而后者，可以转化为对表征样本间距离和相似性的目标函数的求解问题；当代大数据科学中复杂网络的结构测定问题，可以转化为求解最优网络结构的问题，而后者，又可以转化为对网络平衡结构模型的求解问题；现代智能工业移动机器人的实时调度问题，可以转化为机器人的移动路径最优化问题，而后者又可以转化为对移动机器人运动学模型的求解问题。第三是这些静态数学模型是其现实世界当中动态模型的特例，是其真实模型的理想状态。如果一个算法能够很好地求解某个问题的动态模型，则对其理想状态下的静态模型的求解，自然不成问题。

关于动态函数的构造，已经有学者提出了许多种方法。本文使用两种简单的通过静态函数优化问题构造动态函数优化问题的方法。一是改变函数的约束条件，使得搜索空间发生变形，比如静态函数中变量的个数及其取值范围，根据特定的规则发生变化，从而构造动态函数优化问题；二是改变个体基因的编码序列，使得个体基因发生变形。比如当采用0/1编码方案时，所有个体的基因表达式，周期性地与某个特定的模板进行异或运算，从而构造动态函数优化问题。

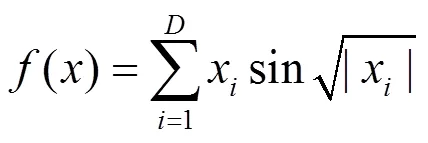
动态问题与静态问题最大的不同，在于其因环境变量不断变化，其最优解不再固定不变，而是随着环境的变化而动态变化。因此对动态问题进行求解，不仅是要求出问题的最优解，更重要的是要跟踪问题最优解的运动轨迹。动态函数优化问题主要用来测试算法对所求解问题的全局极值的动态跟踪能力。

4.2 基于空间变形的动态函数优化

基于空间变形的动态函数优化问题，是这样定义的：Schwefel函数的定义域在±500之间变化时有3个变量；在±1 000之间变化时有2个变量，这样其全局最小值会随之发生漂移。动态函数如下：

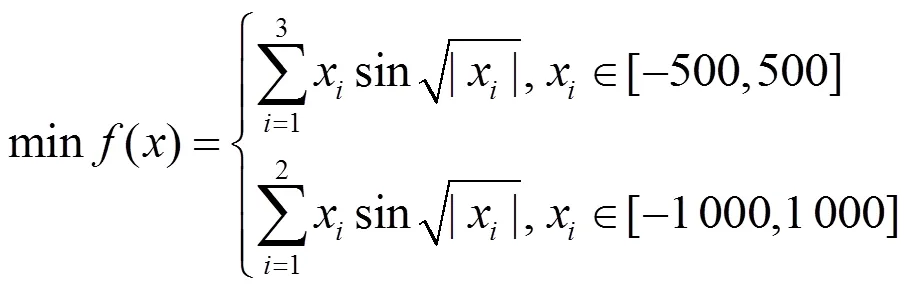
定义域变化大小程度表征环境震荡强度，可以用来测试算法对于函数在不同解空间内全局最小值的动态追踪能力。在本次测试实验中，使用IEEE CEC2017实参数单目标优化竞赛中排名前四的4个算法，分别是jSO[4]、LSHADE-cnEpSin[5]、LSHADE-SPACMA[6]、DES[7]，与本文提出的对简单标学习算法（SBA）进行对比。为保证公平公正，在实验中，用以测试的5个算法的最大迭代次数统一都设为1 000，每隔100代函数的定义域发生一次震荡，即环境总共经历10个周期，也即10次震荡。5个算法都包括100个个体（或粒子），初始化时所有个体都被安置在同一点（3，3）。5个算法都采用浮点数编码方案，且都运行100次，取平均值。计算结果如图1所示。

从实验结果可以观察到几个明显的现象：一是对标学习算法的动态追踪能力远强于其他4个算法，且其顽健性超强。可以看到，无论函数定义域如何变化，对标学习算法都能进行有效追踪，并且都能搜索到新空间内的全局最优解。二是对标学习算法的快速收敛能力很强。面对新环境，对标学习算法总是能很快收敛到全局最优解上。这是学习性竞争与竞争性学习思想有机融合的魅力。另外，这也与初始化时设置的种群及个体数量有关，数量越大，则全局收敛速度越快。三是在环境发生不同强度的震荡时，其他4个算法的搜索性能也同步发生了不同程度的震荡。这4个算法的动态优化性能，看似总体差别不大，但实际上彼此之间差异很大。从图1中可以看到，每个算法搜索到的最优解的路径与轨迹整体上比较平滑，那是因为它们是每个算法运行100次结果的平均值。可以观察到，其他4个算法的搜索性能是极不稳定的。

4.3 基于基因变形的动态函数优化

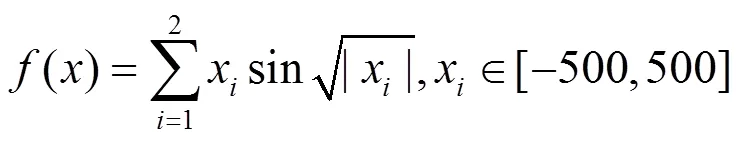
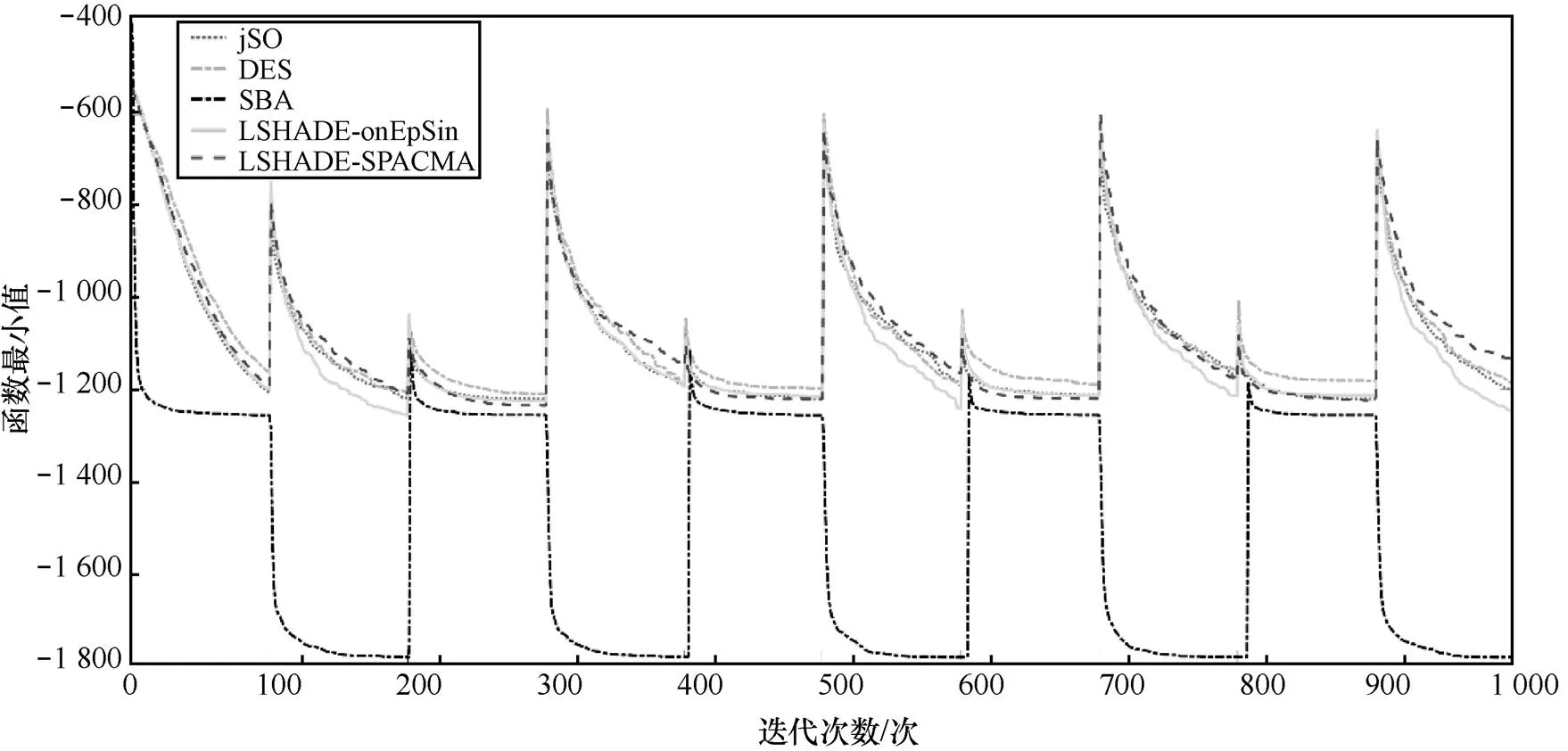
图1 基于空间变形的动态函数优化运行100次的平均值

在本次测试实验中，5个算法的参数设置与第4.2节实验完全相同。为保证公平公正，在本次实验中，用以测试的5个算法的最大迭代次数统一都设为1 000，每隔100代函数的定义域发生一次震荡，即环境总共经历10个周期，也即10次震荡。5个算法都包括100个个体（或粒子），初始化时所有个体都被安置在同一点(3,3)。5个算法都采用二进制编码方案，且都运行100次，取平均值。当环境变化强度（CR）分别为0.1、0.5、0.9时，5个算法对全局最小值的动态追踪轨迹如图2所示。

可以看出：一是对标学习算法的快速收敛能力较强，且其顽健性很强，远远优于其他4个算法。二是环境变化对算法具有显著的影响。可以看到环境震荡强度，从0.1增大到0.5时，5个算法的搜索结果都出现了强烈的震荡，从0.5增大到0.9时，其他4个算法的搜索结果的震荡程度都增大了，但对标学习算法反而减小了，这和它具有较强的保持种群多样性的能力有关。因为对标学习算法在运行过程能一直保持较好的种群多样性，在环境发生变化前夕，即所有个体基因在与模板做异或运算之前，有的个体本来离全局最优解的距离较远，同时因为环境震荡强度为0.9，即模板上有90%的基因值为1，于是那些本来较差的个体在与模板做异或运算时，其基因反而得到了改善。于是图2（c）中所示的算法在每一代的全局最优解，在搜索空间发生变形时，震荡反而不及0.5时剧烈。三是与基于空间变形的动态函数优化时类似，在环境发生不同强度的震荡时，其他4个算法的搜索性能也同步发生了不同程度的震荡，时好时差。

5 结束语

本文的核心贡献在于算法的“智能性”是体现在操作算子的组织策略而非概率规则上，这样就打破了需要依靠概率规则来平衡探索性与开发性的“潜规则”。从本质上讲，本框架不只是一个具体的算法，更是一种普适性方法论，它介于工程技术与认知哲学之间。因此它可以应用于科学、工程和管理中许多具体问题当中。

一般来说，元启发式搜索的设计是一类实验性科学，其大部分工作是基于模拟实验和实际应用的。这类算法的复杂随机性使得严谨的理论研究，尤其是计算复杂性研究难以实现。尽管已经提出了许多理论和方法来研究这类算法的计算复杂性和收敛性，但在理论界存在一些争议[8,9]。根据奥卡姆剃刀原则，本文抛弃了复杂的操作算子的概率调优规则，用一个简单的框架来组织核心算子，达到了许多组合算法的搜索效果。本文的目的是将企业管理中的标杆管理思想建模为单目标实参数优化问题的搜索方法。

[1] SÖRENSEN K. Metaheuristic-the metaphor exposed[J]. International Transactions in Operational Research, 2015, 22(1): 3-18.

[2] PIOTROWSKI A P, NAPIORKOWSKIJ J, ROWINSKIP M. How novel is the “novel” black hole optimization approach?[J]. Information Sciences, 2014(267): 191-200.

[3] FONG S, WANG X, XU Q, et al. Recent advances in metaheuristic algorithms: does the Makara dragon exist?[J]. The Journal of Supercomputing, 2016, 72(10): 3764-3786.

[4] BREST J, MAUČEC M S, BOŠKOVIĆ B. Single objective real-parameter optimization: algorithm jSO[C]//2017 IEEE Congress onEvolutionary Computation (CEC), June 5-8, 2017, San Sebastian, Spain. Piscataway: IEEE Press, 2017: 1311-1318.

[5] AWAD N H , ALI M Z, SUGANTHAN P N. Ensemble sinusoidal differential covariance matrix adaptation with Euclidean neighborhood for solving CEC2017 benchmark problems[C]//2017 IEEE Congress on Evolutionary Computation (CEC), June 5-8, 2017, San Sebastian, Spain. Piscataway: IEEE Press, 2017: 372-379.

[6] MOHAMED A W, HADI A A, FATTOUH A M, et al. LSHADE with semi-parameter adaptation hybrid with CMA-ES for solving CEC 2017 benchmark problems[C]//2017 IEEE Congress on Evolutionary Computation (CEC), June 5-8, 2017, San Sebastian, Spain. Piscataway: IEEE Press, 2017:145-152.

[7] JAGODZIŃSKI D, ARABAS J. A differential evolution strategy[C]//2017 IEEE Congress on Evolutionary Computation (CEC), June 5-8, 2017, San Sebastian, Spain. Piscataway: IEEE Press, 2017: 1872-1876.

[8] MICHALEWICZ Z. Quo vadis, evolutionary computation? On a growing gap between theory andpractice[J]. Lecture Notes in Computer Science, 2012: 98-121.

[9] MICHALEWICZ Z. The emperor is naked: evolutionary algorithms for real-world applications[J]. Association for Computing Machinery Inc, 2012(3): 1-13.

Intelligent optimization algorithm based on benchmarking

XIE Anshi

Zhejiang University of Technology, Hangzhou 310014, China

Many of the issues in scientific research, engineeringand management can be transformed into optimization problems. The various methods applied to these problems were a variety of models. Designing different methods was designing different models. The theme was to model the benchmarking philosophy in business management as a meta-heuristic search method for single objective bound-constrained real-parameter optimization problems. According to the principle of Occam’s Razor, many complicated operators and their probability tuning rules were abandoned and a simple framework was used to organize the core operators to achieve the effect of many composition algorithms.

intelligent optimization algorithm, exploration and exploitation, global search and local optimization, benchmarking management

N940，TP202

A

10.11959/j.issn.1000−0801.2018144

2017−08−01；

2018−04−05

浙江省哲学社会科学重点研究基地技术创新与企业国际化研究中心项目；浙江工业大学中小微企业转型升级协同创新中心项目；教育部人文社会科学基金资助项目（No.17YJC630011）

Research Fund from “Zhejiang Provincial Key Research Base of Philosophy and Social Sciences-Research Centre for Technology Innovation and Enterprise Internationalization”, Research Fund from “Collaborative Innovation Center for Transformation and Upgrading of Micro, Small and Medium Enterprises, Zhejiang University of Technology”, The Ministry of Education of Humanities and Social Science Project (No.17YJC630011)

谢安世（1983–），男，博士，浙江工业大学助理研究员，主要研究方向为管理与决策的认识论与方法论。