基于PSO的配电网分时电价定价决策模型

南京南瑞信息通信科技有限公司 陈功胜 潘 恒

1.引言

我国电力市场改革共经历了7个阶段[1]，如图1所示。

图1 我国电力市场改革的7个阶段

我国电力市场的运营模式从建国初的“政企合一”到而今的“配售分开”，特殊的电力市场运营模式决定于了电力工业发展的水平和特殊的社会环境。近年来我国电力工业得到了快速发展，以往的“电荒”现象得到了解决，甚至出现了富余，随着15年电改9号文的发布标志着我国电力市场迈入了新的阶段，竞争的引入使得电力市场的越发开放[2]，这对供电企业的电价机制的形成提出了挑战，电价合理调整可以降低电网的峰谷差，从而减小电网公司的调度费用，减少电网的运行成本，有利于供电企业的良性发展。

2.基于消费者心理学的用户响应分时电价的用电行为分析

2.1 用户响应行为分析

销售电价对用户的刺激同样有一个最小可觉差，当销售电价小于该最小可觉差时，用户基本上无反应；而当销售电价大于一个上限值时，用户将不再有更多的可转移负荷，响应能力趋近饱和[4]。用户对电价的反应可以用负荷转移率来描述，其示意图如图2所示。

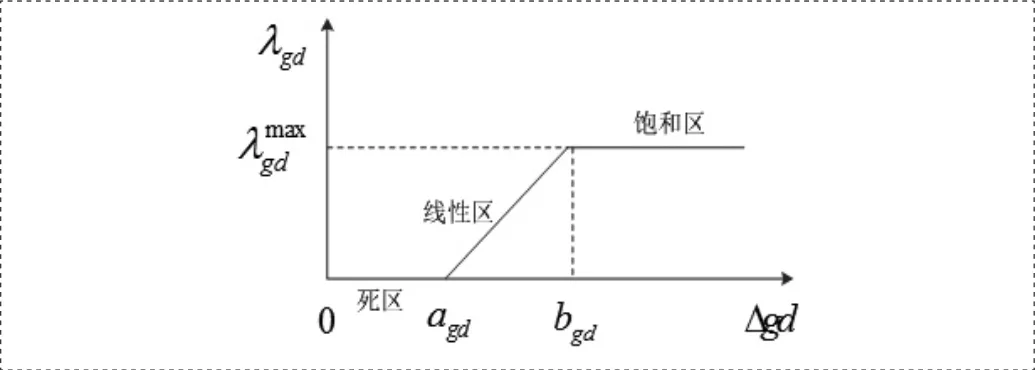
图2 负荷转移率

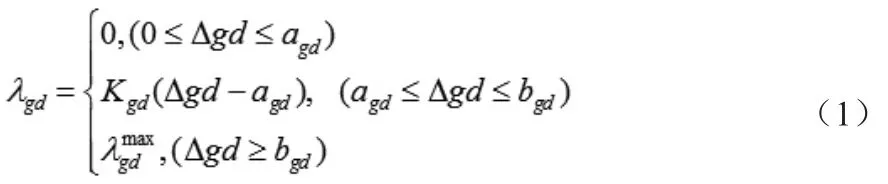
式中：

g、d分别为高电价和低电价，Δgd = g - d；agd、bgd分别为用户对电价差在死区与线性区的上限值；Kgd为线性区斜率。

假设对某地区所有签订了分时电价合同的用户，其负荷响应模型可用一组基于消费者心理学理论的折线表示，则可建立单一电价转变为尖峰电价后尖峰日的负荷响应模型。

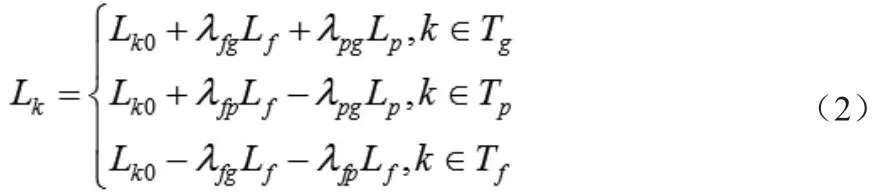
式中：

Tf、Tp、Tg分别为尖峰时段、平时段、谷时段；k为其中的任一时段；Lk0、Lk分别为分时电价实施前、后k时段的负荷； Lf、Lp、Lg分别为分时电价实施前峰、平、谷时段的负荷值。

3.配电网中分时电价定价决策模型

3.1 目标函数

供电企业调整电价机制的主要目标是优化电网的月度负荷曲线，减少电网的峰谷差，从而延缓电网投资，降低电网的调度费用，因此目标函数如下：

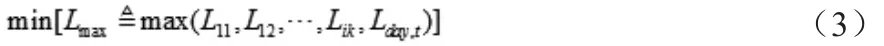
Lday,t为执行分时电价后第day天t 时刻点的负荷；Lmax为执行分时电价后该月的最大负荷。

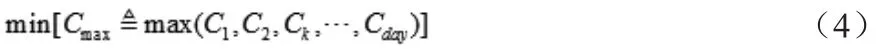
Cday为执行分时电价后后第day天的峰谷差；Cmax为执行分时电价后该月的最大峰谷差。

3.2 约束条件

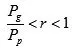
（2）峰时电价的取值不能无限制地上升，必须依靠政府相关部门对其进行监督和管制，假定峰时电价必须满足：

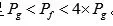
上述模型的待求解变量为尖峰日尖峰时段电价Pc以及非尖峰日电价折扣率r。该模型为非线性混合整数规划模型，并且目标函数具有一定的复杂性和求解难度，因此采用粒子群算法进行求解。

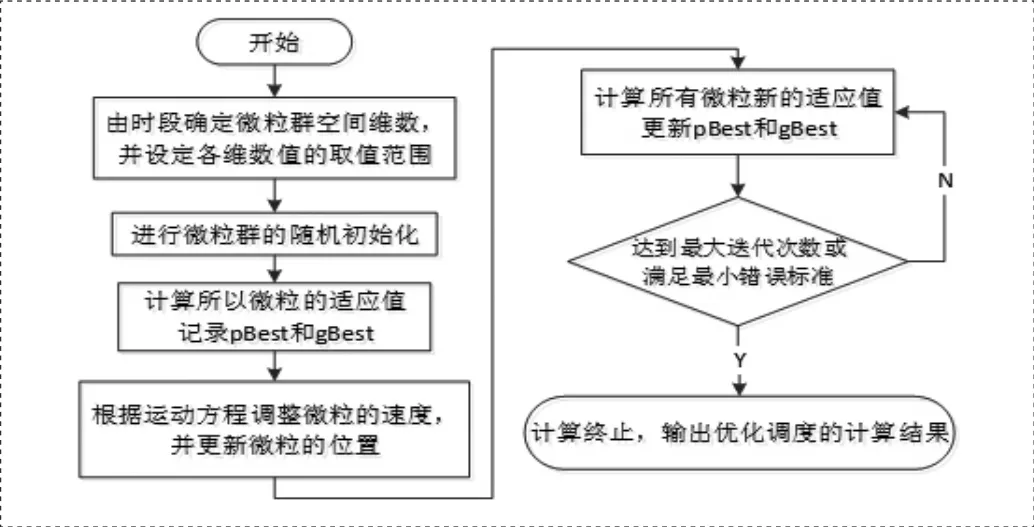
图3 PSO算法流程

3.3 基于PSO的算法实现

粒子群优化算法[粒子群算法及其应用研究（Particle Swarm Optimization, PSO）是一种群体智能算法[5]，本文利用粒子群算法进行求解分时电价的定价侧略，算法流程如图3所示。

4.算例分析

本文采用算例数据以某地区8月份负荷数据为基础，负荷曲线如图4所示。

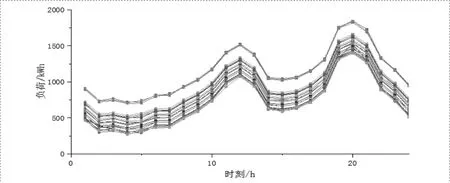
图4 某地区8月份负荷曲线

根据上图可知负荷的分布，将该地区的分时电价决策时段定为以下三个时段：

分时电价负荷转移率的相关参数设置如下表1所示。

表1 分时电价负荷转移率参数

采用粒子群算法求解，设平时电价为0.45元，谷时电价为0.22元，以峰时电价为待求解量，选取典型代表日负荷数据代入算法进行求解可得，最佳峰时电价为0.97元，执行分时电价前最高负荷为7944kWh ，执行尖峰电价后最高负荷为7669kWh ，减少了275kWh；执行分时电价之前电网最大峰谷差为2930kWh ，执行尖峰电价后最大峰谷差为2615kWh ，减少了315kWh。

5.小结

本文在对我国电力市场改革的几个阶段进行分析的基础之上，指出了电价机制调整的必要性，研究了基于消费心理学的用户响应电价的用电行为，以降低电网最高负荷和电网峰谷差为目标函数，采用粒子群算法进行求解，得到了合理的分时电价定价策略，对电网公司降低运行成本，提高竞争性具有一定的意义。