社区网的增长趋向及其分形特征分析
沈阳理工大学信息科学与工程学院 苑 勋 徐 野
东北大学软件学院 黄利萍
复杂网络是指具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络。复杂网络出现在各个学科领域,如生物学、物理学,甚至社会科学中。在过去的若干年中,许多关于复杂网络的规律被发现,如服从双向幂律分布的万维网,具有无尺度的特点艺人网络,呈现指数级衰减的送电网则。
本文通过研究一个社区网实例,确定社区网的分形规律,分析它的维数,做出奇异吸引子混沌轨道运动形式的数学模型,揭示其网络的复杂性及其在生长变化中的分形或混沌特征,确定预测模型的数学形式。
1.几个定义
定义1 社区网沈阳市某社区的全部业主,具有想建立联系想法的业主之间相互连接,组成业主为节点、相互联系为边的网络,称为社区网。
定义2 新增节点,社区网中新注册的用户代表的节点称为新增节点,一天内新增节点数用Nb表示。
定义3 增联节点,社区网中已注册用户若增加至少一个连接称为增联节点,一天内的增联节点数用Ns表示
定义4 眠联节点,社区网中的已注册用户一天之内连接保持不变称为眠联节点,一天内的眠联节点数用Nd表示。
定义5 觉联节点,社区网中的眠联结点如果一天之内至少增加一条边则称为觉联节点,一天内的觉联节点数用Na表示。
定义6 规模增速,设社区网中节点数为N,社区网规模增速r可用下式表示:

2.模型
2.1 让模型体现社区网的震荡性
由定义2~6及和 (1),我们计算社区网的规模增速r,通过观察计算得出的三周内节点增长速率图可知:社区网规模增速在不断地震荡。从肉眼观察可以看出震荡曲线表现出一定的周期性特点。因为震荡的曲线可以用不同周期的正弦余弦函数及其组合表示,所以可以将r转换为(2)来表示。
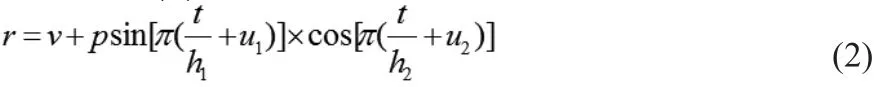
其中v为总体偏移量,p为振幅。h1、 h2为震荡半周期,单位为天。u1、 u2为震荡幅角。
把式(2)中r的表示代入Logistic模型,就是本文对Logistic模型的进一步修改,使其能够表示周期性的变化。
2.2 求解r表示式的系数
下面采用浮点型遗传算法求解r表示式的系数。
首先定义遗传基因,一个基因中包含了所有r表示式中的待定参数如(3)所示:

(2) 生成最初的基因群体,即若干组r表示式中的待定参数。本文中基因群的基因数为N=100,每个基因的编码值由随机算法生成。
(3) 匹配度估计函数
由基因编码确定的参数值计算出的r(t)应当与采样值r*(t)越接近越好。我们用社区网25天的采样数据来计算r(t)与r*(t)的差,由此得到匹配度估计函数。

利用匹配度估计函数计算每个基因编码(即每组参数取值)的分数,该分数为匹配度估计函数的倒数,即:

(4) 挑选优秀基因
设有随机数m(0<m<1),挑选分数比m高的前w个基因作为进一步繁殖的种群。为简化计算,复制选出的w个个体,删除按分数排序的后w个个体,保持种群个体数不变,进行下一步的繁殖。
(5) 杂交
繁殖种群个体数设为N,设MP=(x1…xi…xj…xn) 为杂交池中,用随机方法从中选择xi、xj两个基因进行杂交[10],基因中每个参数的杂交方式类同,如在参数v上进行杂交,公式为

按照上述杂交操作,对每个基因中的每个参数进行修正。修正的同时要防止参数衰减到0,当其值小于0.01时,设置为0.01。
(6) 变异
对杂交的到的N个基因中的每个参数进行变异,变异概率为0.3。参数v 的变异算法公式如下:

(7) 结束判断
本文采用双重结束判断算法,一个结束判断条件是(为结束时达到的分数下限,在本文中采用0.1作为下限);另一个结束判断条件是遗传算法的循环次数,如果循环次数达到上限,结束计算,不管此时score是否越过下限s。本文中设定的循环次数上限为1000,实验表明循环次数达到这一数值可以保证产生优良的后代。
2.3 拟合结果与评价
2.3.1 收敛分析
经过1000次遗传算法的循环,得到的最优基因(参数组),代入社区增长模型的结果如式(8):
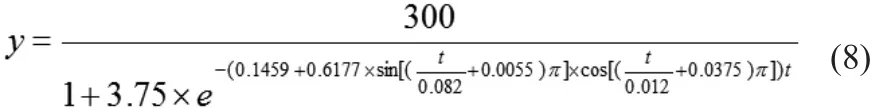
由此可以从图上看到100次循环以后,遗传基因达到最优,其后900次循环中,基因的分数变化不大,所以可以认为该遗传算法收敛,得到的结果较好。
2.3.2 拟合精确度分析
本文定义相对拟合误差ε,据此分析模型的拟合程度。定义7 设社区网规模采样数据原始值为y*(ti),用拟合模型计算出的值为y(ti)(i³1,iÎN),则相对拟合误差ε定义为误差和的均值占原始数据均值的比重,公式如下:
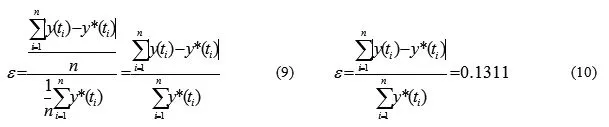
其中,i, n(n=25)表示采样天数为25天,每天采集一个数据。采用平均误差占平均原始值的比重表示相对的误差程度。
由式(9),可以计算出25天内社区网规模的相对拟合误差,故社区网规模增长模型的拟合精确度为1-0.1311=86.89%,结果较好,可以接受。
3.社区网规模增长的混沌分析
3.1 社区网规模增长曲线
由前面所述的社区规模增长的数学模型可以做出如图1的增长曲线。
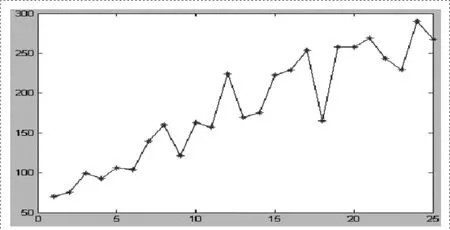
图1 增长趋向图(x轴-增长时间/天,y轴-网络节点值)
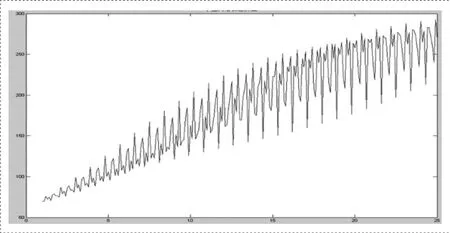
图2 增长趋向图(x轴-增长时间/0.1天,y轴-网络节点值)
从图1可以看出,社区网规模震荡向上走高,曲线呈现锯齿状,不光滑。为了表明曲线的特点,便于观察,我们将图中时间单位由1天变为0.1天,再次绘图得到如图2的曲线。
我们得到图2的曲线显示社区网规模曲线是一条连续向上增长的波动曲线,曲线仍然呈现锯齿状,在每个取值点都不可导,表现出混沌分形的特点。下文我们计算这一曲线的维数。
3.2 维数的计算方法
计算社区网规模增长的维数,首先取得采样时间序列,将一维的数据转换成m维数据,m依次取值为2,4,8,10,15,18等等。然后根据表2的计算方法,对每个m值计算相应的D2值,D2就是m的关联维数。如果随着m的增大,D2收敛于某一饱和值,说明社区网规模增长系统具有混沌分形的特点。反之如果D2不随m增大而收敛,而是趋向于无穷,则系统不具有混沌性。表2说明了与m相关联的维数D2的计算方法。

表2 计算时间序列的关联维数算法
3.3 社区网规模增长系统的维数
采用表2的算法,对m=2,4,8,10,12,15,18,20 计算r和cr,绘出ln(r)-ln(cr)曲线,从图中可以看出,m=12,15,18,20时曲线的直线部分具有平行性,它们的斜率基本相同,其斜率就是D2(关联维数),该值收敛。计算可得:

由以上计算可知社区网规模增长系统具有混沌分形特性,其关联维数是在2和3之间的分数维。
3.4 社区网规模增长系统的长期预测
根据文献,维数为D2的分形混沌系统,设D2向上取整的值为D,则至少需要D个方程描述系统中D个重要的物理规律,才能实现长期较准确的预测。
由式(12),社区网规模增长系统的关联维数为2、3之间的分数维,为了对该系统进行长期预测,至少需要3个方程为其系统建模,公式如下:

式中x,y,z为表达社区网系统重要物理规律的物理量,x(n)为x的n阶导数,y(n)为y的n阶导数,z(n)为z的n阶导数,n=1,2,3…。
式(13)表达了社区网混沌系统内在的运动规律,由于本文中采样数据较少,不能够确定f1~f3中的具体参数,因而将这部分计算作为我们下一步的工作。
4.小结与展望
因为Logistic模型有效反映了有限资源条件下生物种群增长的规律,和社区网络具有内在相似性,本文采用Logistic模型为社区网落规模增长趋像建立了数学模型。因为社区网规模在震荡中增长,本文增加了模型中的三角函数因子,改进了原模型,是其能够反映震荡特性,模型参数用遗传算法进行搜索,得到较为优异的拟合值。
模型曲线连续但不可微,呈现锯齿状,表现出混沌分形特性,本文利用维数计算方法计算得到了社区网规模增长系统的维数为2.062。维数计算收敛,表明社区网规模增长系统中混沌分形性是真实存在的。
最后本文指出要对社区网规模增长系统进行长期较为准确的预测,必须至少采用三个以上的物理量及其多阶导数的三个以上的方程式描述内在的重要物理规律。本文给出了上述数学模型,我们下一步的工作便是求解模型中的参数。

