超高层钢结构建筑倾斜性监测分析

朱 赞，甘 淑

(昆明理工大学 国土资源工程学院，云南 昆明 650093)

钢结构建筑尤其是超高层钢结构为主体的建筑物安装和施工是一个极其复杂且精密的过程。在其施工过程中由于重力载荷、温度载荷、风载荷以及基础形变[1]等因素的影响，往往会出现建筑物的结构变形和整体倾斜变形。首先，结构变形会使得构件的实际位置偏离设计的安装坐标，对后续的施工安装工作造成极大影响。其次，在超高层钢结构尤其是塔式超高层钢结构建筑的施工中，建筑物的倾斜变形量过大不仅会造成工程质量问题，甚至造成重大安全事故。因此，如何有效地对其进行倾斜变形监测并控制其倾斜量成为此类工程中的一大难点。

高层建筑物的倾斜变形主要由结构自重、风力大小与风向、温度变化、地基沉降等因素的影响而产生[2]。一般而言，伴随着施工过程的进行，点位的位移随时间大致呈线性变化[3]，且越到高层则建筑的累计变形量和变形速率的变化越大。CCTV新台址主楼是目前国内最大的单体钢结构建筑[4]，由于建筑造型独特，该工程的变形监测工作在同类建筑中具有一定的代表性。刁建鹏等[4-5]采用最小二乘拟合构建施工进度与建筑累计变形量之间的关系模型准确反映了塔楼的变形规律，且通过对建筑的日变形规律与气温变化规律进行对比分析，揭示气温变化对建筑结构变形的影响，最终为悬臂的安装决策提供技术支持。此外，文献[5]着重对该建筑施工过程中的建筑高度与倾斜变形量二者之间的关系进行分析，得出倾斜变形量与建筑高度和时间呈线性关系的结论，为施工过程中变形量的预测提供依据。文献[6]将最小二乘回归模型运用到混凝土重力坝变形监测中，并在对变形量的预测过程中取得良好的效果。文献[7]将时间序列分析应用于地铁变形监测的数据分析中，为施工过程提供更为准确的技术参考。本文以工程实践中所进行的某超高层钢结构建筑实测数据为依据，通过趋势分析法构建倾斜变形量与时间、变形速率与高度的回归分析模型，相对准确地掌握建筑物的倾斜变形规律。通过对温度变化与建筑变形速率进行对比分析，以此探讨二者之间存在的关系，从而为施工和构件安装提供参考依据。

1 监测方案布设实施

某建筑纵剖面及其监测点布设如图1所示。待监测建筑物高度为162.5 m，地面部分34层，地下部分2层，其中-2至4层外部为钢筋混凝土结构，内部主干架与4至34层连成一体，为主体钢结构。监测网采用安装独立坐标系，由G1，G2两个基准点组成，两点均在施工区以外的稳定区域。基准点每周与原安装坐标系基准网联测一次，并对其进行稳定性分析。建筑物监测点位的布设自建筑第6层开始至第32层，每隔4层布设一组监测点，其中第12层增设一组点位。每组3个监测点，分别位于建筑的每层房角位置，分别命名为A，B，C系列，监测点位命名规则为建筑层数+系列号。

图1 监测点布设示意图

观测采用Leica TM30精密监测机器人进行。每周一至周六观测时段选择为下午16：00—18：00，以保证将温度、光照等因素对观测成果的影响降到最低。观测频率为每隔15 min自动观测一次，并取多次观测平均值作为观测成果。此外，为监测建筑物的日变形规律，每周日进行一轮连续观测，观测时间为当天早6：00至次日早8：00，共计26 h，观测间隔为15 min。数据预处理采用仪器自带处理软件进行。

2 累计变形量与时间关系分析

对某监测点位连续观测一段时间，并通过回归分析模型(3)对点位的累计变形量(Δi)与累计观测时间(t)这一对变量进行线性回归分析构建其一元线性回归方程。这里以监测点位F24C为例，选取一个累计观测时间为142 d的样本，其中剔除风力超过2级、阴雨天气、气温>30 ℃且<17 ℃的天气所观测的数据，剩余样本数共计46个。对该样本构建回归分析模型如图2所示。

(1)

图2 F24C点变形量与时间回归分析图

如图2所示，F24C点X，Y，Z的累计变形量Δi与累计观测时间t之间的回归直线方程为

Δx=0.34t+6.84，

Δy=-0.29t-4.31，

Δz=-0.29t+5.08.

(2)

分别对累计观测时间与X，Y，Z坐标的累计变形量3组数据的回归模型进行r检验，取显著水平α=0.01。查表可得r0.01(n-2)=0.290 4，通过计算可得|rΔx|=0.928 9，|rΔy|=0.953 9，|rΔz|=0.946 8，即|rΔx|>r0.01(n-2)，|rΔy|>r0.01(n-2)，|rΔz|>r0.01(n-2)，因此可认为3组数据线性关系均显著[8]。

(3)

通过对A，B，C系列所有监测点分别做累计变形量与累计时间的回归分析模型，并进行比较后，可发现该建筑物在X方向上的变形为正，而在Y和Z方向上的变形为负。联系监测坐标系的北方向为正北方向，可得出待监测建筑物总体呈现出平面上在X方向上朝北偏移，在Y方向上整体朝西偏移，在Z方向上发生沉降。

3 变形速率与高度的关系分析

根据该建筑外形为近似标准四棱柱的特点，且A,B,C3个系列的监测点分别位于建筑四角的3根柱子上。则可通过对A,B,C3个系列的监测点变形速率与高度进行回归分析，从而构建这两个变量的回归直线方程，并由此可分析出该建筑物倾斜变形规律。这里以C系列点位的8组监测数据为例，变形速率v与所处高度h的回归分析如图3所示。

图3 C系列变形速率与高度回归分析图

C系列监测点X,Y,Z方向变形速率v与点位高度h回归直线方程为

vx=0.002 8h+0.001 8,

vy=0.002 3h+0.017 3,

vz=0.002 2h+0.030 1.

(4)

4 倾斜性分析与温度影响讨论

4.1 倾斜性分析

通过以上对该建筑各监测点位累计变形量Δi与累计观测时间t的回归分析，以及对3个系列点位变形速率v与监测点高度h之间的回归分析，构建得出数学模型如式(2)与式(4)。最后，统计整理得出的A，B，C系列监测点位的变形速率变化率状况如表1所示。

通过对表1中的数据进行分析可知，就平面位移变形而言，B系列点位变形速率及震荡幅度最大，可判定为不稳定，C系列点位变形速率及震荡幅度较小，可判定为稳定。就沉降变形而言，C系列点位变形速率较大，可判定为不稳定，同理，A系列点位可判定为稳定。

表1 变形速率变化率统计表 mm

此外，根据3个系列点位各自施工阶段的最后一期监测数据与首期观测数据的对比可以分别计算出其累计变形量，由于建筑主体横截面为标准矩形结构，理论上建筑物变形后横截面仍然遵循平行四边形原理。因此，可由位于建筑3个角落的A，B，C3个系列的监测点位位移量拟合出第4个建筑角点的位移量。将位移后的实际位置与设计位置进行对比，如图4所示。

图4 中心轴线水平位移情况示意图

另外，考虑到由于该建筑的主轮廓线为矩形，可将建筑物横截面的几何中心点视为建筑中心轴线位置，通过对建筑设计中心轴线位置与监测结果中的中心轴线位置进行对比可计算出中心轴线的平面累计偏移方向为西偏北32°12′43″，偏移量为89.3 mm，通过式(5)可计算该建筑实际中心轴线与设计中心轴线的偏移角度α。

(5)

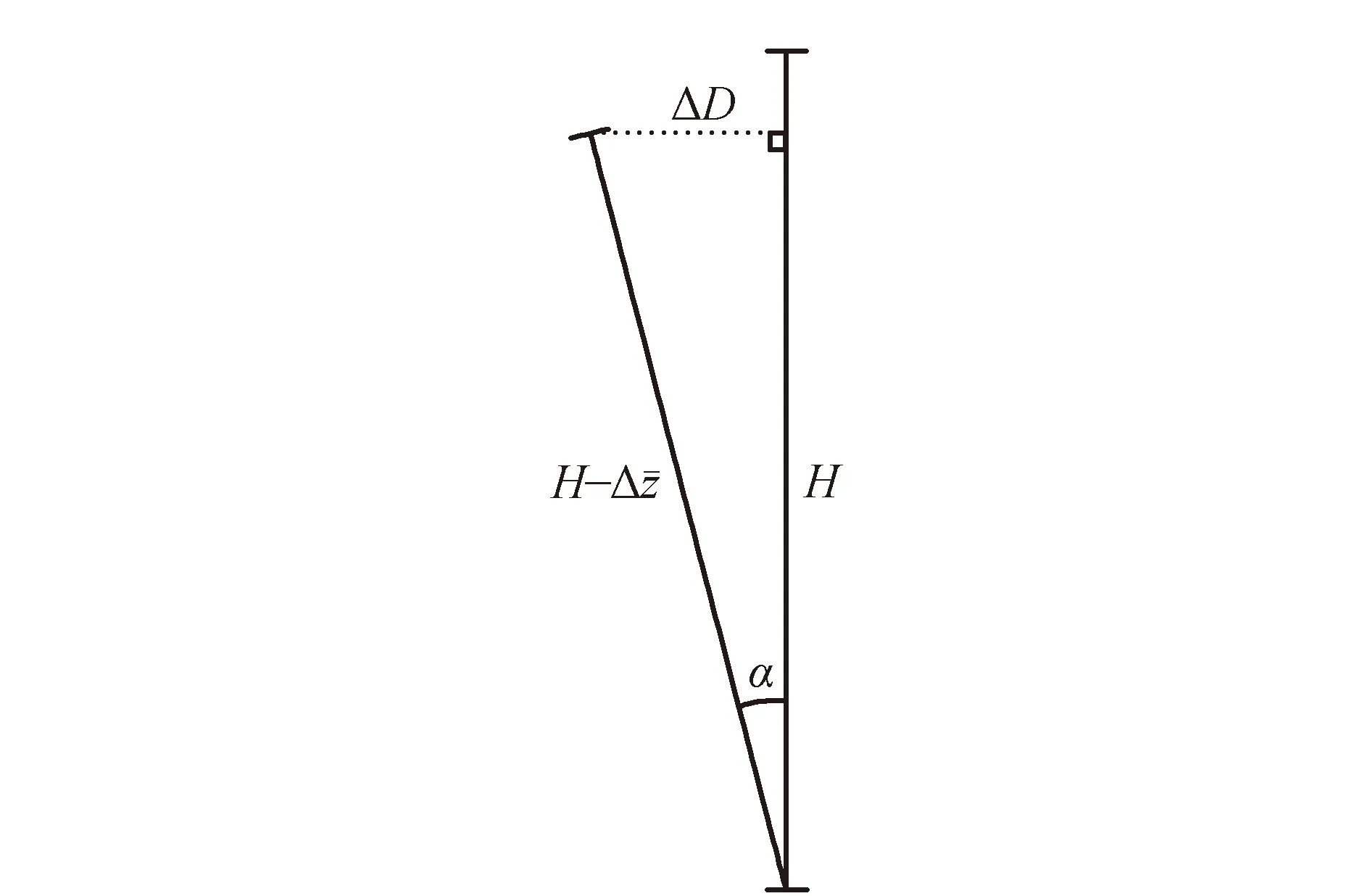
图5 中心轴线偏移角度示意图

4.2 温度影响分析

在钢结构建筑的施工中，温度载荷是导致主体结构产生变形的重要因素之一。相对准确地掌握温度变化与建筑物变形之间的规律是整体控制建筑物倾斜性的重要方法。[10]本文通过分别选取位于建筑物16层的3个点位(F16A、F16B和F16C)在2014年3月16日早上6：00至次日早上8：00的连续26 h观测数据作为样本，并同时监测该日的气温变化。当日不同时段温度变化情况如图6所示，同时刻3个监测点的X,Y，Z3个方向的变形量平均数变化趋势如图7所示。

图6 施工区域日气温变化情况

图7 16层3个点位日平均变形趋势图

如图6所示，根据对单日气温变化趋势的分析可将单日气温变化分为3个阶段：匀速上升阶段、快速上升阶段和缓慢下降阶段。同理，如图7(a，b)所示，通过对所选样本数据单日变化趋势进行分析，可发现建筑物的变形量在一天中不同时段的变形量呈现出一定的规律性，即在X，Y方向上，当日早上约8：00至中午约11：30，建筑变形速率较大；中午11：30至次日早上约6：00，建筑物的变形呈缓慢恢复趋势；次日早上6：00至8：00，建筑物变形呈匀速恢复趋势。根据对以上特点的分析，可将钢结构建筑的单日平面位移变形分为3个阶段：快速变形阶段、缓慢恢复阶段和匀速速恢复阶段。如图7(c)所示，建筑Z方向上的变形在局部时间内出现较大波动，以下午约16：00为分界线，早上和中午波动较大，晚上和凌晨波动较小。结合施工现场情况分析，这主要是由于白天施工过程中产生的撞击和压力所引起的局部时间段内建筑物的较大震荡。此外，就整体而言，该建筑物在Z方向上的变形速率均匀，可知温度对该建筑的垂直方向变形影响较小。为探究温度与变形量的关系，这里分别对单日气温变化和平面的单日变形量的3个阶段所处时间段进行对比如表2所示。

如表2所示，对建筑物在X和Y方向上单日变形的3个阶段起始时间和结束时间进行对比可发现在当日上午气温的快速上升时段，建筑物的水平方向变形也处于快速变形阶段；同样，当日下午、晚上至次日凌晨，气温在缓慢下降阶段，建筑物水平方向的变形处于缓慢恢复阶段；次日早晨气温缓慢上升，建筑物水平方向变形处于快速恢复阶段。通过以上分析可知该钢结构建筑物水平方向变形速率随着气温变化速率的增大而增大，二者之间具有紧密联系性。

5 结束语

本文通过对某超高层主体钢结构建筑进行连续观测，并对不同高度监测点的位移和沉降量进行分析，构建累计变形量Δ与累计观测时间t、变形速率v与监测点高度h两对变量之间的函数关系。通过统计检验方法判定其具有显著的线性关系。引入变形速率变化率(v/h)的概念，通过对不同方位的3组监测点的变形速率变化率的比较分析可得出B系列监测点对应的建筑方位在水平方向上较不稳定，而A系列对应方位的沉降速率较不稳定。之后，通过对各监测点的变形量拟合计算出建筑中心轴线的偏移量以及偏移方位和角度。还通过对监测点位的日坐标位移变化与当日气温变化进行对比分析，揭示建筑物的变形速率与气温变化速率之间有一定的关联性和周期变化性，即温度变化速率越大则钢结构建筑的变形速率越大。其中，以早晨7：30至中午11：30左右变化最为显著，结合图7(c)分析的结果：当日早晨6：00—16：00前建筑物整体震荡幅度较大，16：00之后至次日早晨6：00震荡幅度较小。因此，为避免因变形速率较大而造成各杆件连接部位的损伤，重要构件的安装时间不宜选择在下午16：00之前。而应选择在当日傍晚至次日凌晨之间，该时间段建筑的整体变形速率较低，对新安装的构件有足够的预应力缓冲时间。此外，由于不同季节的日气温变化呈现不同规律，则超高层钢建筑重要构件的安装时间可根据气温的日变化规律进行决策。

表2 单日气温变化与平面变形量变化时间段对比