HELICAL SYMMETRIC SOLUTION OF 3D NAVIER-STOKES EQUATIONS ARISING FROM GEOMETRIC SHAPE OF THE BOUNDARY∗
Weifeng JIANG(姜伟峰)
School of Sciences,Department of Mathematics,Wuhan University of Technology,Wuhan 430070,China
E-mail:weifengjiang@163.com
Kaitai LI(李开泰)
School of Mathematics and Statistics,Xi’an Jiaotong University,Xi’an 710049,China
E-mail:ktli@xjtu.edu.cn
Abstract In this article,we investigate three-dimensional solution with helical symmetry in a gap between two concentric rotating cylinders,inside is a helicoidal surface(screw propeller)while outside is a cylindrical surface.Establish the partial differential equations and its variational formulation satisfied by a helical solution in a helical coordinate system using tensor analysis method,we provide a computational method for the power and propulsion of the screw.The existence and uniqueness of weak helical solutions are proved.
Key words Navier-Stokes equations;helicoidal surface;rotating helical flow
1 Introduction
It is well known that there are many solutions with very simple spatial symmetries for the Navier-Stoke equations,for example,axially-symmetric flows,particular in pipes of circular cross-section,in the domain between two rotating cylinders.Frequently,axially-symmetric flows first lose stability at a point of bifurcation in which the axial symmetry is broken,with the bifurcation solution lying in what one call the a class of helical solutions to the Navier-Stokes equations.
In cylindrical coordinates(r,θ,z),the velocity u and pressure in helical flows do not depend upon θ and z independently,but only on the linear combination nθ+ αz,where n and α take assigned integer and real value,respectively.Thus,a two-parameter(n,α)family of flows is defined.This family is in some sense the next most complex class beyond axially-symmetric motions.Nevertheless,this class remains essentially two-dimensional,but it is called“2D-3C flow”.
It is well known that for the Navier-Stokes equations in three dimensions,it is not known whether weak solution is unique or whether a strong solution exists for an arbitrary time t.For the system of Navier-Stokes equations on the plane,on the one hand,existence and uniqueness results are available(see,for example,[2,5,7,9,12,13]and references therein).On the other hand,in[11],it proved uniqueness of weak solution and these weak solutions are,in fact,regular solutions existing for arbitrary time t;the global attractor for the in finite-dimensional dynamical system generated by the corresponding semi-group of helical flows to be compact and connected;estimate the Hausdorff and fractal dimensions of the global attractor in terms of the parameter of the problem.
In this article,our goal is to study helical flow driven by rotating boundary with helicoidal surface in a domainbounded by an inner rotating screw propeller and an outer in finite cylindrical surface with radium r1>0.
Describing this helical flow in view of tenor analysis methods different by using other method in[8]and references therein.We also study on the weak solution and strong solution of Navier-Stokes equations in helical coordinates.
This article is organized as follows.Describe centric helical surface and helical coordinate system in Section 2 and Section 3.Same operations are formulated in Section 4.In Section 5,we establish the Navier-Stokes Equations in helical coordinate.In Sections 6 and 7,we provide the partial differential equation governing helical symmetric solution and its variational formulations;In Section 8,we derive for mulae of the power and propulsion of the screw;In Section 9,we consider the eigenvalue problems of helical Stokes flow.In Section 10,we prove the existence and uniqueness of helical solution and give a Fourier-Finite element approximation solution.

Figure 2 Helicoid 2
2 Centric Helicoidal Surface
It is well known that a positive helicoid surface ΣHis a smooth immersion ℜ :R2→ R3defined by

The metric tensor aαβof positive helicoidal surface ΣHin Gaussian coordinate(ξ1,ξ2)is given by

The contravariant components of metric tensor are
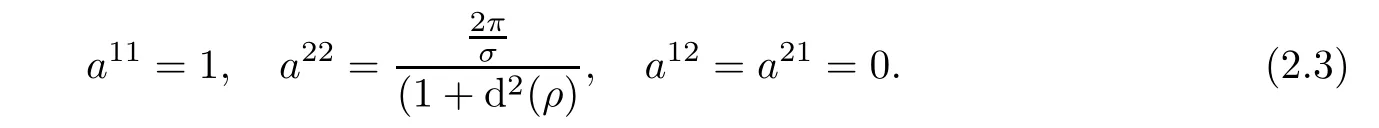
In addition,the covariant components bαβof curvature tensor of ΣH(that is,coefficients of second fundamental form of ΣH)are

Mean curvature and Gaussian curvature are given by
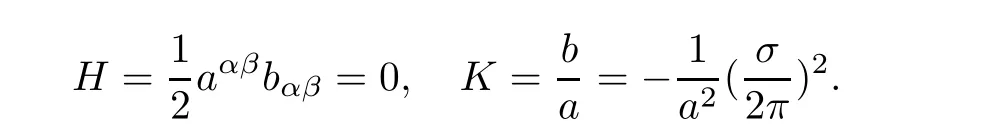
Let(yi,i=1,2,3)denote Cartesian coordinates and introduce a helical symmetry group
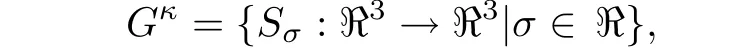
where the transformation Sσ(S stands for“screw motion”)is defined by
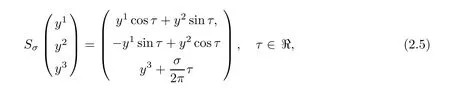
which is a superposition of a simultaneous rotation around the z axis with a translation along the z axis.The symmetry lines(orbits of Gκ)are concentric helices.Invariant curves for the action of the helical group Gσare helices having z=y3axis as axis of symmetry.In particular,action of Sσon the helicoidal surface ΣHdefined by(2.1)shows

3 Helical Coordinates
Let us establish “helical coordinates system” {xi′}which is defined by
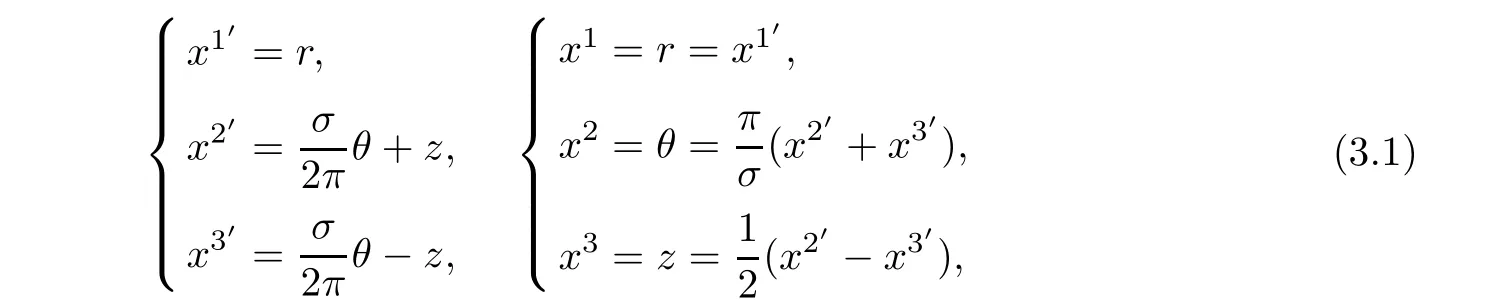
where constant σ >0 is periodic step,and{x1=r,x2= θ,x3=z}is a cylindrical coordinates system.(y1,y2,y3)denote Cartesian coordinate,which can be expressed in terms of helical coordinates
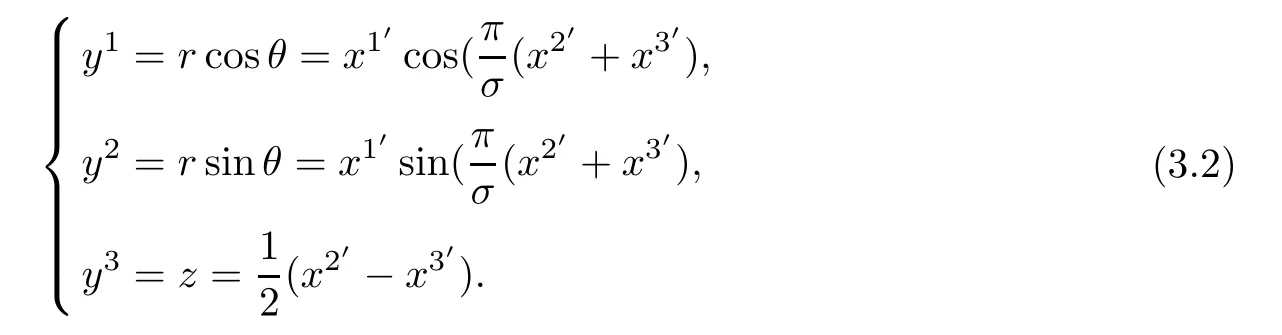
By(2.1),the equations of positive helicoidal surface ΣHin helical coordinates are given by
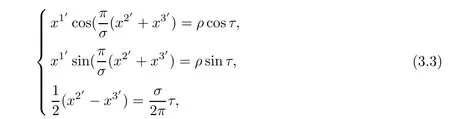
where(ρ,τ)are parameter,the Gaussian coordinates on ΣH.From(3.3),we obtain equations of ΣHin helical coordinates

This shows that the equations of ΣHin helical coordinates are given by
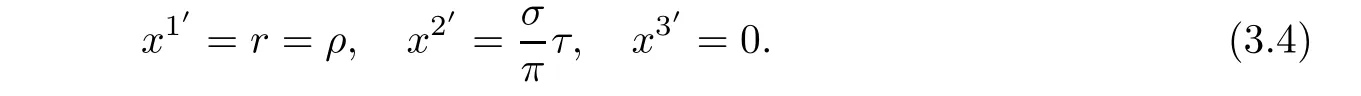
In other word,x3′=0 coordinate surface in helical coordinate system is a helicoidal surface while x1′=constant corresponds cylindrical surfaces.
Proposition 3.1In the helical coordinate(xi′,i=1,2,3),x3′=0 corresponds with a helicoidal surfacecan be chosen as Gaussian coordinates on ΣH,corresponding equations describing ΣHare given by

The associated metric tensor aα′β′of ΣHin Gaussian coordinate(ξα′,α′=1,2)are given by

where ξ1= ρ, ξ2= τ are defined by(2.1).The curvature tensor bα′β′of ΣHin(ξ1′.ξ2′)are given by
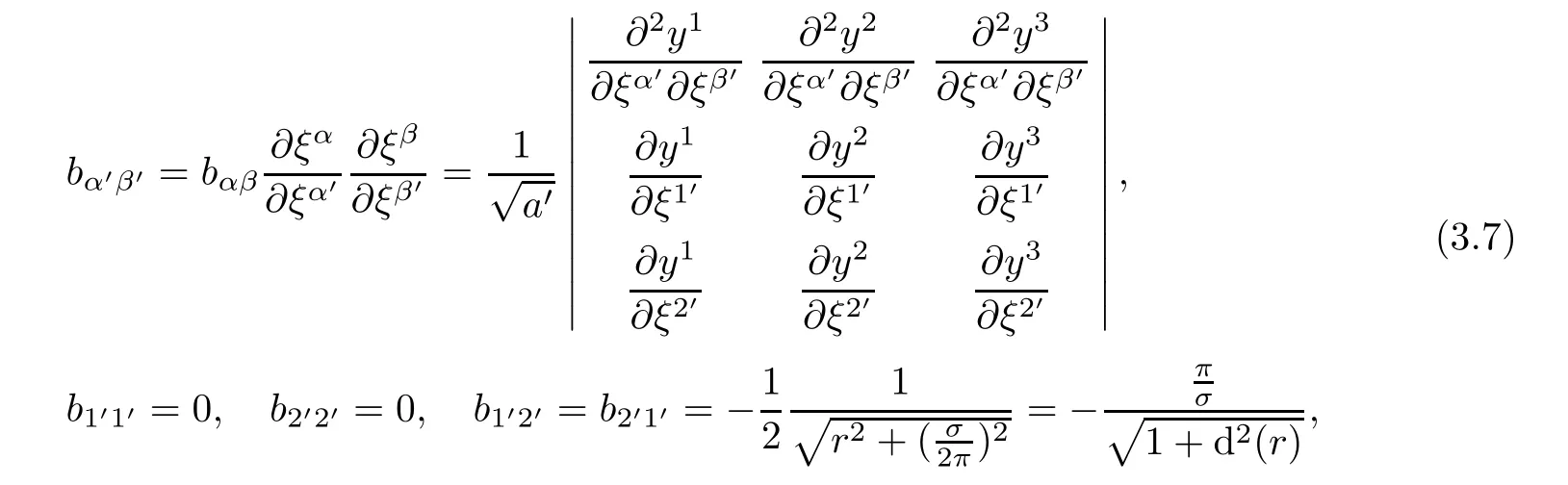
where

ProofIt is enough to prove(3.6)and(3.7).Indeed,because transformation of Gaussian coordinatessatisfy

together with(3.4),it yields
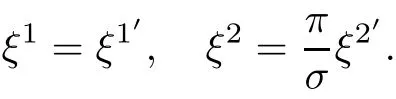
Hence,
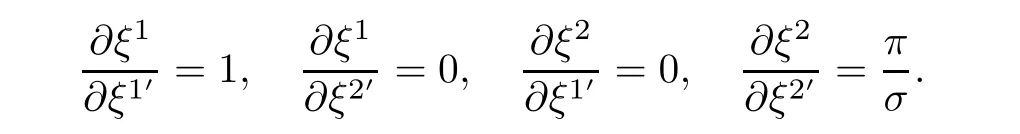
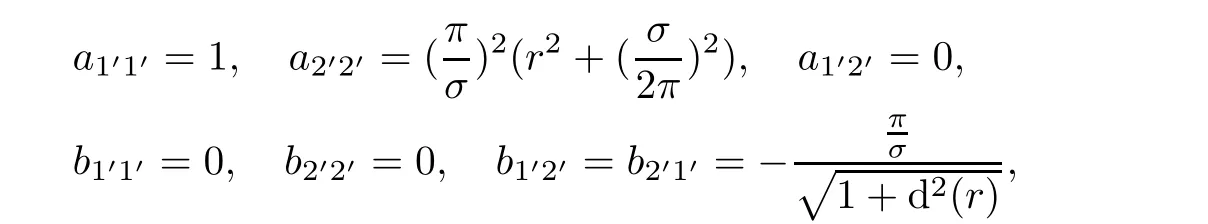
which yield(3.6)and(3.7).On the other hand,taking(3.5)into account,we obtain the following formulae:
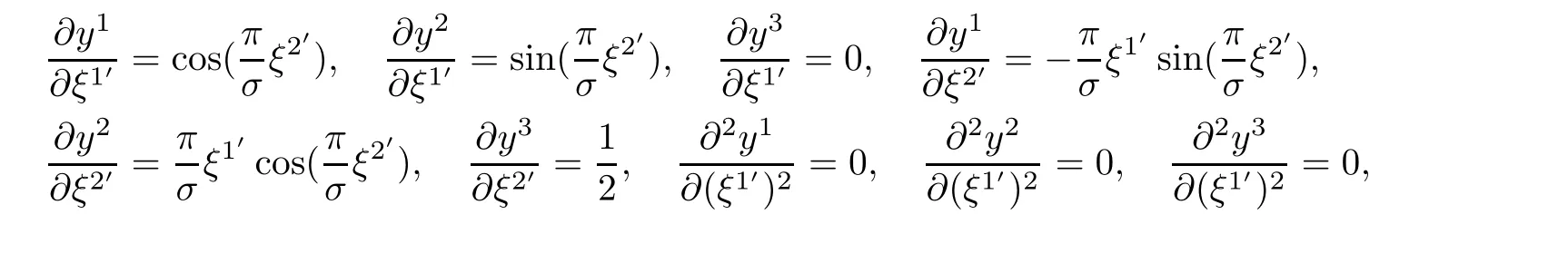
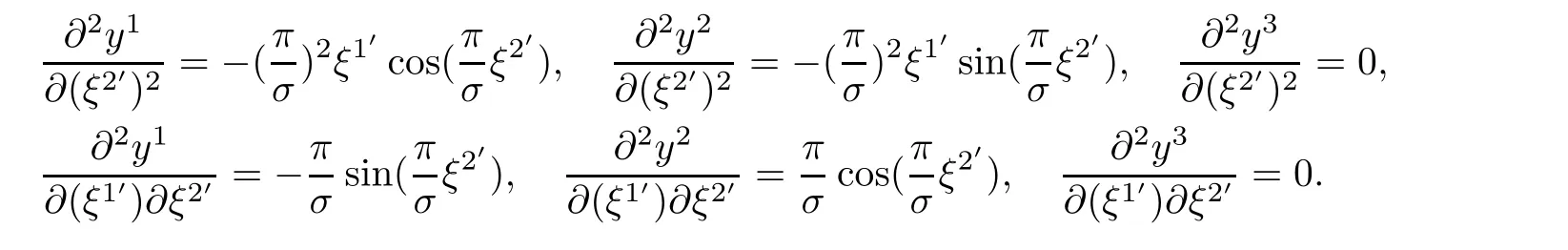
Then,
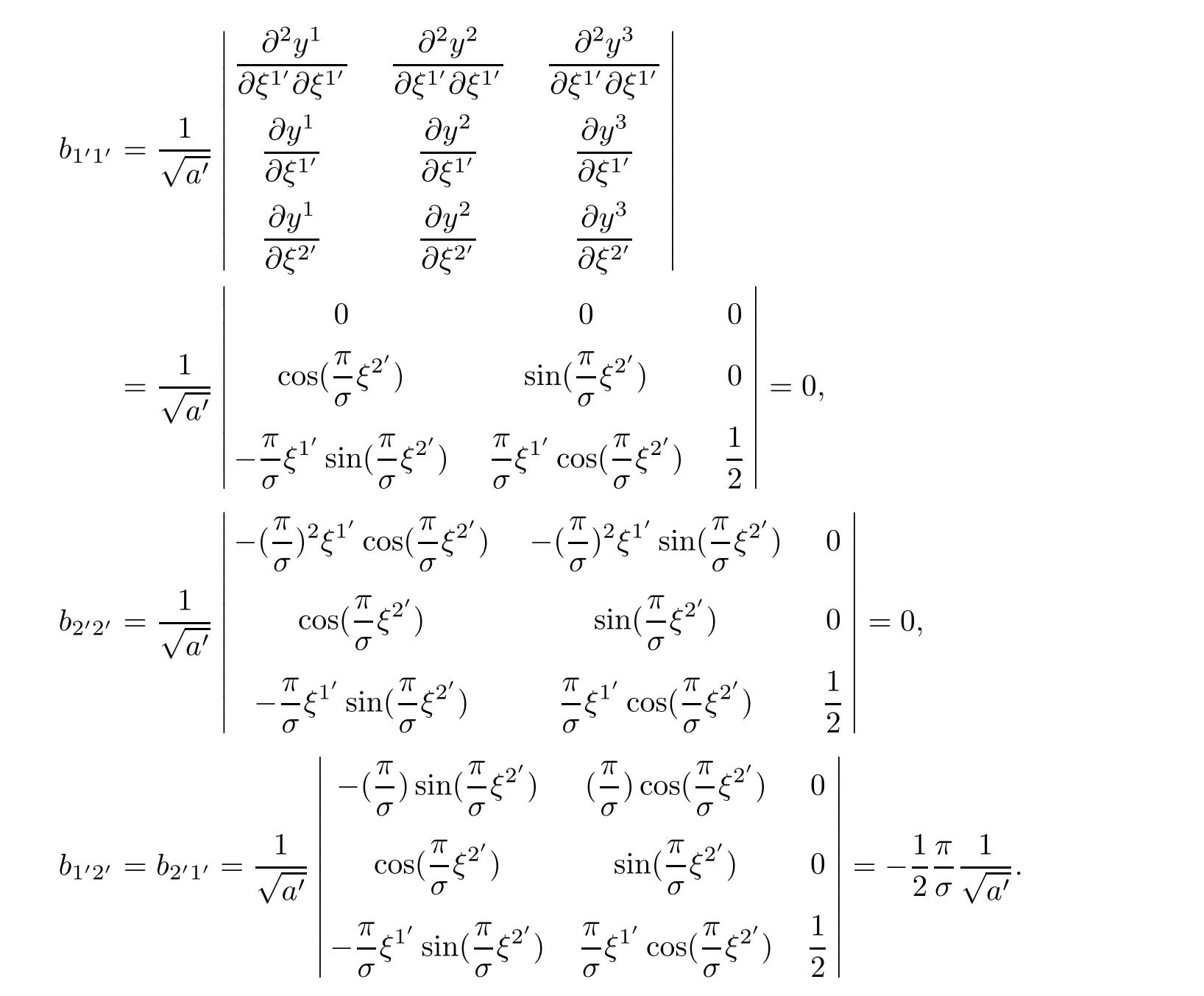
These coincide with(3.6)and(3.7).Thus,the proof is complete. ?
Coordinate transformation between helical coordinates and cylindrical coordinates can be expressed as


Let u denote the velocity of the fluid,the contravariant components of velocity vector in helical coordinates system and cylindrical coordinates system expresses respectively
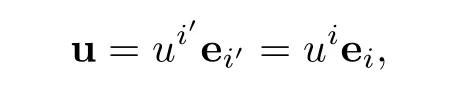
where ei′are base vectors of helical coordinates system
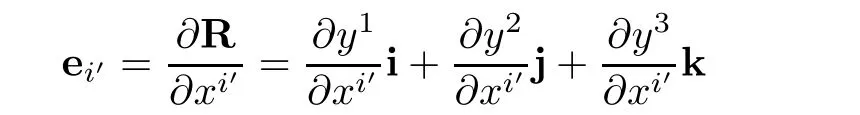
and eiare base vectors of cylindrical coordinate system
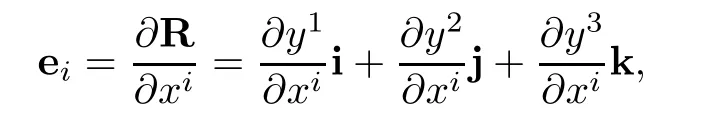
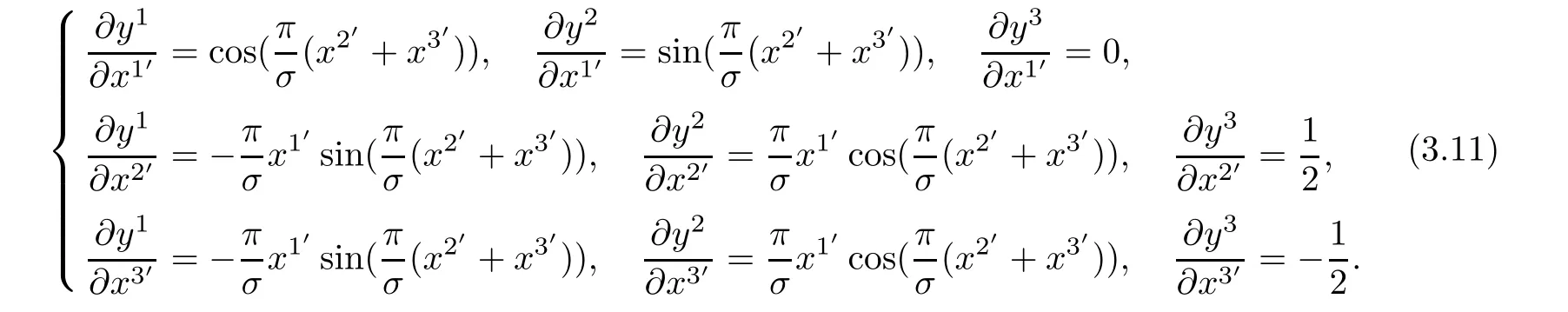
Therefore,bases of helical coordinate system and cylindrical coordinates system are respectively
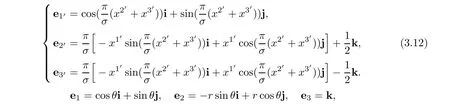
normalized basis
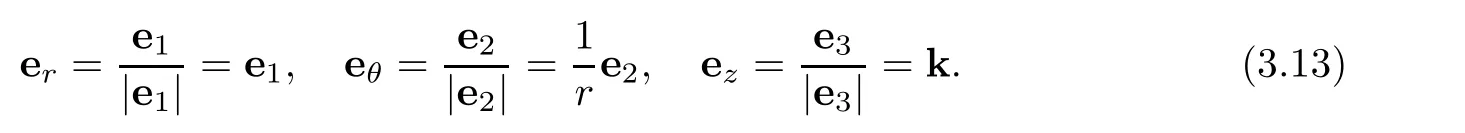
The metric tensors of Euclidean space ℜ3in helical coordinate system read

and in cylindrical coordinate system,

where
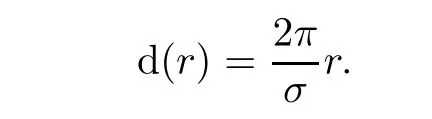
Because contravariant components gi′j′,gijof metric tensors satisfy
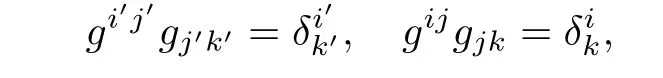
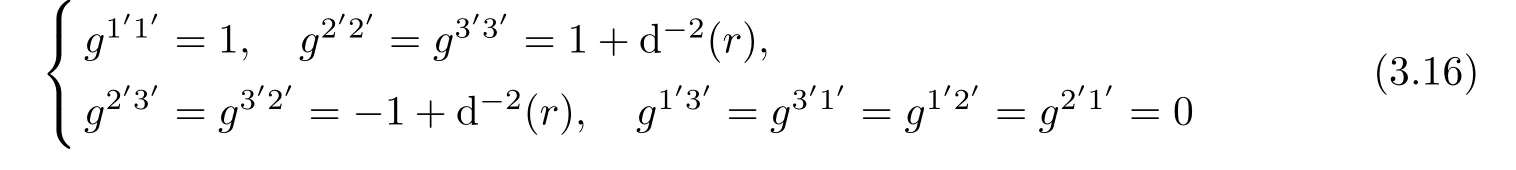
and
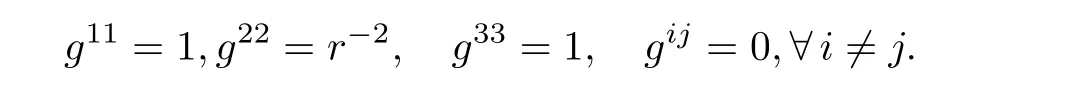
Remark 3.2It is well known that according to the regularity properties of tensor transformation as coordinate system occur transformation,we claim

Simple calculations using(1.1)show that

which coincides with(3.10).
4 Covariant Derivatives of Laplace-Beltrami Operator and Trace Laplace Operator in Helical Coordinates
In engineering,one would like to find physical components of velocity in cylindrical coordinates system
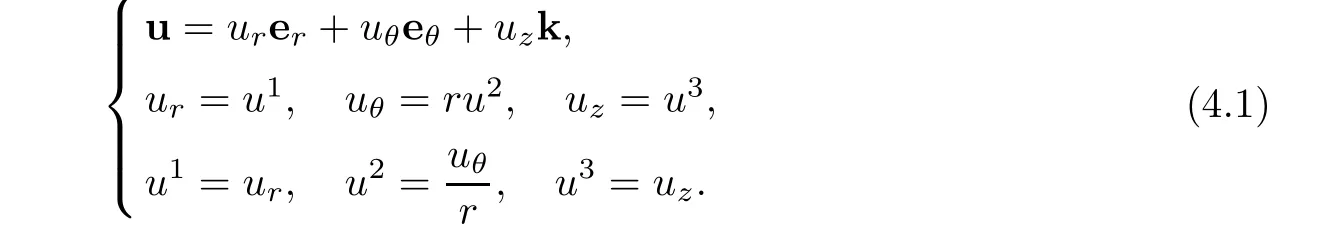
It is well known that velocity module is given by

According to transformation regular of 1-order tensor under coordinate transformation(see[8]),it infers the relations between contravariant components of velocity in helical coordinates and physical components in cylindrical coordinate
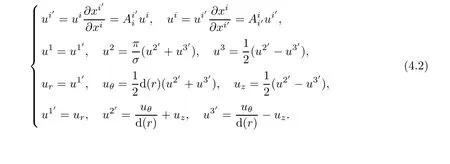
It is clear that if contravarinat components ui′of velocity of the fluid in helical coordinates system are found,then corresponding physical component(ur,uθ,uz)in cylindrical coordinates can be obtained by(4.2).
Throughout this article,Greek in dices and exponents belong to the set{1,2}while Latin in dices and exponents(expect when otherwise indicated,as when they are used to index sequences)belong to the set{1,2,3},and Einstein summation convention with respect to repeated in dices and exponents is systematically used.
Next we consider Christoffel symbolof second type in helical coordinates.It is well known[8]that second type Christoffel symbol in cylindrical coordinates are
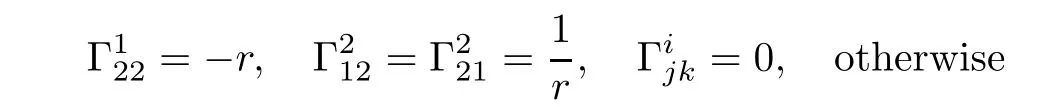
where
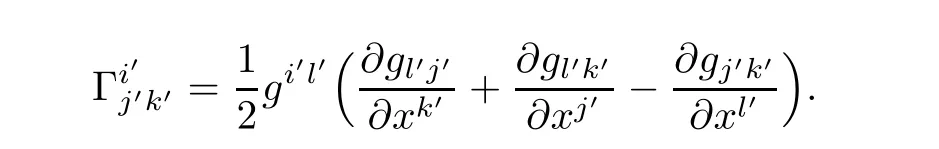
We claim,by simple calculation using(3.10)and(3.12),that
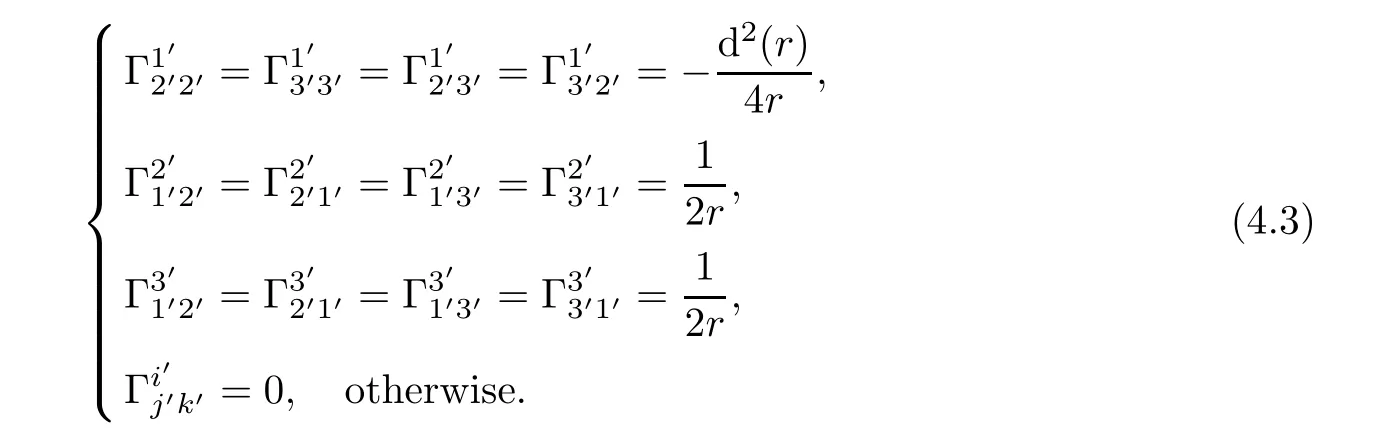
4.1 Covariant derivatives of the velocity in helical coordinate system
Proposition 4.1The covariant derivatives of contravariant components of the velocity in helical coordinate are
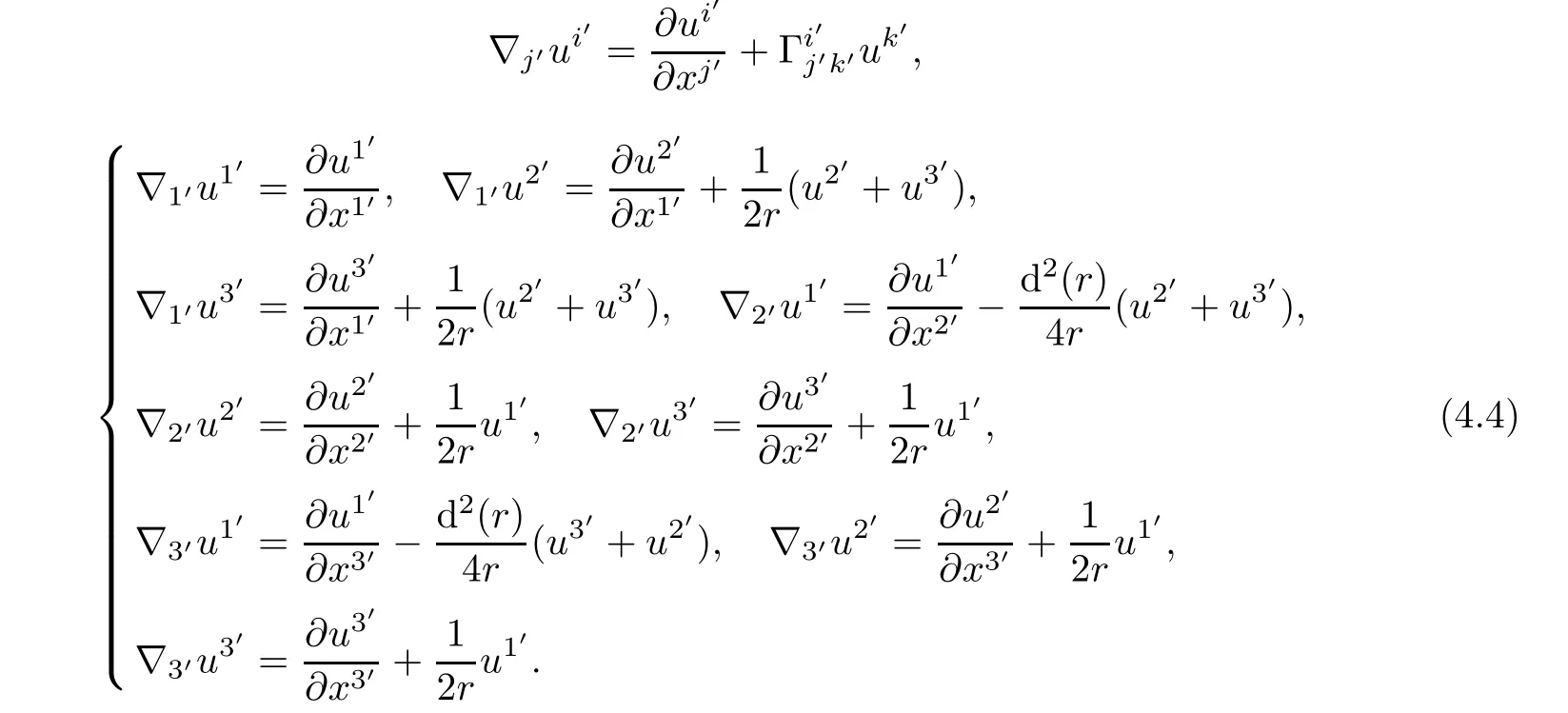
The divergence of the velocity in helical coordinates is
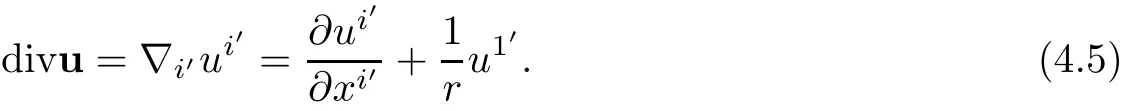
ProofIt is easy to derive(4.4)and(4.5)from(4.2).
Proposition 4.2The Laplace-Beltrami Operator for the scale field and the trace-Laplace operator for the tensor of first order(vector field)are given,respectively,by
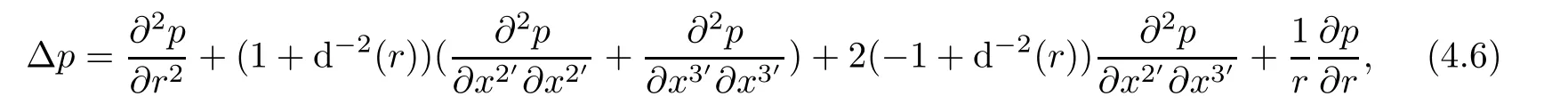
and
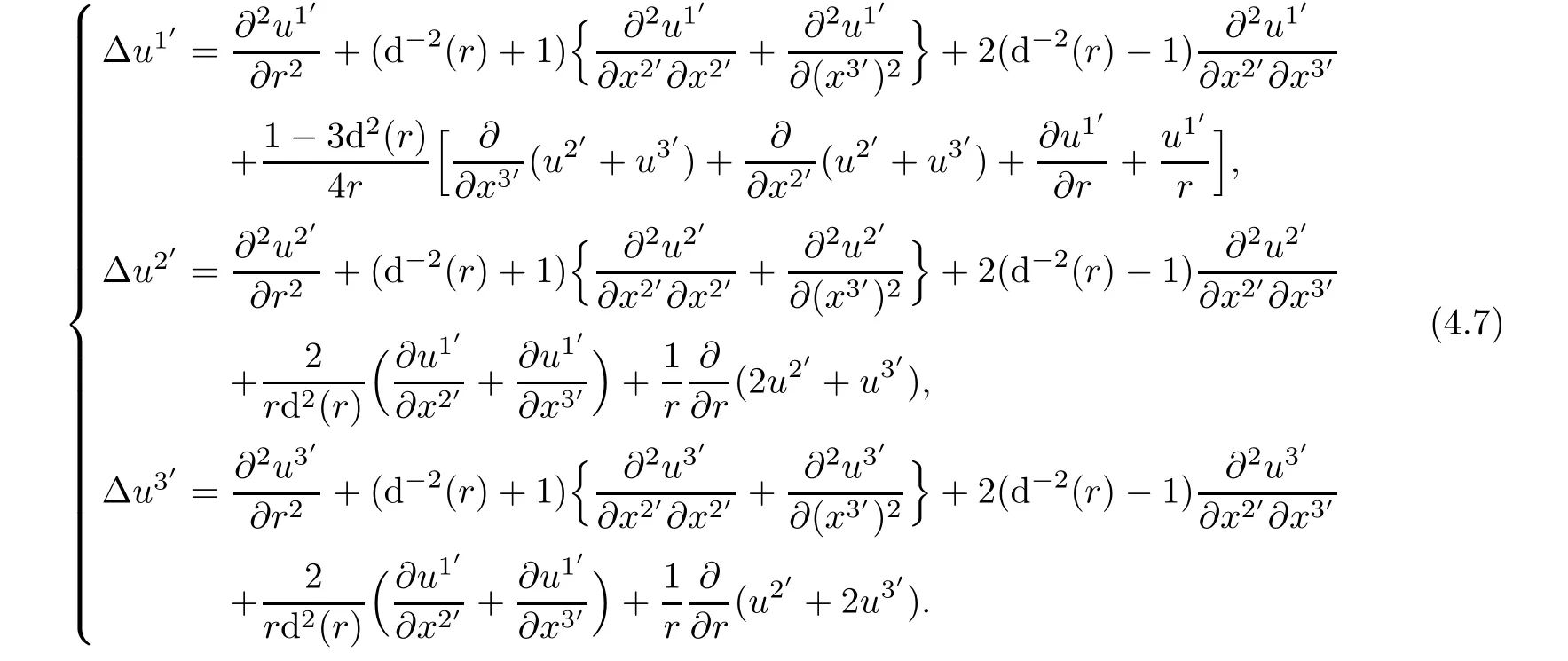
which can also be expressed in terms of physical components in cylindrical coordinate

Remark 4.3The followings is more useful
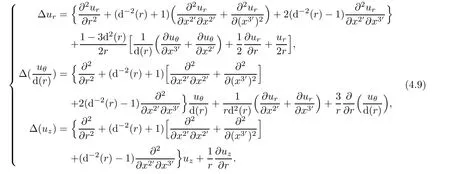
ProofIndeed,we have
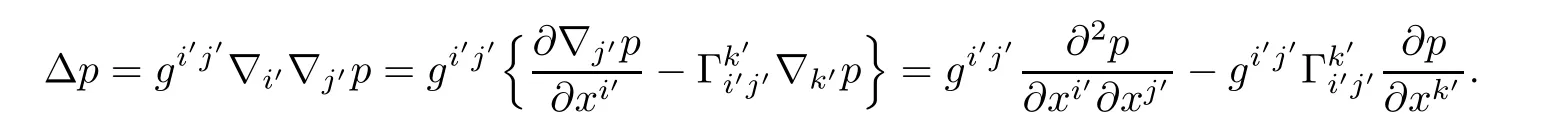
Owing to(3.12)and(4.2),it yields
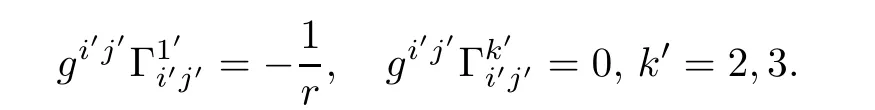
Combining the above formulae with(3.16)yields(4.7)
On the other hand,trace-Laplace operator act on velocity vector
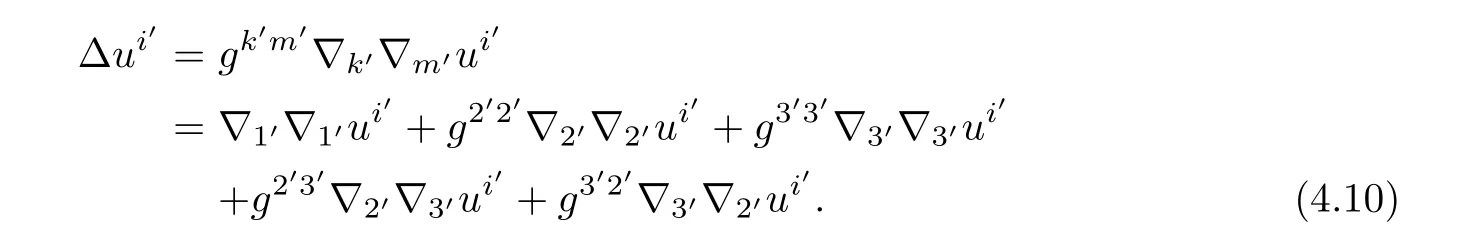
In details,we obtain
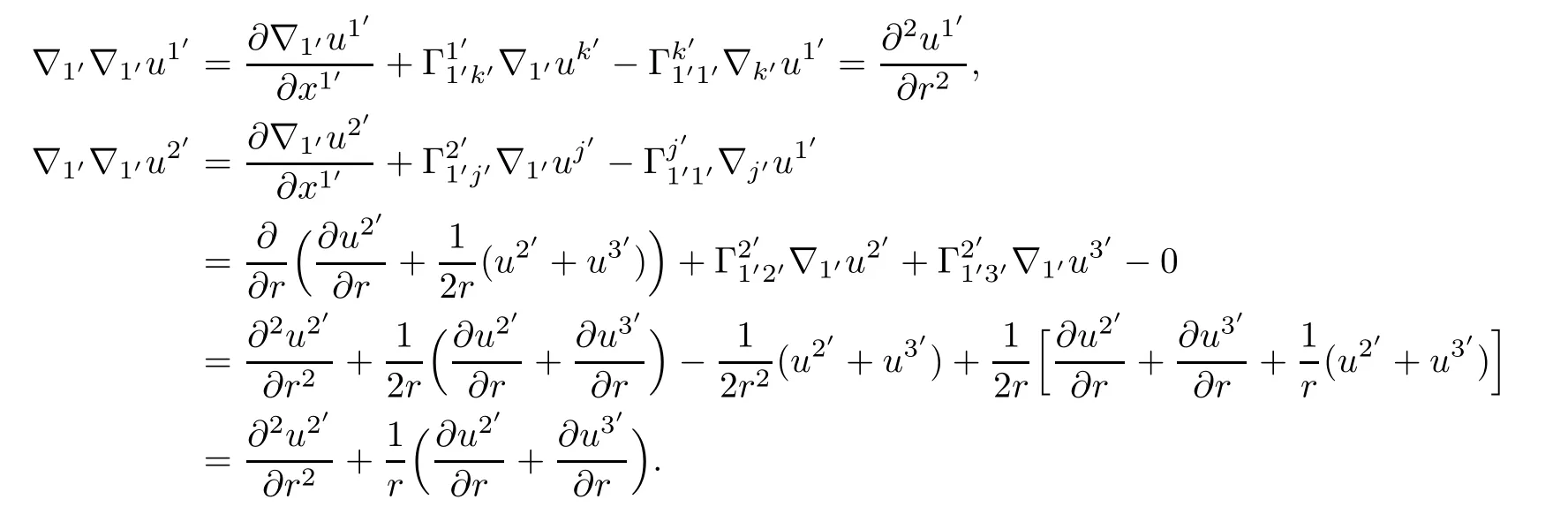
In a similar manner,we obtain the following formulae:

Accoding to Riesz formula in tensor analysis([8]),we have
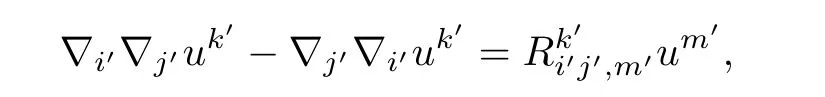
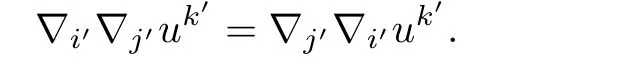
To sum up,it is easy to derive(4.8).Taking into account(4.2),it yields(4.9).Moreover,letting(4.82)±(4.83),using(4.2)we obtain(4.10).Thus,the proof is complete. ?
Proposition 4.4Relative acceleration velocity and Coriolis acceleration in Helical Coordinates are given by
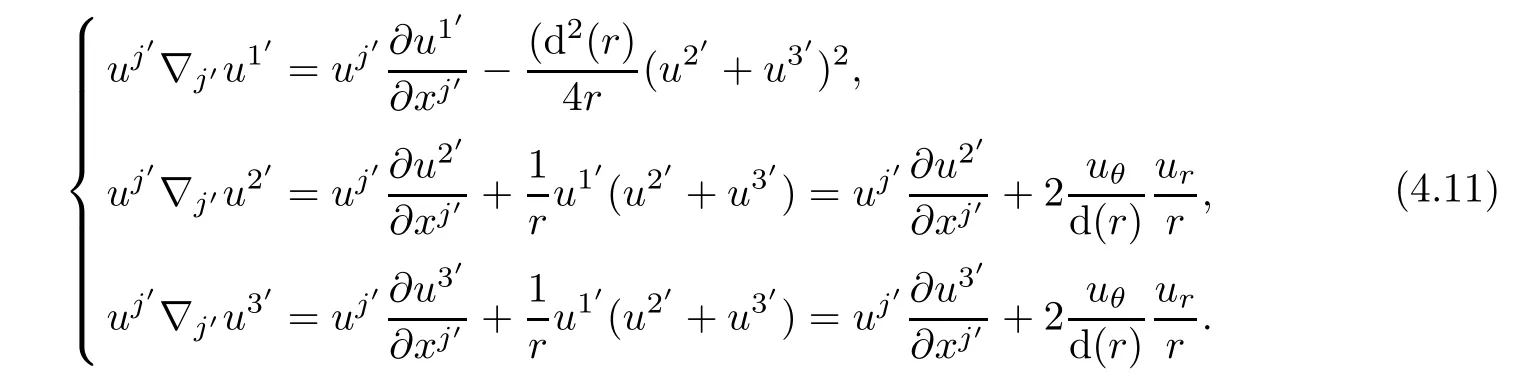
In terms of physical components,we have
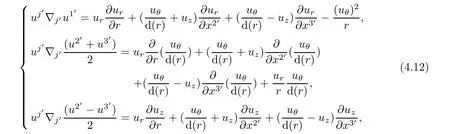
while contravariant components of Coriolis acceleration 2~ω×u in helical coordinated are

ProofUsing(4.4)and(3.14)(3.16),simple calculations show(4.11)and(4.12).
Next,we consider Coriolis acceleration in helical coordinates.Assume that the coordinate are rotating along z-axes with angular vector~ω.The Coriolis acceleration is 2~ω×u,reading it in helical coordinate
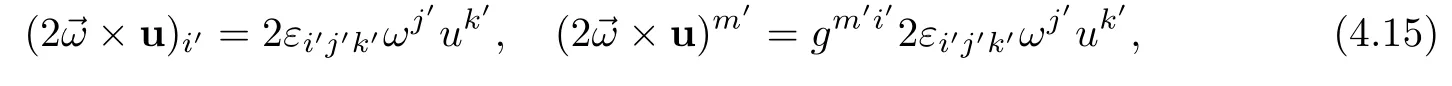
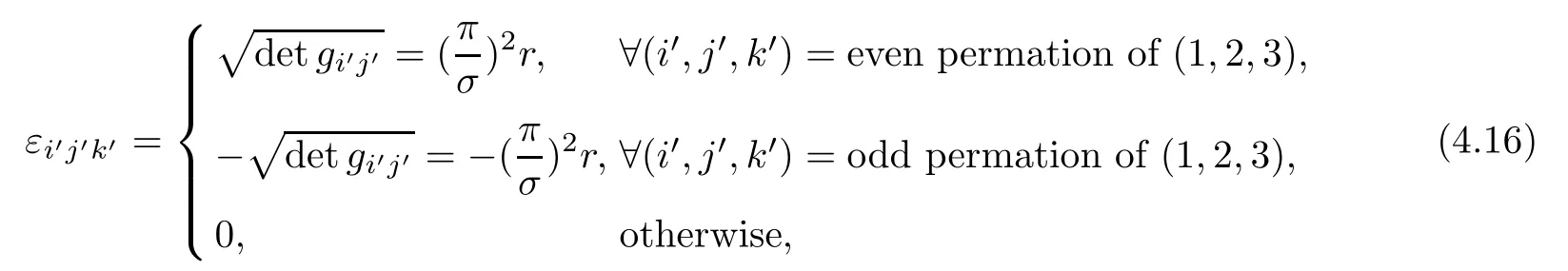
by virtue of(4.15),(4.16)and(3.14),(3.16),it yields(4.13)and(4.14).Thus,the proof is complete. ?
In addition,we give the following formulae for gradient,divergence,and vorticity operators in helical coordinates

Vorticity in Helical Coordinate System is given by covariant form
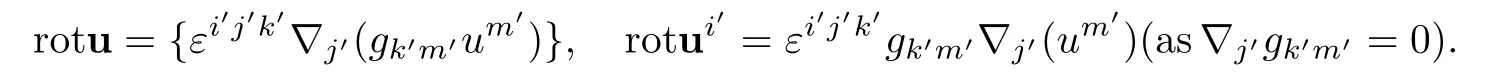
Using(3.10)and(4.4),simple calculation show that

Similarly,we have
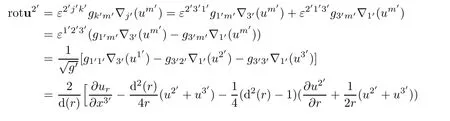

Hence,we obtain
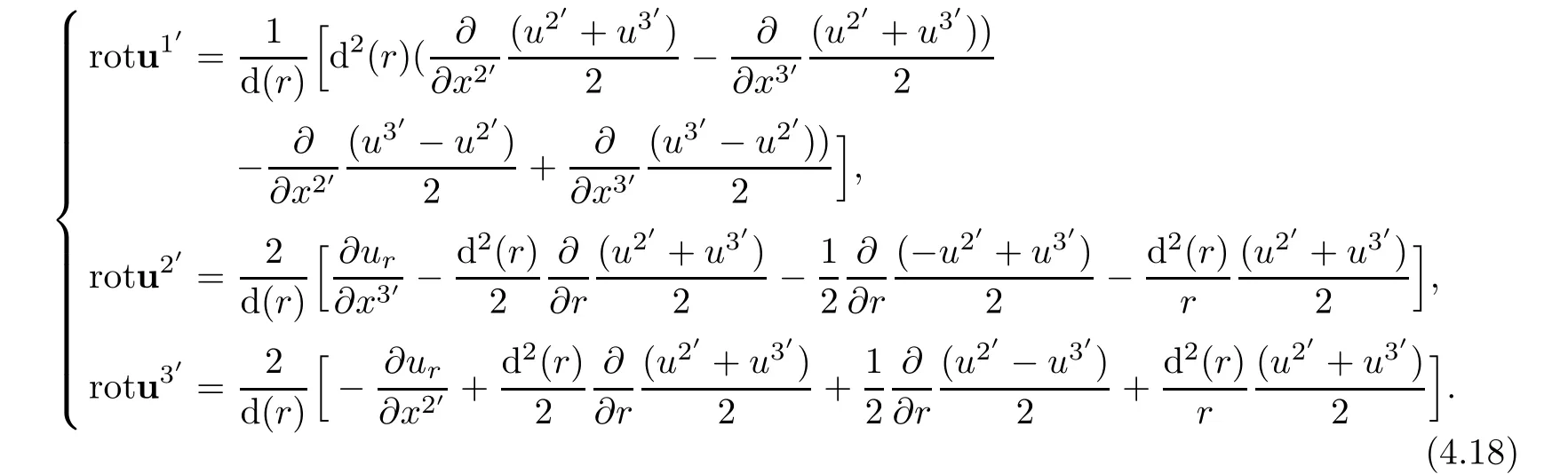
Expressing it in terms of(ur,uθ,uz)and noting,we assert that

In terms of physical components in cylindrical coordinate,rotation of the velocity shows
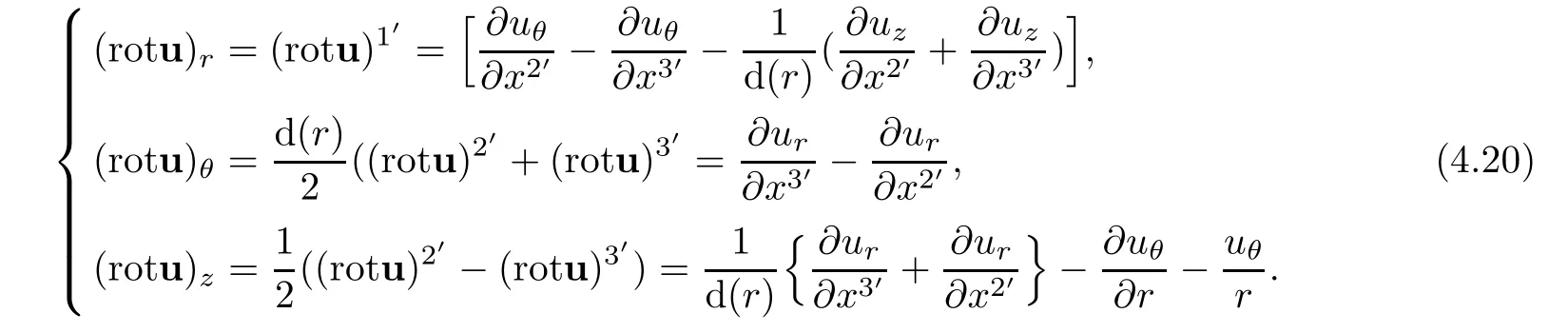
For the helical velocity,that is,using stream functions
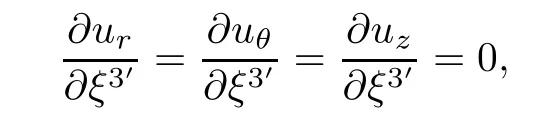
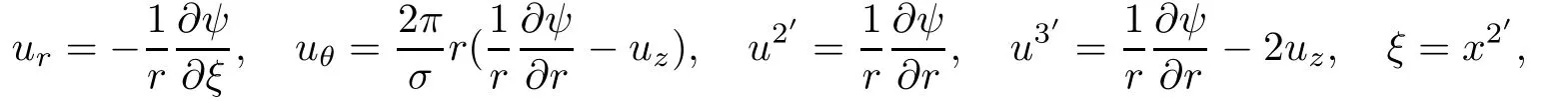
then,we obtain
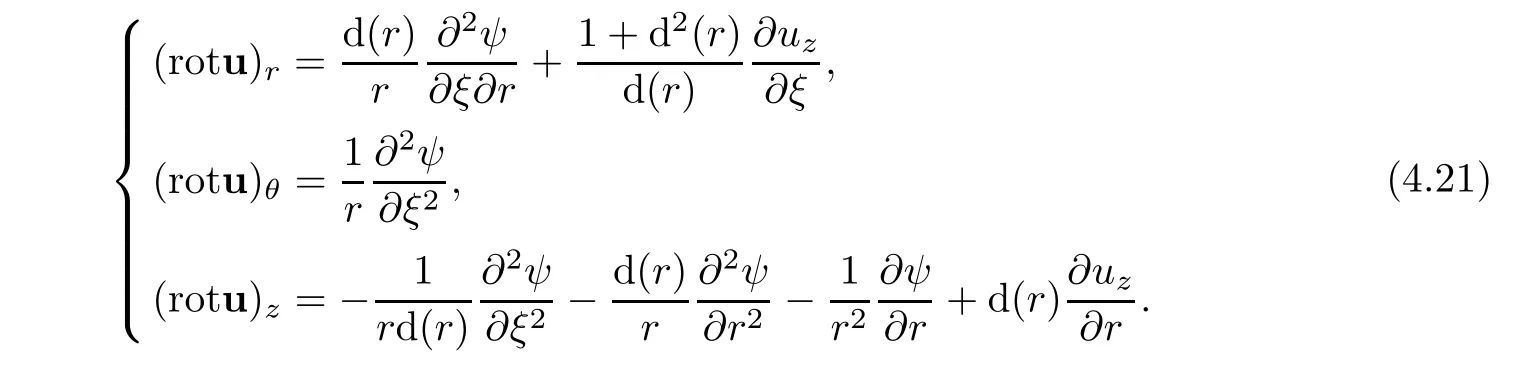
5 NSE in Helical Coordinate Systems
We consider the Navier-Stokes equations in a domain Ω between ΣHand in finite cylindrical surface r=r1with periodic step σ >0.LetIn helical coordinate,letmap intois clear that(3.1)shows that

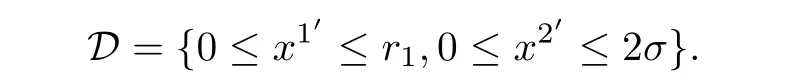
Then,set 2D-3C(two-dimensional,3 components)Sobolev space as
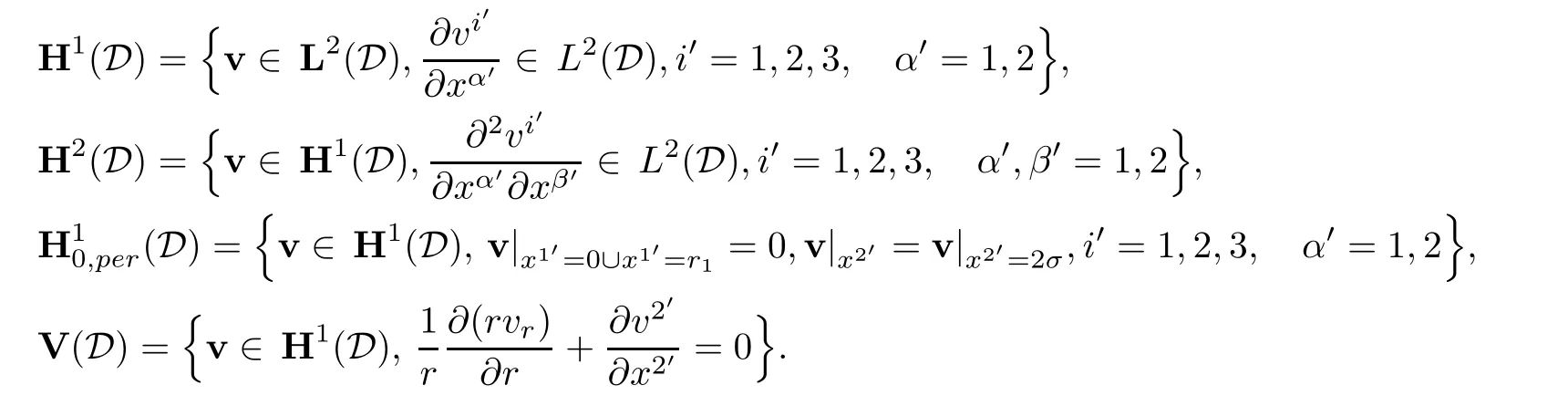
In what follows,Latin indices and exponents:(i,j,k·)take their values in the set{1,2,3},while Greek indices and exponents(α,β,γ,···)take their values in the set{1,2}.In addition,Einstein’s summation convention with respect to repeated indices and exponents is used.
We can therefore state the initial boundary value problem for the rotating Navier-Stokes equations in the fundamental domain

Proposition 5.1In helical coordinate system,Navier-Stokes Equations read

which can be expressed in terms of physical components(ur,uθ,uz)of velocity in cylindrical coordinate
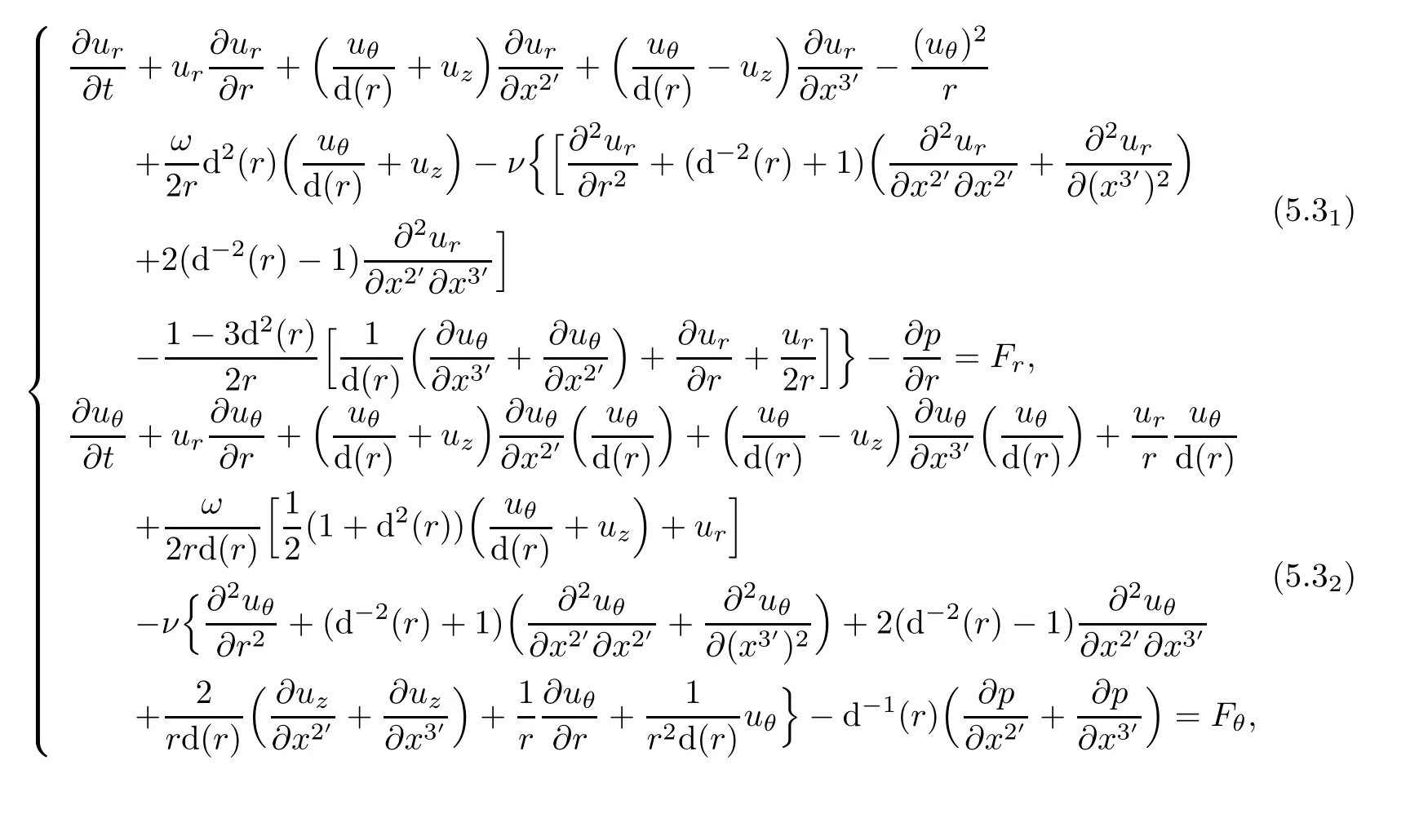
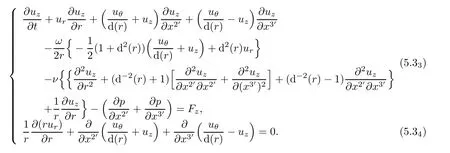
ProofLet us write(5.1)in covariant invariant form

Taking into account Proposition 3.1,we find
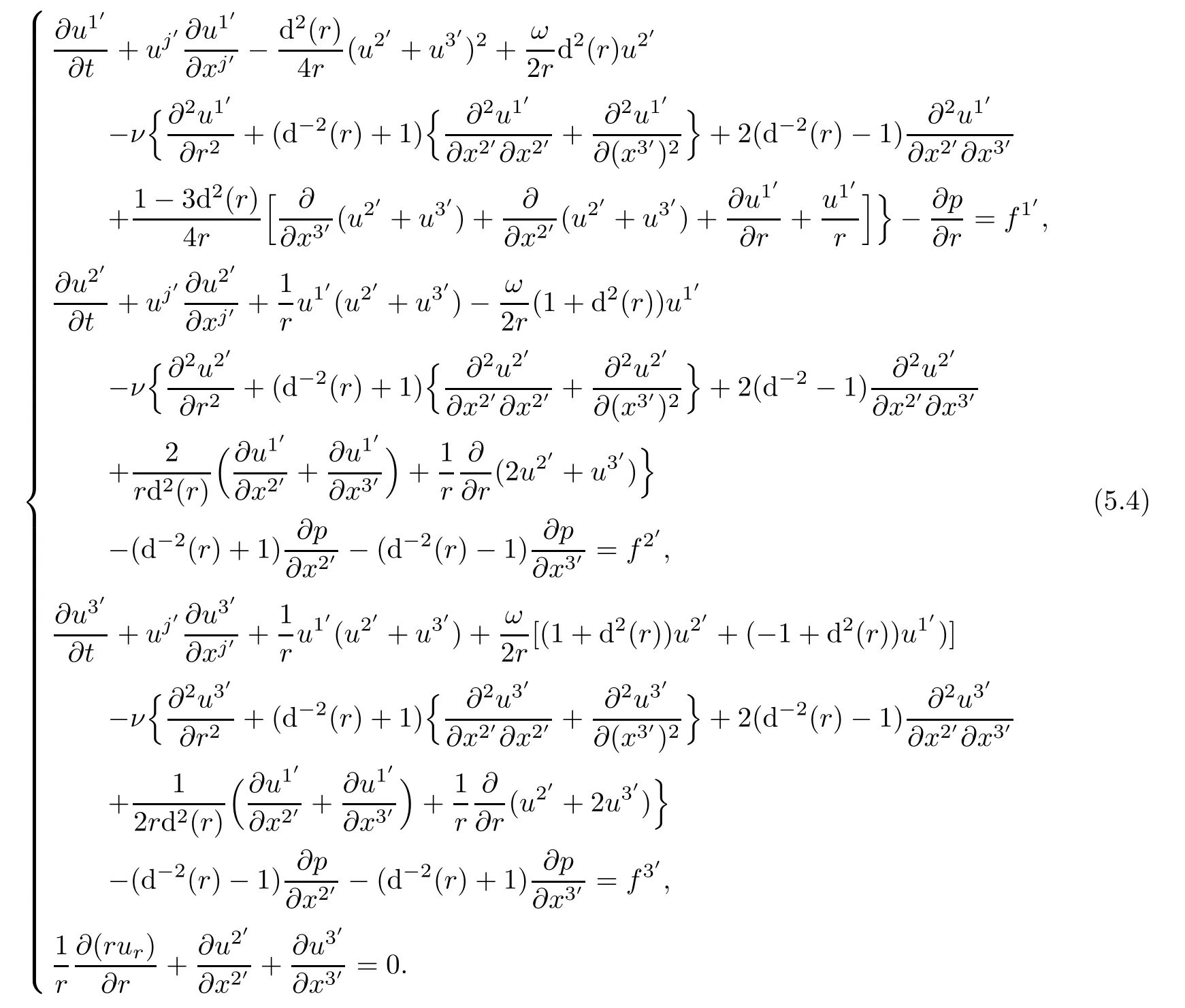
It is obvious that(5.4)is(5.2).To prove(5.3),note
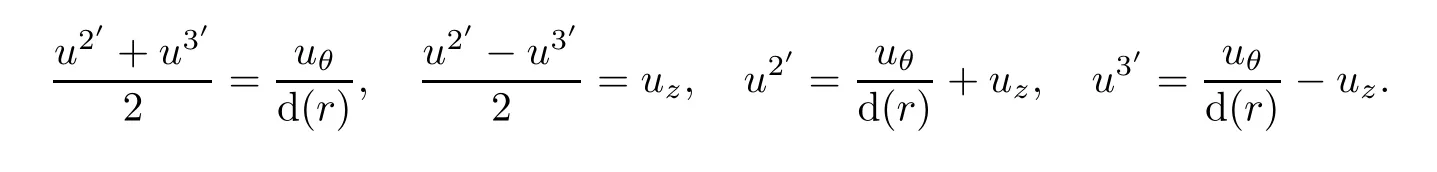
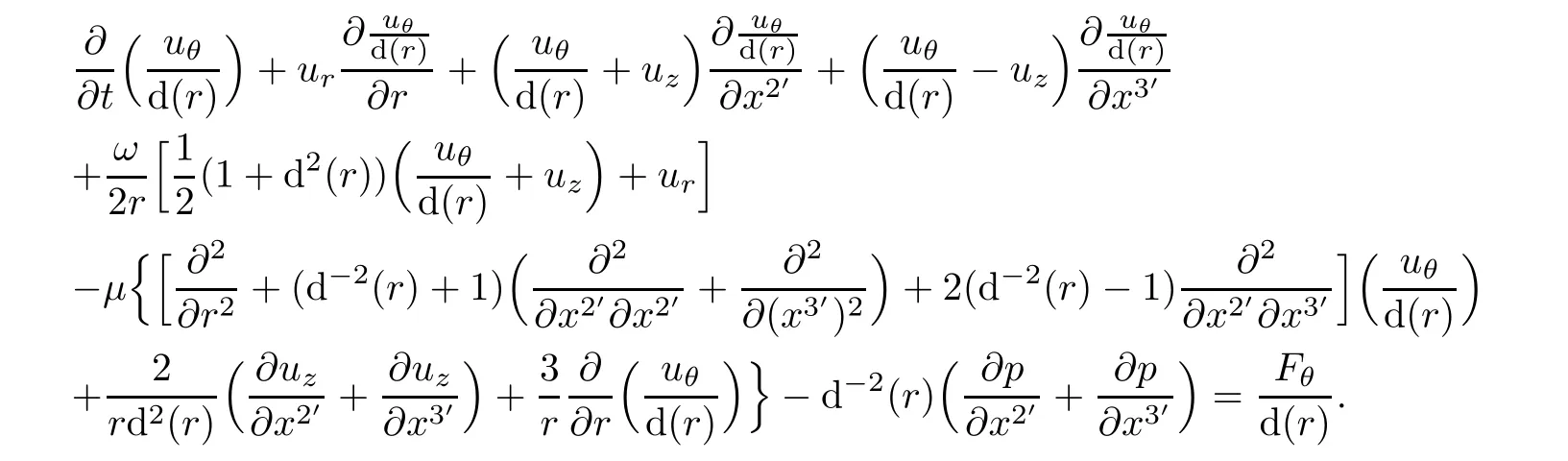
This is(5.32).In a similar manner,making subtractleads to(5.33)directly.Thus,this ends our proof.
6 Helical Symmetric Solution of Navier-Stokes Equations
Helical symmetry is invariance under a one-dimensional group of rigid motions generated by a simultaneous rotation around a fixed axis and translation along the same axis.The key parameter in helical symmetry is the step or pitch σ,the magnitude of the translation after rotating one full turn around the symmetry axis.
In Cartesian coordinates(y1,y2,y3),the action of helical group of transformation Gσonℜ3is defined by

that is,a superposition of a simultaneous rotation around the y3axis with translation along the y3.Gσis uniquely determined by σ,which is called the step,or pitch.Invariant curves for the action of the helical group Gσare helices having the y3axis as axis of symmetry.The cylinderis an invariant set for the action of Gσfor all σ.A change of the sign in σ corresponds to switching the orientation of the helices preserved by the group action from right-handed to left-handed.Without loss of generality,we will restrict our attention to the case of σ>0.
Taking(3.1)into account,in the helical coordinates(xi′,i=1,2,3),the action of helical group of transformations Gσsubstituting(3.1)into(6.1)becomes

because of

It is well known that after transformation of the coordinate,a velocity vector u’of the fluid areaccording to the rule of transformation of the tensor under transformation of coordinates.Hence,we concludefrom(6.2)
Lemma 6.1A solution{u,p}of Navier-Stokes equations is a helical symmetric solution,if and only if which is independent of x3′in helical coordinate,that is,
Proposition 6.2The helical symmetric solutions(u,p)for NSE satisfy the following formulae:
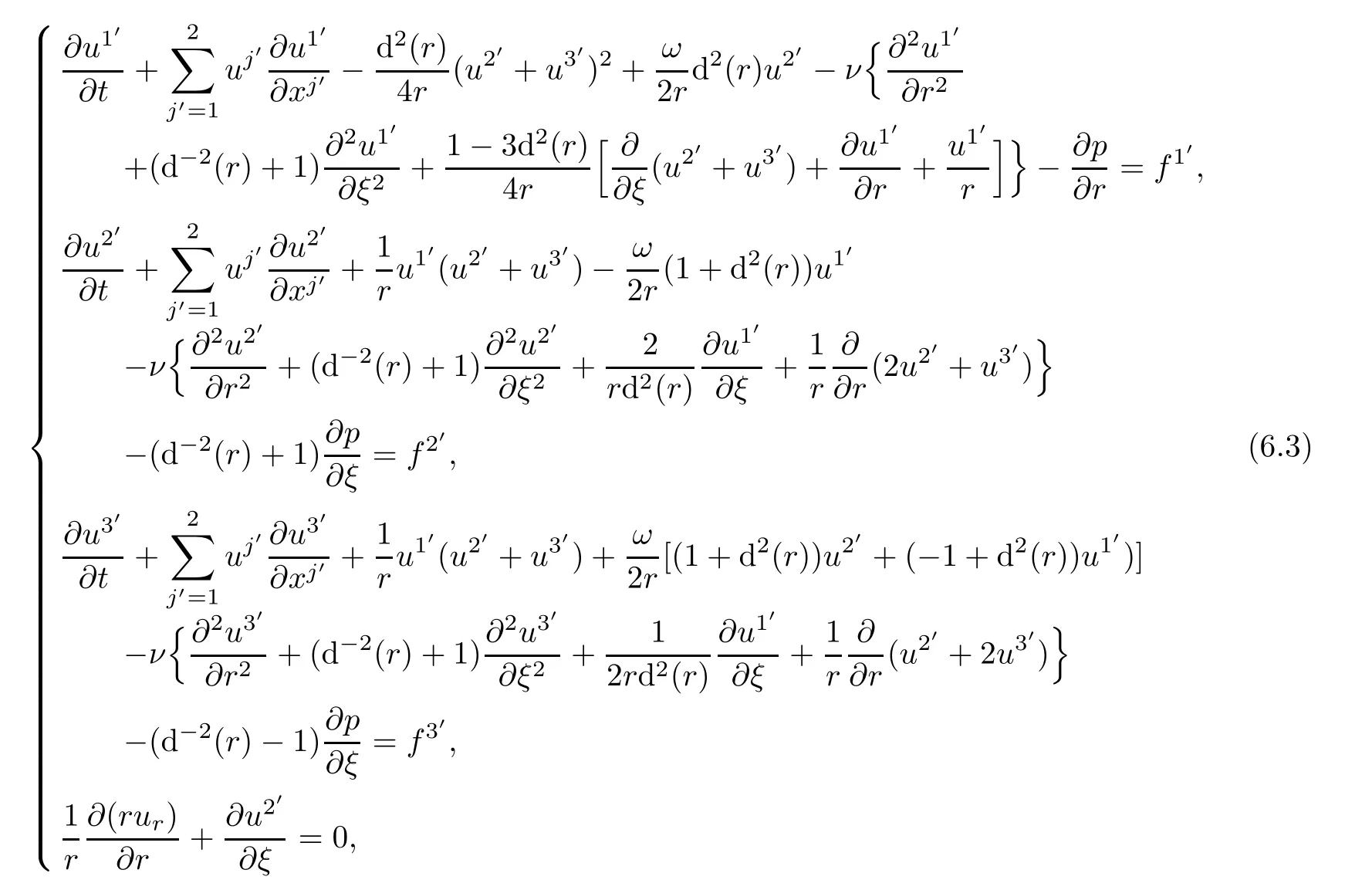
which can be expressed in terms of physical components(ur,uθ,uz)of velocity in cylindrical coordinate
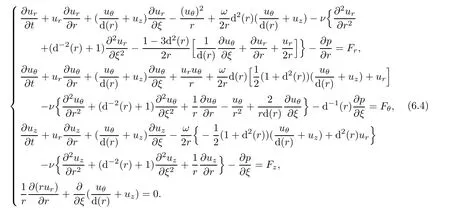
ProofIndeed,we have
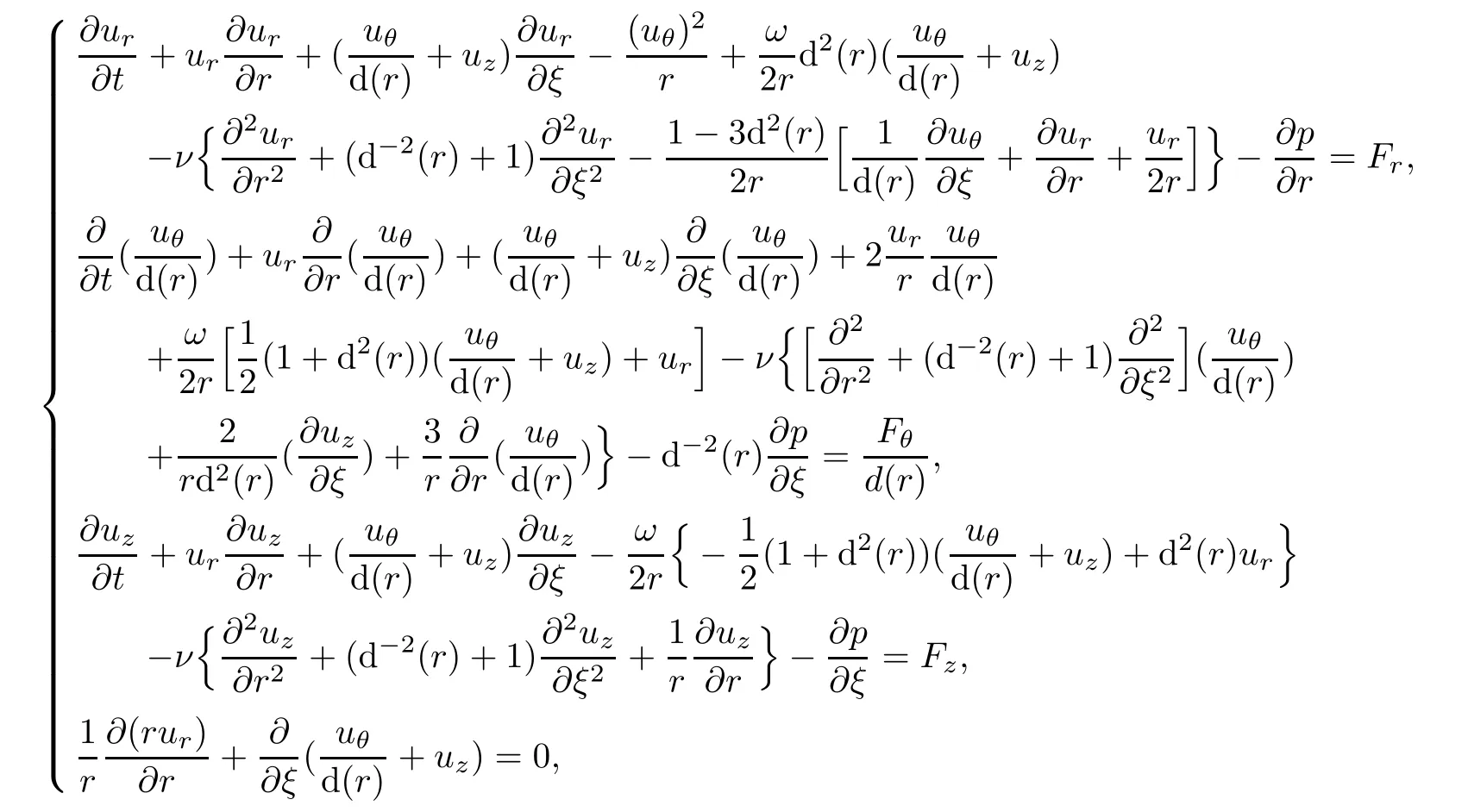
where ξ=x2′.By
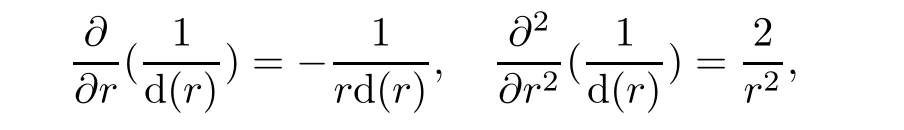
therefore
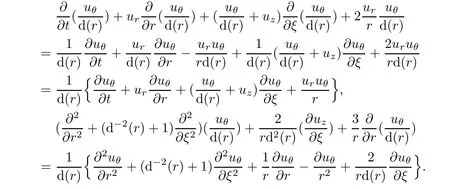
Hence,the above second equations becomes

Coming back,it yields(6.4).Thus,the proof is complete.
It is clear that(6.34)or(6.43)allow us to define stream function ψ as
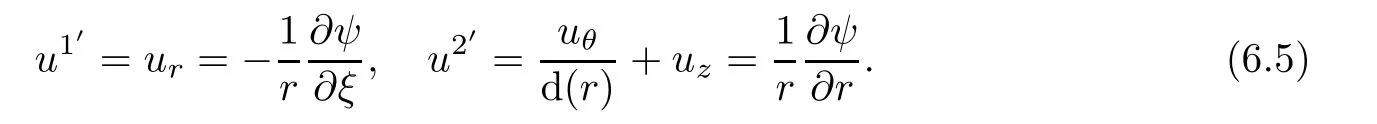
Of course,(6.34)and(6.44)are trivial,
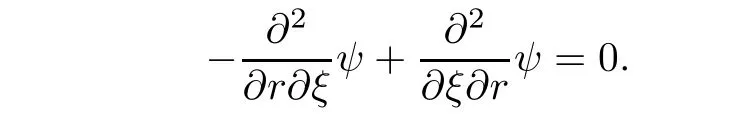
In order to eliminate the terms containing pressure,makingleads to

Substituting(6.5)into(6.6),then calculations show that

On the other hand,making d(r)× (6.42)–(6.43),we claim
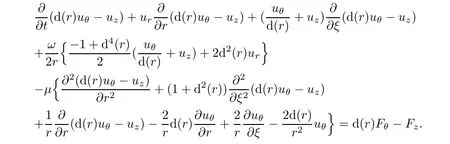
Because
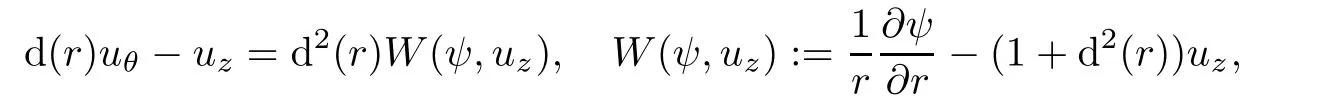
simple calculations show that
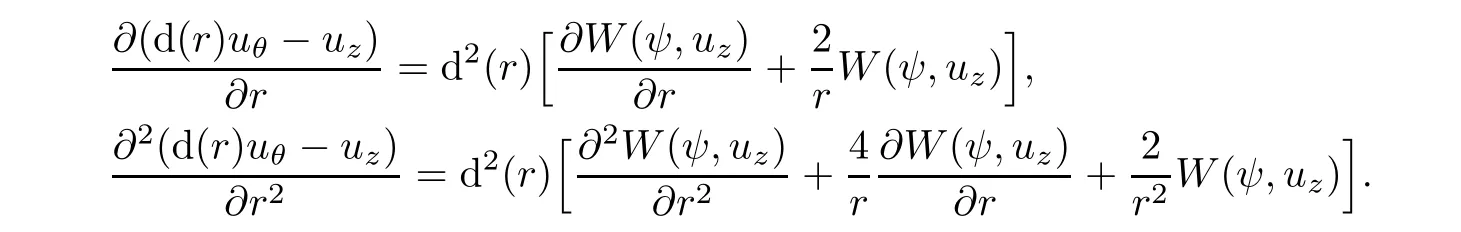
Taking the definition of stream function into account,we claim
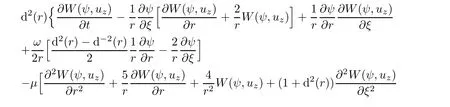
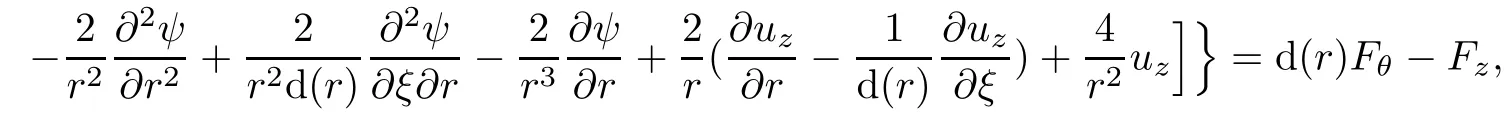
or
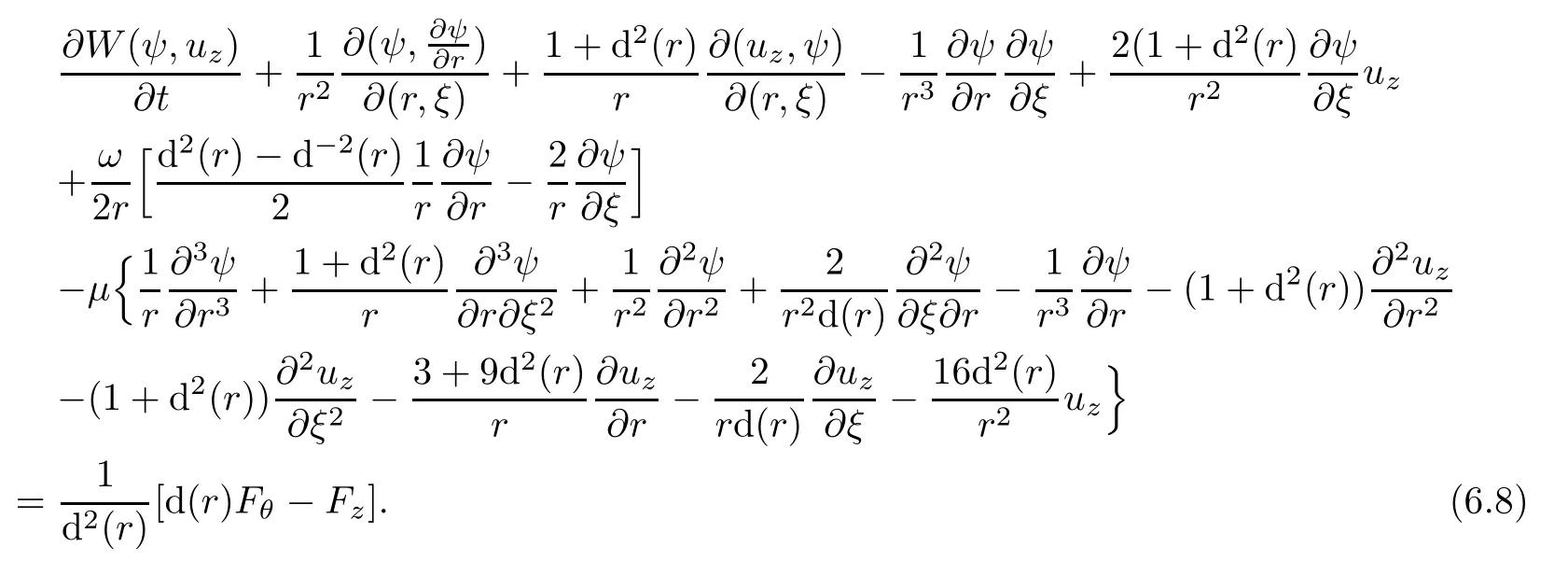
Finally,we conclude that the stream functions(ψ,uz)satisfy the following boundary value problem.
Proposition 6.3The stream functions(ψ,uz)for Navier-Stokes equation in domainin helical coordinate satisfy the following boundary value problem

It is clear that this is a 2D-3C(two dimensional problem with three components of the velocity vector field of the fluid)problem.
Associated steady state Stokes equations are given by
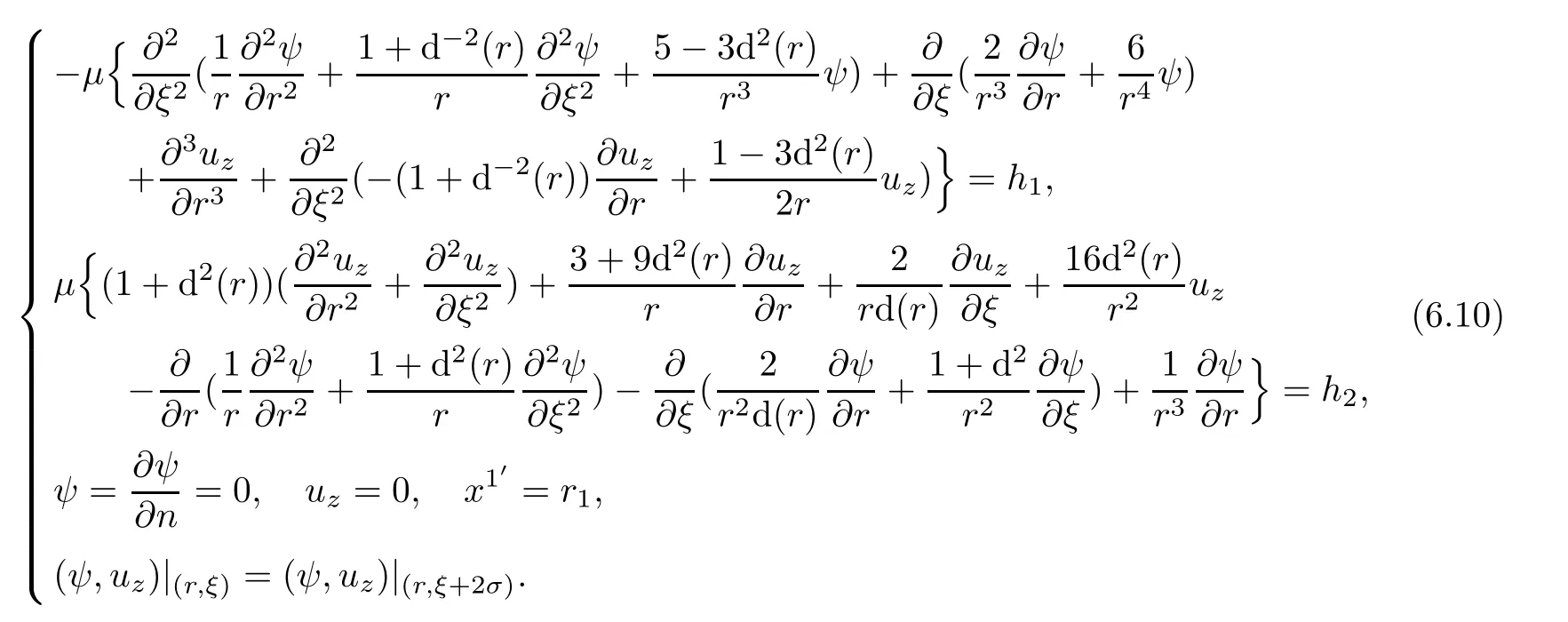
7 Variational Formulations
It is well known that invariant formulation for rotating Navier-Stokes equation(5.1)with boundary conditions and initial condition is given by

It is well known that the domain occupied by incompressible fluids in ℜ3is denoted by Ω,which is a gap between helicoid ΣHdefined by(2.1)and cylindrical surface


Let us introduce Sobolev spaces as follows:

Also,we set

Moreover,we set
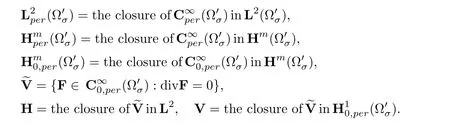
Note that divV is invariant form at any coordinate.We observe that

Then,we denote the inner product in H by

Because gi′j′is a positive definite matrix,the associated norm byis easy to show that the classical Poincare inequality also valid:the inner product inis equivalent to the inner product
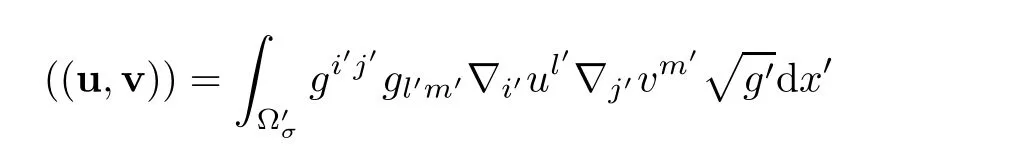
associated with the Dirichlet norm denoted by k·k.
Proposition 7.1Variational formulation associated with(7.1)is given by
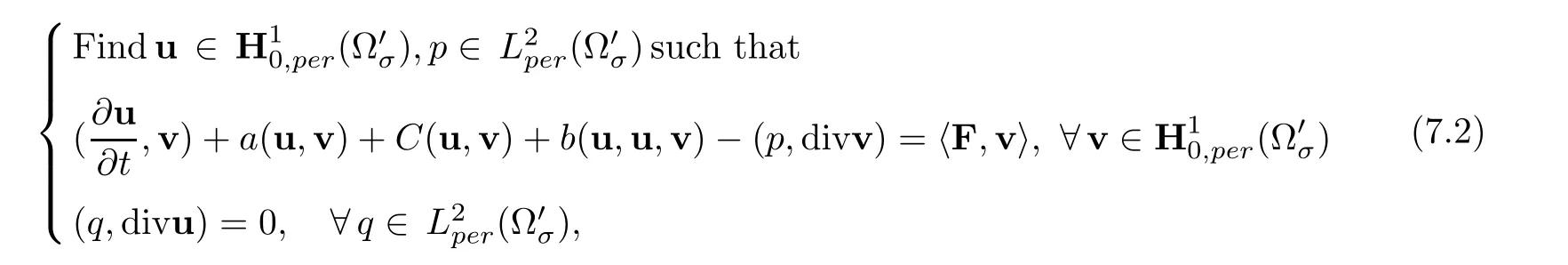
where in helical coordinates,trilinear forms and bilinear form are given by

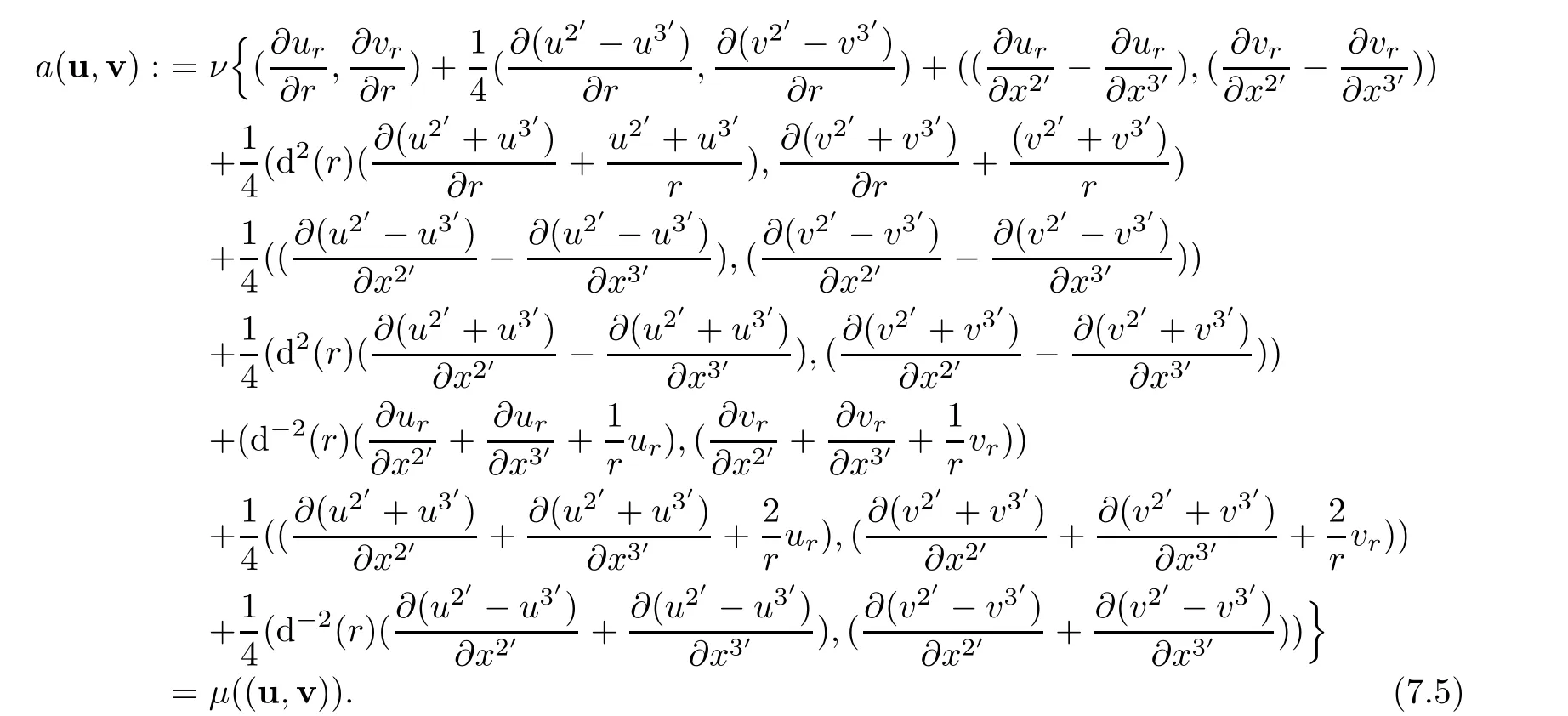
Each term also can be expressed in terms of physical components(ur,uθ,uz)of cylindrical coordinates for the velocity of the fluid,

ProofIndeed, firstly let us consider nonlinear term.By virtue of(3.14)and(4.4),in helical coordinate,we have
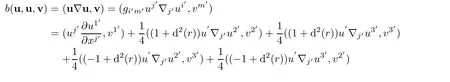

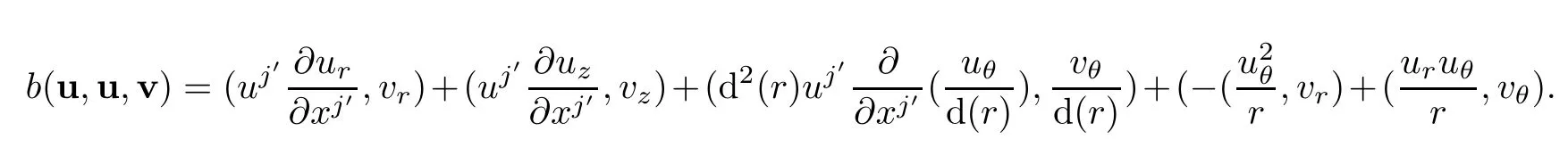
Because d(r)is independent of(x2′,x3′)andwe obtain
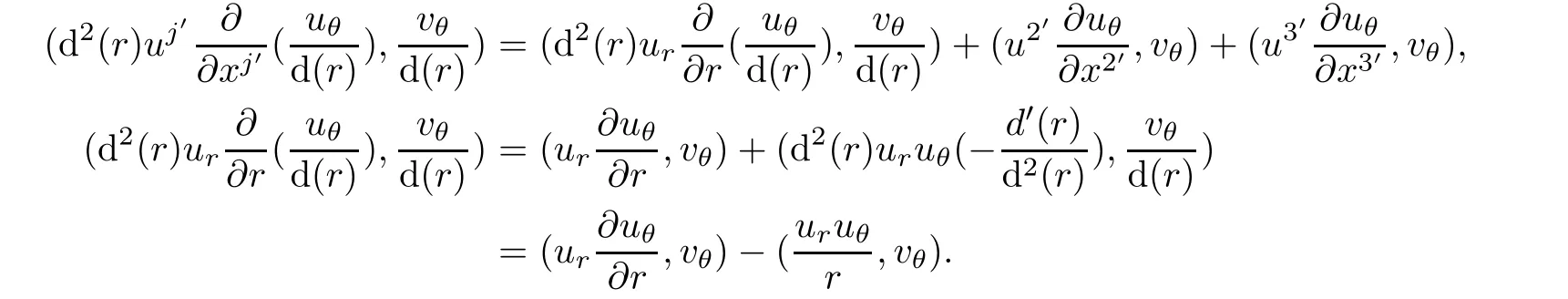
Hence,

To consider Coriolis force term,note that from(3.12),
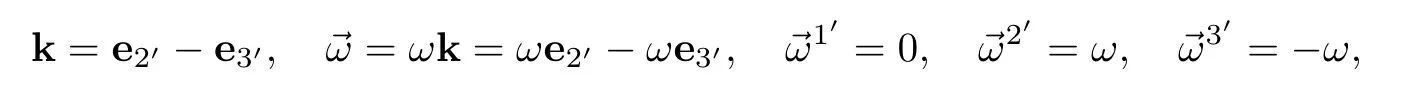
then we assert that
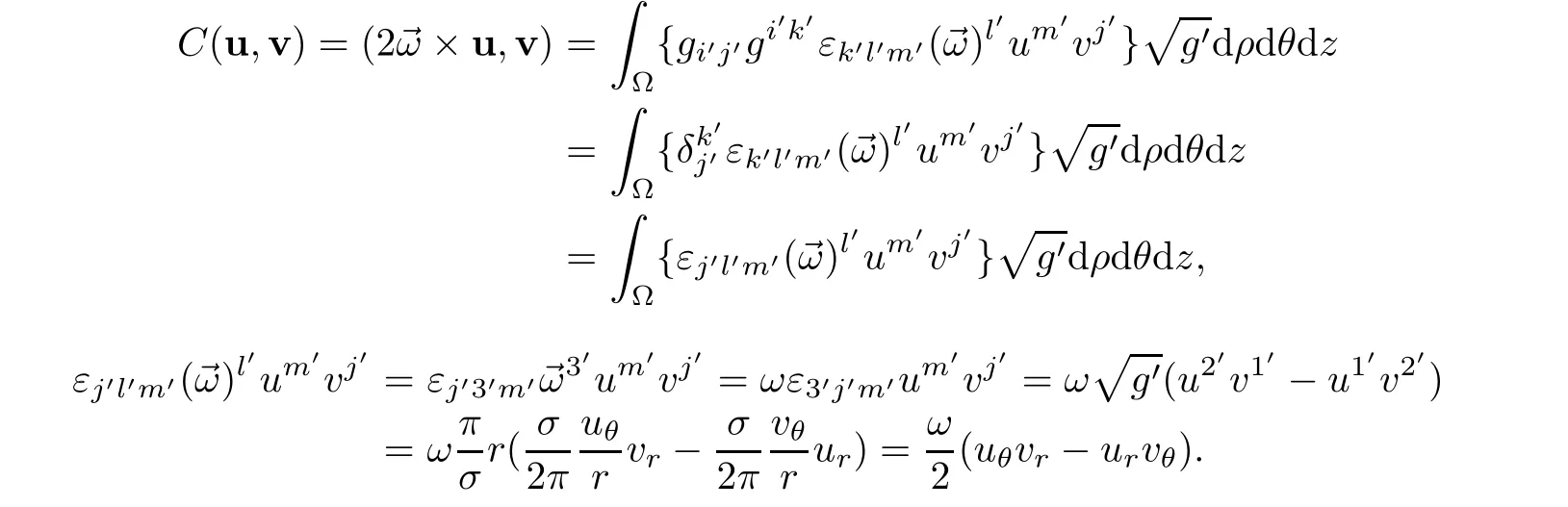
Hence,
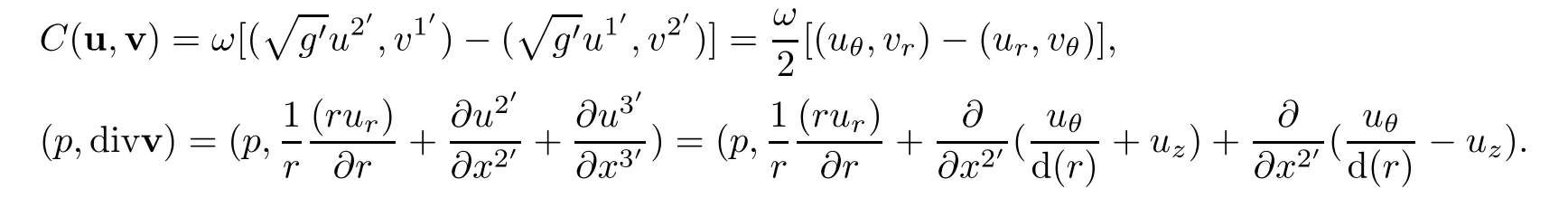
These are(7.7).In addition,we see that
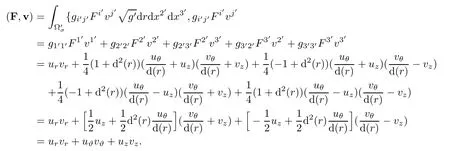
From this,it yields the second of(7.6).
Next,we consider bilinear form corresponding to dissipative term
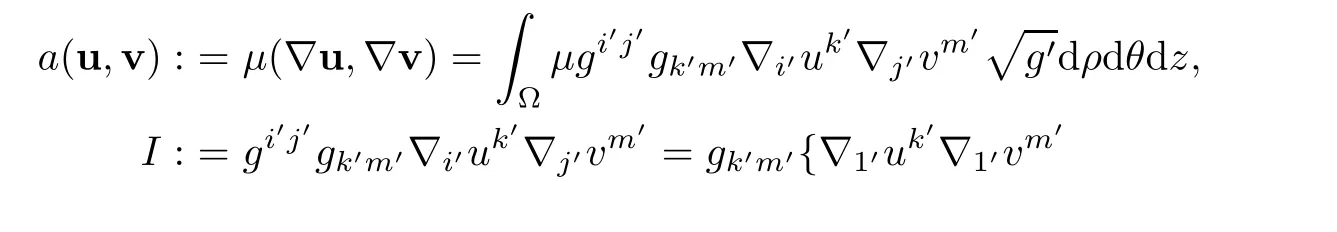
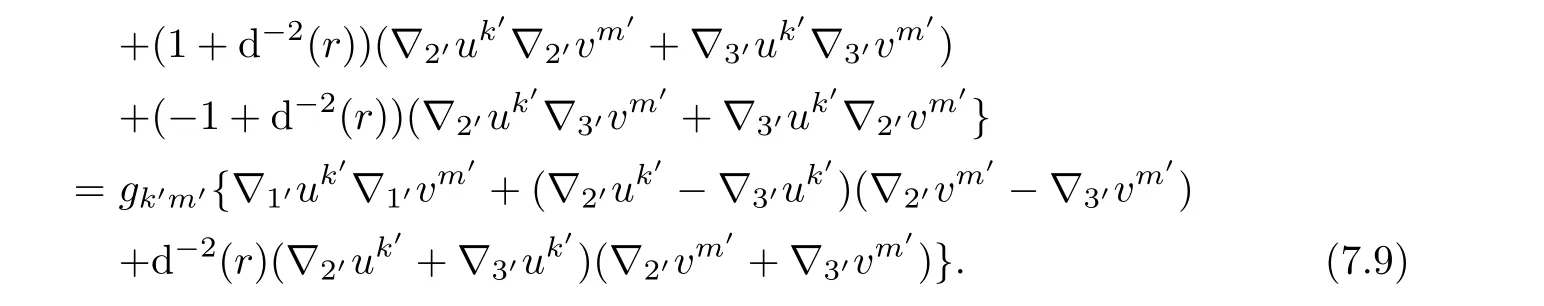
Because

finally,we have
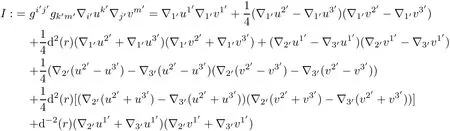
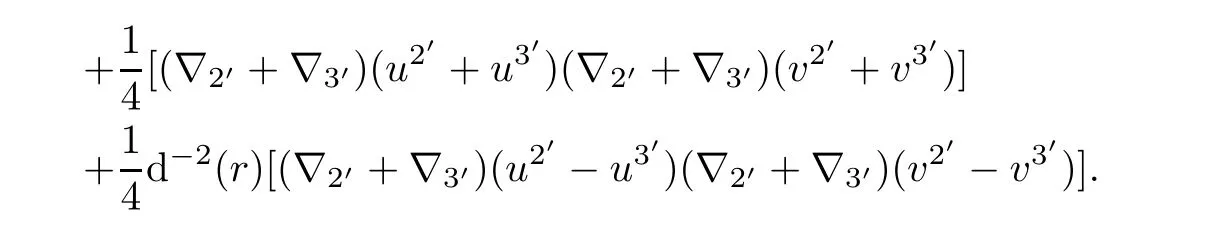
Applying(4.2),we obtain
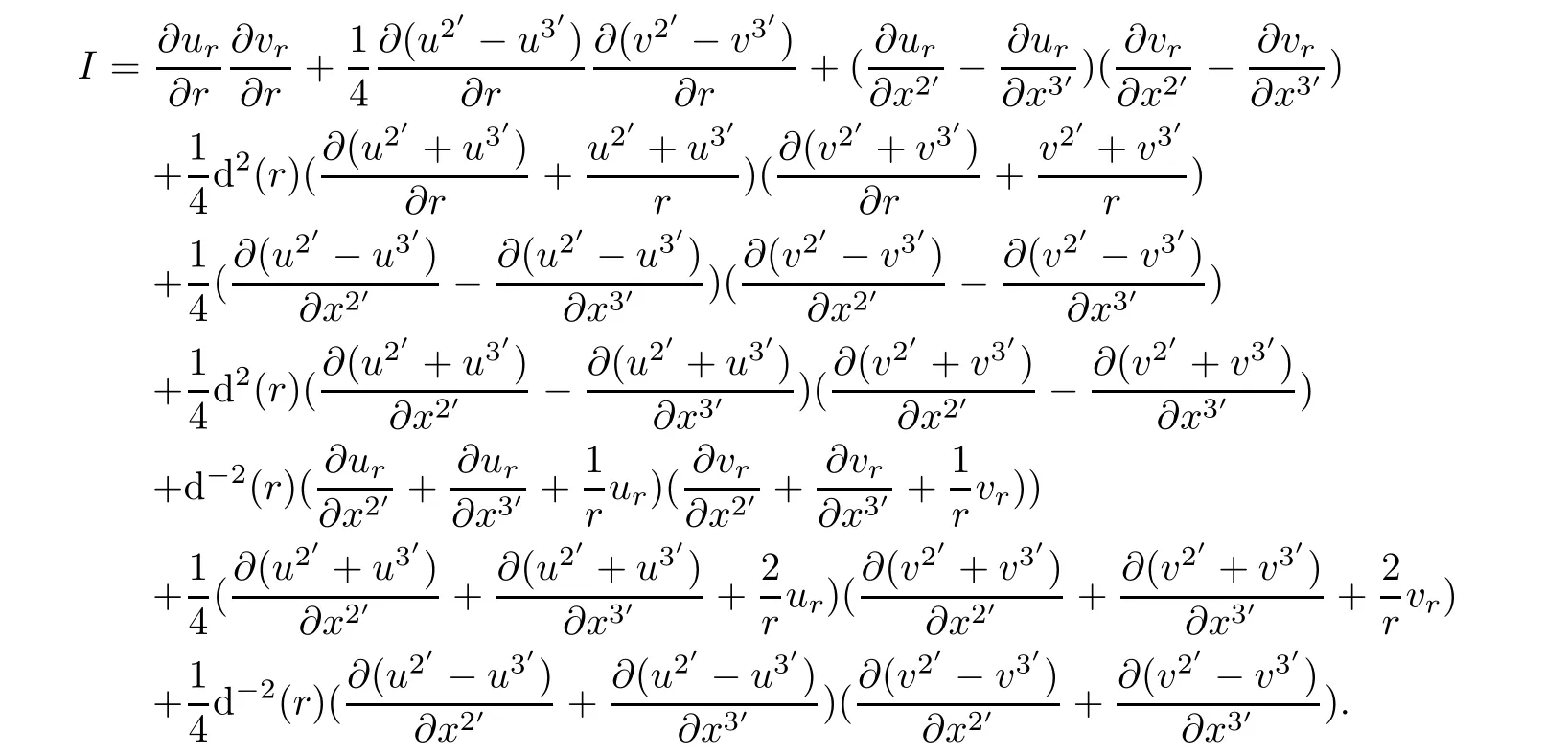
Using physical components of velocity in cylindrical coordinate
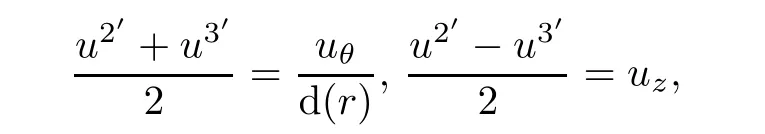
and taking the following equalities into account
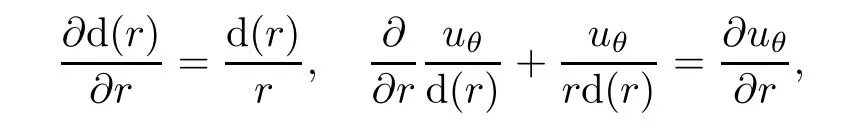
we obtain
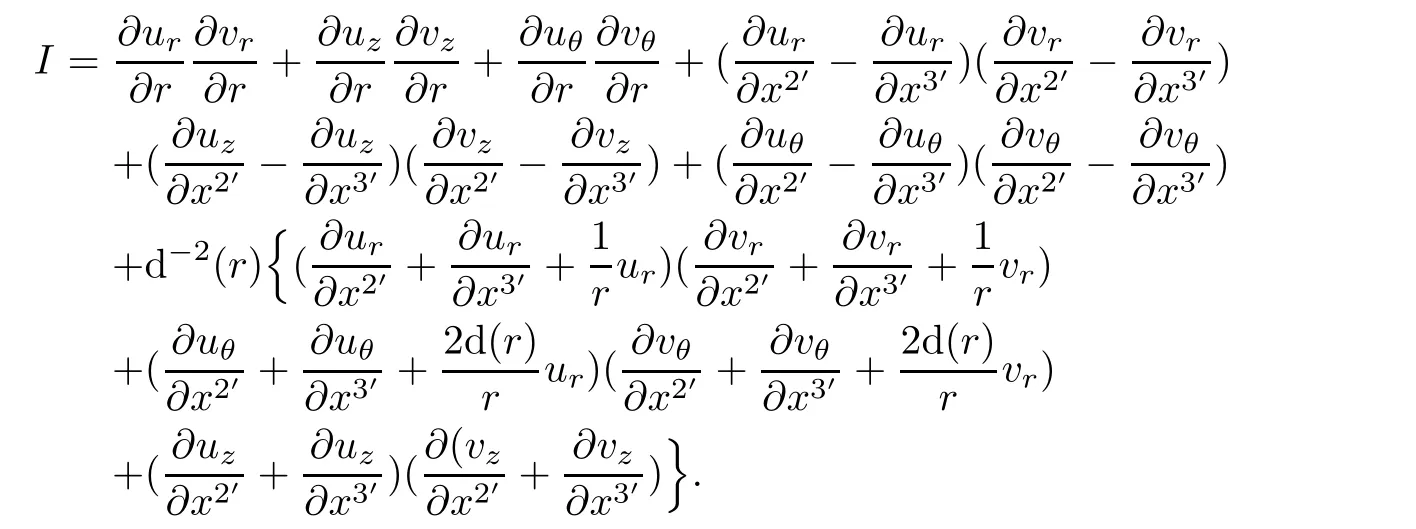
Substituting it into(7,9)leads to
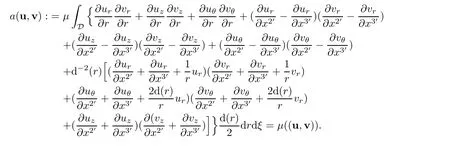
If u is a helical symmetric solution,then
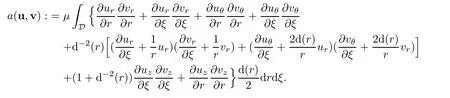
It infers(7.8).Similarly,it is not difficult to complete our proof for the proposition.
Variational formulation for helical symmetric solutions
In a similar manner as in Proposition 7.1,we assert
Proposition 7.2Variational formulation for the helical symmetric solution of NSE in helical coordinates is given by


By(5.34),we introduce the stream function defined by(6.5)and used unknown(ψ,uz).Then,from Proposition 7.2,we immediately obtain
Proposition 7.3The stream functions(ψ,uz),defined by(6.5)
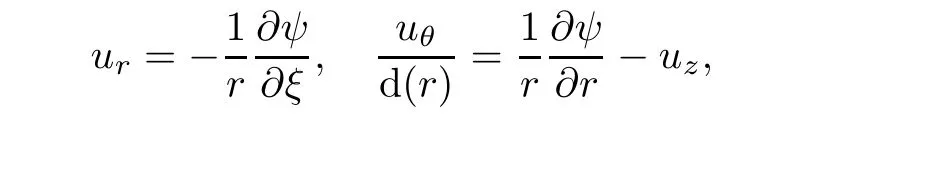
satisfy the following variational problem
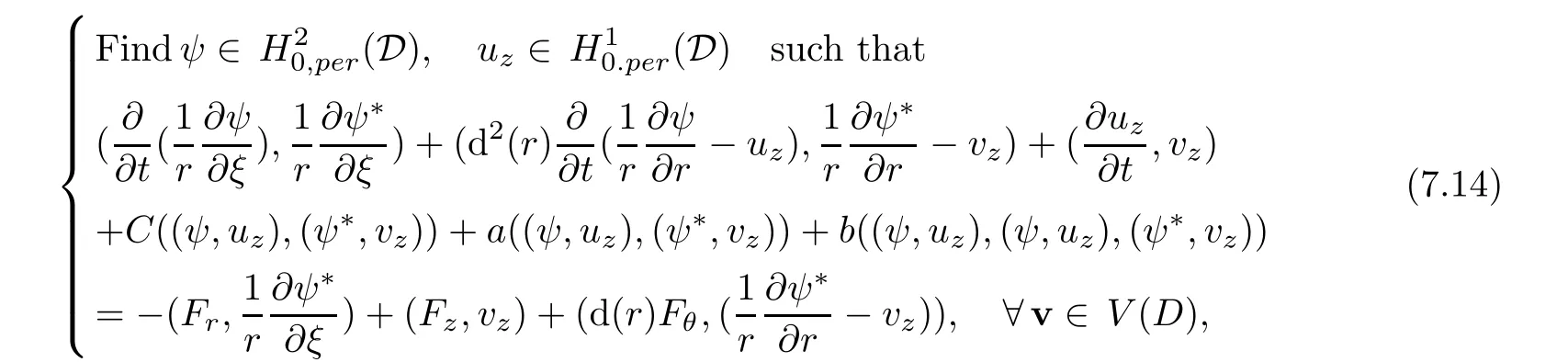
where
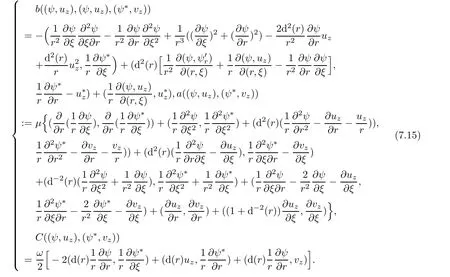
Here,to get the expression of a((ψ,uz),(ψ∗,vz)),we useand
Remark 7.4The norms of Sobolev spaces of L2(Ω),H1(Ω)in helical coordinate system are equivalent to the following norms
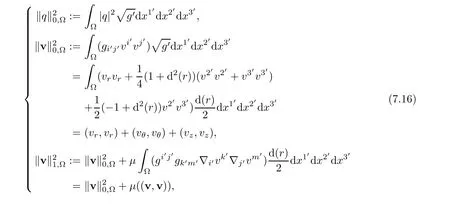
while

8 The Power and Propulsion of the Screw
The contravariant components and covariant components of total stress tensor acting on ΣHin helical coordinate are given by
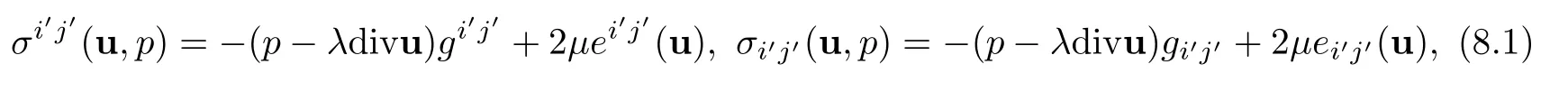
where covariant and contravariant components of strain tensor for the fluid velocity are given by

The normal stress vector and tangent stress vector with unit normal vector n and unit tangent vectorto ΣHare,respectively,
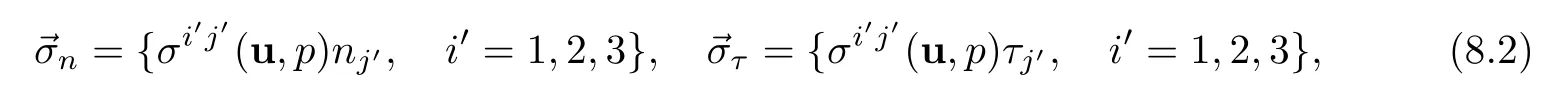
where ni′are contravariant components of n in helical coordinate
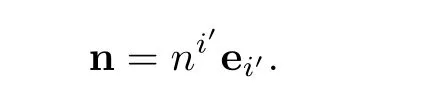
Because our assumption is the fluid to be incompressible,hence divu=0.Propulsion force T and Power rate W are

where er,eθ,k are base vectors of cylindrical coordinate system

It is clear that(8.3)shows that in order to find T,W,we have to give contravariant components of vector k,eθ,n.To do that,by virtue of(3.12)and(3.13),it is easy to obtain the following formulae:

In addition,reθ=e2= −rsinθi+rcosθj,that is,
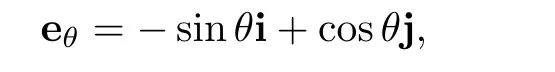
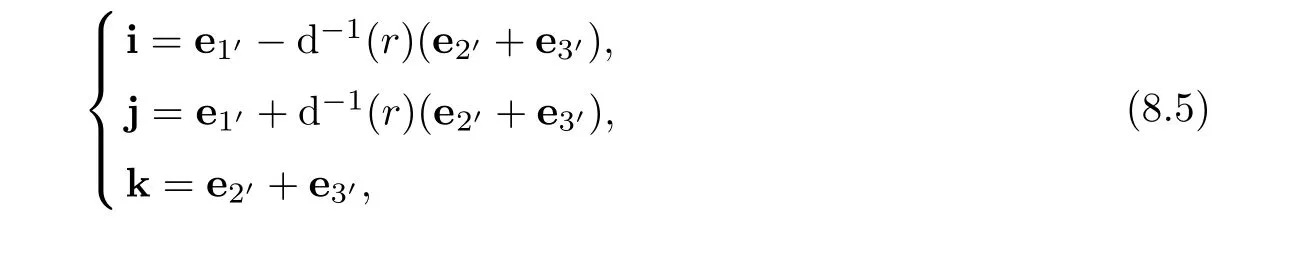

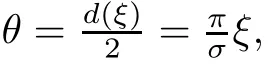
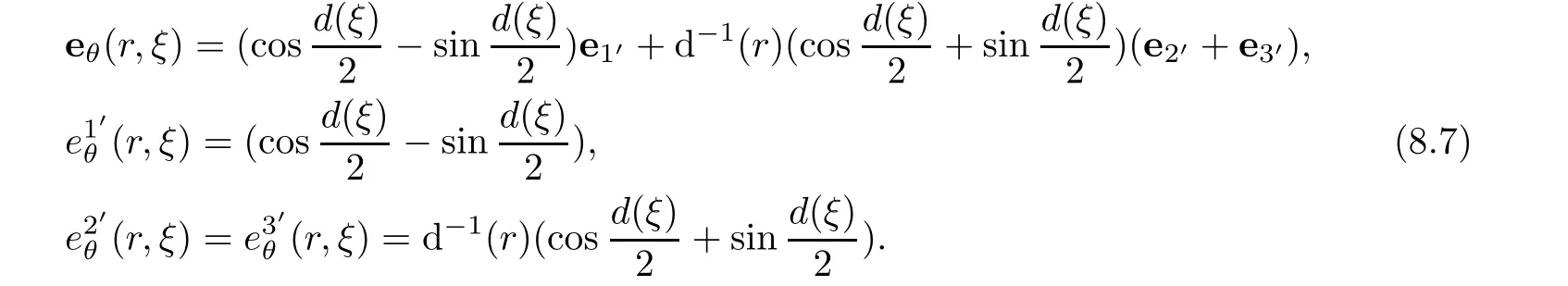
Next,we find ni′in helical coordinates.At the first,let S denote two dimensional manifold generated by helical coordinate lines x1′and x2′,and let TS denote the tangent plane spanning on based vector(e1′,(e2′)of helical coordinate system.The unite normal vector n to TS at point(x1′,x2′,x3′)is determinate by

By virtue of(3.12),
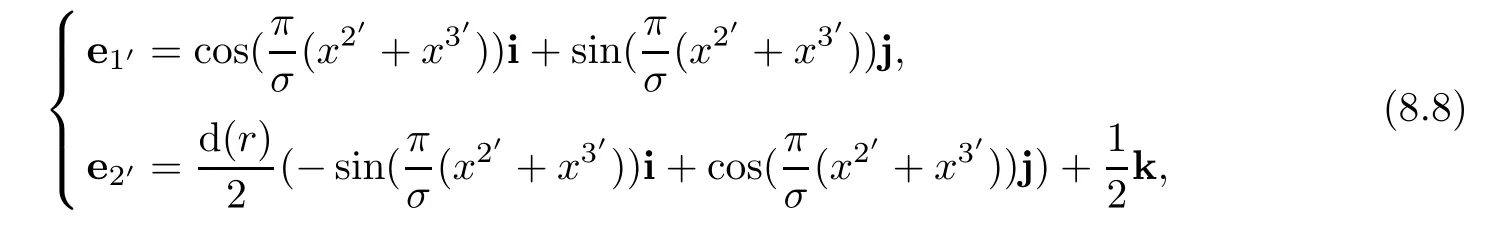
we assert that
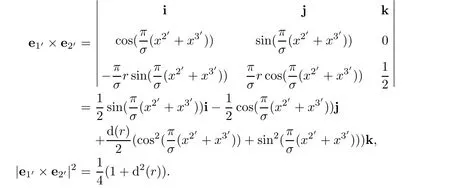
Therefore,we have
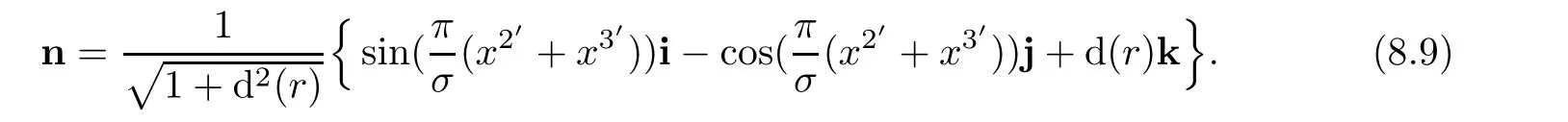
On the other hand,solving(i,j,k)in terms of(ei′,i′=1′,2′,3′)from(3.12)leads to

Taking(8.9)and(8.10)into account,it yields by simple calculations that

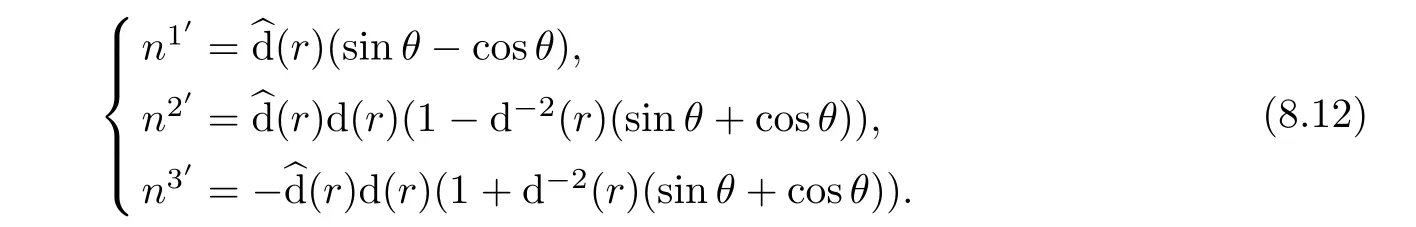
In particular,consider the normal vector at helicoid surface x3′=0.Let ξ=x2′,thenWe assert
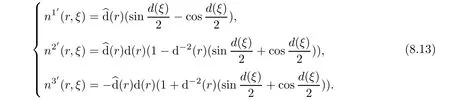
Let us return to(8.3).At the first,we consider incompressible flow.By virtue of(8.7)and(8.13),we have
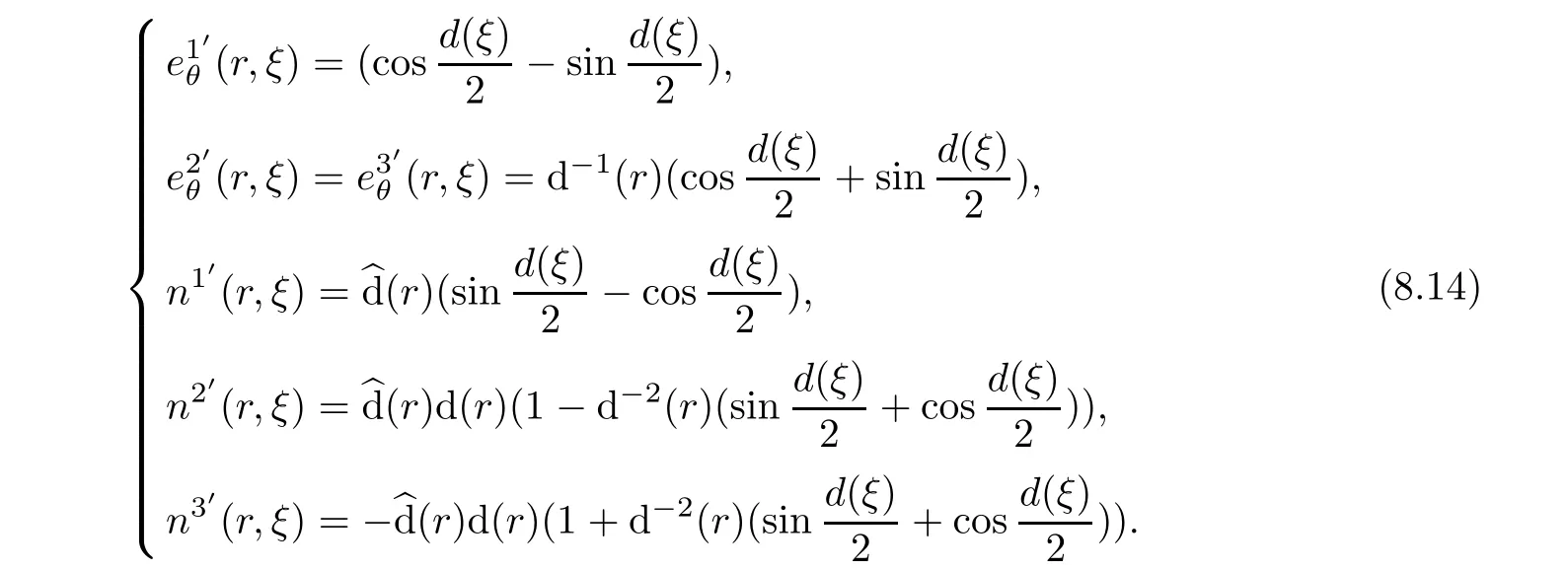

At the first,by computing,we have

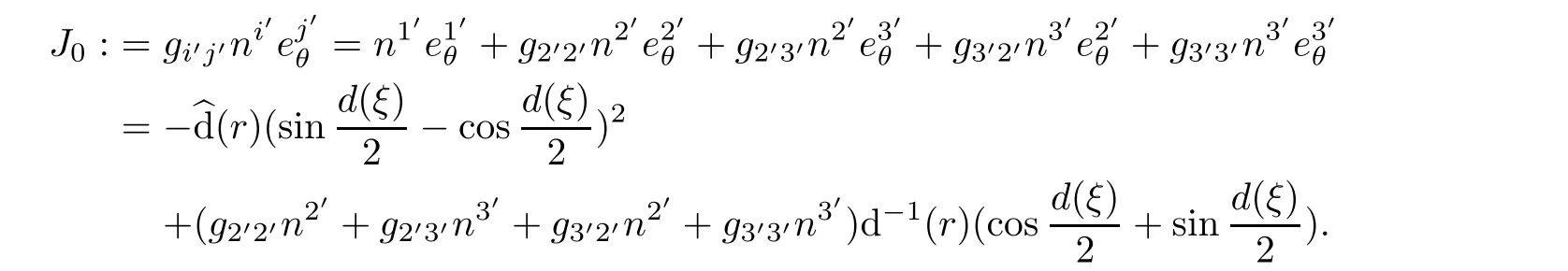
(3.14)shows
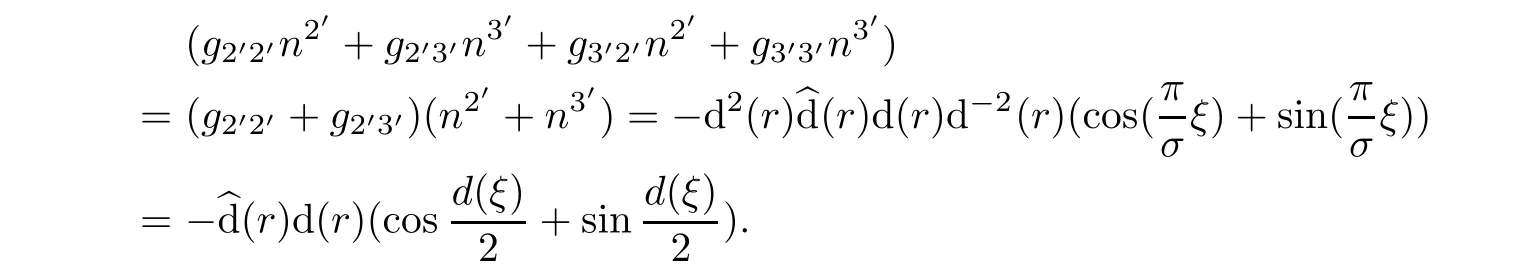
It yields that
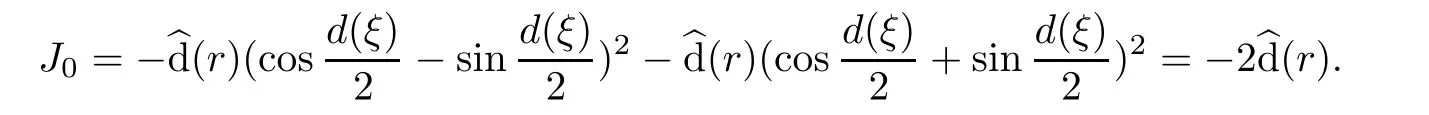
Finally,we assert
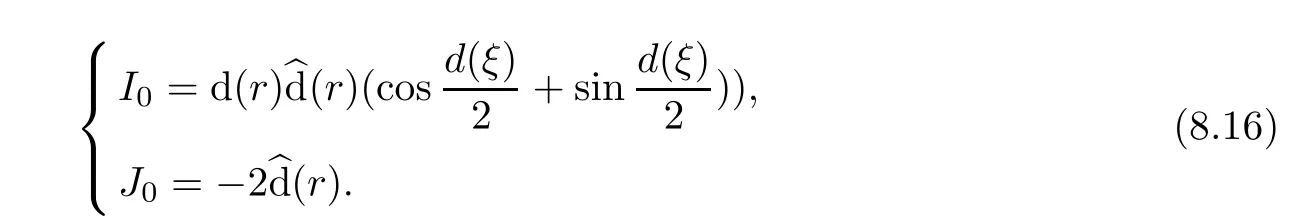
By virtue of(3.14)and(4.4),we have


To sum up,we assert
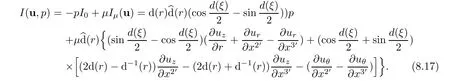
Next,taking(8.14)into account,we get
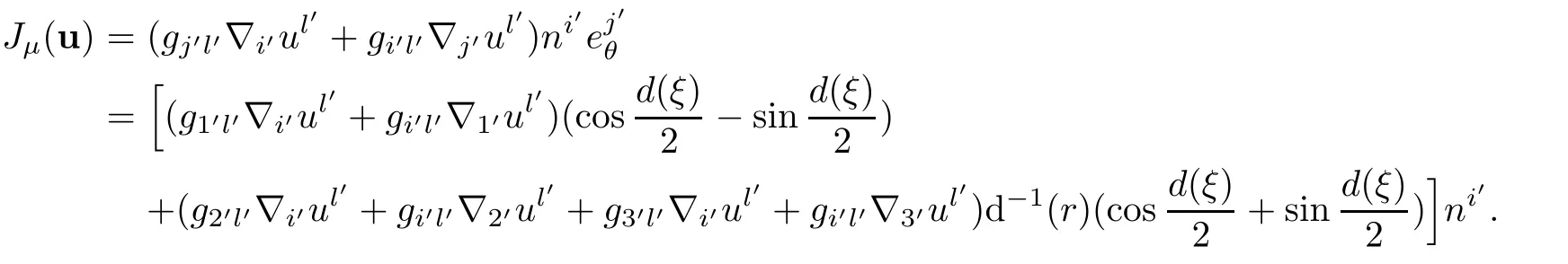
Calculations show that

From this,it yields
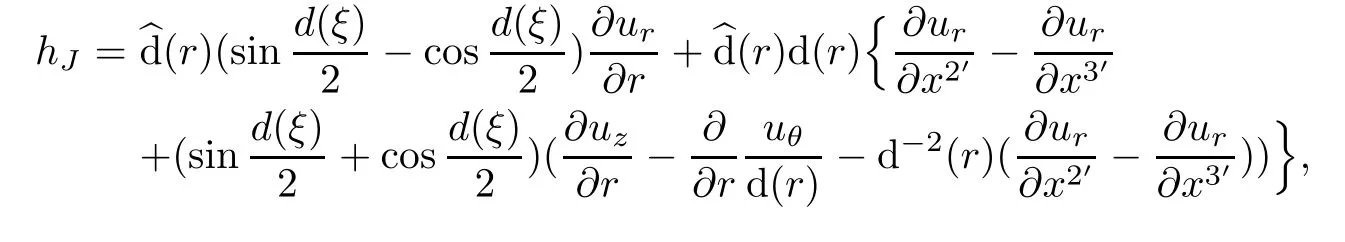


Therefore,
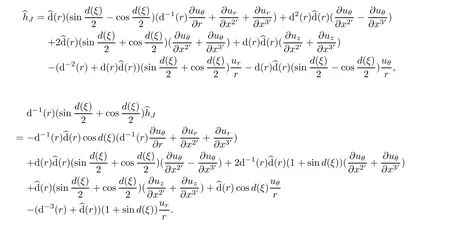
Hence,we find

So,owing to J(u)=−J0p+µJm(u),we have
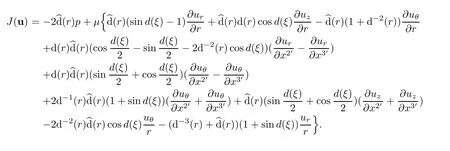
Thus,we obtain

Finally,we conclude
Proposition 8.1For the helical flow,the power T and propulsion W defined by(8.3)can be computed by the following formulae

where I(u,p)and J(u,p)are given by

If the flows are helical,then

which can be expressed in terms of stream functions,
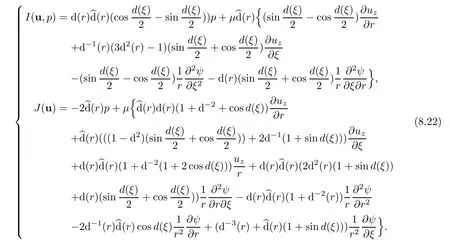
9 Stokes Operator and its Eigenvalue Problem in Helical Coordinates
We consider the following Stokes equations with mixed boundary conditions,that is,periodic in the z-direction and homogeneous Dirichlet on the surfacesof the cylinder and the helicoid.It is well known that Stokes equations are an invariant form in any curvilinear coordinate system.For the homogeneous Dirichlet boundary conditions on whole boundary∂Ω,what follows that we set

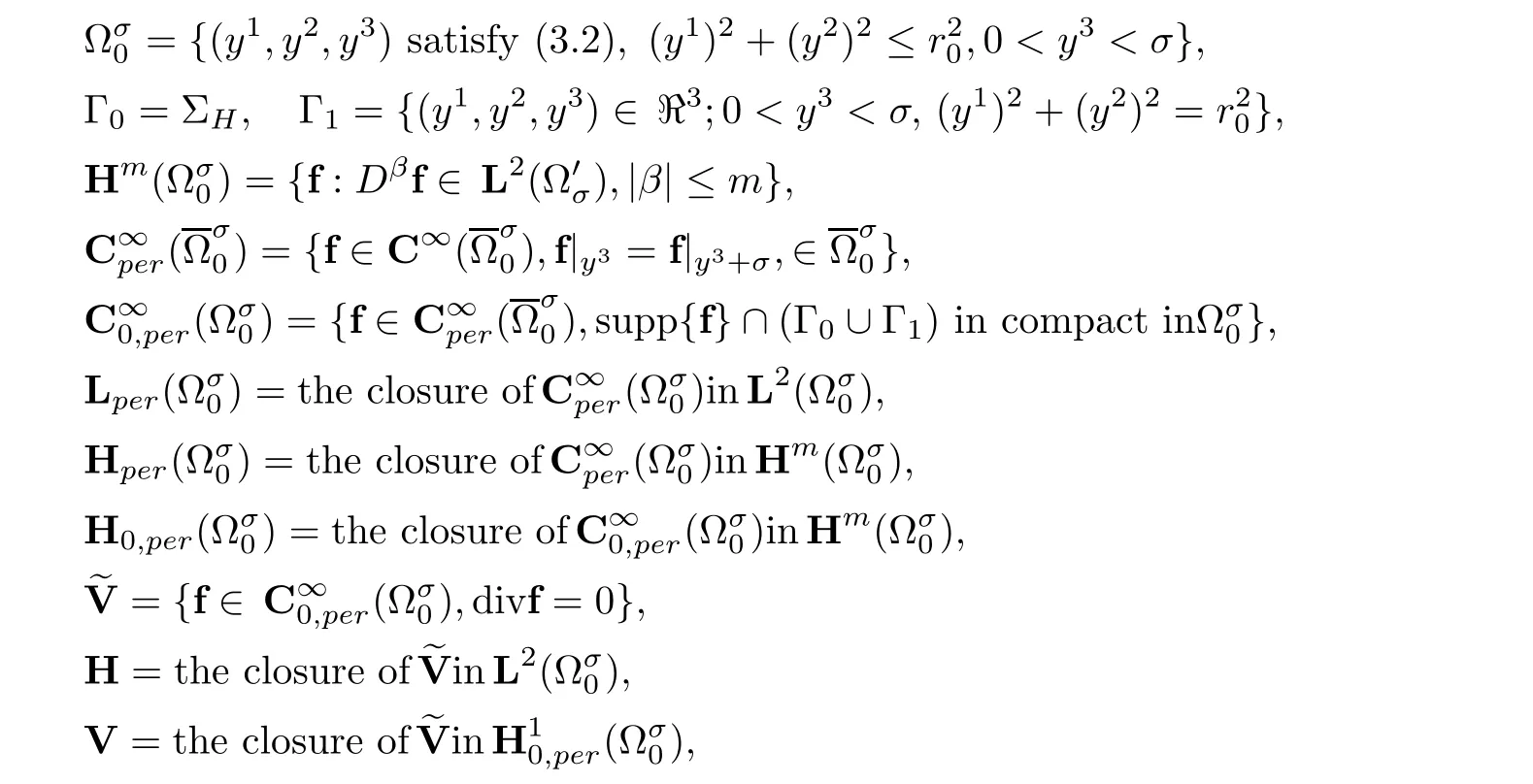
where(y1,y2,y3)are Cartesian coordinate.
In[2]Constantin and Foias established existence,uniqueness and regularity results,and proved that Stokes operator is self-adjoint and positive definite and there exists a compact inverse operator of the Stokes operator.Therefore,there are complete orthogonal system of eigenfunctions for the Hilbert space H.On the other hand,there is a diffeomorphism mapping from Ωσ0into a solid torus T in R3in which Stokes equations can be expressed as
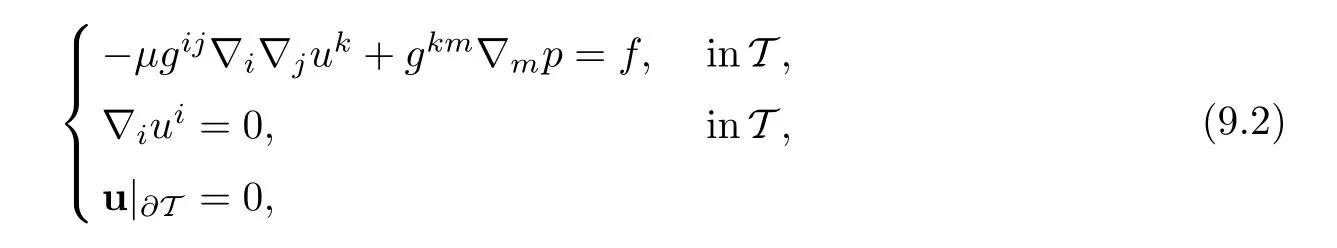
where gijare contravariant components of the metric tensor of R3in a certain coordinate,∇iare covariant derivative operator.Because of positive definition of metric tensor gij,equations(9.2)are an elliptic partial equations.Therefore,there are similar results for(9.2)(see[1]and[4]).In(9.2),u is required to satisfy only the homogenous boundary conditions sine the C∞-diffeomorphism,which provides the equivalence between(9.1)and(9.2),identifies the top and the bottom of,that is,identifies the disk{gap of(with the disk{gap ofBy virtue of results in[2],we could establish existence,uniqueness,and regularity(see[11]).
Theorem 9.1LetThen,there exists a uniqueandsatisfying Stokes system(9.1).Moreover,
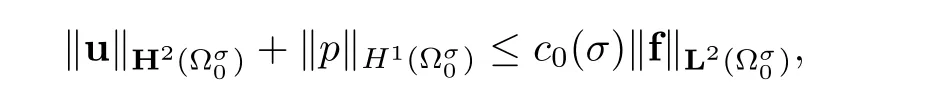
where cσis a constant which depends only on σ.
Moreover,the abstract Stokes operator can be defined by A=−P△,which is symmetric and self-adjoint and has a compact inverse operator A−1,and there exists a sequence of positive eigenvalues 0< λ1≤ λ2···≤ λj≤ λj+1≤ ···and a sequence of corresponding eigenfunctions uk,k=1,2,···,Auk= λkuk.
Next,let us consider eigenvalue problem of Stokes equations with mixed boundary conditions in helical coordinates.By virtue of(6.4)and(6.9),we obtain eigenvalue problem for(u,p)and stream functions

Proposition 9.2The stream functions(ψ,uz),defined by(6.5),that is,and,satisfy the eigenvalue problem associated with(9.3),

(9.4)can be rewritten as
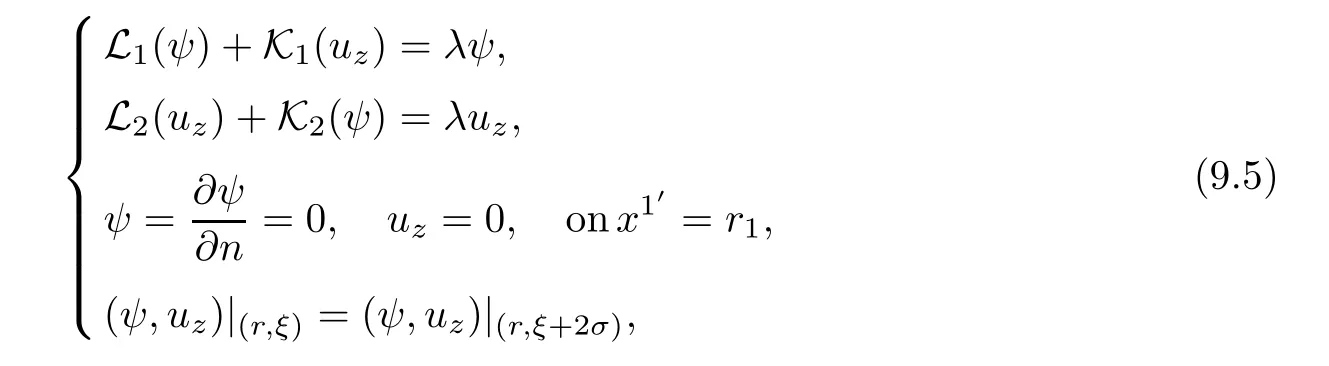
wher e
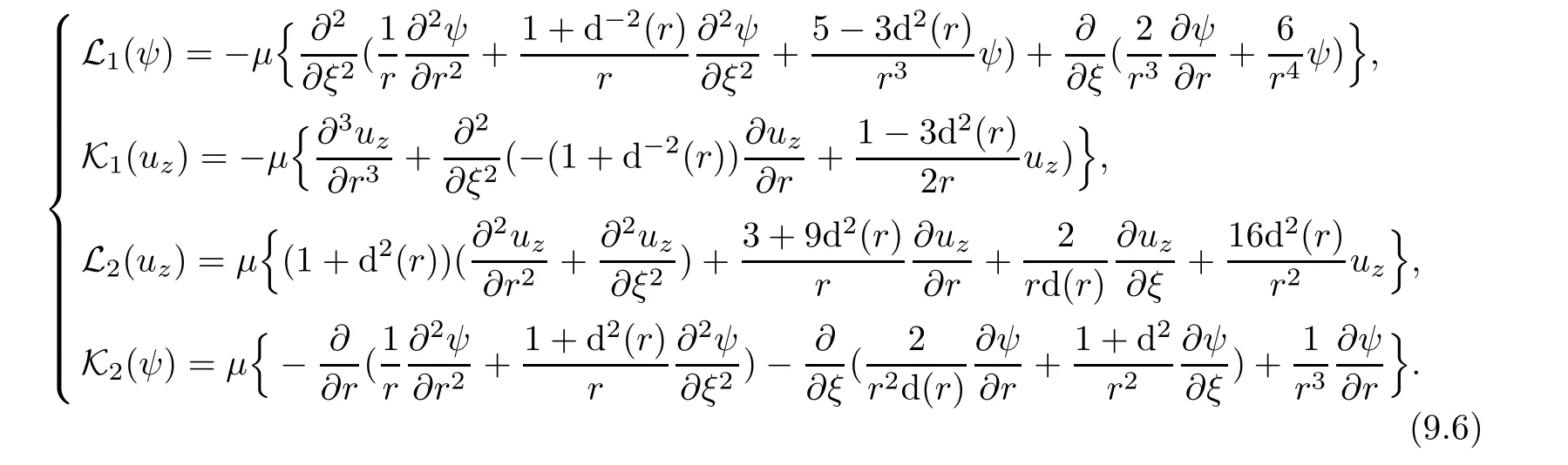
Associated variational formulations is given by

wher e
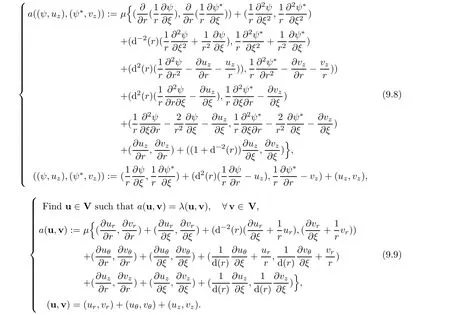
There are in finite eigenvalues 0< λ1≤ λ2≤ ···of eigenvalue problem(9.3),therefore for(9.7),we have corresponding helical eigenfunctions uk∈ H and(ψ,uz)∈ V.Because vector u=(ur,uθ,uz),pressure p,and(ψ,uz)∈ V are periodic functions with periods 2σ with respect to variable ξ,we assume that

Substituting(9.10)into(9.8),taking orthogonality of Fourier functions and noting
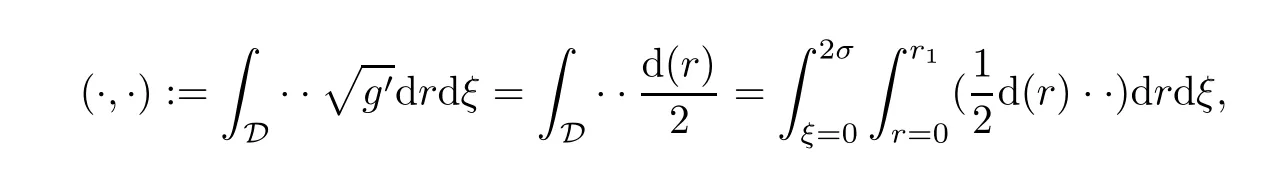
we obtain
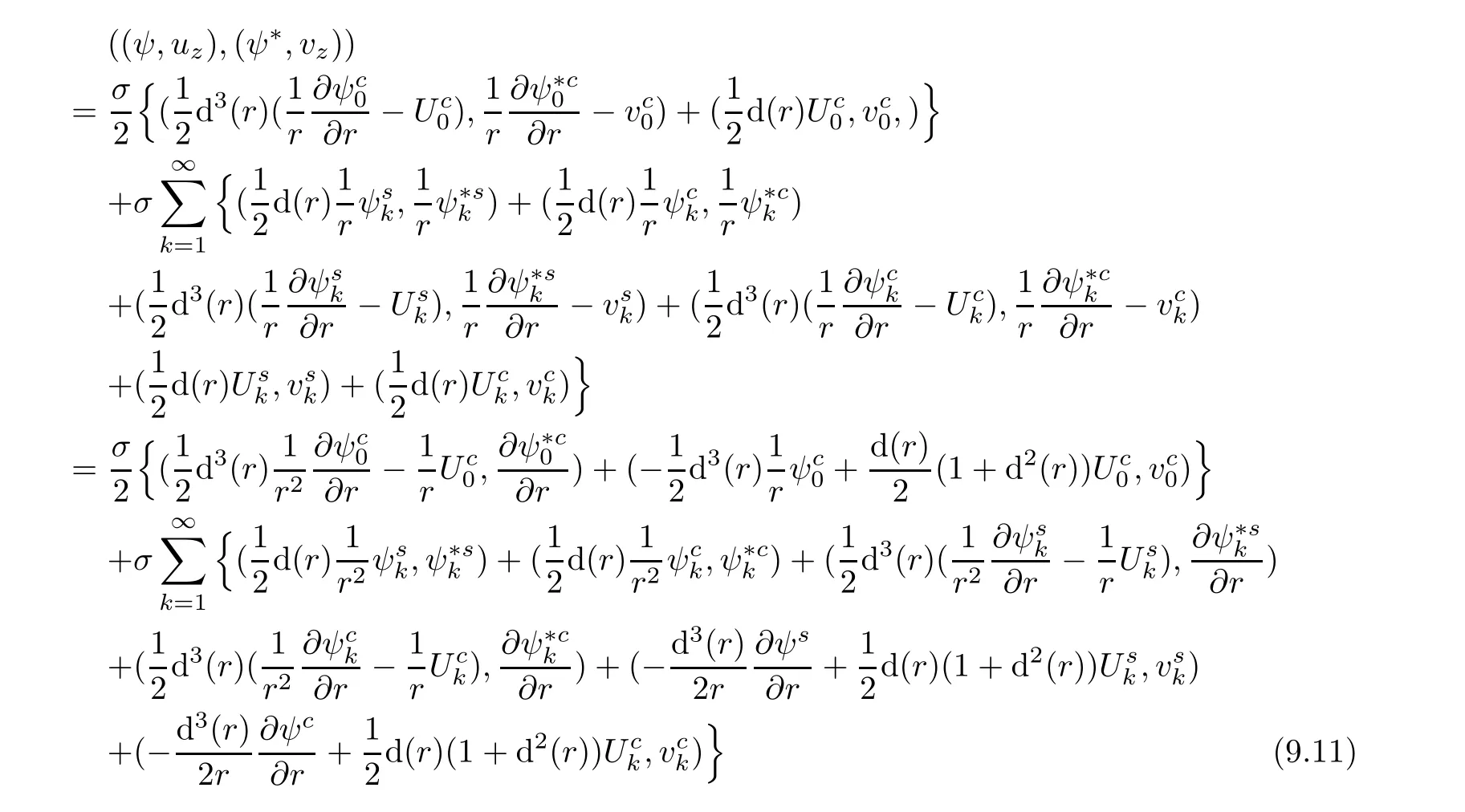
and
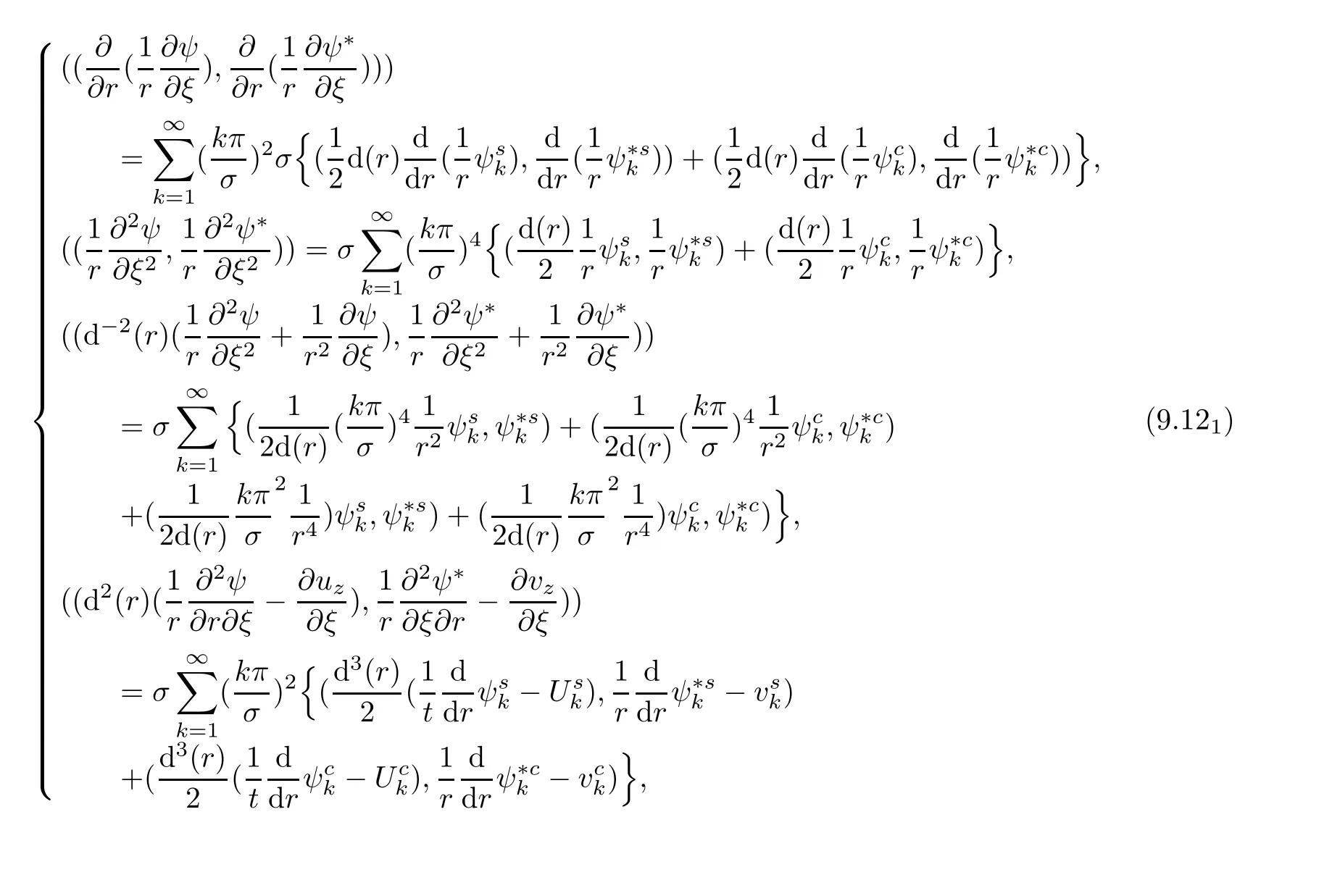
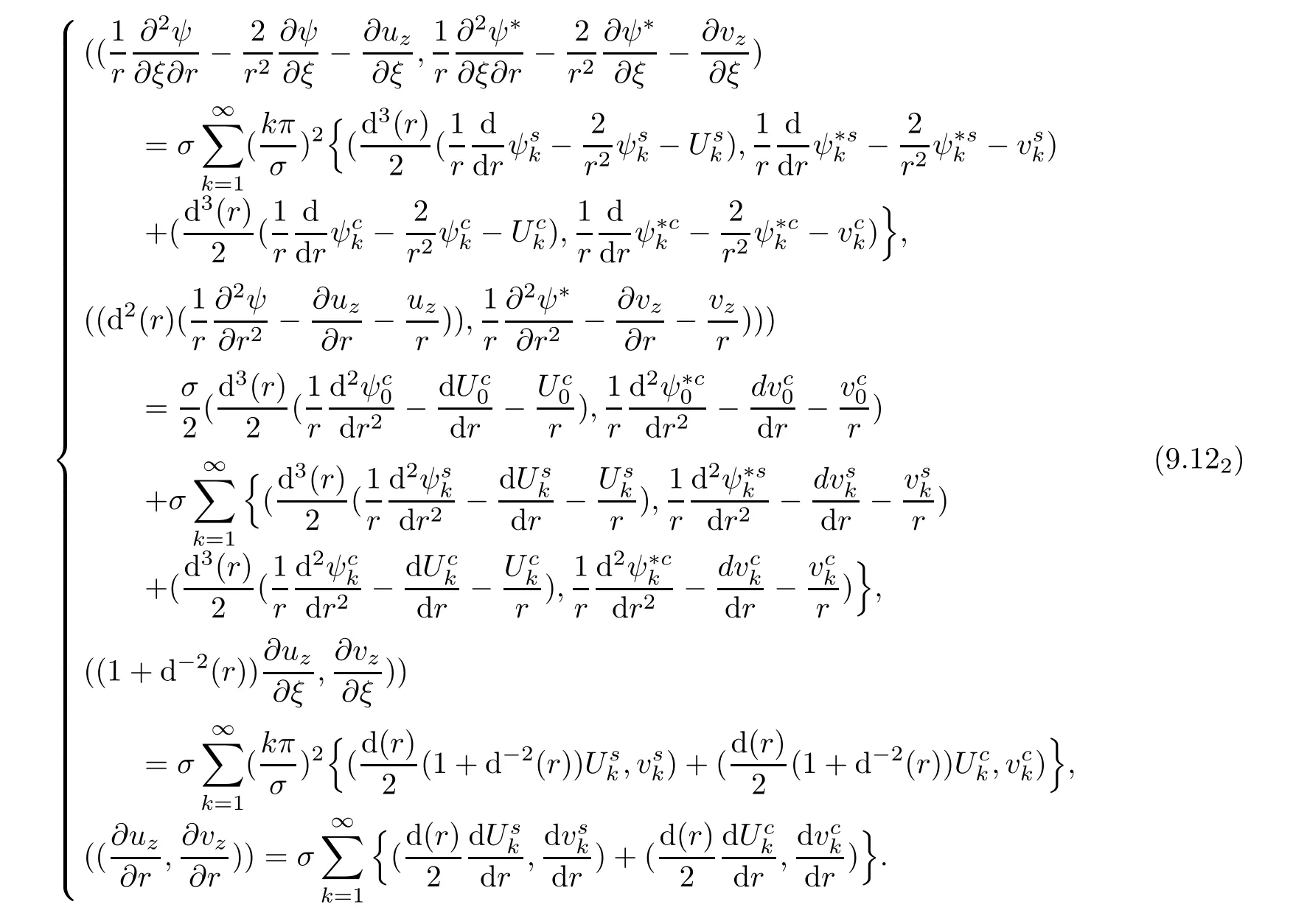
Combining(9.8),(9.11)and(9.12),we find

Simple calculations show that
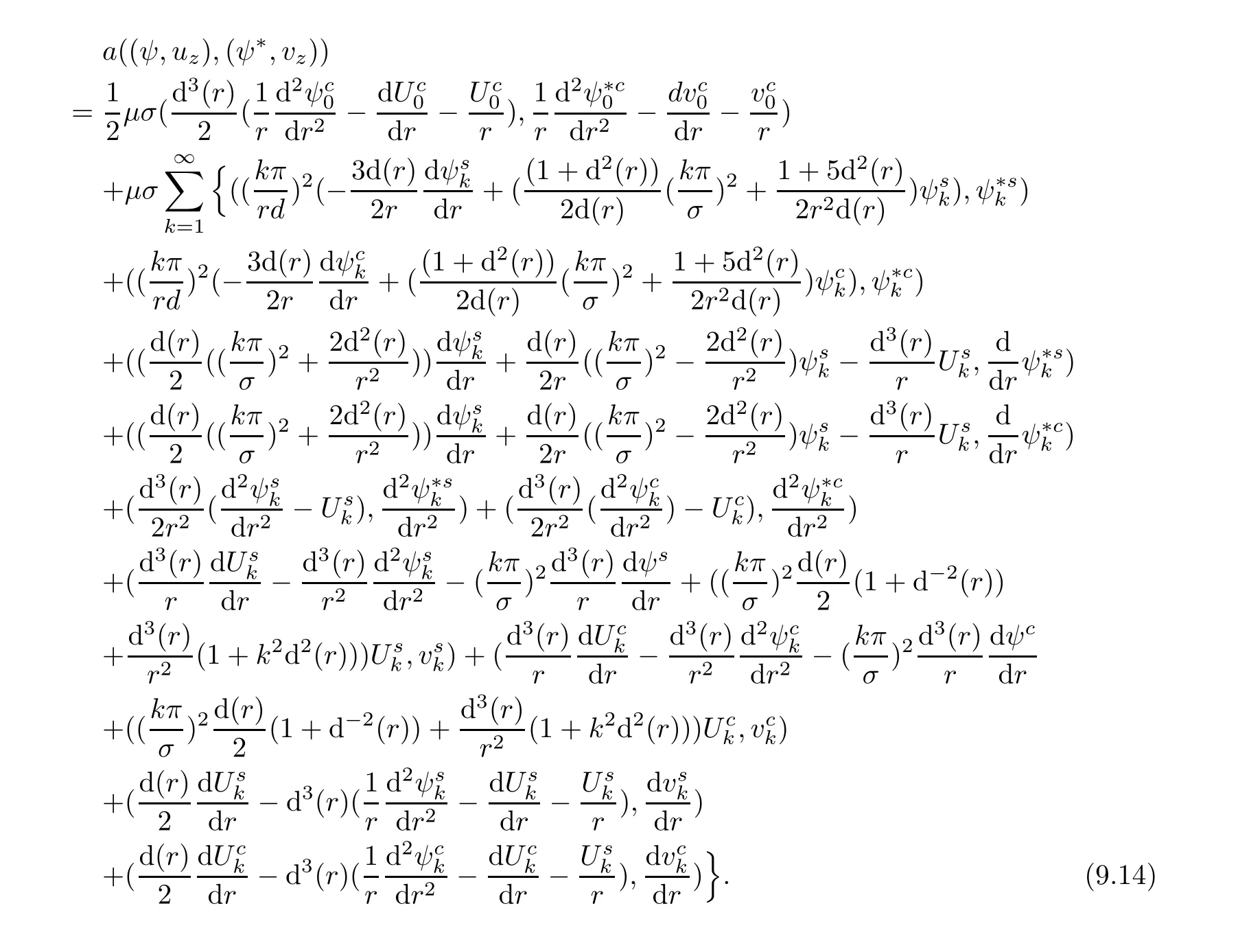
Because Fourier functions are independent and complete in Sobolev spaces,taking(9.11)and(9.14)into account,we obtain


Because
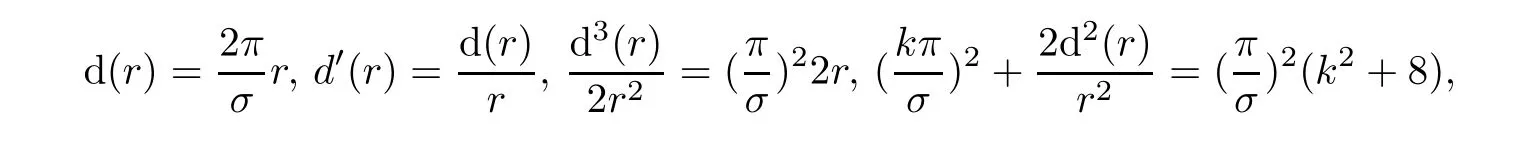
from(9.16),we assert

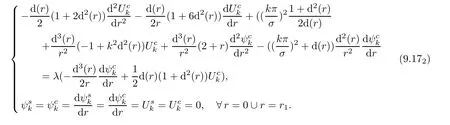
 Acta Mathematica Scientia(English Series)2018年3期
Acta Mathematica Scientia(English Series)2018年3期
- Acta Mathematica Scientia(English Series)的其它文章
- INITIAL BOUNDARY VALUE PROBLEM FOR A NONCONSERVATIVE SYSTEM IN ELASTODYNAMICS∗
- LONG-TIME DYNAMICS OF THE STRONGLY DAMPED SEMILINEAR PLATE EQUATION IN RN∗
- STABILITY OF TRAVELING WAVES IN A POPULATION DYNAMIC MODEL WITH DELAY AND QUIESCENT STAGE∗
- NONLINEAR STABILITY OF VISCOUS SHOCK WAVES FOR ONE-DIMENSIONAL NONISENTROPIC COMPRESSIBLE NAVIER–STOKES EQUATIONS WITH A CLASS OF LARGE INITIAL PERTURBATION∗
- A GENERALIZATION OF GAUSS-KUZMIN-LÉVY THEOREM∗
- THE EVENTUALLY DISTANCE MINIMIZING RAYS IN MODULI SPACES∗
