基于Harmonic函数的自动试题标注模型
谢 莹,许荣斌
(安徽大学 计算机科学与技术学院,合肥 安徽230601)
在目前的高校教学评价工作中,课程科目繁多,试题量大,组卷工作任务繁重.自动试题标注是指在组建试题库时对小部分试题进行关键词分类标注,建立一个模型,新加入的试题可以通过此模型进行自动标注分类.这项工作可以减轻教师题库建设的工作量,亦可发展此模型对试题得分率进行预测,从而控制组卷的难易程度.由于人工标注样本代价很大,自动试题标注工作对文本快速索引和检索系统有着重要的意义[1].
文本标注问题在近10年一直较为活跃,也产生了一些有效的方法.研究文本自动分类的核心问题是如何构造分类函数(分类器),分类函数需要通过某种算法进行学习获得.分类是重要的数据挖掘方法,在众多的文本分类算法中,目前主要有改进的 Rocchio 算法[2]、改进的贝叶斯分类算法[3]、K-近邻算法[4]和支持向量机的知识组织算法[5].近年来邬开俊等将遗传算法和并行协同进化算法结合起来,在粗糙集的基础上设计了一个并行协同进化遗传算法,并将该算法用于文本特征选择.该方法采用遗传算法搜索特征,利用并行协同进化算法来提高时间效率,从而较快地获得较具代表性的特征子集[6].何跃等提出了一种改进的以访问时间、点击次数以及访问路径共同刻画用户的访问兴趣的Web日志挖掘算法.首先以Web日志为基础构建相关矩阵,使用平均访问时间相似度和访问路径相似度共同度量用户访问兴趣的相似程度,最后采用直接聚类去除相交项的聚类算法将相似用户和相关URL聚类[7].
在文本标注存在的方法中,最简单的是将标注问题看做一种特征空间重建[8].最常见的方法是使用K-近邻方法及扩展来分配关键字.如基于选择相关距离,使用稀疏逻辑回归的方法,如LASSO方法[9].实践效果上,平均距离方法比加噪LASSO方法在标注精度上会更好.目前所提出的一些方法都较少对训练样本文本的关键字和类区域之间的相应关系进行深入研究.本文分析标注数据的特点,构建描述数据序列相似的对称权矩阵,结合基于图的拉普拉斯算子方法,采用约束化Harmonic函数,进行自动试题标注工作.
1 模型的提出与分析
1.1 自动试题标注工作框架
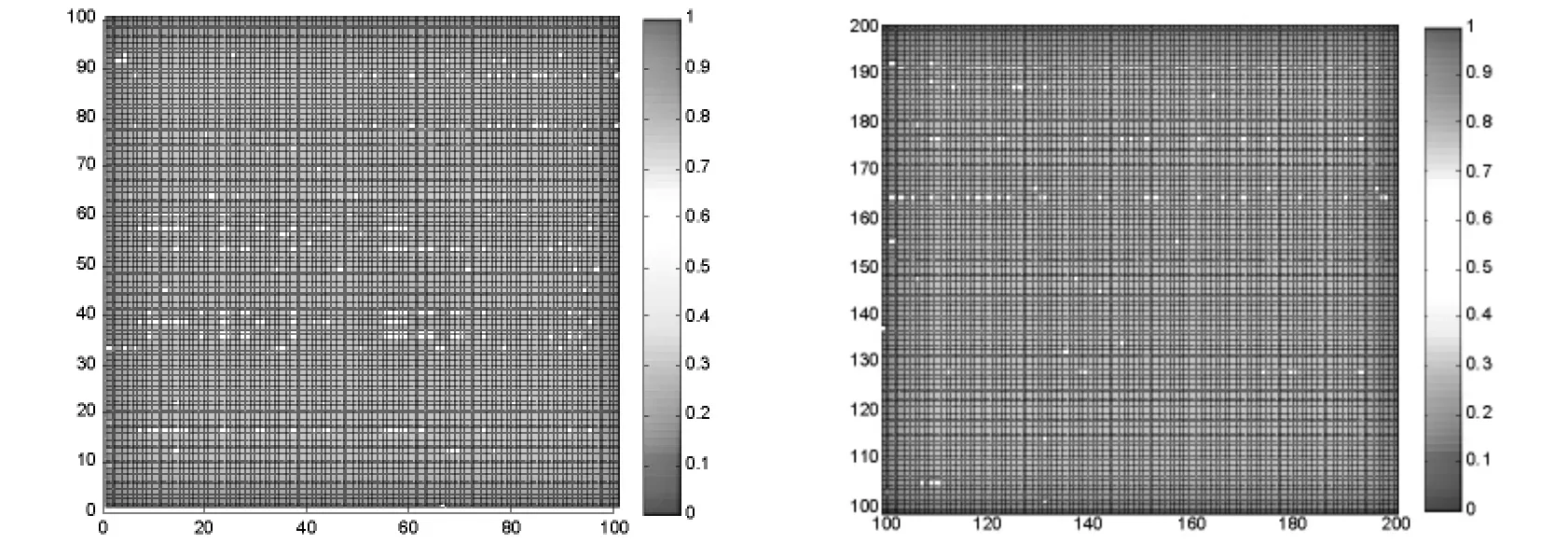
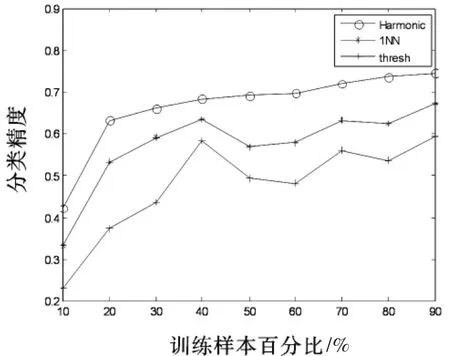
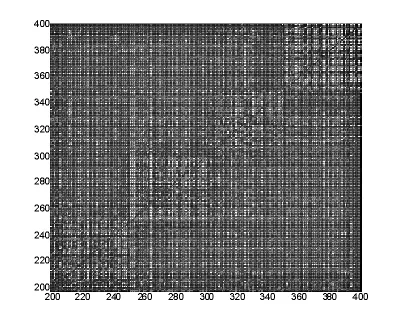
在自动试题标注工作中,假设标注总试题样本数目为n,其中l个样本是已标注样本,u个样本为未标注样本.一般而言,在实际工作中,已标注样本个数应远小于未标注样本的数目,即l 在全部n个结点上定义n×n对称权矩阵W=[wij]: 其中xi∈Rp,p是单个样本的维度.xi是原始数据X的第i个样本.基于以上定义,W是一个具有非负元素的正定矩阵,存储了n个数据序列的相似性信息,在欧式空间中相近的点在W矩阵中将会赋予较大的边权[10-12]. 设定D为W的对角度矩阵,Dii=∑jWij.基于图的组合拉普拉斯算子Δ定义为: 本文将W中的节点以(x1,…,xn)序列映射到1-D空间中.若i,j点是相似节点,即Wij较大时,i,j节点在映射空间中是连接的,则(xi-xj)2值较小,可得到目标方程如下: 若向量x在其维度上没有约束,则当xi=0时将会得到最小值.但是这个结果显然不符合要求,需要对xi进行规则化约束为∑ixi2=1.若将xi替换为xi+a时,为了使得目标方程值仍不发生改变,对xi再加上约束为∑xi=0,此时xi中必然含有混合元素. 基于以上两种约束,映射问题转变为: 映射问题(3)的解较易求得,由于: Δ算子如前定义,称为图拉普拉斯,最小化映射目标的映射解由下式的特征向量决定: 拉普拉斯映射广泛使用于机器学习工作,作为保留局部拓扑结构而映射图节点的正则化方法. 本文将在连通图G=(V,E)上计算实值函数f(i)=yi,i∈1,…,l.基于函数f对未分配类标试题集进行自动标注工作.本文的目的是希望未加标签的数据点在同类条件下应该相似,可以基于式(3)定义代价函数: 研究发现,最小代价函数f=arg minf|L=ftE(f)是满足Harmonic属性的. 属性1:在未标签数据点集UU上满足Δf=0,在已标签数据集L上亦满足此属性.Δ=D-W为如前定义的组合拉普拉斯算子.D=diag(di)为对角矩阵,每一个元素di=∑jWij,而W=[Wij]为权矩阵. 属性2:在每一个未加标签的数据点f的值是邻近点的均值: 将 f的表达做一些修改:f=Pf,其中P=D-1W.基于Harmonic函数的最大原则[13],f是唯一的并且满足0<f(j)<0,其中 j∈U. 为了将Harmonic函数直接应用于自动试题标注,采用矩阵算子,将权矩阵W分为4块: 基于Harmonic函数f来求解未标签数据的标签值,最简单直接的阈值判别准则是: 本文将基于Harmonic函数(10)及阈值判别原则(12)对图像数据进行自动标注工作. 第一步:读入数据集数据得到统计数据集X∈Rp*n,读入类别数K,读入每类样本数m,设定训练样本比率,每类中学习样本为ln,标准样本为un. 第二步:获得学习样本矩阵dataMatrix∈Rp*n,获得标注样本矩阵queryMatrix∈Rp*un,重新建构数据矩阵X,使得X的前ln×K个列向量为未标注样本,其余为学习样本. 第三步:依据式(1)计算相似度矩阵W;计算图拉普拉斯算子Δ=D-W,D=diag(di)依据(10)计算Harmonic函数fu. 第四步:利用阈值原则(12)计算自动标注精度. 准则(11)在类与类之间分隔较好的情况下,效果会比较好.而在实际数据应用中,类与类之间经常并不是理想分隔,这时再应用准则(11)易产生较为严重的错误标注结果. 对矩阵W进行研究发现,由于W是数据流形结构的存储矩阵,在实际应用中往往比较难计算,并且不能反映标注工作.将考虑类标优先准则,假设类1所占比例为q,类0所占比例为1-q,利用类群正则化来调整类分布,以此更好的取得精确的标注结果. 定义类1群为∑ifu(i),类0群为∑i(1-fu(i)).类群正则化度量了类群,若未标签数据点i满足条件(12),模型(10)将会把数据点i分配给类1,否则将数据点i分配给类0. 本文采用程序设计试题数据集进行实验工作.将计算机程序设计基础课程的数据集以知识点的形式建立.在正式组卷时可以设定为选择题、填空题、简答题及程序编程题.试题数据集S中每条记录具有一个标签,共20个标签,标签集合为:程序设计基本概念、对象的概念、数据类型、变量与常量、运算符和表达式、常用内部函数、顺序结构、选择结构、循环结构、程序调试、数组的概念、静态数组及声明、数组的基本操作、常用算法、函数过程的定义和调用、子过程的定义与调用、参数传递、过程和变量的作用域、控件设计、常用的文件操作语句和函数.数据集共有1 000个试题条目,每一个条目具备若干个关键字并归属于某一标签类别.数据集特征空间如图1所示,左图展示了第一类的数据集特征空间,右图展示了第二类的数据集特征空间.从两图对比可以看出,各类内的数据特征较为统一,类内相似度较高. 图1 试题数据集特征空间 本文采用 Term frequency-inverse document frequency(TF-IDF)方法[2]对试题库进行统计工作.TFIDF是一种用于资讯检索与资讯探勘的常用加权统计方法,用以评估一个字词对于一个文件集或一个语料库中的其中一份文件的重要程度.字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降.TF-IDF加权的各种形式常被搜寻引擎应用,作为文件与用户查询之间相关程度的度量或评级. 在本文给定的试题文件里,由于词频 (TF)是某一个给定的词语在该文件中出现的次数,这个参数将会进行归一化工作,以防止它偏向长的文件(同一个关键词在长试题里可能会比短试题有更高的词频,而不管该关键词重要与否).而逆向文件频率 (IDF)将测试关键词普遍重要性.试题集内的高词语频率,以及该词语在整个试题集合中的低文件频率,可以产生出高权重的TF-IDF.因此,TF-IDF将在试题库中过滤掉常见的关键词,保留重要的关键词. 本文采用1-NN方法和thresh方法作为比较方法,对Harmonic方法的自动试题标注精度进行比较分析.1-NN方法即在半监督分类时采用数据点1近邻来进行分类工作,而thresh方法即采用公式(11)进行阈值选择来分类. 采用k次交叉验证方法对实验精度进行测量,初始采样分割成k个子样本,一个单独的子样本被保留作为验证模型的数据,其他k-1个样本用来训练.交叉验证重复k次,每个子样本验证一次,平均k次的结果,最终得到一个单一估测.这个方法的优势在于,同时重复运用随机产生的子样本进行训练和验证,每次的结果验证一次.当已加标签数据量增加,即参与学习的数据量增加时,标注精度也总体随之增加.如图2所示.在较常使用的10-交叉验证法中,数据集在Harmonic方法下标注精度达到42.3%,1-NN方法达到33.2%,而thresh方法达到23.1%;当训练样本百分比达到20%时,即在5-交叉验证法测量下,数据集在Harmonic方法下标注精度达到63.3%,1-NN方法达到53.2%,而thresh方法达到37.1%. 图2 试题数据集在不同已加标签数据量下的标注精度图 在已加标签数据量达到总数据量的50%和80%时,1-NN方法和thresh方法的标注精度均有不同程度的下降,出现“粘滞”现象.而Harmonic方法则较为平稳上升.分析发现,在学习样本所占比例较大的情况下,拉普拉斯映射的学习能力较为稳定. 由于原始数据是经过TF-IDF方法得到的统计数据矩阵较为稀疏,不能采用传统的RBF相似度度量方法,即在全部n个结点上定义n×n对称权矩阵W=[wij]: 其中xi∈Rp,p是单个样本的维度.xid是xi的第d个成分. 若采用RBF相似度度量法,得到的相似度矩阵无明显类块特性.考虑到以上情况,本文采用Cosine相似度度量,即: 得到的相似度矩阵如图3所示. 从图3中可以明显看出,由于本数据集是每类50条试题,从而相似度矩阵中具备K个50*50的类块结构,K为类别总数.表明相似类特征较为集中,这样的相似度矩阵有利于分类工作的展开. 研究发现,从Harmonic方法得到的未标签数据集应同样具备类块特性.在5-交叉验证下解得的数据图如图4所示.从图4中可以看出,求出的未标签数据集相似类特征亦较为集中,聚类效果良好. 图3 数据集相似度矩阵部分示意图 图4 数据点矩阵部分示意图 高等院校教学工作中,组卷试题库中试题量巨大,科目繁多.为加速自动组卷工作,减轻人力标注成本,本文结合拉普拉斯映射和Harmonic方法,将其应用于半监督试题自动标注,这项工作采用拉普拉斯算子将原数据映射到低维空间中,采用Harmonic函数作为自动图像标注模型,新方法具备Harmonic属性,利用数据相似度矩阵和基于图的拉普拉斯算子分析数据结构,强化数据类块特性. 实验证明此方法确实在自动试题标注精度上有很好的效果,标注精确度均高于1-NN方法和阈值选择方法,具备有效性.但在实验中发现,降维的维度控制对标注的准确性存在很大的影响.下一步,可以研究如何控制降维维度与标注准确性,使得两个指标之间取得较好的平衡;并研究如何在试题集中训练得分预测模型,用于预测与控制组卷后试卷的难易程度.这项工作的开展,有利于教师将检测评价的工作再反到教学工作中去,对课程教学亦具有很好的实际意义.1.2 基于图的拉普拉斯算子



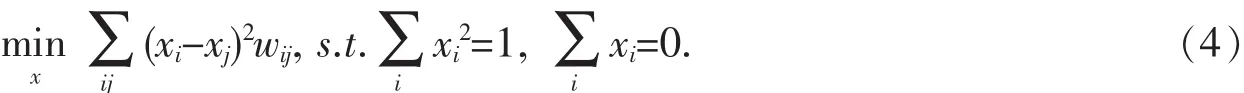


1.3 Harmonic函数的基本理论




1.4 类群正则化


1.5 算法流程
2 自动试题标注实验分析
2.1 实验数据集描述
2.2 TF-IDF方法
2.3 相关方法的自动试题标注效果的比较与分析
2.4 类块特性



3 结论

