声表面波微力传感器信号处理电路的设计与仿真*
李济同,李媛媛*,卢文科(.上海工程技术大学电子电气工程学院,上海 060;.东华大学信息科学与技术学院,上海 060)
声表面波(简称SAW)最初在18世纪50年代地震波的研究中被发现,直到20世纪60年代,随着对SAW性质的熟知和环境因素对其影响特性研究的进展[1],SAW微力传感器的研究渐渐得到发展。这是一种结合了声表面波技术、薄膜技术以及电子技术的新型传感器[2],它通过敏感元件感应微力,根据敏感元件频率的改变实现对微力的测量[3],具有准数字输出、微型化、可无线无源化、多参数敏感性、结构工艺性好等特性[4]。
随着SAW微力传感器应用领域不断拓展,测量环境日趋复杂[5],信号处理电路的研究显得尤为重要。SAW微力传感器的检测通常基于对SAW相位、频率、幅值等参数变化的检测来完成[6],因此振荡电路的设计也是核心环节。2002年,Jason D S[7]提出采用DDS和PLL技术对SAW传感器输出信号进行检测。2004年,辛长宇[8]对DDS技术提出改进。2005年,Rasol A H[9]提出模拟与数字结合的方法的设计方案。2007年,张亦[10]研究了改进的皮尔斯振荡器对SAW传感器信号进行处理。2011年,康迤[11]设计一种基于多条耦合器的SAW振荡电路;Nordin A N[12]提出高频CMOS-SAW振荡器改善插入损耗和相位斜率。
通过前期的研究对比发现,信号处理电路性能的提升可以通过振荡电路的设计以及检测方案的优化实现。本文采用混频检测法,设计两路新型SAW振荡电路,将参考振荡电路和检测振荡电路产生的信号送入混频电路求出频差[13]从而实现对微力的检测。在混频检测法的电路优化问题中,振荡电路的灵敏度、噪声干扰抑制、高频稳定性;滤波电路的增益平稳度、衰减带下降速度也是研究的重点。
1 信号处理电路原理及方案
1.1 信号处理电路原理
SAW微力传感器的中心频率是信号处理电路设计所必须的核心参数,一般情况下,叉指换能器(简称IDT)结构和SAW在传感器基片上的传播速度共同决定传感器的中心频率[14],对于本文采用的延迟线型SAW微力传感器,对输入IDT施加一定频率的电信号,通过逆压电效应,传感器基片表面产生SAW,SAW经延迟线传播至输出IDT,最后通过压电效应转换为电信号。
SAW的波长由IDT中叉指的宽度和相邻叉指的间距共同决定[15],表达式为:λ=2(a+b),若SAW在基片材料上的传播速度为Vs,能够得到延迟线型SAW微力传感器的中心频率:
f0=Vs/(a+b)
(1)
微力传感器中SAW的传播特性会受到基片材料物理特性以及外界敏感参数的影响,例如,环境中温度的变化、对基片材料施加微力等等,SAW的传播速度或者幅度、相位则会产生相应的变化。所以需要在SAW微力传感器的基础之上设计信号处理电路对SAW速度或幅度变化的频率进行读取,并对干扰信号进行处理。
通常情况下,设SAW器件的介电常数为ε,环境温度为t,压强为p,基片表面密度为m(m/g2),电导率为σ,弹性参数为c(N/m2),根据表面扰动理论的内容,SAW的传播速度:
Vs=v(m,ε,σ,c,t,p)
(2)
式(2)两边求导后除以Vs可得:
(3)
SAW振荡电路频率与传播速度的关系:
Δf/f0=ΔVs/Vs=
(4)
根据式(4)得到振荡频率的变化量,且可以计算被测参数的值。
1.2 信号处理电路方案选择
微力传感器中SAW的相位、频率、幅度等特性会受到基片材料物理特性以及外界敏感参数的影响,通常情况下可以通过对上述特性变化的检测进而实现对敏感参数的检测[16]。混频法的原理基于频率检测,基于两路传感器及参数一致的SAW振荡电路构成,整体结构如图1所示。
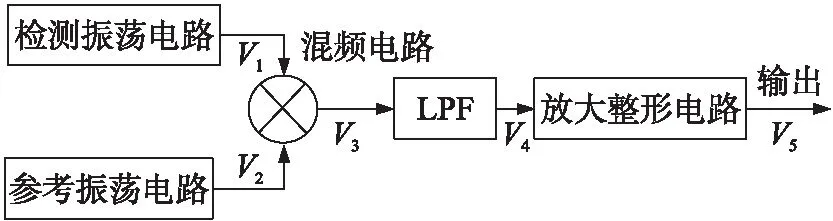
图1 信号处理电路整体结构图
如图1所示,振荡电路作为信号处理电路的信号源,结构上采用检测和参考振荡电路组成双通道,前者检测待测微力,后者用作参考,两个通道输出信号的表达式:
V1=A1cos(ω1t+φ1)
(5)
V2=A2cos(ω2t+φ2)
(6)
式(5)、式(6)中:A1、A2为输出信号幅值;ω1、ω2为输出信号角频率;φ1、φ2为输出信号初始相位。
信号变换电路由混频、滤波和整形电路组成:信号V1和V2通过混频电路后输出信号V3,表达式:
V3=V1×V2=A1A2cos(ω1t+φ1)cos(ω2t+φ2)
(7)
根据三角变换公式,式(7)可表示为:
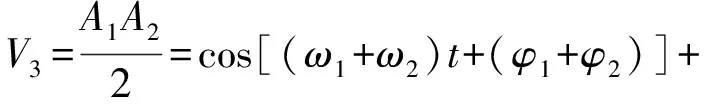
(8)
由式(8)可以看出混频后信号包含ω1+ω2和ω1-ω2的频率信号,需通过低通滤波电路滤除和频ω1+ω2,仅保留差频ω1-ω2信号V4,表达式:
V4=Acos[(ω1-ω2)t]
(9)
式中:A为低通滤波电路输出信号的幅值。
信号V4到逻辑电平V5的转换由整形电路完成。混频检测法中,假设温度等外界因素对基片材料的物理特性产生影响及系统噪声信号引起的干扰导致振荡电路产生的频率变化量为Δω,由于两路振荡电路传感器及参数一致,因此Δω相同,此时,低通滤波电路输出信号表达式为:
V4o=Acos{[(ω1+Δω)-(ω2+Δω)]t}
=Acos[(ω1-ω2)t]
(10)
由式(10)可以看出:经混频电路处理后,输出差频仍为ω1-ω2信号V4,两路Δω被抵消,补偿干扰带来的误差,改善灵敏度和检测精度。
2 声表面波振荡电路
2.1 振荡电路基本原理
振荡电路包括晶体管放大器A和反馈网络F,如图2所示。接通有源器件瞬间的电子噪声首先经过放大器放大,然后由反馈选频网络选出固定频率,反馈到输入端,建立初始振荡[17]。随着振荡幅度不断加大,有源器件产生非线性限制,以形成稳定振荡。
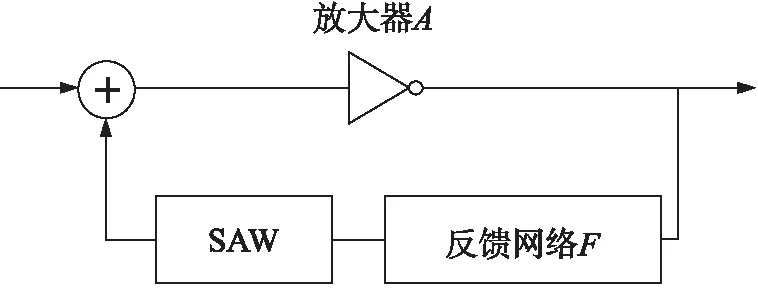
图2 SAW振荡电路结构图
同时,振荡电路正常工作必须满足:
幅值条件:
Ga=Ls+Lp+Lm
(11)
相位条件:
φs+φa+φp=2nπ
(12)
式(11)、式(12)中:Ga为放大器增益,Ls为SAW器件插入损耗,Lp为选频网络插入损耗,Lm为其他部分插入损耗。φs为振荡器相移,φa为放大器相移,φp为选频网络相移。
2.2 SAW微力传感器选型
如图5所示SAW微力传感器部分测试结果,根据上述中心频率与灵敏度关系的分析,本文选取中心频率为49.8 MHZ的延迟线型SAW微力传感器设计振荡电路。

图3 延迟线型SAW微力传感器

图4 网络分析仪连接

图5 传感器测试结果
2.3 SAW振荡电路性能分析
当振荡电路的谐振频率与SAW微力传感器的中心频率相等时,晶体阻抗最小,近似短路,此时电路满足相位与振幅条件,选频网络发生谐振。因此根据SAW微力传感器的中心频率设计振荡频率为49.8 MHz的振荡电路,原理图如6所示。
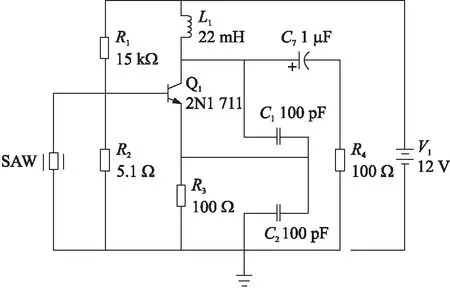
图6 SAW振荡电路原理图
振荡电路的正常起振通过晶体管的谐振放大实现。对于理想的振荡电路,其输出信号:
V0=A0cos(ω0t)
(13)
式中:ω0=2πf0为振荡频率,但在实际工作环境中振荡电路易受到噪声影响,输出:
V0=A(t)cos[ω0t+φ(t)]
(14)
式中:A(t)为调幅噪声,φ(t)为相位噪声,通过式(14)得到实际输出频率:
(15)
式(15)表明随机的相位变化将引起输出信号频率的变化,可得振荡电路的噪声主要是由随机相位的变化而产生的。而对相位噪声的定量分析非常复杂,不但涉及半导体器件的内容,还与采用的分析模型有关,因此具体设计中,选取低噪声的2N1711晶体管降低相位噪声。
图3所示中,R1=15 kΩ、R2=5.1 Ω为基极偏置电阻,R3=100 Ω为控制增益,R4=100 Ω为负载。选频工作由C1、C2、L1完成,其中谐振频率根据SAW传感器的中心频率确定,计算公式:
沥青路面坑槽破损部分经过开槽成型后,其坑槽壁面与坑底表面石料直接裸露在空气中,若直接填入冷补料,将导致冷补料与旧路面材料之间黏结力不足,从而形成壁面缝隙,影响修补路面的抗水损害能力[4]。因此,坑槽在开挖与清扫结束后应喷洒适量的改性乳化沥青作为黏结层,以提高新旧料界面的黏结力。
(16)
然而由于三极管极间电容的存在,且电压源、环境温度等外界因素会使得高频域内振荡频率的稳定性受到影响[19],增大测量误差。为降低这种影响,选频用电容的取值要尽可能大于极间电容的值。但根据SAW振荡电路Leeson相位噪声模型:
(17)
式中:QL为有载品质因数,f0为传感器中心频率,fs为频率偏移量,S1(fs)、S0(fs)分别为、输入、输出相位噪声的功率谱密度。可知振荡频率一定时,若电容值取得过大,那么对应的电感值会变得很小,可能导致该级别电感市场上可选值过少,加上查阅资料得到晶体管2N1711的最大输出电容为25 pF,并结合式(18)得出C1=100 pF,C2=100 pF,L1=1 μH。
3 信号变换电路
低通滤波电路基于Ⅱ型切比雪夫滤波器设计,由于需要通过的信号主要集中在500 kHz以下,所以选用具有高增益带宽的LM6172放大器,其噪声低、转换速率高、失真率低的特点符合设计需求。滤波电路原理图如图7所示。
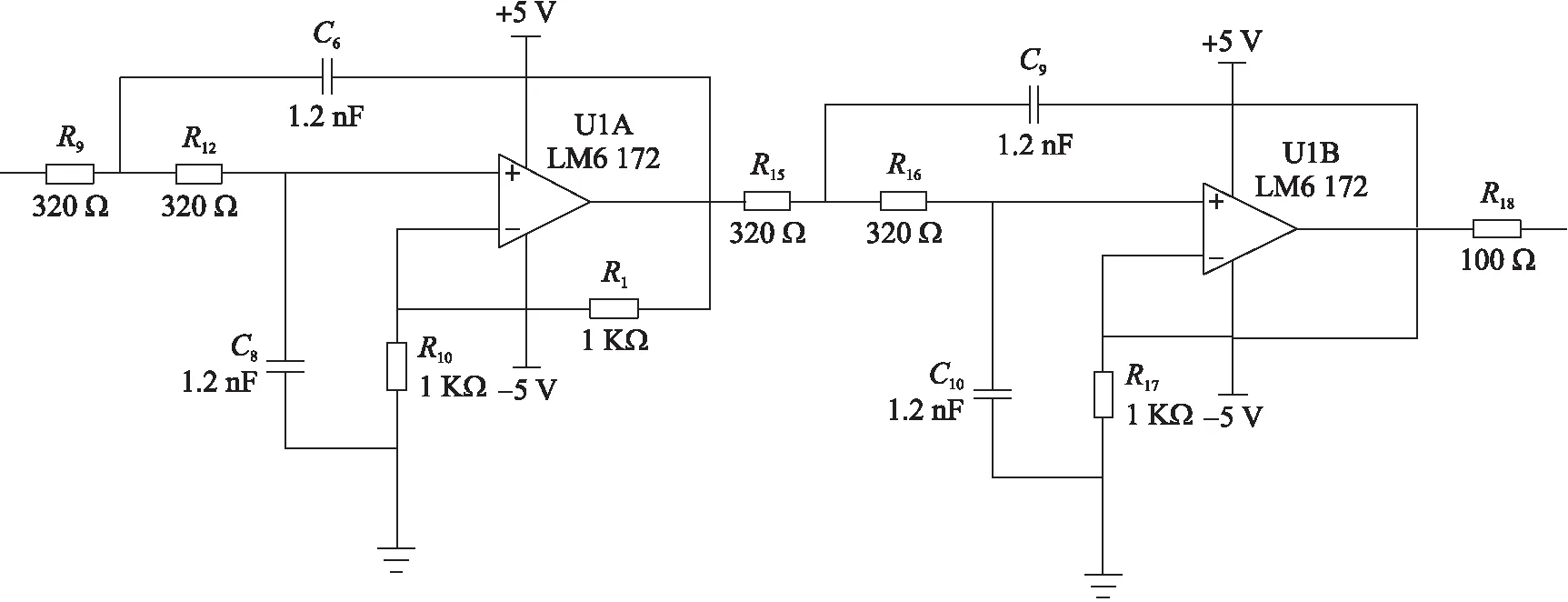
图7 滤波电路原理图
如图7所示采用两级二阶滤波器级联设计完成。以图5中U1A为例,集成运算放大器与R10、R11组成压控电压源,其中运放为同向输入,在运算放大器输出端到同相输入端通过R11引入负反馈,输入阻抗高,输出阻抗低,且性能稳定,增益易调节。其中电阻R9=R12=320 Ω,R10=R11=1 kΩ,电容C6=C8=1.2 nF,U1B中元件参数同理。对滤波电路使用示波器进行测量,测得滤波电路幅频特性,图8所示。
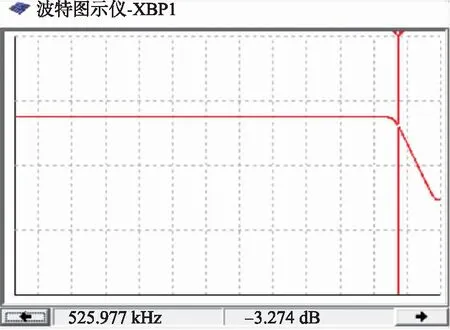
图8 滤波电路幅频特性
由图8可见,低通滤波电路通频带内信号的增益平稳,基本没有纹波,且在输入信号频率达到截止频率时,滤波器的衰减带下降较快,能够将与截止频率相近的信号滤掉,大大减小对后面电路的影响。
整形电路采用LM393芯片组成的电压比较器实现,设置阈值22 mV,根据分压原理可得R13=1 kΩ,R14=250 kΩ,R21=4.7 kΩ为上拉电阻,整形电路原理图如图9所示。
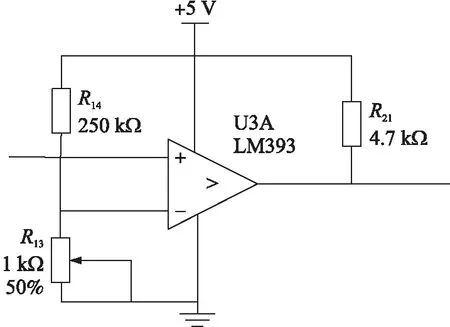
图9 整形电路原理图
4 信号处理电路仿真与分析
系统整体电路图如图10所示,两路振荡电路输出端分别接混频器的两个输入,滤波电路的输入端接混频电路的输出端,由整形电路接收滤波电路的输出信号,至此,完成SAW微力传感器信号调理电路的搭建。
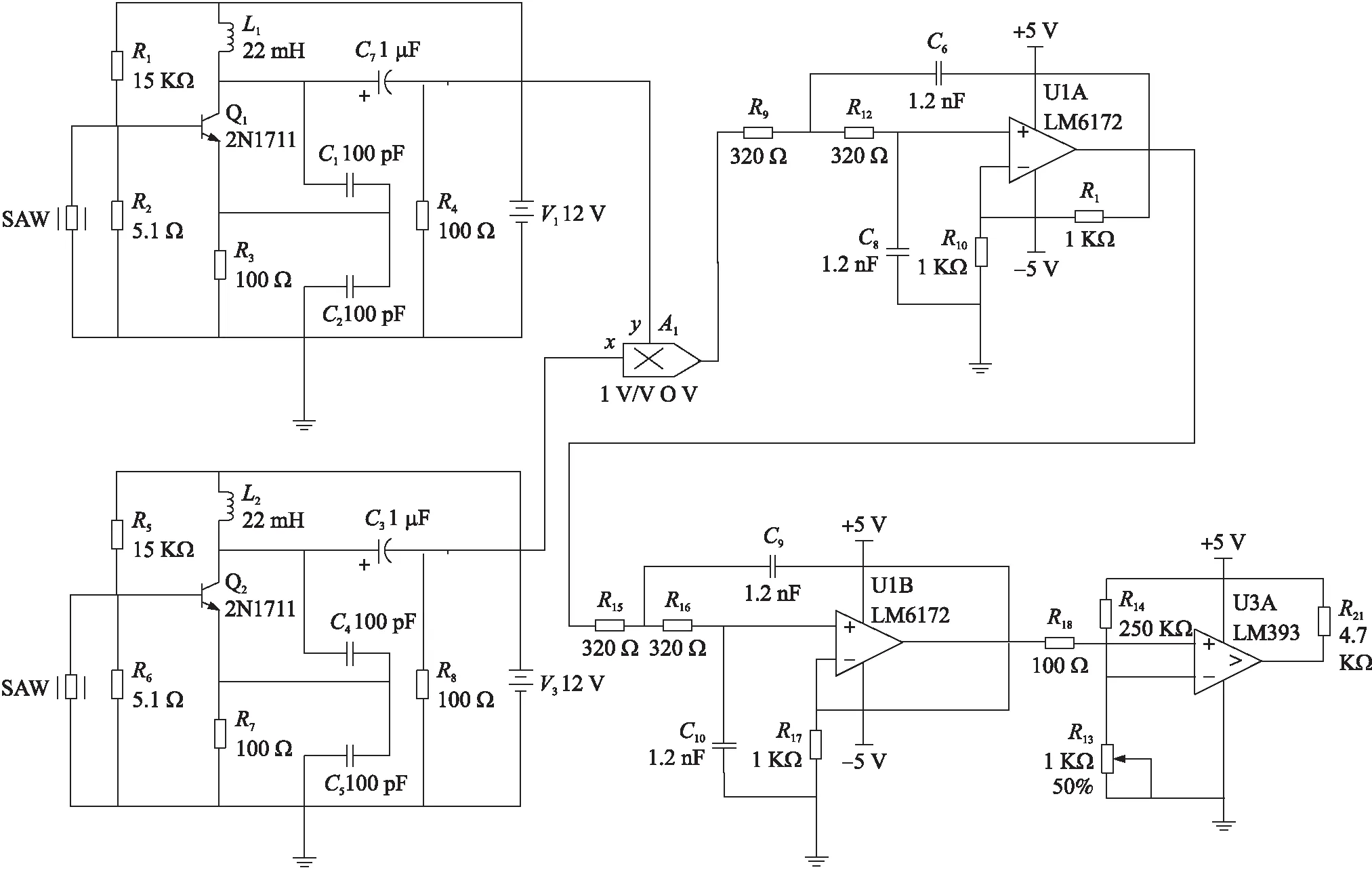
图10 整体电路图
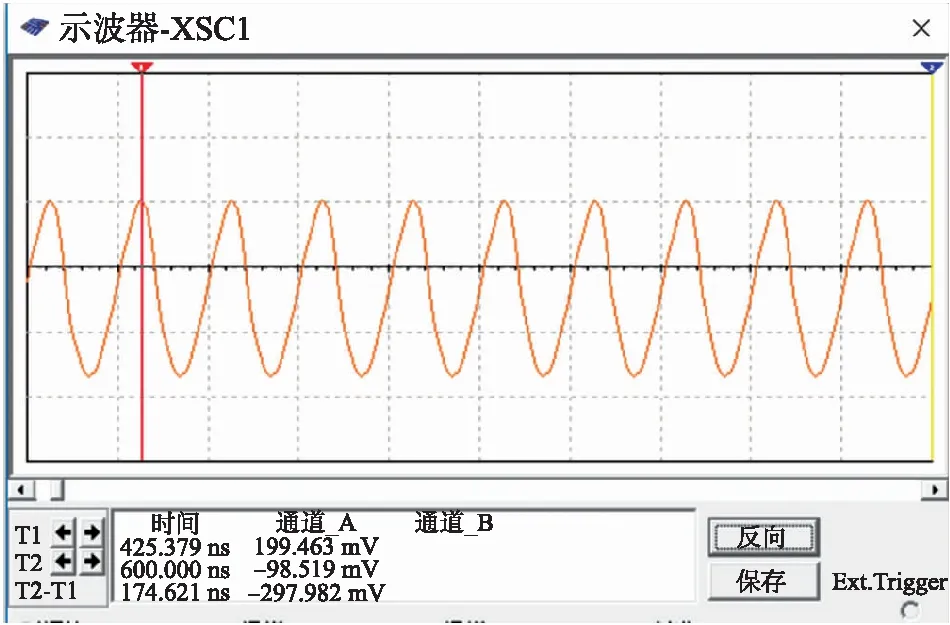
图11 振荡电路输出信号
通过Multisim软件对信号处理电路进行仿真,使用示波器对各模块电路分别进行测试后再对整体电路进行测试。如图11~图14所示分别为振荡电路、混频器、滤波电路和整体电路输出信号仿真波形图。
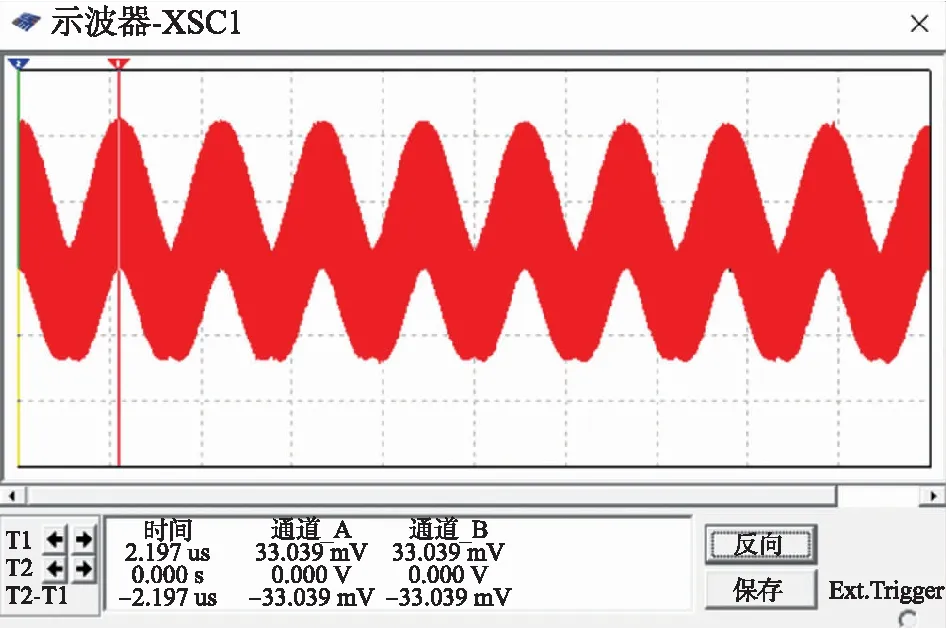
图12 混频器输出信号
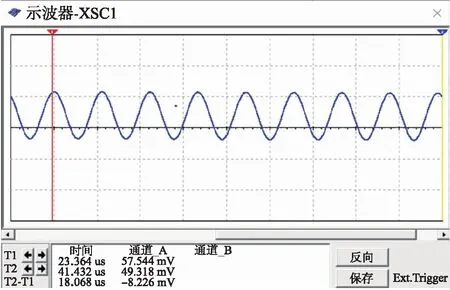
图13 滤波电路输出信号

图14 整体电路输出信号
由图11可见,振荡电路输出信号的频率稳定度较高,虽然与SAW微力传感器的中心频率存在微小差异,但主要关注参数为两路振荡电路混频后的信号,所以误差可以忽略;图12表明混频后稳定输出中频信号,但由于信号中高频噪声干扰的存在,需要低通滤波电路滤除高频噪声,图13中显示信号经滤波电路输出后达到理想的效果,最后在整个电路搭建完成后对其进行仿真得到稳定输出的逻辑电平信号如图14,且电压幅值为5 V,满足一般处理器识别的需求。
5 结束语
本文在SAW微力传感器的基础之上,设计信号处理电路。基于SAW微力传感器搭建振荡电路,解决了SAW振荡电路在高频稳定性、噪声抑制以及灵敏度等方面问题;选取混频检测法为测量方案,稳定输出中频信号,实现将两路SAW振荡电路的差频信号作为待测信号、克服了因单路SAW振荡电路输出的高频信号导致测频困难的问题;设计具有平稳增益、衰减带下降快的滤波电路滤除高频噪声干扰,并搭建整形电路保证输出信号可供一般处理器识别,从而在实际中更容易对敏感参数进行测量。加上在高频稳定性、灵敏度等方面的优势,对SAW微力传感器的发展、应用领域的开拓有着一定的帮助。

