等强度梁式压电振动能量收集器特性研究*

刘延彬(安徽理工大学力学与光电物理学院,安徽 淮南 232001)

近年来,随着集成电路的发展,微机电系统的功耗急剧下降,采用化学电池供能限制了微机电系统几何尺寸的微小型化[1],因此,如何实现从环境中采集能源为低功耗的微机电系统长时间的供能已成为人们亟待解决的问题。振动能量源普遍存在于自然及工业环境中,例如:风激振动、车辆振动、桥梁振动、工程机械工作所产生的振动等,且振动具有较高的能量密度,所以,振动能量收集吸引了更多的研究[2-10]。

根据转换机理的不同,振动能量收集器可以分为压电式[11]、电磁式[12]和静电式[13]、压电-电磁耦合式[14]四类。因为结构简单、易于制作、能量密度高、产生热量小、无电磁干扰、可以实现小型化和集成化,与MEMS技术工艺兼容性好等优点,压电式振动能收集器的研究成为国际上的一个研究热点[1-12]。传统的压电能量收集器的设计原理是基于线性振动力学的共振理论,比较典型的机械结构为悬臂梁结构[15]、圆盘结构[16]和Cymbal结构[17]等。悬臂梁式振动能量收集器的机械结构简单,共振频率可调,在给定外部环境激励条件下具有较大的应变,尤其在低频环境中易于产生共振从而可以采集更多的能量,因此被研究者广泛使用。Sodano等人[18]设计了一种双晶压电悬臂梁式振动能量收集器,该振动能量收集器的优点是通过调整结构尺寸使系统的主频同步于外界振源频率;缺点是结构尺寸较大、能量的转化效率低。Leland 和 Wright[19]设计了一种可调节频率的悬臂梁式振动能量收集器,通过对悬臂梁施加轴向应力改变其刚度,从而改变共振频率,拓宽了其工作频带。Hui-Cong Liu等人[20]基于压电悬臂梁设计了一款阵列式振动能量收集器,其中不同的压电悬臂梁具有不同的共振频率。Ming Song等人[21]采用固定的阻碍物来限制能量收集器质量块的振动幅度,从而扩展了能量收集器的工作频带。Park J C等人[22]采用不对称质量块采集压电悬臂梁不同方向上的振动能量,该振动能量收集器可以收集平面内任意方向的振动能量。

目前,大部分的悬臂梁式压电振动能量收集器均采用等截面梁设计,其抗弯截面系数为常数,但悬臂梁上各截面上的弯矩随着截面的位置而变化。对于等截面压电悬臂梁,不同位置截面上的最大正应力不同,在弯矩为最大值的截面上,截面的最大弯曲正应力才最大,其余各截面上弯矩较小,截面的最大弯曲正应力也就较低,压电材料没有物尽其用;而且,等截面悬臂梁的刚度较大。为了提高压电材料的利用率,降低悬臂梁的刚度,本文采用等强度梁设计方案,在弯矩较大处采用较大的截面,在弯矩较小处采用较小截面,且使各个截面上的最大正应力基本一致,从而提高压电材料的利用率,进而提高能量收集器的能量密度。该方法是文献未曾报导过的,且具有一定的实际应用价值。

图1 微型等强度梁式压电能量收集器示意图

1 振动能量收集器的等强度梁截面宽度

等强度梁不同于等截面梁,其截面尺寸是变化的,故需要给出等强度梁截面尺寸的变化规律。微型等强度梁式压电振动能量收集器的结构如图1所示,其由等强度梁、等截面梁与质量块组成,等强度梁是压电能量收集器的主要工作段,等截面梁联结质量块与变截面梁,质量块起到调剂系统共振频率的作用,其等效力学模型为受集中载荷的悬臂梁如图2所示。其中,b(x)为宽度函数,h为截面高度。

图2 微型等强度梁式振动能量收集器的静力学等效模型

由于微型压电式振动能量收集器的质量块的质量远大于悬臂梁的质量,故建模过程中忽略悬臂梁的质量,且质量块的质量为m,其中

P=mg

(1)

则微型等强度悬臂梁的弯矩方程为:

M(x)=P(l-x)

(2)

由材料力学可知,截面最大应力σ为:

(3)

对于矩形横截面梁,其对Z轴的截面惯性矩为:

(4)

微型等强度梁的固定端宽度为a,则固定端截面的惯性矩为:

(5)

由于微型等强度梁的表面最大应力处处相等,则:

(6)

将式(2)、式(4)和式(5)代入式(6)可得:

(7)

式(7)即为微型等强度悬臂梁的横截面的宽度变化规律。

2 微型等强度梁式振动能量收集器的特性分析

本文采用有限元方法对微型等强度梁式压电振动能量收集器的力学及机电耦合特性进行分析,压电材料选用PZT5,基底选用铝合金,且双层PZT5的输出采用并联形式。计算参数如表1所示。

表1 微型等强度梁式压电振动能量收集器几何参数

2.1 力学特性分析

本部分的计算参数均采用表1的参数,且等截面梁联接的质量块与等强度梁联接的质量块的参数是一样的。

压电层厚度为0.01 mm时,微型等强度梁式压电振动能量收集器静态分析时的应力分布图如图3所示,传统等截面压电振动能量收集器分析时的应力分布图如图4所示。从图3可以看出微型等强度梁的表面应力分布基本相同,在变截面梁的固定端及变截面梁与等截面梁联结部位有应力集中现象,且变截面梁根部的边缘表面应力较小。从图4中可以看出,等截面式振动能量收集器的表面应力差距较大,等截面梁的固定端处表面应力最大,随着距离的增加,表面应力逐渐减小,压电材料并没有物尽其用。对比图3与图4可以明显看出微型等强度式能量收集器的变截面梁表面最大应力为6.22 MPa,等截面能量收集器的表面最大应力为6.04 MPa,微型等强度梁式压电振动能量收集器的压电材料利用率高于等截面式压电振动能量收集器。

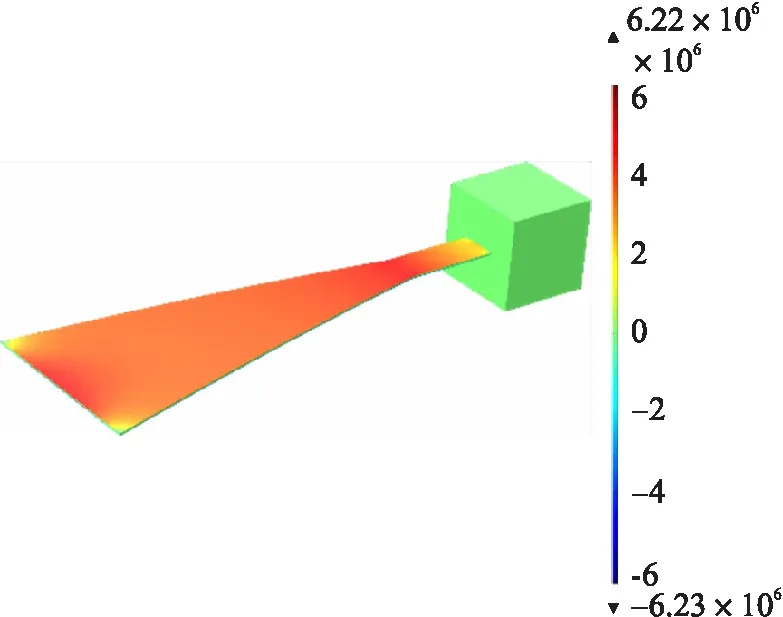
图3 微型等强度梁的表面应力分布图

图4 等截面梁的表面应力分布图

当压电层厚度不同时,微型等强度能量收集器与等截面式能量收集器的一阶固有频率对比图如图5 所示,从图5可以看出微型等强度梁式振动能量收集器的一阶固有频率明显低于等截面梁式振动能量收集器一阶固有频率;且基础层厚度不变的情况下,微型等强度梁与等截面梁式振动能量收集器的一阶频率均随压电层厚度增加而增加,压电层厚度对振动能量收集器的一阶频率影响较大。压电层厚度0.01 mm时,微型等强度梁式压电振动能量收集器的一阶模态图如图6所示,从图6可以看出,其一阶振型为上下振动。压电层厚度0.02 mm时,微型等强度梁式振动能量收集器的质量块中心点随外激励的加速度幅值不同时的振动幅频曲线如图7所示。从图7可以看出,随着外激励加速度的幅值增加,质量块的振动响应的幅值亦增大。

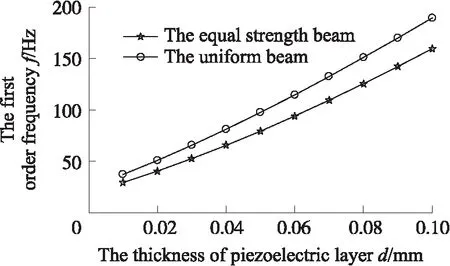
图5 一阶频率-压电层厚度变化曲线对比图

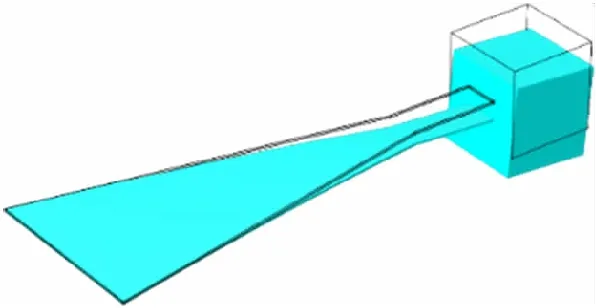
图6 等强度梁式能量收集器的一阶模态

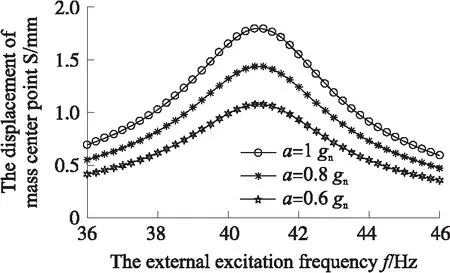
图7 质量块中心点振动的幅-频特性曲线图

图8 电压-位移关系曲线

2.2 机-电耦合特性分析

压电层厚度0.02 mm时,微型等强度梁式压电振动能量收集器的输出电压与质量块中心点的位移关系如图8所示,从图8可以看出,随着位移的增大,其输出电压亦增大,且电压与质量块中心点的位移基本上符合线性关系。

基础层厚度不变,微型等强度梁式压电振动能量收集器无外接负载时,不同压电层厚度的输出电压与频率的关系如图9所示,能量密度如图10所示。

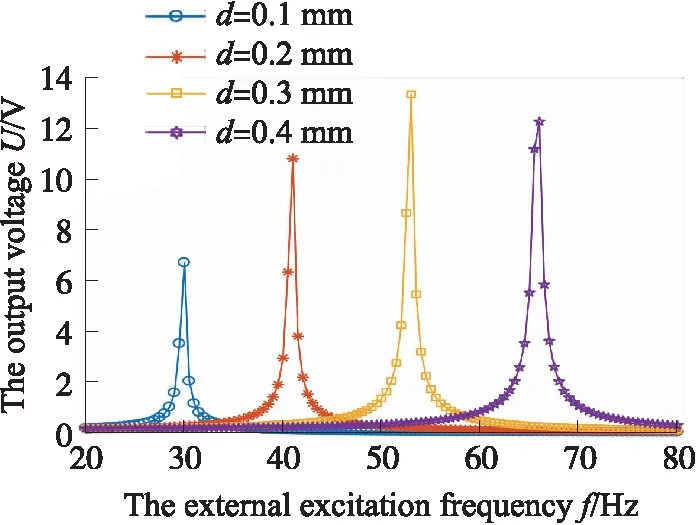
图9 不同压电层厚度的电压-频率曲线

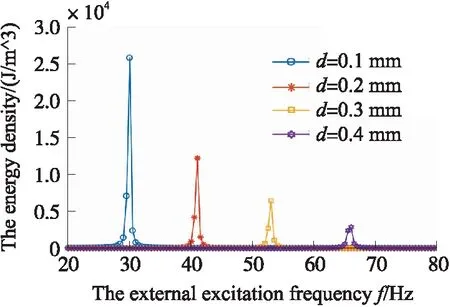
图10 不同压电层厚度的能量密度-频率曲线

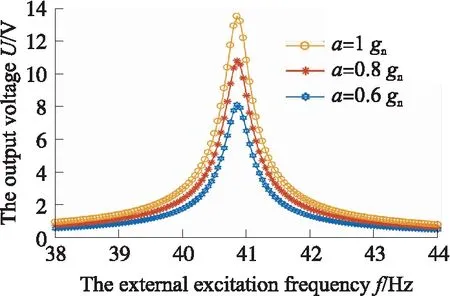
图11 不同加速度的输出电压-频率曲线

从图9可以看出,输出的最大电压随压电材料的厚度增加是先增大后减小的;且随着压电材料的厚度增加,能量收集器的共振频率增加;从图10中可以看出,微型等强度梁式压电振动能量收集器的能量密度随着压电层的厚度增加而减小。压电材料厚度0.02 mm时,微型等强度梁式压电振动能量收集器的输出电压随外激励的加速度幅值不同时的变化曲线如图11所示。

从图11可以看出,随着外激励加速度的幅值增加,微型等强度梁式压电振动能量收集器的输出电压幅值亦增大。压电层厚度0.02 mm,加速度为0.8gn时,微型等强度梁式压电振动能量收集器的输出功率随外接负载变化的曲线如图12所示,从图12可以看出,随着外界负载的增加,微型等强度梁式压电振动能量收集器的输出功率逐渐减小。

微型等强度梁式振动能量收集器与等截面梁式振动能量收集器的电压输出特性对比图如图13所示;外接负载为0.5千欧时,压电材料的能量密度对比图如图13所示。

图13中,微型等强度梁的压电材料体积为5.2 mm3,表面积为522.5 mm2;等截面梁的压电材料体积为10 mm3,表面积为1 003 mm2,等截面梁的表面积及体积均接近于等强梁的表面积及体积的二倍。从图13可以看出,等强度梁的最大输出电压为13.19 V,等截面梁输出的最大电压为22.09 V;由于等截面梁的体积的几乎为等强度梁压电材料体积的2倍,所以等截面梁的输出电压大于等强度梁的输出电压;等强度梁单位体积输出电压2.54 V/mm3,等截面梁的单位体积输出电压为2.209 V/mm3。从图14可以看出,微型等强度梁的压电层的能量密度远大于等截面梁的能量密度。从单位体积输出电压及能量密度角度,等强度梁式压电能量收集器的性能优于等截面梁式压电能量收集器。

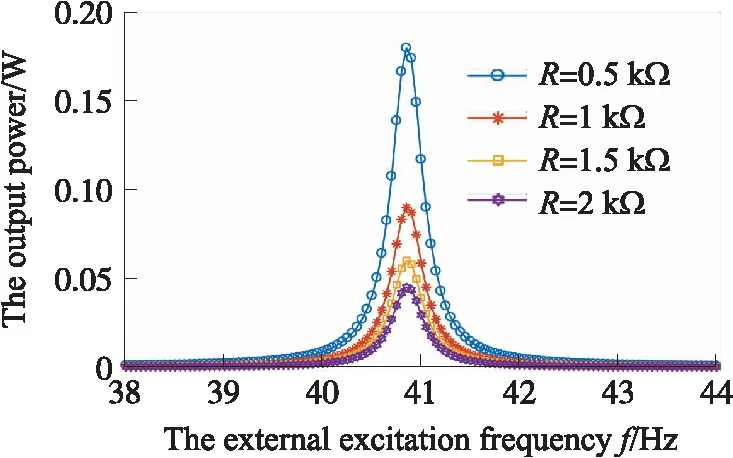
图12 不同外接负载的输出功率-频率曲线图

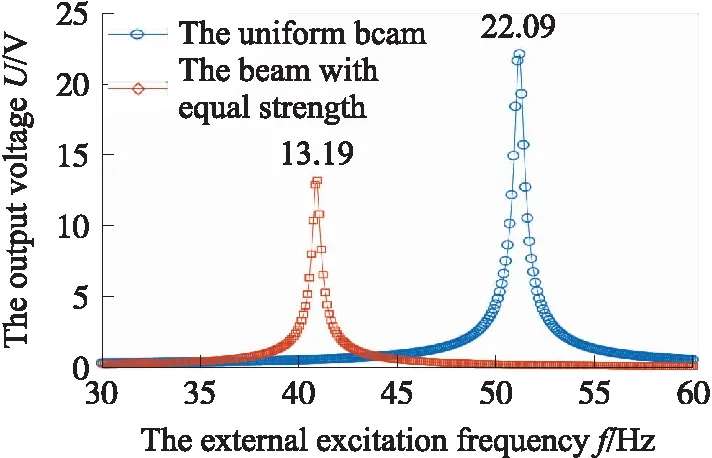
图13 输出电压对比

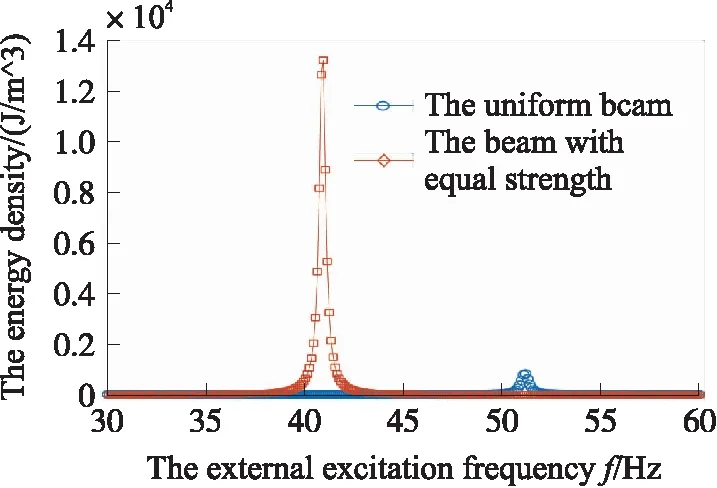
图14 输出能量密度对

3 结论

基于等强度梁理论设计了一种微型压电式振动能量收集器,对其力学及机电耦合特性进行了系统研究,并且与传统的等截面悬臂梁式压电振动能量收集器进行了对比,得到以下几点结论:

①与传统的等截面悬臂梁式压电振动能量收集器相比,微型等强度悬臂梁式压电振动能量收集器具有固有频率低、表面应力分布合理、压电材料利用率高、能量输出密度大等优点。

②基础层厚度不变的情况下,微型等强度悬臂梁式压电振动能量收集器的一阶固有频率随压电层厚度增加而增加,输出的最大电压随压电层的厚度增加是先增大后减小。

③微型等强度梁式压电振动能量收集器的输出功率随外接负载的增加而逐渐减小。

④从单位体积输出电压及能量密度角度,等强度梁式压电能量收集器的性能优于等截面梁式压电能量收集器。