数控机床爬行的模糊PI控制研究**
尹 明 晁佳佳
(内蒙古科技大学机械工程学院,内蒙古包头014010)
随着制造业的迅速发展,高产量高精度数控机床的需求日益迫切。机床在低速重载的工况下,时常会发生忽停忽动忽快忽慢的非正常工作状态,称之为爬行又叫作粘滑运动。一旦出现爬行,机械传动变得不均匀,伺服系统无法实现精确的测量和定位,极大地影响着工件加工质量。目前国内外研究人员针对爬行现象开展了大量研究,在一定程度上揭示了爬行发生的机理,提出了一些解决方法。AK Banerjee[1]认为爬行是非线性摩擦力引起的自激振动现象。B Armstrong[2]等在机器人系统中加入脉冲信号,有效地消除了爬行现象。Karl Popp[3]等设计了被动爬行控制系统,并通过计算证实了该方法的可行性。目前关于爬行抑制方法研究取得了一定的成果,但是并没有在根本上完全消除爬行现象。本文开发了一种基于超磁致伸缩致动器(GMA)的爬行控制系统,模糊PI控制器根据相关算法驱动GMA产生相应的输出力抑制机床爬行。通过软件仿真证明了该系统对数控机床爬行具有良好的控制作用。
1 爬行控制系统的整体设计
超磁致伸缩材料Terfenol-D作为一种新型的智能材料,其长度和体积会随着磁化状态的变化而变化。超磁致伸缩致动器正是根据这一特性,实现电磁能和机械能的转化。超磁致伸缩致动器具有应变大,响应快,能量转化率高等优势,因此被选用作为外加激励发生器[4]。
基于超磁致伸缩致动器的激励系统如图1所示,滚珠丝杠螺母副丝杠采用一段固定一段浮动的支撑方式,致动器的输出杆与丝杠浮动端刚性固连,在激励磁场的作用下,对丝杠进行拉伸和压缩。由于丝杠形变量较小,忽略丝杠形变后传动比的变化。
当数控机床在工作过程中产生爬行时,通过传感器对工作台的速度进行测量,将测得数据输入到模糊PI控制器中[5],再根据已经编写好的控制算法,给出适当的驱动电流驱动GMA产生一定的输出力,通过丝杠传递给工作台,抑制工作台的不稳定运动,以达到消除爬行的效果。

2 爬行控制系统模型的建立
2.1 GMA的数学模型
为了方便系统动力学建模,作如下简化:致动器壳体、底座、输出杆以及轴承为刚体,在工作过程中不发生变形;Terfenol-D棒输出端、输出杆和丝杠左端的连接没有缝隙,三者的位移、速度和加速度相同;忽略预压机构的阻尼和刚度;将丝杠看作刚度为Kl、阻尼为Cl的弹簧阻尼结构,Ml代表丝杠和工作台的等效质量;Ke和Ce为GMA棒在形变过程中所要克服的自身的等效刚度和等效阻尼;Me为GMA棒和输出杆的等效质量。建立超磁致伸缩致动器激励系统力学模型如图 2 所示[6]。
为了对超磁致伸缩效应加以应用,使用能量守恒定律、克希荷夫定律等已知的物理定律建立超磁致伸缩致动器动态力学模型,求出其运动方程。在建模之前我们做出以下假设:(1)忽略涡流效应以及漏磁现象的影响。(2)Terfenol-D棒的各项参数不随环境改变而变动,看作定值计算。(3)工作中Terfenol-D棒的伸缩长度随磁场强度线性变化[7]。

式中:N为线圈匝数;i为线圈中驱动电流;x为致动器输出位移;d33为GMA棒的轴向动态伸缩系数。求解出致动器磁路磁通为:
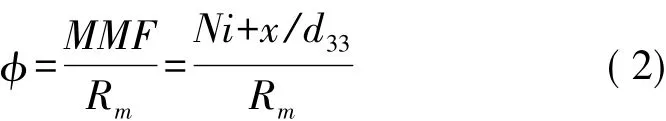

致动器等效磁路的磁动势MMF为:
式中:Rm为致动器总磁阻。得到致动器的输出力F为:


分析致动器受力状况,求得平衡方程为:
式中:M=Me+Ml,C=Ce+Cl,K=Ke+Kl。
令固有频率ωn=槡K/M,系统阻尼比ζ=C/2Mωn。对式(4)做Laplace运算处理得:

综合公式(1)~(5)可以得到超磁致伸缩致动器的传递函数为:
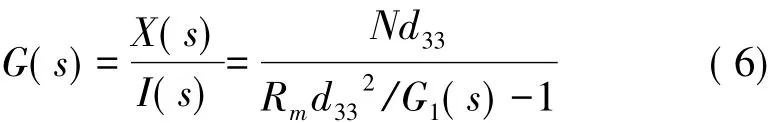
2.2 数控机床爬行的简单物理模型
数控机床的进给系统主要由驱动装置、机械传动机构以及被驱动件构成。伺服电动机接受数控系统发出的指令开始工作,动力经过联轴器、齿轮副、丝杠螺母副的传递后,最终将伺服电动机的旋转运动转换为工作台的直线运动。爬行主要发生在数控机床进给系统的被驱动件上,即工作台和刀架等。传动系统刚度不足和运动过程中导轨摩擦力的变化被认为是引起爬行的主要原因。
为了方便研究,我们假设齿轮副和丝杠螺母副的摩擦系数远小于导轨摩擦系数,忽略不计;工作台在垂直方向不发生移动且进给系统中没有传动间隙。并建立如图3所示的进给系统运动简单物理模型。简化进给系统结构,不仅有利于建立工作台运动方程也给爬行现象动态仿真带来极大的便利[8]。
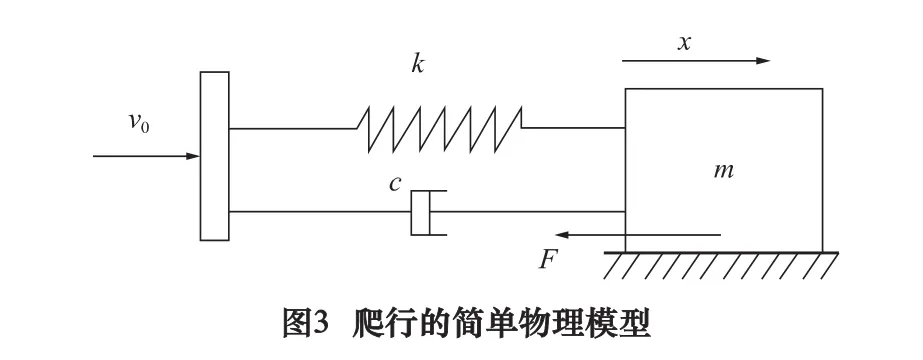
图3将数控机床进给系统简化成一个以恒定速度v0驱动、摩擦阻力为F的单自由度运动系统。应用集中参数离散化的原理把工作台抽象成一个质量为m的质块,把机械传动机构看成一个无质量的弹簧阻尼结构。k和c分别代表传动机构的传动刚度和传动阻尼系数。
2.3 ADAMS与MATLAB联合仿真系统的建立
为了研究基于超磁致伸缩致动器的控制系统对爬行的抑制效果,需要结合Adams和Matlab进行联合仿真分析。联合仿真的实现主要可以分为3个步骤:(1)通过Adams软件建立爬行简单物理模型,定义各部件参数和约束关系。设置仿真参数,建立系统控制变量输入以及运动参数输出端口。(2)使用Matlab/Simulink建立超磁致伸缩致动器激励系统动态力学模型。(3)将致动器力输出与ADAMS输入端口相连接,定义超磁致伸缩致动器工作电流,设置仿真条件开展联合仿真。ADAMS是当前最为流行的机械系统运动学仿真软件,而Matlab具有强大的计算与模块化建模能力。联合仿真能够充分发挥两个软件各自的优势,更准确地表现出机械电子系统在工作中的实际状况。

表1 进给系统运动仿真参数表
为了实现Adams与Matlab之间数据的传递与结果的输出,在Adams中分别建立工作台水平方向力激励,工作台速度两个变量端口,并根据表1中数据对各模块参数进行设置。建立进给系统运动仿真模型机械子系统如图4所示。
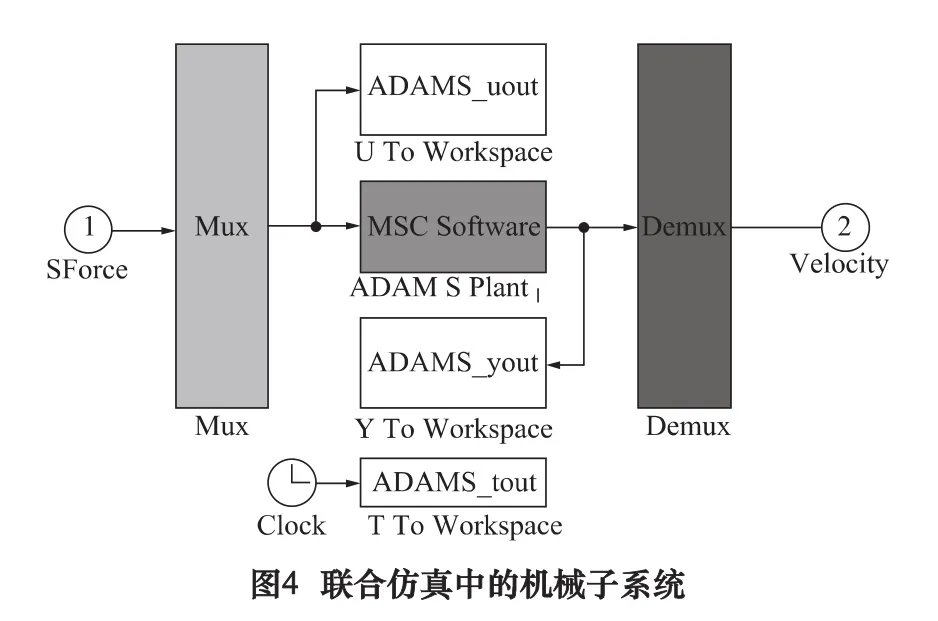
假设螺母和丝杠刚性接触,工作台初始工作位置在丝杠最左侧。丝杠长500 mm,驱动速度4 mm/s,由于仿真时间短速度小,忽略仿真过程中工作台位移的变化,工作台运动过程中受到的激励与丝杠致动器顶端近似相等。根据公式(6)可以求出在GMA的激励下,工作台位移、速度、加速度的变化值。根据图3,已知伺服系统传动机构阻尼、刚度和工作台质量,可求出在超磁致伸缩致动器的作用下,工作台受到的等效激励力。将上述关系封装为以磁致伸缩位移x为输入,等效激励力Fe为输出的子系统。将Adams爬行运动机械子系统通过Adams/Control模块导入到Matlab/Simulink中,作为其中的一个子模块。致动器传递函数框图和机械子系统相连接,得到基于超磁致伸缩致动器激励系统模型如图5所示[9]。
3 爬行控制系统的模糊PI控制器设计
设计的自适应模糊PI控制器以常规PI控制系统为基础,采用模糊推理思想,控制量的偏差e和偏差变化率ec作为模糊控制器的输入,PI控制器的变化量作为输出,利用模糊控制规律在线整定PID控制器各项参数[10]。与常规PI控制相比,具有良好的动、静态性能。KP、KI的调整公式为:
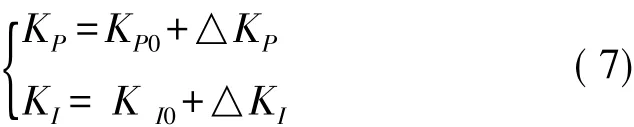
式中:KP0、KI0是 KP、KI的初始参数由试凑法得出;ΔKP和ΔKI是利用模糊关系根据e、ec计算出的调整值。

根据系统实际情况,方便计算。将输入参数c和输出参数的模糊论域都取为[-6,6]。为了使控制器具有良好的精度和响应速度,输入输出变量的模糊子集都采用{负大负中负小零正小正中正大}来表示,简记为{NB NM NS ZO PS PM PB}。由于三角形函数分辨率高且控制灵敏,因此将其选为系统的隶属度函数,输入输出变量的模糊隶属度函数如图6所示。

根据PID控制原理可以知道,比例环节P可以快速地按比例消除偏差。积分环节I用来消除静差,提高系统的无差度。而微分环节D能够预测误差变化趋势,提前做出调整。由于本系统偏差变化率较大,微分控制会导致系统的不稳定,因此只采用PI控制[11]。
根据各项控制参数对控制系统影响特性,得出针对不同偏差和偏差变化率时,参数的自整定原则。
(1)当误差e较大时,无论误差变化率ec的值如何,为了使系统快速稳定下来应该取较大的KP。为了避免系统超调,KI的值应该取得小一些。
(2)当e和ec为中等大小时,为了减小系统超调,应取较小的KP。适当的增大KI的值以保证系统的响应速度。
(3)当误差e较小时,取较大的KP和KI,以避免系统出现稳态误差。
根据上述关系,得到模糊PID控制器KP、KI的调节规则表,如表2、3所示。
4 爬行的模糊PI控制系统仿真
基于以上分析,使用Matlab/Simulink建立爬行的模糊PI控制系统模型如图7所示。图中g1和g2分别表示模糊逻辑控制器P控制和I控制输出参数的比例因子;Ke和Kec分别代表误差和误差变化率的量化因子;KP0和KI0分别代表P控制和I控制的初始参数。根据经验和大量调试,设PI控制参数的初始值KP0=2,KI0=5。


表2 ΔKp模糊规则表

表3 ΔKI模糊规则表
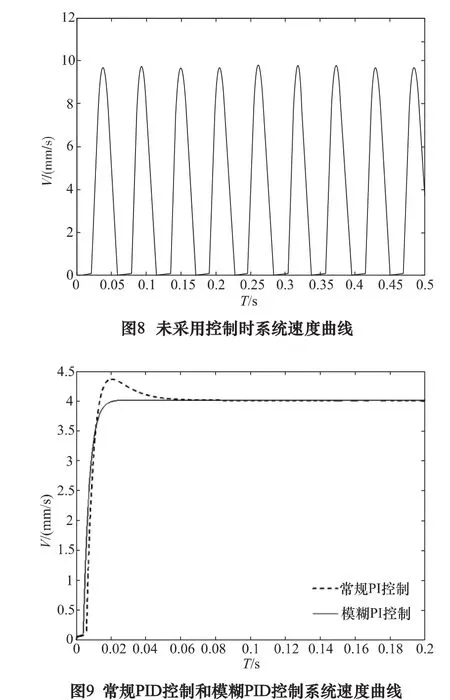
当系统没有采用控制的时候,系统运动速度曲线如图8所示。速度波动大且有零点,运动发生停滞,系统出现爬行现象。
分别使用常规PI控制和模糊PI控制时,系统运动曲线如图9所示。在引入PI控制后,爬行现象消失,系统运动稳定性有了很大的改善,很快达到驱动速度并稳定。此外模糊PI控制要明显优于常规PI控制,模糊PI控制能够实现PI控制参数的在线调整,系统速度曲线没有出现超调,过渡时间大大缩短,系统表现出良好的稳定性。
5 结语
设计了以超磁致伸缩致动器为执行器的模糊PI控制系统,通过Adams和Simulink建立控制系统联合仿真模型。借助Matlab/Fuzzy工具箱设计了模糊PI控制算法对控制系统进行控制。系统仿真结果表明,PI控制有效地消除了数控机床工作过程中的爬行现象。模糊PI控制能够对控制参数进行实时调整,与常规PI控制相比超调消失,调整时间缩短至0.02 s,控制效果更好。使用模糊PI控制对数控机床爬行进行控制,取得满意的控制效果,可以在实际设计生产中进行推广。

