“建桥合一”铁路客站Rayleigh阻尼系数计算方法

徐汉勇， 李玲瑶， 余志武

(1. 长沙学院 土木工程学院， 湖南 长沙 410022； 2. 中南大学 高速铁路建造技术国家工程实验室， 湖南 长沙 410083)

“建桥合一”铁路客站集轨道层、高架候车层和屋盖层于一体，设有单独与铁路、地铁、出租车和公交车辆相连的通道，旅客在换乘时可采用“零距离”的方式，满足原铁道部对新建铁路客站“功能性、系统性、先进性、文化性、经济性”的五项要求。因此，广泛应用于实际工程中，如新广州站[1]、北京南站[2]、天津西站[3]、上海虹桥站[4]等。

为便于车流、客流和候车，采用“建桥合一”的结构体系时，一般采用混合结构形式，轨道层和高架候车层采用大跨框架结构、屋盖层采用大跨空间钢结构[2-4]。为便于采光，屋盖层空间钢结构未设置钢筋混凝土楼板[1-4]，相同标高节点的同向水平位移缺少楼板的刚性约束，致使振型质量参与系数分布离散化，即要使结构各向振型质量参与系数累计数满足文献[5]要求，需要提取多阶振型，表明多阶振型对结构地震响应的影响显著。因此，在基于振型计算“建桥合一”铁路客站Rayleigh阻尼系数时，需要考虑多阶振型的影响。目前，现有的Rayleigh阻尼系数计算方法主要有两类：第一类是基于二阶参考振型的计算方法[6-7]，该方法只能确保选取的二阶参考振型对结构响应的影响；第二类是基于单维地震激励和多阶参考振型的计算方法，采用SRSS振型组合法建立节点位移或结构层间位移角的变化量与Rayleigh阻尼系数间的关系式，并根据要使响应变化量最小、关系式对阻尼系数的求导等于零的原则，求得阻尼系数[8-11]。文献[12]指出，京沪高铁天津西站Ⅱ区屋盖层的相连杆件既不垂直又非共线，致使构件响应的耦合显著，在抗震计算时，应考虑多维地震激励同时作用，不宜忽略振型相关性和异向地震激励相关性对结构响应的影响。为此，本文结合基于三维随机振动原理的节点位移计算公式、水平向和竖向互功率谱的线性修正表达式、加速度反应谱的规范算法和文献[8-9]的研究成果，提出了能合理考虑异向地震激励相关性和振型相关性，且具有统计意义的Rayleigh阻尼系数计算方法，并以天津西站Ⅱ区为例，进行验证。

1 水平向和竖向互功率谱线性修正表达式

( 1 )

( 2 )

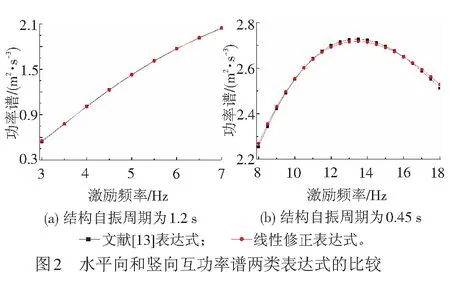
由于水平向和竖向互功率谱的非线性表达式，无法使节点位移响应功率谱的计算式得到简化，致使文献[13]提出的多维实用反应谱法忽略了水平向和竖向互功率谱对结构响应的影响。考虑到影响节点位移的主要影响因素有激励频率、结构自振频率和结构自身阻尼，构建了水平向和竖向互功率谱线性修正表达式的过程为

Step1对结构进行模态分析，提取各振型频率和振型阻尼比，并以此作为结构动力特性构建单自由度体系。

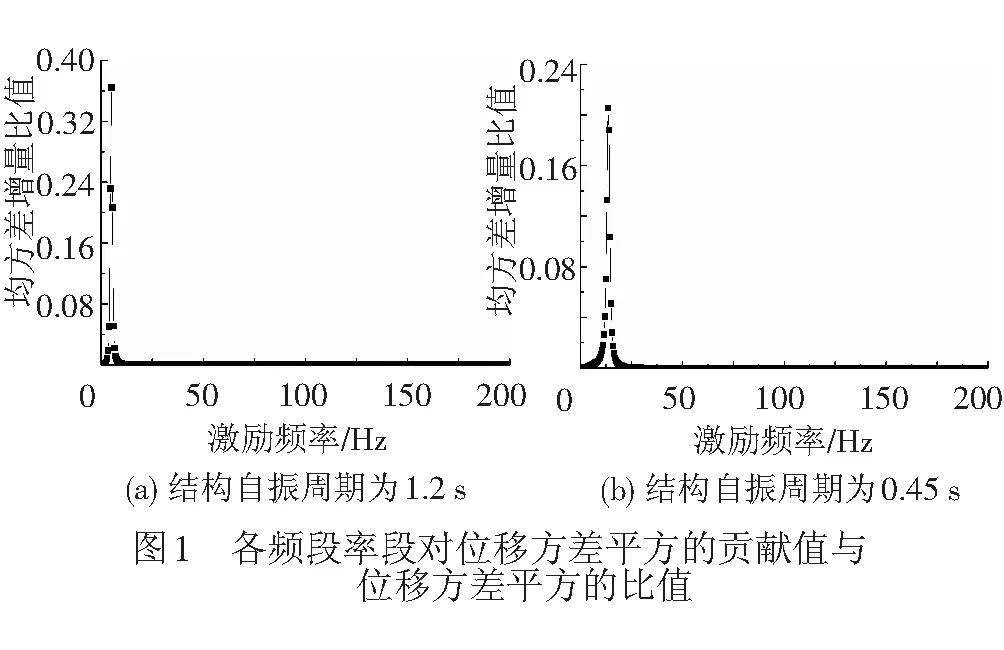
Step2对该单自由度体系施加平稳激励，激励形式采用式( 1 )或式( 2 )，将激励频率分成若干等间隔段，求得各频率间隔段对节点位移方差平方的贡献值、位移方差的平方和两者的比值。

Step3通过比较，得到Step2比值的峰值，以此为参考，确定显著影响该单自由度体系位移响应的激励频率范围，并在该范围内，采用最小二乘法求得水平功率谱和竖向功率谱线性组合的系数，再用该组合代替式( 1 )或式( 2 )。

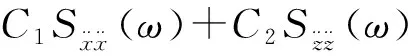
2 三维地震激励节点位移计算公式

利用传统随机振动原理，三维平动地震作用下节点位移的功率谱矩阵为

( 3 )

式中：SUU(ω)为节点位移的功率谱矩阵；rjl、rip为振型参与系数；NM为振型的阶数；Hi为频响函数

其中，ωi和ξi分别为第i阶振型的圆频率和阻尼比；Hj类似；*为共轭；i为虚数单位；φj、φi为振型；Slp为激励功率谱。

将式( 3 )展开，得

( 4 )

rj2ri3C1iA2+rj3ri1C1iA1+rj3ri2C1iA2)·

( 5 )

SUU(ω)的对角线表示节点位移的自功率谱，任取第k项，其值为

A2+rj2ri3C1iA2+rj3ri1C1iA1+rj3·

Ci2+rj3ri1Ci2+rj3ri2C2i+rj3ri3)·

( 6 )

ri3C1iA2+rj3ri1C1iA1+rj3ri2C1iA2)·

(rj1ri3Ci2+rj2ri3Ci2+rj3ri1Ci2+rj3·

( 7 )

根据文献[14]

( 8 )

( 9 )

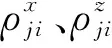
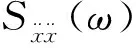
类似σxj，可得σzj和σzi，则三维地震激励节点位移方差为

axi+(rj1ri3Ci2+rj2ri3Ci2+rj3ri1Ci2+

(10)

3 多维激励多阶参考振型Rayleigh阻尼系数计算模式

Rayleigh阻尼模型假设结构阻尼矩阵为结构质量矩阵和刚度矩阵的线性组合，表达式为

C=αM+βK

(11)

式中：α、β是Rayleigh阻尼系数，分别为质量、刚度比例阻尼系数；C、M、K分别为阻尼、质量、刚度矩阵。

采用文献[8-9]给出的节点位移或层间位移变化量与阻尼系数的关系式为

(12)

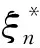
现将式( 8 )变为

(13)

axi+(rj1ri3Ci2+rj2ri3Ci2+rj3ri1Ci2+rj3·

(14)

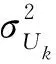
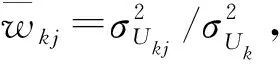
(15)

(16)

可得

(17)

(18)

4 算法验证

4.1 工程概况

天津西站Ⅱ区的轨道层、高架候车层和屋盖层分别采用钢管混凝土柱型钢混凝土梁框架结构、钢管混凝土柱H型钢空间桁架框架结构和联方单层柱面网壳结构，见图3。底层横向7跨，左右对称，跨度为(3.8×2+21×4+24) m，纵向5跨，跨度均为21.5 m；二层横向7跨，纵向5跨，跨度均类同底层，桁架高为2.88 m，桁架下弦与设备层楼板相连，横向上弦与候车厅楼板相连，两端设有工字钢转换梁，并在其两端及中间设置工字型短梁；屋盖层网壳支承在斜柱上，斜柱底端与工字型短梁相连，高为20 m，纵向间距为10.75 m，网壳跨度为105.4 m，矢高比为0.35，拱肋与斜柱均采用箱形钢截面。

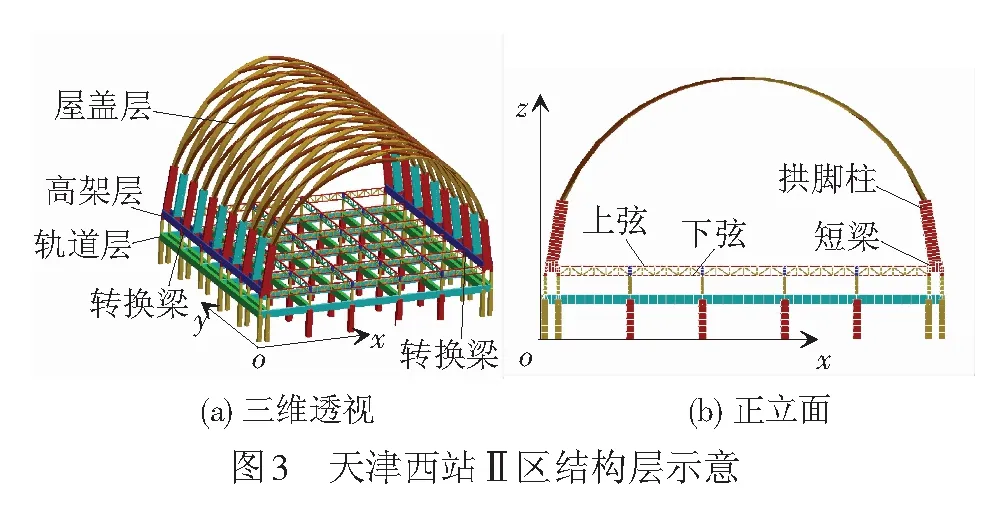
采用ANSYS软件建立有限元模型，梁柱采用beam4单元，楼板采用shell63单元。根据文献[5]，由于轨道层和高架候车层均带钢筋混凝土楼板，钢管混凝土柱、型钢混凝土梁、钢桁架构件的阻尼比取为0.04，而屋盖层空旷钢结构构件的阻尼比为0.02，差异显著。为此，在建立有限元模型时，按照阻尼比的不同，将构件进行归类。

天津西站Ⅱ区前70阶振型的水平x向和y向振型质量参与系数的分布特点见图4。由图4可见，对于x向振型质量参与系数，第1、9、14、15、28、29、44阶显著不为零，对于y向振型质量参与系数，整体结构模型的第2、5、11、13、32阶振型显著不为零。

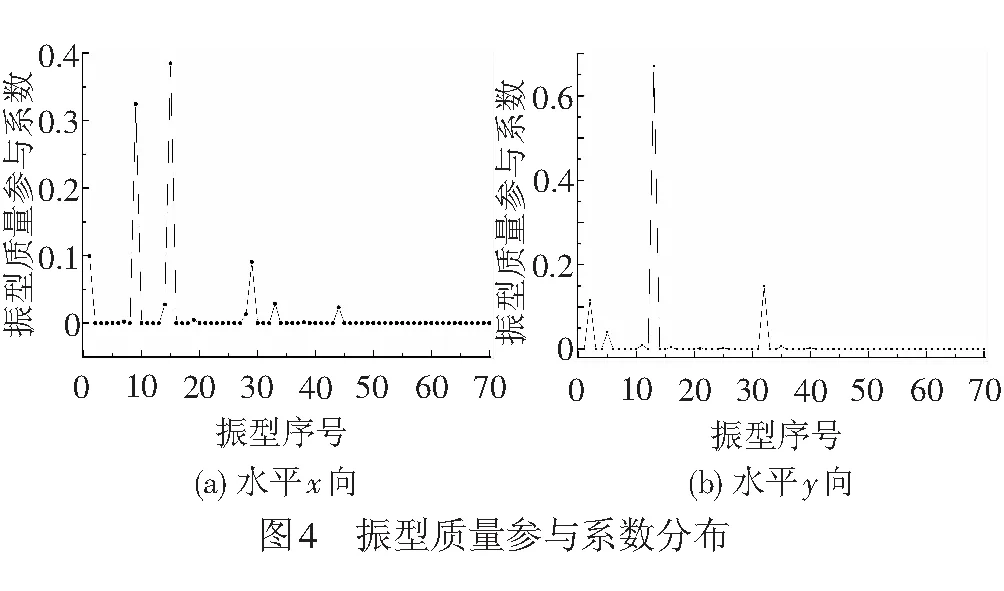
天津西站Ⅱ区场地类别为Ⅲ类，选取了普遍应用的El-Centro地震波。在三维地震激励作用下，对利用应变能振型阻尼模型及二阶、单维激励多阶、多维激励多阶参考振型Rayleigh阻尼系数计算方法的结构时程响应值进行了比较，水平x、y向和竖向地震加速度峰值之比为1∶0.85∶0.65。应注意的是，由于轨道层、高架候车层和屋盖层构件阻尼比差异显著，因此，采用应变能振型阻尼模型进行弹性抗震计算更合理[15]。在结构时程响应值比较时，选择以基于应变能振型阻尼模型求得的时程响应值为标准。对于二阶参考振型阻尼系数计算方法，选取了第1、2阶振型作为参考，阻尼系数α、β分别为0.051 8、0.002 9；对于单维激励多阶参考振型阻尼系数计算方法，阻尼系数α、β分别为0.004 7、0.003 5；对于多维激励多阶参考振型阻尼系数计算方法，A1、A2分别取为1.0、0.852。在确定权重系数时，按照文献[8-9]建议，在考虑多阶振型影响时，宜取最大层间位移或节点位移，本文选取屋盖层x向层间位移，求得的阻尼系数α、β分别为0.140 8、0.003 4。各结构层层间位移角最大值和增量见表1，结构应变能的时程响应见图5，计算方法见文献[12]。由图5、表1可见，相比二阶参考振型和单维激励多阶参考振型阻尼系数计算方法，基于多维激励多阶参考振型阻尼系数计算方法求得响应值的偏差最小，表明更适合于空间相关性强的“建桥合一”铁路客站Rayleigh系数的计算。

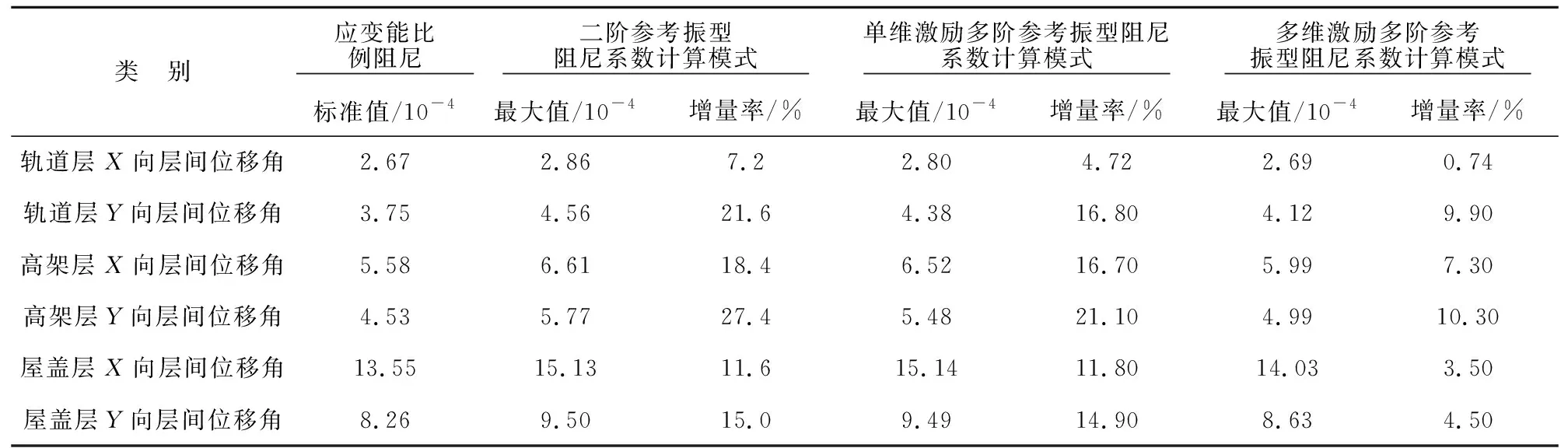
表1 结构层层间位移角最大值和增量率

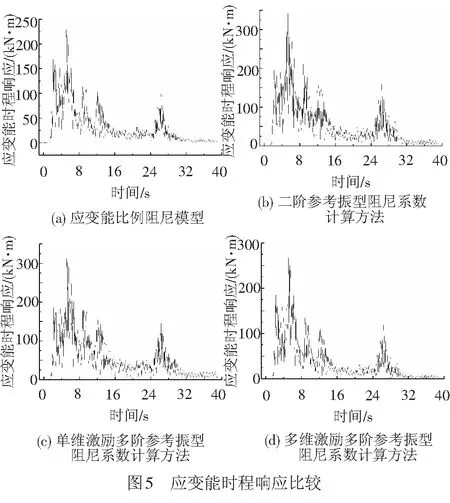
5 结论

本文基于水平向和竖向地震加速度互功率谱的线性修正表达式、传统随机振动计算方法和规范加速度谱提出了多维激励多阶参考振型Rayleigh阻尼系数计算方法，并以“建桥合一”铁路客站天津西站为例，对多类阻尼系数计算方法的结构时程响应值进行了比较，得出以下结论：

(1) 提出了水平向和竖向地震激励加速度互功率谱线性修正表达式的构建方法，能有效地保留显著影响位移响应的激励频率范围，计算误差小，且能很好地简化利用传统随机振动原理得到的节点位移功率谱计算公式。

(2) 提出的多维激励多阶参考振型Rayleigh阻尼系数计算方法能合理考虑地震激励相关性和振型相关性对结构响应的影响。

(3) 相比常用的二阶、单维激励多阶参考振型Rayleigh阻尼系数计算方法，利用多维激励多阶参考振型Rayleigh阻尼系数计算方法求得的“建桥合一”铁路客站天津西站Ⅱ区的响应值更合理。