几类圆周运动临界问题的归类分析

广东 魏志钟

圆周运动问题是高中物理的重点内容，由于圆周运动的基本解题思路相同，让我们常有“似曾相识”的感觉，但圆周运动的临界问题错综复杂，临界条件相对隐蔽，让学生不知从何下手。对于圆周运动模型，按照知识点的综合归类情况，主要分以下三类情形：

一、水平面内圆周运动的临界问题

水平面内圆周运动的临界极值问题通常分两类，一类是与摩擦力有关的临界问题，物体间恰好不发生相对滑动的临界条件是物体间的静摩擦力恰好达到最大值；一类是与弹力有关的临界问题，压力、支持力的临界条件是物体间的弹力恰好为零，绳上拉力的临界条件是绳恰好拉直且其上无弹力或绳上拉力恰好为最大承受力等。

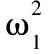
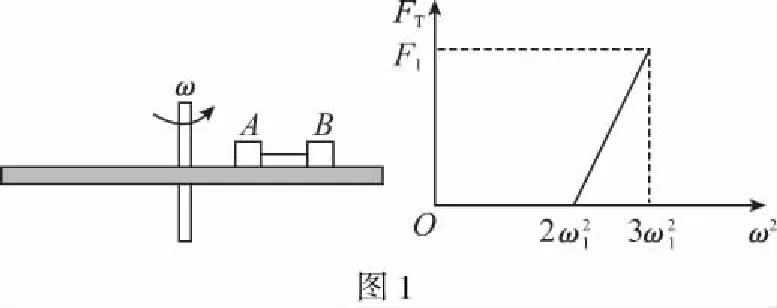
【答案】BC

【动态分析】解题前我们应先构建其运动模型，当ω较小时线O1A拉直，O2A松弛，当细线O1A、O2A都拉直时，随着ω增加，线O1A的拉力逐渐减小、O2A的拉力逐渐增加；而当ω太大时，O2A拉直,O1A将松弛。

【解析】设O2A刚好拉直，但其拉力F2仍为零时角速度为ω1，此时∠O2O1A=30°,设O1A产生的拉力为F1,对小球：

在竖直方向F1cos30°=mg……①

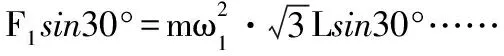
设O1A由拉紧转到刚被拉直，F1变为零时角速度为ω2

对小球F2cos60°=mg……③

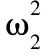
【解题技巧】圆周运动中临界问题分析，应首先考虑达到临界条件时物体所处的状态，然后分析该状态下物体的受力特点，并确定向心力，再结合圆周运动的知识，列出相应的动力学方程求解。

二、竖直平面内圆周运动的临界问题

竖直平面内的圆周运动是典型的变速圆周运动，一般情况下，只讨论最高点和最低点的情况。这类题目的综合性强，涉及的知识点多，物理情景变化空间大，是我们复习中的难点。我们在解题时应充分分析研究对象的受力和运动情况，建立其运动的物理模型，运用动力学、功能关系和动量观点等知识来综合解题。

【例3】如图3所示，让摆球从图中的C位置由静止开始摆下，摆到最低点D处，摆线刚好被拉断，小球在粗糙的水平面上由D点向右做匀减速运动，到达A孔进入半径R=0.3 m的竖直放置的光滑圆弧轨道，当摆球进入圆轨道立即关闭A孔。已知摆线长L=2 m，θ=60°，小球质量为m=1 kg，D点与小孔A的水平距离s=2 m，g取 10 m/s2。试求：

(1)求摆线能承受的最大拉力为多大？

(2)要使摆球能进入圆轨道并且不脱离轨道，求粗糙水平面摩擦因数μ的范围。

【动态分析】摆球从C到D运动过程中在竖直平面内做加速圆周运动，在D点摆线刚好被拉断，说明此时摆线承受的拉力达到最大；小球从D到A运动过程做匀减速直线运动，进入A孔后沿圆轨道做竖直平面内的圆周运动，要使摆球不脱离轨道，可能有两种情况，一是在到达圆心等高处之前停下来；二是顺利通过最高点。

【解析】(1)当摆球由C到D运动过程做圆周运动，摆球的机械能守恒：

摆球在D点时，由牛顿第二定律可得：

联立两式可得：

Fm=2mg=20 N。

(2)要使摆球能进入圆形轨道，则摆球到达A孔时速度必须满足：vA≥0

摆球从D到A运动过程由动能定理可得：

联立两式可得：μ1≤0.5

①若进入A孔的速度较小，那么将会在圆心以下做等幅摆动，不脱离轨道。其临界情况为到达圆心等高处速度为零，由机械能守恒可得：

由动能定理可得：

可求得：μ2≥0.35

②若小球能过圆轨道的最高点则不会脱离轨道，在圆周的最高点，由牛顿第二定律可得：

小球从D到圆周的最高点过程，由动能定理可得：

解得：μ3≤0.125

综上，动摩擦因数μ的范围为：0.35≤μ≤0.5或者μ≤0.125。

【变式训练】例题3中，将光滑圆形轨道改成光滑的圆形管道，则要使小球做完整的圆周运动，求粗糙水平面摩擦因数μ的范围？

大家试分析一下此时的结果是否与例题3的结果相同呢？又或者改成拱形桥的话，结果又如何呢？

三、带电粒子在磁场中做圆周运动的临界问题

带电粒子在磁场中的运动是高中物理的一个难点，也是高考的热点。在历年的高考试题中几乎年年都有这方面的考题。带电粒子在有界磁场中的运动问题，对考生的空间想象能力、物理过程的分析能力以及物理规律的综合应用能力都有很高的要求。解决这类问题既要用到物理中的洛仑兹力、圆周运动的知识，又要用到数学中的平面几何中的圆及解析几何知识。

(1)粒子沿环状的半径方向射入磁场，不能穿越磁场的最大速度多大?

(2)所有粒子不能穿越磁场的最大速度多大?

【动态分析】粒子沿径向飞出，可以用“缩放圆”的方法判断出临界情况为粒子的运动轨迹恰好与外环相切，根据几何关系求出运动的轨道半径，再根据带电粒子在磁场中运动的轨道半径公式求出最大的速度。粒子沿环状域的内边界圆的切线方向射入磁场时，此时的轨道半径为最小的轨道半径，此时粒子若不能出磁场，则所有粒子都不会出磁场，根据几何关系求出轨道半径，再通过轨道半径公式求出最大的速度。

当运动轨迹恰好与外圆相切时(如图5所示)半径最大，由图中的几何关系可得：

联立上面的速度表达式并代入数据可得：

v1=1.5×107m/s

此速度即为沿环状半径方向射入的粒子不能穿越磁场的最大速度。

(2)粒子沿内圆切线方向射入磁场，轨迹与外圆相切，此时轨迹半径r2最小(如图5所示)，则有

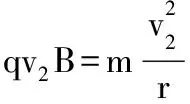
要使所有粒子都不能穿越磁场区域，必须满足r≤r2

即所有粒子都不能穿越磁场的最大速度为1.0×107m/s。

【解题技巧】临界值可能以极值形式出现，也可能是边界值(即最大值和最小值)，解题关键：画图→动态分析→找临界轨迹→确定圆心、半径和粒子射入、射出磁场边界的临界点。(这类题目关键是作图，图画准了，问题就解决了一大半，余下的就只有计算了——这一般都不难。)