三维六向变截面锥管状预制体结构建模及性能预测*

张志钢，蒋 云，李静东

(1.天津工业大学，天津 300387；2.天津城建大学，天津 300384；3.江南大学 纺织服装学院，无锡 214122)

0 引言

三维预制体与基体复合即可得到三维编织复合材料，其性能与工艺设计密切相关。三维编织复合材料比层合复合材料强度高，并具有较高的抗冲击性能和力学性能[1-2]。三维编织复合材料作为一种典型的结构与功能一体化先进复合材料，可通过三维编织整体成形异型截面的复合材料构件，结构设计灵活、力学性能优异、抗分层和抗冲击性能优良[3]，锥管状预制体就是一类典型的异型截面构件，在工程中应用广泛。

三维六向是三维五向在航天领域成功应用基础上，为满足其周向力学性能的进一步提升而开展的拓展研究。现研究已相当广泛，并取得了许多阶段性成果。刘景艳、陈利[4]采用控制体积单元法系统地研究了三维六向预成型件的纱线交织结构，在实验研究的基础上确立了编织结构参数之间的关系，推导出了纤维体积含量计算式。徐焜、许希武等[5]通过拉伸(含开孔拉伸)、压缩(含开孔压缩)、面内剪切及冲击后压缩实验，获得了三维六向编织复合材料的主要力学性能参数；探讨了材料在拉伸、压缩及剪切载荷作用下的破坏模式和失效机理；分析了开孔类型(机械孔、编织孔)对材料拉、压性能的影响并研究了冲击对材料压缩性能的影响。李典森、卢子兴等[6]在建立编织参数的数学模型基础上，采用改进的刚度平均化方法，导出了三维六向编织复合材料的工程弹性常数，分析了编织角和纤维体积含量对弹性性能的影响，研究表明，三维六向编织复合材料具有良好的力学性能，由于面内纬纱的加入，使面内的力学性能得到了提高。唐玉玲、周振功等[7]通过试验测试与数值模拟相结合的方法对三维六向编织复合材料的螺栓连接性能进行了研究，分析了单搭连接的二次弯曲现象,获得了侧向约束面积、螺栓拧紧力矩及连接平板厚度对单搭单螺栓连接结构力学性能的影响规律。张迪、郑锡涛等[8]对比研究利用相同炭纤维、基体和相同制备工艺(RTM)加工的三维多向编织和层合板复合材料的力学性能，四种三维多向编织结构分别利用三维四向、三维五向、三维六向和三维七向编织工艺制备，研究表明编织结构和编织角是影响材料破坏模式的重要因素。万振凯、张志钢等[9]针对三维六向编织复合材料编织结构，采用三维四步六向编织方法将碳纳米线传感器以轴向纱和六向纱形式嵌入复合材料中，提出了一种构建智能三维复合材料的方法，建立了基于碳纳米线的三维编织复合材料试件内部损伤监测系统。

纵观上述三维六向复合材料已开展的研究，从纱线运动规律分析入手，通过建立预制体结构几何模型和力学分析模型，对其拉伸、压缩和剪切等基本力学性能进行了系统研究，再从应用角度对包括三维六向在内的三维多向复合材料平板与层合板的力学性能进行了比较研究，最后基于碳纳米线新编织材料，把三维六向结构复合材料向智能化复合材料拓展开展了应用探索研究。上述研究为三维六向复合材料实现工程应用奠定了技术基础，但还只限于规则形状的平板预制体，对锥管状预制体为代表的异型预制体的研究还未开展深入系统研究，为实现三维六向异型预制体关键结构参数的精准设计与编织工艺优化，迫切需要开展此方面研究。

预制体是复合材料基材，只有预制体的关键结构参数实现了精准设计和精确控制，复合材料的质量一致性才能得到有力保障。为此，需深入研究三维六向锥管状预制体的细观结构。本文通过建立基于不同减纱工艺的编织单胞模型，精确设计计算锥管不同部位的纤维体积百分含量细微变化，从而为三维六向锥管状预制体的工程化应用提供理论指导。

1 三维六向变截面锥管状预制体减纱技术

三维六向是在三维五向基础上，引入周向纱线作为第六向，其减纱技术及几何结构建模与三维五向在方法上相同，且在三维多向结构中具有通用性。减纱技术可归纳为减少纱线阵列(即减阵列减纱)和减小纱线截面面积(即减细减纱)两大类[10]，逐点减纱是减列减纱的特例，减层减纱减的是周向阵列纱线。对于横截面变化的锥管状预制体须采用上述的一种或多种组合才能制备出满足设计要求的预制体。

1.1 减阵列减纱技术

减阵列减纱技术分减列向阵列、减环向阵列及其组合等(如图1所示)。

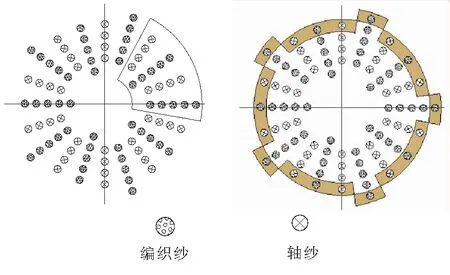
(a)减列减纱 (b)减层减纱

在减阵列减纱中，由于减环向阵列只发生在表层，内部单元结构不受影响，且工艺操作方便，被较多采用[10]。

1.2 减细减纱技术

设定每一个携纱器所携带的纱线都由更小的纤维束合股而成，当某携纱器运动至圆型机最外侧时，减去其中一股纤维束，让剩余纤维束由该携纱器携带继续向内侧运动，这时减细的纱线就与由内向外运动的未减细纱线相遇，形成带有减细纱线的单元。还可能与由内向外已减细的纱线相遇，形成不同型式的结构单元[11]。

减阵列减纱不管是在预制体表层还是内部都会留下缺陷，该处的纤维体积百分含量发生突变，对于有特殊用途的预制体可能会造成致命性的毁伤。减细减纱(如图2所示)则弥补了这一缺陷，因此该减纱技术已被广泛应用。

2 基于减细减纱技术的三维六向变截面锥管状预制体纱线结构解析

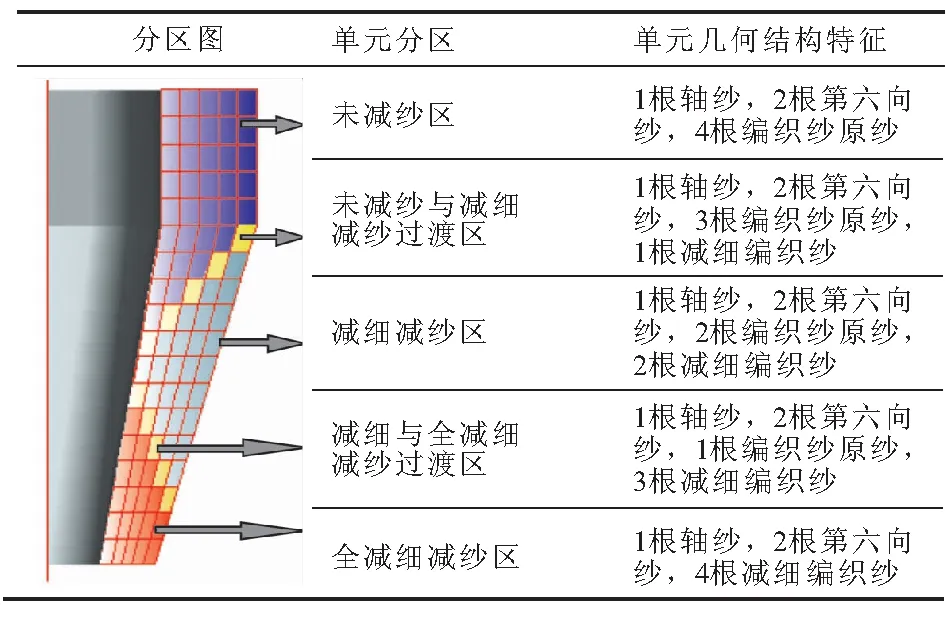
未减纱锥管状三维六向预制体单元划分与三维五向相类似，同样分为表面单元和内部单元两种类型[12]。采用减细减纱的预制体的细观结构与未减细减纱相比较，单元中纱线的交织方法并未发生改变，只是构造纱线的细度(未减细、减细和多次减细)发生了变化，根据纱线不同的构造方式把预制体分成不同的结构区域(如表1所示)，如未减纱区、未减纱与减细减纱过渡区、减细减纱区、减细与全减细减纱过渡区、全减细减纱区[13]。

表1锥管状三维六向预制体编织分区及不同区域的纱线组合结构特征
Table1Braidedpartitionsof3-dimentional-6-direnctionaltaperprefabandthecharacteristicsdifferentregionsoftheyarncombinationstructurecharacteristics

3 三维六向变截面锥管状预制体几何结构建模

锥管状横截面是由纱线截面全部填充，通过控制纱线截面减少的百分数就可精确控制预制体的几何尺寸变化。基于减细减纱建立相应的几何结构模型，在满足织物性能(纤维体积百分含量是关键设计参数)的前提下获得优化的纱线阵列和减细减纱规律(减细频次和数量等)。

3.1 基本假设

基于可变微单元设计思想[14]，对采用减细减纱的锥管状三维六向预制体作如下假设：

(1)纱线形状因编织交织和打紧过程相互挤压发生几何形状变化，但不改变纱线的横截面积；

(2)整根编织纱线在预制体内部连续，只在预制体外侧发生截面尺寸的变化；

(3)编织纱线截面为可变四边形，轴纱及第六向纱为可变菱形；

(4)预制体中心轴线为一直线，打紧平面为垂直于预制体轴线的相互平行的平面簇[14]；

(5)预制体贴膜编织，在编织过程中打紧均匀；

(6)单元尺度均匀化处理。

3.2 不同区域单元几何结构建模

在四步法编织过程中，每两步引一次第六向纱，且每个行间隔都引第六向纱，称其为全阵列三维六向编织方法，如图3(a)所示；每四步引一次第六向纱，且每个行间隔都引第六向纱，称其为半阵列三维六向编织方法，如图3(b)所示；如每两步引一次第六向纱，第六向纱间隔引入，数量只有行间隔的一半，四步后再引一次第六向纱线，与前一次第六向纱的引入位置错开，还是间隔引入，数量同样为行间隔的一半，称其为交错阵列三维六向编织方法，如图3(c)所示。本文讨论的是全阵列三维六向编织方法所形成的单元纱线结构，其余引纱编织方法以此类推，在此不再赘述。

(a)全阵列 (b)半阵列 (c)交错阵列

采用减细减纱编织技术使预制体在不同截面部位满足尺寸轮廓的边界条件，以此构造出不同分区的单元纱线组合结果，见表1。

设编织原纱截面面积为S，减细减纱截面积为Sk=fkS，纱线减细后占原纱线横截面积的百分数fk(k为减细次数)，轴纱截面面积为F，第六向纱截面面积为E。不同区域的单元结构如图4所示。

(a)未减纱区 (b)未减纱与减细过渡区 (c)减细减纱区 (d)减细与全减细过渡 (e)全减细减纱区编织纱：4×S 编织纱：3×S+1×f1S 编织纱：2×S+2×f1S 编织纱：1×S+3×f1S 编织纱：4×f1S轴纱：1×F 轴纱：1×F 轴纱：1×F 轴纱：1×F 轴纱：1×F第六向纱：2×E 第六向纱：2×E 第六向纱：2×E 第六向纱：2×E 第六向纱：2×E

3.3 未减纱单元建模

设该织物的纱线在yz面的环状有效阵列为M×N(M为环向阵列数，N为径向阵列数)，织物三维空间内表面曲线可由描述芯轴的外轮廓线绕轴线回转而成(如图5所示)。过轴线的平面将这种织物分割。描述芯轴的外轮廓线平面曲线R1=F0(x)(直管状构件为R1=常数)，即是该织物的内表面轮廓线。用于分割微单元的同轴曲面的轮廓线的曲线簇方程为Ri=Fi(x)(共N个曲面，0≤i≤N,整数)，编织花节的长度为δ，等于预制体表面轴向花节长度的1/2，可通过测量换算确定。在对预制体进行分割时取平面簇xn=nδ(0≤n≤H/δ为整数，H为预制体的轴向高度)。在坐标系中，可以认为该面为织物的打紧平面，锥管状预制体为轴对称结构，取其轴剖面作为分析对象。

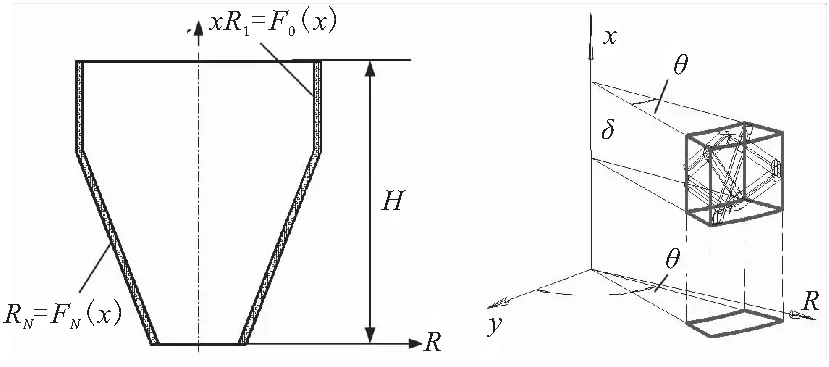
图5 三维六向锥管状预制体及其单元几何模型Fig.5 3-dimentional-6-direnctional taper prefab and unit geometric model

(1)忽略织物表面单元与内部单元的不同，任意可变微单元的体积计算

在垂直于x轴的平面内，第n+1层第i+1个代表性可变微单元的体积表达式：

(0≤i≤N-1,0≤n≤H/δ;整数)

(1)

(2)描述四边形编织纱、轴纱和第六向纱截面形状的几何参数

S=λS0(λ≤1)

(2)

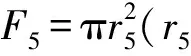
F=λ5F5(λ5≤1)，F=0.5×c×d

(3)

E=λ6E6(λ6≤1)，E=0.5×j×k

(4)

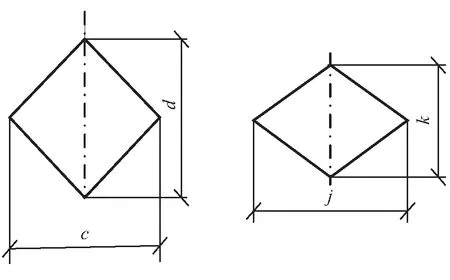
(a)轴纱截面参数 (b)第六向纱截面参数

(3)单元的体积

用长方体单元等效回转体预制体单元的扇形体，长方体几何结构参数：长A、宽B、花节δ，径向增量与长方体单元宽相等，如图7所示。根据图7所示几何尺寸关系，可得各参数之间的相互关系：

A=c+j

(5)

B=h+d

(6)

l+k=δ/2

(7)

B/A=d/c

(8)

j/k=A/δ

(9)

预制体长A或宽B可独立设计，B随A的变化而变化，花节δ由最终打紧程度决定。

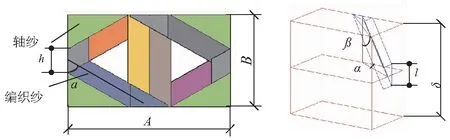
图7 用于等效预制体单元的四方体单元几何结构Fig.7 Geometric of tetragonal unit for equivalent prefab

(4)描述四边形编织纱线倾斜状态的方向角α、β

反映纱线倾斜状态的方向角α、β如图8所示[14]。建立局部坐标系xyz，x向指向编织方向。

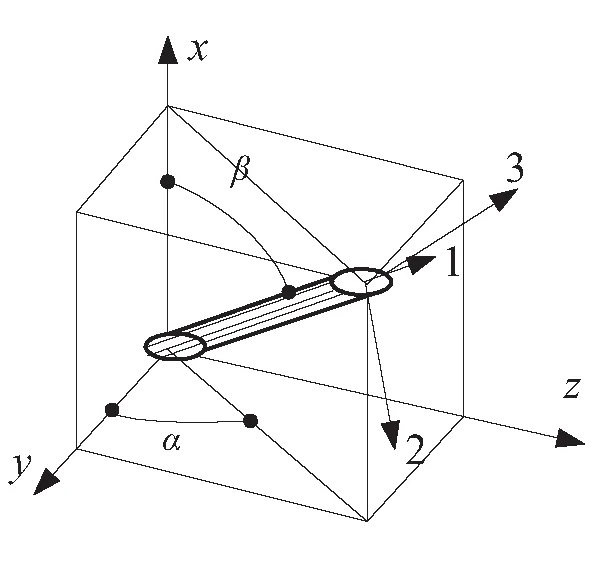
图8 方向角α、βFig.8 Direction angle α and β

方向角α、β的表达式为

(10)

tanα=A/B

(11)

(5)锥管状预制体的轴剖面外廓曲线

用可变微单元的几何特性推导三维六向锥管状预制体外轮廓几何尺寸，由式Ri=Fi(x)推得描述任意可变微单元在整体坐标系内外轮廓曲线通式：

Ri+1=Fi(x)+ΔRi+1

(0≤i≤N,N为纱线径向可变微单元的层数)

(12)

三维六向锥管状预制体最外层轮廓曲线方程：

(13)

(6)可变微单元体积

可变微单元的体积被等效为一长方体体积。等效时单元体积不变，纤维体积百分含量不变，等效前后花节相等。可变微单元的体积：

(14)

由上式进一步推得单元径向厚度：

(15)

(7)纱线体积

由图8可看出，分布于长方体中的4根编织纱用解析几何的方法计算获得其长度；轴向纱的长度即花节长。纱线的总体积：

(16)

(8)三维六向锥管状预制体纤维体积百分含量

由纱线体积和单元的体积可得出某坐标位置的单元纤维体积百分含量：

(17)

在预制体的同一横截面内对在径向排列的不同减细减纱状态的单元径向厚度进行累加，即可得到相应位置的预制体径向厚度和预制体外径尺寸，从而确定整体锥管状三维六向预制体的几何轮廓尺寸。

4 不同减细数量条件下预制体纤维体积百分含量对比分析

4.1 编织方案

采用相同的阵列数和相同的内、外轮廓尺寸边界条件，并设定每次每个最外侧携纱器上的纱线减细工艺相同。优选三种典型且具有工程应用意义的减细工艺，即每个机器循环都减细运动至机器最外侧的携纱上纱线、间隔一个机器循环减细运动至机器最外侧的携纱上纱线、不减细减纱，对其内部不同部位的纤维体积百分含量分布情况进行对比分析，得出规律性结论指导编织工艺优化。

4.2 编织参数

(1)纤维品种及规格：日本东丽炭纤维T300B-3000-40B；

(2)四个方向编织纱422列×28层，3K×3合股，第五向轴向纱422列×27层，平均为4.5K(即3K×3合股和3K×2合股梅花式间隔排布)，第六向纱27层，3K×2合股，沿周向引入；

(3)等母向花节长度编织(50～52 mm /10个花节)，纤维体积百分含量50%～53%；

(4)大端内径248 mm，大端外径284 mm，大端直柱高120 mm，小端内径80 mm，小端外径135 mm，小端直柱高40 mm，锥段高413 mm。

纤维体积百分含量分布情况如图9所示，可见：

(1)在确定的纱线阵列和内外轮廓尺寸的限定条件下，可以采取不同的减细减纱规律编织成形，不减纱是减细减纱的一种特殊形式，减细的纱线数量为零。

(a)隔一个四步减细减纱

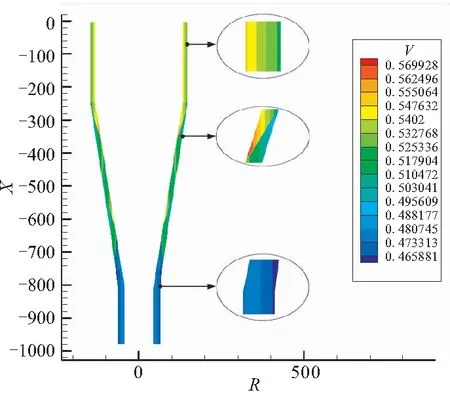
(b)每个四步全减细减纱

(c)不减纱

(2)不减纱的锥管状预制体小端纤维体积百分含量高，达0.569，纤维体积百分含量过分高，预制体变形小，会造成小端不贴模，达不到内部轮廓尺寸要求，实际编织中不采用。

(3)隔一个四步减细减纱即隔一减纱，每个四步全减细减纱即全减纱锥体的大、小端纤维体积百分含量分布均匀，小端也没有纤维体积百分含量特高的区域，都可采用。

(4)进一步比较隔一减纱和全减纱发现，其大端内侧均存在局部高体积百分含量区域，由于预制体复合完后内外表面还要磨削，正好把此去除，所以不影响整体的使用性能，纤维体积百分含量基本能控制在±0.03范围内，而且全减纱比隔一减纱在单元体积百分含量变化梯度上更小，工艺质量更易控制。因此，全减纱在锥管状预制体编织中被普遍采用。

5 变截面锥管状三维六向预制体外轮廓尺寸形状预测

采用相同的阵列数、相同的内轮廓几何尺寸和相同的打紧工艺，比较全减纱、隔一减纱和不减纱三种减细减纱方式下锥管状预制体的外轮廓几何尺寸和理论轮廓的偏差度，如图10所示。

图10 不同减细工艺三维六向锥管外轮廓几何尺寸对比Fig.10 Comparison of geometric size of 3-dimentional- 6-direnctional taper external contourin different thinning and reducing processes

由图10可以看出，全减纱外轮廓尺寸与理论值总体吻合最好，隔一减纱次之，但两者在不同部位互有正负，不减纱偏离度最大，且在小端与理论外轮廓线偏离度最大，这也验证了不减纱小端不贴模的分析结果。为了要进一步减小纤维体积百分含量的变化梯度，缩小实际外轮廓几何尺寸与理论值的偏差范围，可把全减纱和隔一减纱组合使用，使预制体纤维体积百分含量的变化更为均匀，预制体厚度的变化更为平滑，便于后续复合加工。

调整纱线几何参数、纱线阵列等编织工艺参数和减细减纱规律可达到既满足预制体的纤维体积百分含量变化区间又满足外轮廓几何尺寸的目的，此为正向设计。反向设计则可根据预制体的外轮廓几何尺寸和纤维体积百分含量的变化区间，通过调整减细减纱规律，优化编织工艺参数并使纤维体积含量变化梯度实现最小化。

针对本文的理论推导结果编写了应用程序，可对不同大小端直径和不同阵列的全减纱、隔一减纱、不减纱的三维六向预制体的纤维体积百分含量和外轮廓几何尺寸进行理论预测。

6 结论

(1)纤维体积百分含量是预制体设计的关键参数之一，为实现其梯度变化的最小化，可采取减细减纱编织工艺，在不同编织部位(由大端向小端编织)更要采取全减纱和隔一减纱两种不同减纱组合方式来实现。

(2)通过调整编织工艺参数(如纱线的几何尺寸、纱线阵列数、编织花节长度等)，可制备出满足外轮廓几何尺寸要求的预制体。根据锥管状预制体的外轮廓几何尺寸和纤维体积百分含量变化范围，通过调整减细减纱规律，可优化设计编织工艺参数，为不同用途异型预制体设计提供理论指导。