基于多评价准则融合的特征选择方法

于宁宁，刘 刚，刘 森，曹冰许

(河南科技大学 信息工程学院，河南 洛阳 471023)

0 引 言

特征选择是以提高分类效率为目的，选择最优特征子集的过程[1]。特征选择方法有Wrapper和Filter两种方式[2]。其中Filter方式的评价准则主要包括：互信息[3]、ReliefF算法[4,5]、类可分性法[6,7]、Fisher比率[8]、相关性[9]等。然而，Filter方式采用单评价准则，并不能全面评价特征集的优劣。将不同的评价准则借助信息融合方式进行融合，使其取长补短便成为研究的热点。李晓等[10]提出选择精度有所提高的融合选择方法；吴迪[11]利用融合方式获取组合证据体的最终评价结果。但是这两种方法均存在融合重要性权值系数主观确定的问题。

在本文的研究中，首先利用ReliefF算法、互信息和类可分性法3种评价准则分别对特征进行评价；然后，为克服特征重要性权值系数确定的主观性，利用序关系分析法[12,13]确定3个评价准则的重要性权值系数，采用多评价准则的融合模型综合评价结果；最后利用支持向量机从融合后的特征集中选择出最优的特征子集。

1 特征选择方法概要

特征选择主要研究从已知的特征集中，利用各种评价准则选择最优子集，达到降低计算代价、提高分类性能的目的。

1.1 ReliefF算法

Kononerko为了解决多分类问题和回归问题，提出ReliefF算法。它的核心是依据权重选择特征，选出与类别相关性强的特征，而相关性弱的特征彼此远离。其计算公式定义如下

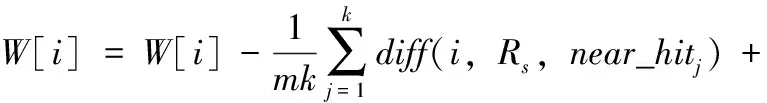
(1)

式中：i、W[i]、m、Rs、p(C)、near_hitj、near_missj的定义请参见文献[10]。

使用权值作为ReliefF算法的评估值，当其权值大于0的时候，表示特征是相关的；当其权值小于0的时候，表示特征不相关。

1.2 类可分性法

类可分性法是通过计算类内和类间的距离之比。它的特点是计算方法简单，计算效率较高

(2)

(3)

(4)

分子表示类内的欧式距离，其值越小越好，分母表示类间的欧式距离，越大越好。因此，J(i)越大，表示该特征的分类能力越强。

1.3 互信息

两个变量的互信息指两个特征共同含有的信息量：在已知一个变量的前提下，另外一个变量在不确定度方面的减少量。这个不确定度使用信息熵来度量。假设一个数据集D，它是由n个特征 (f1,f2,…,fn) 表示N个实例。使用概率函数p(ft)表示特征ft为不同可能值ft的概率。离散特征ft的信息熵H(ft)表示如下

(5)

在已知另一个特征c的取值之后，ft取值的不确定度可以由条件熵H(ft|c) 来度量

(6)

在此基础上，特征ft与特征c的互信息定义为

I(c;ft)=H(ft)-H(ft|c)=I(ft;c)

(7)

最后，分别计算每个特征与其余特征的总体互信息即score(ft)，可以表示为

(8)

可见，特征的总体互信息越大，表示特征包含的信息越多，特征也就越重要。

2 基于多评价准则融合的特征选择方法

为了发挥每个评价准则的优点，把不同的评价准则相互融合。本文提出基于多评价准则融合特征选择方法，其框架如图1所示。

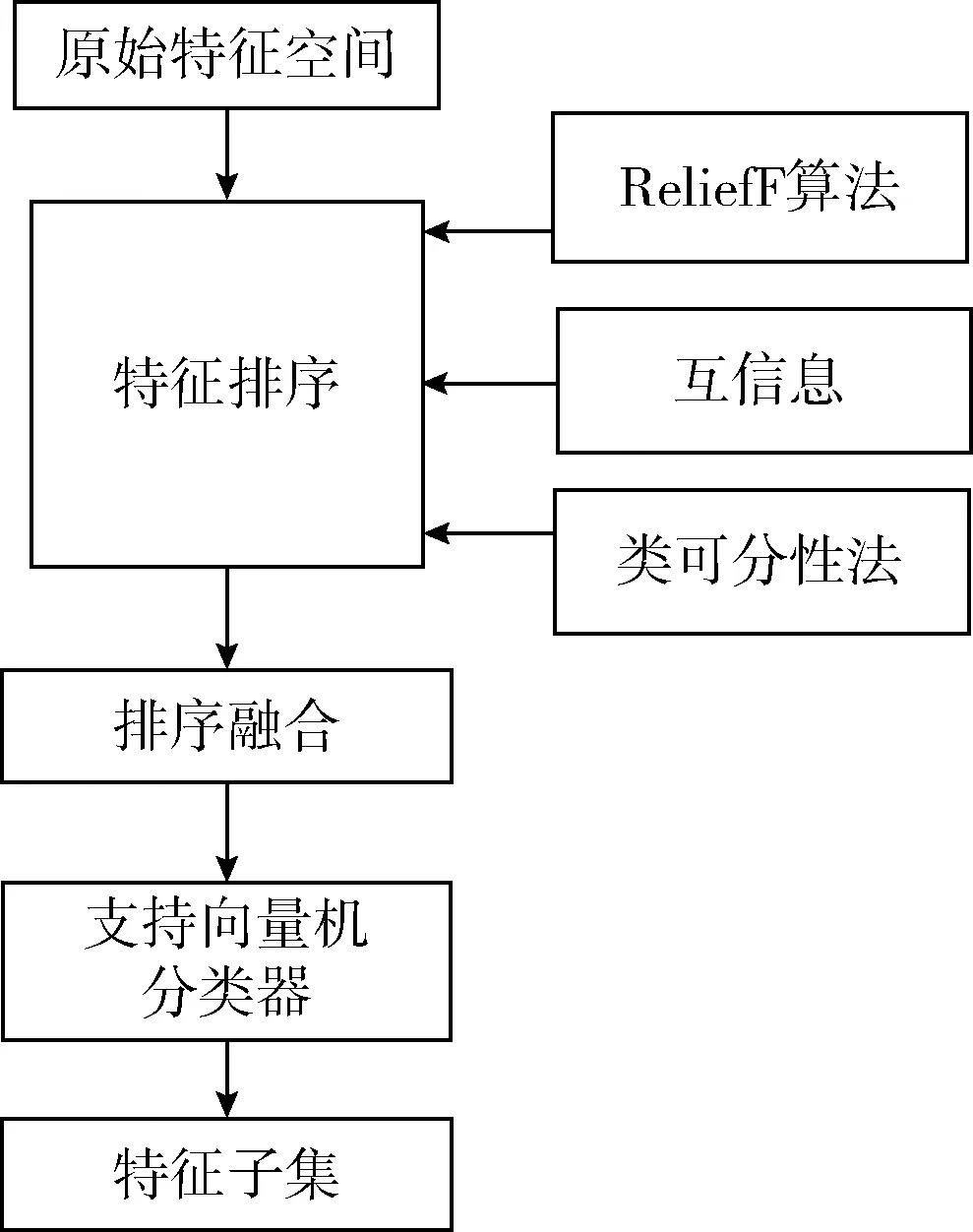
图1 基于多评价准则融合的特征选择方法框架

2.1 多评价准则融合模型

在特征选择过程中，分别采用ReliefF算法、互信息和类可分性法3种评价原则对特征进行排序。这3种评价原则均是计算的权值越大，该特征的分类性能越强，那么权值越大的特征的排序序号就越小。根据权值大小进行降序排列，得到3个排序结果，分别表示如下

Sort(ReliefF)=[SR(1),SR(2),…,SR(i),…，SR(N)]

(9)

Sort(类可分性法)=[SJ(1),SJ(2),…,SJ(i),…,SJ(N)]

(10)

Sort(互信息)=[SH(1),SH(2),…,SH(i),…，SH(N)]

(11)

其中，N表示为原始特征空间的特征维数，SR(i)、SJ(i)和SH(i)分别表示在ReliefF算法、互信息和类可分性法3种准则下第i个特征在N维特征集中的权重排序序号。

将ReliefF算法、互信息和类可分性法3种准则的排序结果通过添加重要性权值系数的方法进行融合处理，得到综合排序结果，表示如下

SortF,J,H=[S(1),S(2),…,S(i),…,S(N)]

(12)

S(i)=ω1SR(i)+ω2SJ(i)+ω3SH(i)

(13)

在式(13)中，ω1、ω2和ω3分别表示不同评价准则的重要性权值系数。S(i)是经过融合处理后第i个特征在N维特征集中的权重排序序号。

2.2 基于序关系分析法的重要性权值系数的确定

序关系分析法是基于层次分析法改进的计算权值方法，是一种定性和定量相结合、层次化的分析方法。它因无需构建判断矩阵和一致性检验使计算量减小；在应用中对评价方案个数没有限制，可以规避层次分析法的弊端。它的具体算法如下：

(1)确定3种评价准则的序关系。针对3种评价准则的重要性程度进行判断；按照3个评价准则的重要程度，列出3种评价准则的序关系，如下所示

U1≻U2≻U3

(14)

式中：由于ReliefF算法和类可分性法是根据特征对样本类别的区分能力来评价特征的重要性，而互信息是根据特征与特征间所含有的信息量大小来评价特征的重要性，所以从分类性能角度考虑，ReliefF算法和类可分性法的重要性程度比互信息大；ReliefF算法核心是根据被选择的样本和两个最近邻样本间的距离来评价特征，运行效率高，而类可分性法仅根据类内和类间的欧式距离来进行特征评估，因此从分类性能角度考虑，ReliefF算法比类可分性法的重要性程度大。据此，U1、U2、U3分别指ReliefF算法、类可分性法和互信息。

(2)确定两个相邻评价准则间的重要性程度之比的理性判断值。对评价准则Up-1和Up的重要程度之比ri进行理性判断，ri的赋值参考表请参见文献[13]。ri重要性程度之比公式如式(15)所示

(15)

根据式(15)和ri的重要性程度之比的赋值参考表，对3种评价准则的序关系中相邻准则的重要性程度之比进行理性判断，其判断值分别为

(3)计算重要性权值系数。评价准则的重要性权值系数和其在序关系中相应位置的重要性权值系数是对应一致的。重要性权值系数的计算公式为

(16)

ωp-1=rp×ωp

(17)

根据式(16)和式(17)，计算可以得到

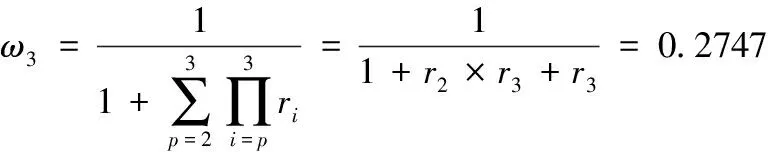
据此，可以获得式(12)中3种评价准则的重要性权值系数。将重要性权值系数代入式(13)，即可得到特征融合排序值，进而得到综合排序。

在综合排序的基础上，利用支持向量机实现最终特征选择结果。

3 实验与讨论

为了测试本文提出的基于Filter方式的多评价准则融合的特征选择方法的分类能力的高效性和性能的稳定性，本文利用UCI数据集的Iris、Wine和Ionosphere 这3个数据集设计实验。在3个实验中，采用支持向量机分类器，实验均重复50次，采用实验的平均值作为最终结果；测试样本分为两部分：训练样本和验证样本；采用Intel i5的CPU、4 G的内存的测试环境；针对上述3种评价准则分别进行实验；使用式(13)的加权参数规则和利用式(16)、式(17)计算出的重要性权值系数进行本文所提方法的实验。

3.1 基于Iris数据集的实验

为验证本文所提出的方法，本实验采用Iris数据集。拥有150个数据样本的数据集被分为每类含有50个样本点的3种类别的鸢尾花，而每个样本点包含4个属性特征，分别用来描述鸢尾花的花萼和花瓣的长度、宽度。首先从3个类别样本中分别随机抽取60%(合计90个)作为训练样本，剩余的40%(合计60个)作为测试样本。实验结果如表1、表2和图2所示。

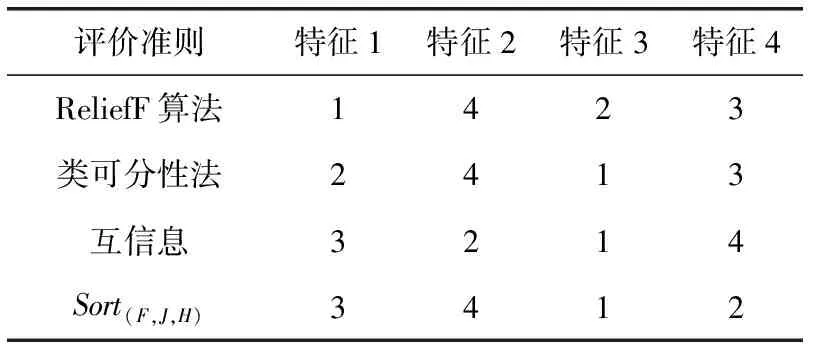
表1 数据集Iris的排序实验结果

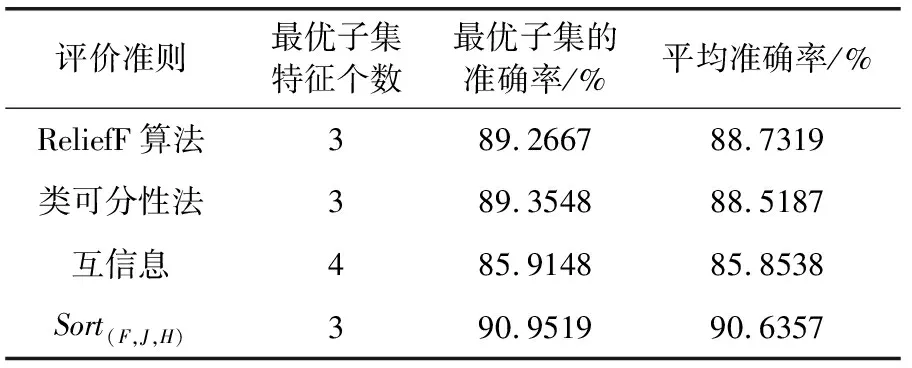
表2 数据集Iris的实验分类结果

图2 各种评价原则的特征选择方法的结果比较

在表1中，显示特征的重要性排序序号。其中特征3和特征2融合处理后的重要性排序序号为1和4，说明特征3的重要性权重最大，对分类的贡献最大；特征2的重要性权重最小，对分类的贡献就最小。

3.2 基于Wine数据集的实验

为验证本文所提出的方法，本实验采用Wine数据集。它包含有178个数据样本，一共分为3类葡萄酒，分别为59、71、48个数据样本点，每个数据包含13个属性，分别从色调、碱度、颜色强度、所含苹果酸、原花青素等角度描述葡萄酒。首先从3个类别样本中分别随机抽取60%(合计99个)作为训练样本，剩余的40%(合计79个)作为测试样本。实验结果如表3～表5和图3所示。

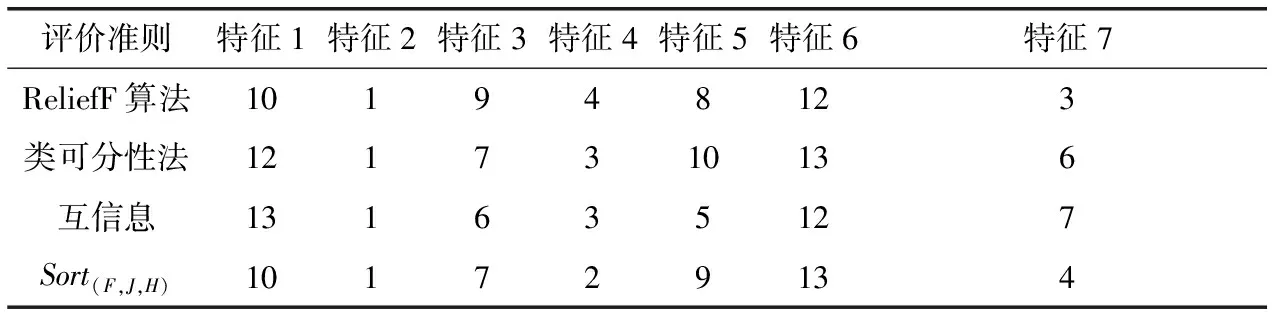
表3 数据集Wine的排序实验结果

表4 数据集Wine的排序实验结果

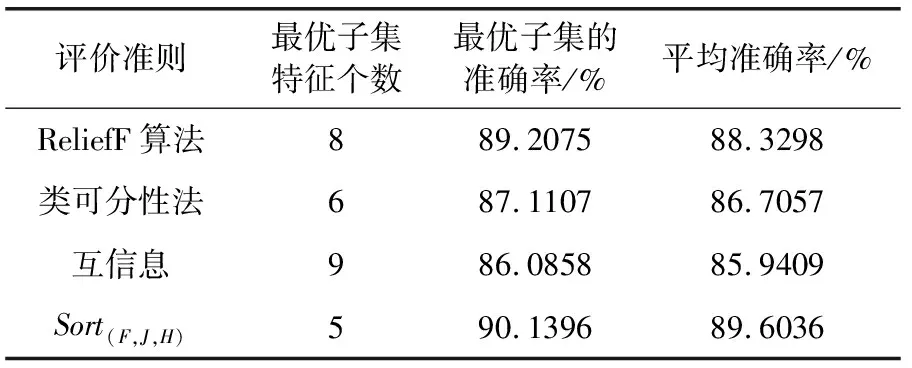
表5 数据集Wine的实验分类结果

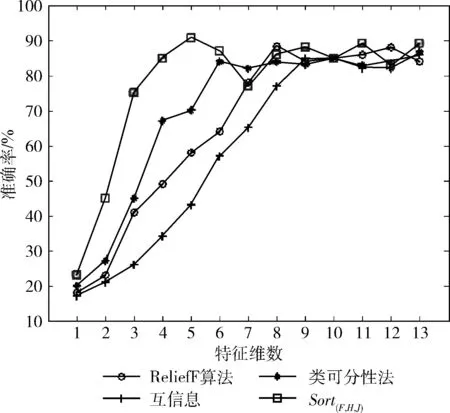
图3 各种评价原则的特征选择方法的结果比较

在表3、表4中，显示特征的重要性排序序号。其中特征2和特征6融合处理后的重要性排序序号为1和13，说明特征2的重要性权重最大，对分类的贡献最大；特征6的重要性权重最小，对分类的贡献就最小。

3.3 基于Ionosphere数据集的实验

为验证本文所提的方法，本实验采用Ionosphere数据集。它是一个二元分类问题的电离层数据集，它需要根据给定的电离层中的自由电子的雷达回波预测大气结构。该数据集包含了表示阴性和阳性的2个类别、17对雷达回波数据即34维特征和有351个样本点，其中第一类样本点为225个，第二类样本点为126个。首先从两个类别样本中分别随机抽取60%(合计211个)作为训练样本，剩余的40%(合计140个)作为测试样本。实验结果如表6和图4所示。

表6 数据集Ionosphere的实验分类结果

3个实验的结果表明：在分类准确率方面，本文所提方法比单个的评价准则有所提高，有效地降低了最优子集的特征维数，并且在分类过程中具有良好的鲁棒性。

4 结束语

本文提出了基于Filter方式的ReliefF算法、互信息和类可分性法的多评价准则融合方法，通过序关系分析法计算特征重要性权值系数，最后利用支持向量机从融合后的特征集中选择出最优的特征子集。它使3种评价准则之间取长补短，不仅拥有较高的分类识别率，而且拥有良好的稳定性和适应性。

基于多评价准则融合特征选择方法，虽然计算效率较高，但是在特征选择方法重要性程度判断上存在一定的主观性。在后续研究中，考虑利用证据组合方法计算特征重要性权值进一步保证其客观性。