物联网中基于位置的数字签名方案
阙梦菲 张俊伟 杨 超 杨 力 马建峰 崔文璇
(西安电子科技大学网络与信息安全学院 西安 710071) (jwzhang@xidian.edu.cn)
物联网是新一代信息技术的重要组成部分,它通过传感设备按照约定的协议把各种网络连接起来进行信息交换,以实现智能化识别、定位、跟踪、监控和管理[1-2].随着物联网应用越发普及,其安全问题也受到越来越多研究者的关注.文献[3]中讨论了物联网主要应用场景(智能家居、智能医疗、车联网、智能电网、工业与公共基础设施)中的隐私保护、入侵检测等安全问题.在物联网中,成千上万的物联网设备无时无刻不在产生大量的数据.因此,保障物联网设备与数据安全成为了重中之重[4].
在很多物联网应用中,节点采集的信息和节点本身位置信息是密切相关的.因此,“物”的位置信息将在物联网发展和应用中占据重要地位.只有结合节点自身位置,才能进一步获得“在什么位置发生了特定事件”[5].因此,物联网定位[6]与节点位置感知[7]是物联网研究的主要课题之一;而随着基于位置服务(location-based service, LBS)[8]大规模的部署,也产生了越来越多具有时空属性的移动数据[9];在许多应用中,如智能运输系统中,研究者收集流动的汽车数据(跟踪交通工具的位置),可以用于挖掘交通模式,使用这些数据进行交通拥塞控制[10];环境监测系统中,使用无人机进行定点传感器数据收集(温度、湿度、压力、火警等),可以实现对定点的环境探测[11].然而,对于这些时空敏感的数据,安全问题成为了一个至关重要且急需解决的问题.
物联网中时空敏感的数据面临3个挑战:
1) 传统网络中的攻击依然存在.物联网同样面临已有网络的各种攻击,攻击者可以篡改数据信息.同时,感知设备的系统可能存在漏洞和安全缺陷,攻击者可以对系统的硬件、软件及其系统中的数据进行攻击.这会导致某些数据流的篡改和虚假数据流的产生,造成消息篡改、伪造数据等攻击.然而,物联网中的海量感知设备通常性能受限,使用传统公钥数字签名解决消息篡改问题的方案计算效率较低,不适用于物联网中资源受限的感知设备.
2) 时空敏感数据的数据源位置及数据生成时间伪造.对于时空敏感的数据,必须确保消息来源的地理位置以及消息产生时刻的正确性,才能进行下一步的应对工作.然而,在物联网中,设备和网络面临各种恶意或非恶意攻击,而且,海量物联网设备自身可靠性难以保障.如果由于攻击或者故障,造成数据源位置和数据生成时间的错误(如位置错误的火警信息),有可能会造成经济损失、社会灾难等严重后果.然而现在还缺少对物联网中数据源位置及时间验证的有效方案.
3) 海量感知设备的密钥管理困难.在传统密码学中,通信双方进行身份和数据认证有2种主流方法:1)使用预共享密钥,这需要双方预共享一个对称密钥,只有通信双方持有密钥,才能够进行身份和数据认证.对于海量感知设备,基于预共享的密钥管理机制导致密钥空间爆炸,无法满足大规模应用.2)使用非对称密钥,这要求发送方持有有效的公钥证书证明自己公私钥的正确性,这必然会引入公钥基础设施;同时,管理海量设备的证书也会带来大量开销.然而由于物联网中存在海量的感知层设备,同时产生海量的数据,无论使用第1种的预共享密钥方案,或是第2种的公钥证书方案,都将带来密钥管理复杂低效的问题.
传统的数字签名中发送方以其私钥签名数据,接收方用对应的公钥解密来验证签名的真实性[12].其目的是使签名者对数据进行签名并且无法否认,任何人无法伪造签名.主要的应用包括:发送者的身份认证、保证信息传输的完整性、防止交易中的抵赖发生等.数字签名经过人们几十年的探索,研究出了许多不同的方案,如无证书签密[13]、可修订数字签名[14]、属性签名[15]等.尽管数字签名方案可以解决网络中消息篡改问题,但是对于数据源位置及数据生成时间伪造和物联网中海量数据验证的密钥管理问题仍然无法有效解决.
在这之前,Liu和Ning针对无线传感器网络提出了一个基于位置的密钥预分发方案[16];Yang和Xiao应用基于网格多项式的密钥建立来解决无线传感网络的安全问题[17];Huang等人针对无线传感网络提出了一种基于位置的密钥管理方案[18];Younis等人则提出了一种基于位置的分布式密钥管理方案[19];Zhang等人结合用户身份和地理位置得出基于位置密钥,并提出了一种基于位置的安全机制[20];2009年Chandran等人在欧密会上提出位置密码学[21],它将参与方的地理位置作为身份的凭据;在BRM(bounded retrieval model)[22]或BSM(bounded storage model)[23]模型下,实现了可证明安全的安全定位协议(secure position, SP)[21]和基于位置的密钥交换协议(position-based key exchange, PbKE)[24].安全定位协议本质上是位置验证协议,即验证者能够对证明者所处的地理位置进行验证;而密钥交换协议能够在验证者与处在期望位置的证明者之间完成密钥交换.基于位置密码学提出后,一些量子计算环境下基于位置的密码协议也随之出现[25-26].
薛庆水等人提出了基于位置的数字签名协议[27]和基于位置的代理签密协议[28],使用安全定位协议构造基于位置的数字签名.然而,薛的方案未考虑移动设备使用时的动态情况,无法实现密钥与用户位置的动态绑定.当签名者位置发生变化后,签名者仍可使用过期的密钥生成签名,无法满足基于位置数字签名的安全需求.
针对以上情况,本文提出了面向物联网设备的基于位置数字签名方案,在此方案中数据发送方使用其位置为唯一凭证对数据进行签名,而不在该位置的用户无法伪造签名.该方案既考虑签名者的位置,同时在时间方面进行严格约束,能够同时满足静态环境和动态环境下签名的不可伪造性,实现针对某个时刻处于某个位置的安全数字签名.同时该方案能够防止敌手篡改数据,并且在敌手共谋攻击的环境下满足协议的可证明安全.
本文主要贡献有3个方面:
1) 防止网络中攻击者篡改数据信息.本文方案采用计算高效的一次签名,能够防止攻击者对消息进行篡改伪造,也适用于能量受限的感知设备.
2) 防止时空敏感数据的数据源位置及数据生成时间的伪造.本文方案中数字签名使用的公私钥对的生成与数据发送方的地理位置和数据生成时间是紧耦合关系,验证签名的同时也对数据发送方的地理位置和数据生成时间进行了验证,这在时空敏感的物联网应用(如火警系统和实时交通系统)中尤为重要.
3) 感知层的设备无需密钥管理.本文方案采用PbKE协议,使得只有在期望位置的发送者才能够计算出公私钥对,即公私钥对是基于发送方位置和时间信息而动态产生的,设备无需预置的密钥,避免了面向海量感知设备的密钥管理,适合大规模物联网的应用.
1 预备知识
1.1 有界存储模型和有界检索模型
1) 有界存储模型(bounded storage model, BSM).BSM模型假设任意的参与方(包括敌手)能够存储的信息量存在一个上限.假定存在一个拥有很高最小熵(min-entropy)的信息串,若检索函数的输出长度未超过敌手能够存储的上限,则敌手就能够通过这个检索函数来检索这个信息串,并且存储检索结果.
2) 有界检索模型(bounded retrieval model, BRM).BRM模型假定所有验证者能够广播具有高最小熵的信息串,然而敌手只能提取这个信息串的一部分.在基于位置密码学中将出现这种情况:当这些信息快速经过敌手时,敌手只能够存取信息中有限的一部分.BRM模型具有2个性质:
① 验证者具有能够生成高最小熵信息串的反向块熵源.这意味着验证者自身能够生成并且发送具有高最小熵的信息串.
② 当这些信息串快速经过敌手时,敌手能够提取的信息量存在一个提取上限,设为βn.βn可以是最小熵(δ+β)n的任意部分,当且仅当检索函数的输出长度不超过βn,敌手就可以使用这个检索函数来检索信息串.
1.2 BSM伪随机生成器

根据(ε,φ)-安全的BSM PRG的定义可知,对于任意算法F,给定A(X)和K,算法F(A(X))能正确计算出G(X,K)的最大概率为ε+2-φ.在安全参数为k的情况下,如果r≥(2δ)klbn,那么ε+2-φ是可忽略的.
1.3 伪随机函数
定义2. 函数PRF[29]:{0,1}c×{0,1}R→{0,1}L是伪随机函数,当且仅当对于任意概率多项式时间(probabilistic polynomial-time, PPT)的区分器D,存在一个可忽略的函数negl,使得:
Pr[DFk(·)(1n)=1]-
Pr[Dfn(·)(1n)=1]≤negl(n),
其中,k从{0,1}n中随机选择,fn从输入输出长度均为n位的函数集合中随机选择.
2 基于位置数字签名
根据数据发送方运动模式的不同,可将发送方分为静态发送方和动态发送方.根据2种不同的运动模式,本节将分别给出2个安全定义.
2.1 符号说明
m:发送的消息;
p:发送方位置;
sk:p点私钥;
pk:p点公钥;
T:地标(landmark)对发送方位置进行验证的时刻,即协议里面X相交的时刻;
σ:发送方对消息m的签名;
v′:消息的传播速度;
ti:无线电波从地标Li到达p点所需要的时间;
安全参数:w,q,l,k;
伪随机生成器G:{0,1}n×{0,1}r→{0,1}y;
伪随机函数F:{0,1}c×{0,1}R→{0,1}L;
单向Hash函数H:{0,1}w→{0,1}q;
单向函数f:{0,1}i→{0,1}i;
公开参数:w,q,l,k,H,p,f.
2.2 基于位置数字签名的系统模型
基于位置数字签名方案如图1所示.数据发送方向地标(对于3维空间,至少需要4个地标,即L1,L2,L3,L4)证明自己所在的位置,获得由位置产生的公私钥对.获取之后立即签名消息,并将消息与签名发送给地标L1,地标验证接收时间,若符合要求,则地标对消息摘要、发送方公钥、发送方位置、数据生成时刻等进行签名,形成临时证书CertL(H(m),pk,p,T),使数据接收方能够获得位置相关的公钥来验证基于位置的数字签名.
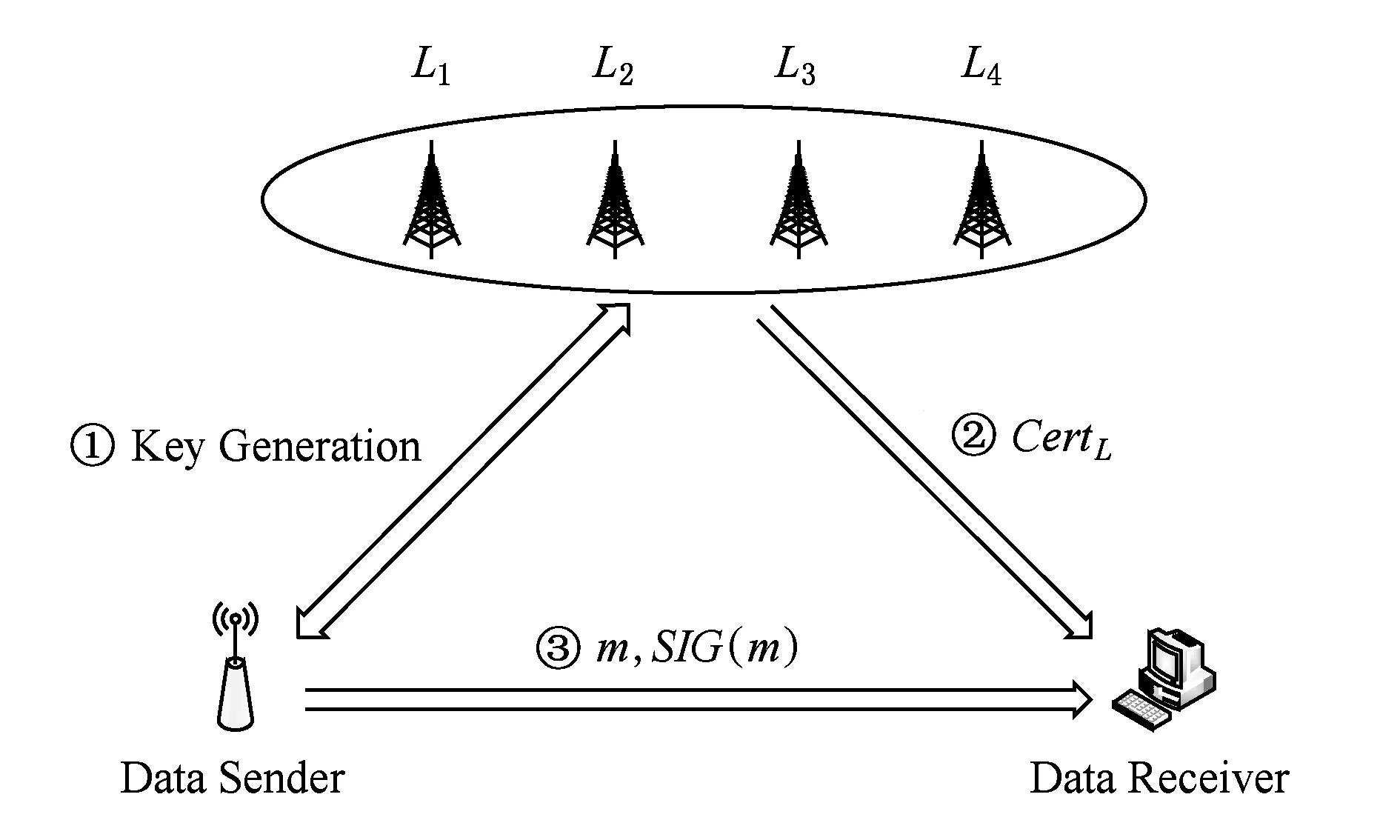
Fig. 1 Position based digital signature scheme图1 基于位置数字签名方案
2.3 静态发送方基于位置数字签名的安全定义
静态发送方是指位置不发生变动的数据发送方.由于它的位置未发生改变,继而由它的位置信息产生的密钥也未改变.
2.3.1 算法结构
时间约束下的静态基于位置数字签名算法由密钥生成算法generation、签名生成算法signature、签名验证算法verification这3部分构成,即:
(s,v)←generation(p,1k),
σ←signature(s,m,p),
f←verification(m,σ,v,p).
静态基于位置数字签名的安全需求保证只有位于p点的发送方才能生成正确的签名,且不在p点的攻击者无法伪造位置p的签名.
2.3.2 安全定义
定义3. 静态适应性选择消息攻击的不可伪造性(static EU-CMA, S-EU-CMA)当时间约束下的静态基于位置数字签名算法generation,signature,verification满足3个条件时,它满足静态签名者适应性选择消息的不可伪造性:
1) 完整性(completeness).对于来自合法位置的正确签名(s,m,p),验证签名(m,σ,v,p)输出的错误概率是可忽略的,即
Prob[verification(m,σ,v,p)=0;
(s,v)←generation(p,1k);
σ←signature(s,m,p)] <ε(k).
2) 一致性(consistency).对于任意消息m,签名的公、私钥由密钥生成算法产生,则验证签名(m,σ,v,p)在2次独立调用下会产生不同输出的概率是可忽略的,即:
Prob[verification(m,σ,v,p)≠f;
(s,v)←generation(p,1k);
f←verification(m,σ,v,p)] <ε(k).
3) 静态签名者适应性选择消息攻击的不可伪造性(static existential unforgeability against chosen message attack, S-EU-CMA).对于任意概率多项式时间(probabilistic polynomial time, PPT)的敌手A,在获得正确的签名后,可以伪造一个不同的签名(m′,σ′)的概率是可忽略的,即:
Prob[(m′,σ′)←Fsignature(s,m,p):
(s,v)←generation(p,1k);
m′≠m;verification(m′,σ′,v,p)=1]<ε(k).
2.4 动态发送方基于位置数字签名的安全定义
动态发送方是指位置会发生变动的数据发送方.随着时间的变动,发送方位置也会发生改变,当发送方从位置p移动到p′时,若仍使用定义3,将引发以下问题:发送方虽然已经离开位置p,但它仍持有p点的公私钥对,可以伪造成p点的发送方进行签名.所以定义3并不能满足动态条件下基于位置数字签名的安全需求.
2.4.1 算法结构
时间约束下的动态基于位置数字签名算法由密钥生成算法generation、签名生成算法signature、签名验证算法verification这3部分构成,即:
(s,v)←generation(p,T,1k),
σ←signature(s,m,p,T),
f←verification(m,σ,v,p,T).
时间约束下的动态基于位置数字签名保证只有在时刻T位于位置p的数据发送方才能生成正确的签名,且时刻T未在位置p攻击者或者时刻T′位于位置p的数据发送方也无法伪造时刻T位于位置p的签名.
2.4.2 安全定义
定义4. 动态适应性选择消息攻击的不可伪造性(dynamic EU-COMA, D-EU-COMA)当时间约束下的动态基于位置数字签名算法generation,signature,verification满足3个条件时,它满足动态签名者适应性选择消息的不可为造性:
1) 完整性(completeness).对于来自合法位置的正确签名(s,m,p,T),验证签名(m,σ,v,p,T)输出是错误的概率可忽略,即:
Prob[verification(m,σ,v,p,T)=0;
(s,v)←generation(p,T,1k);
σ←signature(s,m,p,T)]<ε(k).
2) 一致性(consistency).对于任意消息m,签名的公、私钥由密钥生成算法产生,则验证签名(m,σ,p)在2次独立调用下会产生不同输出的概率是可忽略的,即:
Prob[verification(m,σ,v,p,T)≠f;
(s,v)←generation(p,T,1k);
f←verification(m,σ,v,p,T)]<ε(k).
3) 动态适应性选择消息攻击的不可伪造性(dynamic existential unforgeability against chosen one message attack, D-EU-COMA):对于任意概率多项式时间(probabilistic polynomial time, PPT)的动态签名者,当它的发生位置变动之后,可以伪造成原位置产生签名(m′,σ′)正确的概率是可忽略的,即
Prob[(m′,σ′)←Fsignature(s,m,p,T):
(s,v)←generation(p,T,1k);m′≠m;
verification(m′,σ′,v′,p,T)=1] <ε(k).
显然,文献[27]中提出的方案只适用于静态发送者,即满足S-EU-CMA的定义,但不满足D-EU-COMA的定义.
3 时间约束下基于位置数字签名协议
本节在3维空间中设计了一个时间约束下基于位置的数字签名协议.数据发送方声称的位置p封闭在由L1,L2,L3,L4这4个地标围成的4面体中(对于3维空间,至少需要4个地标).G是一个(ε,φ)-安全的BSM伪随机生成器,选择合理的参数,使得ε+2-φ是可忽略的.假定L1的公钥为pkL,私钥为skL.
时间约束下基于位置数字签名协议具体过程如下:
1) 密钥生成(generation(p,T,1k)→(s,v))
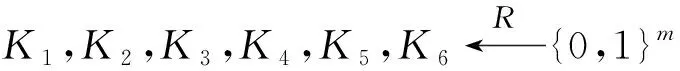
②Xi为BRM模型中具有高最小熵的随机字符串,在协议执行之前,L1生成随机串X4;L2生成随机串X1和X5;L3生成随机串X2;L4生成随机串X3.
③ 令L1在时刻T-t1广播密钥K1和X4;L2在时刻T-t2广播X1和X5;同样,L3在时刻T-t3广播X2;并且L4在时刻T-t4广播X3.
④ 在时刻T,位于p点的数据发送方同时接收到所有消息,它使用BSM伪随机生成器计算得到K2=G(X1,K1),K3=G(X2,K2),K4=G(X3,K3),K5=G(X4,K4),K6=G(X5,K5).
⑤ 数据发送方和地标Li(1≤i≤4)利用伪随机函数随机产生t个l位长度的字符串k_secret=F(K6)=(s1,s2,…,st).令k_secret等于p点私钥sk=(k,s1,s2,…,st).
⑥ 设f为单向函数,地标Li(1≤i≤4)计算v1=f(s1),v2=f(s2),…,vi=f(si),将pk=(k,v1,v2,…,vt)作为p点的公钥.
⑦ 输出(s,v)作为时刻T位于p点的公私钥对.
2) 签名生成(signature(s,m,p,T)→σ)
① 数据发送方在时刻T发送消息m,设消息m为b位,m设为介于0和2b-1的整数值,首先令h=Hash(m),将m变成固定长度的字符串,长度为klbt.
② 把h均分成每份长度都为lbt的k个子字符串h1,h2,…,hk.将每份hj化为整数值ij,1≤j≤k.
③ 从私钥sk=(k,s1,s2,…,st)中找出相对应的si j,即s的下标值与ij相等.构成k个数(si1,si2…,si k).
④ 输出σ=(si1,si2…,si k)作为数据发送方对消息m的签名.
⑤ 将消息的签名附在消息之后,立即将(m,σ,p,T)发送给地标L1,L1验证接收到(m,σ)的时间是否为T+|PL1|v′(|PL1|为p点到地标L1的距离,v′为消息的传播速度),若接收时间符合要求,则地标L1用自己的私钥skL对消息摘要、p点公钥、p点位置信息、数据生成时刻T进行签名,即CertL(H(m),pk,p,T),并广播pk,p,T,CertL(H(m),pk,p,T),使数据接收方能够使用pkL验证该签名,从而验证在时刻T时p点公钥v的正确性;反之,L1拒绝生成签名CertL(H(m),pk,p,T),数据接收方无法通过L1的签名验证时刻T时p点的公钥v的正确性.
3) 签名验证(verification(m,σ,v,p,T)→f)
① 数据接收方得到消息(m,σ,v,p,T),首先查找是否存在L1签名的广播消息pk,p,T,CertL(H(m),pk,p,T).若存在,使用L1的公钥解密,得到p点公钥pk;若不存在,则说明地标拒绝该签名.
② 当数据接收方验证公钥pk的正确性后,令h=Hash(m),将m变成固定长度的字符串,长度为klbt.
③ 把h均分成每份长度都为lbt的k个子字符串h1,h2,…,hk.将每份hj化为整数值ij,1≤j≤k.
④ 从p点公钥pk=(k,v1,v2,…,vt)中找出对应的vi j,即v的下标值与ij相等.构成k个数(vi1,vi2…,vi k).
在本方案中,BRM模型的使用方法如下:根据BRM模型的定义可知,随机字符串Xi具有高最小熵,当这些信息串快速经过敌手时,敌手能够提取的信息量存在一个提取上限,设为βn.βn可以是最小熵(δ+β)n的任意部分.也就是说敌手无法全部存储Xi,只能存储每个字符串的一部分.本文方案在协议执行前的初始阶段,地标L1生成随机串X4,地标L2生成随机串X1和X5,地标L3生成随机串X2,地标L4生成随机串X3.当这些Xi经过敌手时,敌手只能存储Si,|Si|≤βn,所以敌手只能计算Ki+1=A(Si,Ki),其中A(·,·)是任意的敌手算法.而位于p点的数据发送方能同时接收到K1以及X1~X5,所以它能使用BSM伪随机生成器计算得出Ki+1=PRG(Xi,Ki),进而得到正确密钥.
4 安全性证明
定理1. 如果G是(ε,φ)-安全的BSM PRG,F是PRF,Xi(1≤i≤4)具有最小熵(δ+β)n,βn是检索上限,f是单项函数,H是单向Hash函数,Sign满足EU-CMA[30]安全,那么本文所提协议在共谋攻击下是安全的,即满足D-EU-COMA.
证明. 不失一般性,令所有的共谋敌手{A1,A2,…,Ak}被敌手FORGER控制.令S1,S2,分别为所有敌手对X1,X2所检索的总信息,且|S1|≤βn,|S2|≤βn.
在3维空间中,假设基于位置的数字签名协议是不安全的,即存在敌手FORGER能以不可忽略的概率εFORGER伪造p点的签名.如果敌手FORGER成功攻击此协议,则存在4种可能的事件:
事件1. 敌手FORGER能够成功伪造地标L1的签名.
若敌手FORGER能够伪造地标L1的签名,它可将其公钥、p点的位置信息、用地标L1的私钥进行签名后广播.数据接收方会将敌手FORGER的公钥当成p点的公钥.此时敌手FORGER成功伪造成p点对消息进行签名.
用ε1表示敌手FORGER能够成功伪造地标L1的签名的概率,则敌手FORGER能够成功伪造p点进行签名的概率为εs(ε1=εs).很明显,这与EU-CMA的定义相矛盾,即事件1发生的概率是可忽略的.
事件2. 敌手能正确计算K.
1) 情况1. 给定(S1,K1)敌手FORGER可以计算出密钥K2=G(X1,K1).
令A1为地标L1和p点之间的敌手.S1为大字符串X1经过A1时,A1存储的总信息量.因为敌手FORGER可以计算出K2,所以当X2经过A1时,A1能够计算K3=G(X2,K2),以此类推得到K6,进而得到sk=F(K6).由此可见若敌手FORGER计算出K2,就能够得到p点的私钥sk,以此来伪造p点签名.
显然由于K1尚未经过p点,所以S1只是任意的X1的函数.此外,因为所有敌手存储的信息总量被限制不能超过βn,所以|S1|≤βn.因此,有K2=A(S1,K1),其中A(·,·)是任意的敌手算法,它的输出可能是S1和K1的一个任意的函数值.
用ε21表示敌手FORGER能够计算K2=G(S1,K1)的概率,则敌手A1能够计算出K3=G(X2,K2)的概率为
通常在安全参数l的选择下12l是可忽略的.所以,εx1与ε21近似相等,在ε21不可忽略的情况下,概率εx1也是不可忽略的.由上可知这与(ε,φ)-安全的BSM PRG定义相矛盾.由此可得,在情况1下,敌手FORGER成功伪造p点签名的概率是可忽略的.
2) 情况2. 给定(S2,K2),敌手FORGER能够成功计算K3=G(X2,K2).
令A2为地标L2和p点之间的敌手.由于FORGER能够计算K3,以此类推得到K6,进而得到sk=F(K6).由此可见如果敌手FORGER计算出K2,就能够得到p点的私钥sk,以此来伪造p点签名.
显然由于X1尚未经过p点,所以A2无法计算K2=G(X1,K1),不知道K2的情况下,S2只是任意X2的函数,并且|S2|≤βn.因此,有K3=A(S2,K2),它的输出可能是S2和K2的一个任意的函数值.
用ε22表示敌手FORGER能够计算K2=G(X1,K1)的概率,则敌手A2能够计算出K3=G(X2,K2)的概率为
同理,在概率ε22不可忽略的情况下,概率εx2也是不可忽略的.同样,这与ε-secure的BSM PRG定义相矛盾.由此可得,在情况2下,敌手FORGER成功伪造p点签名的概率是可忽略的.
3) 情况3. 由情况1,2可知位于地标L3和p点之间的敌手可以伪造p点签名的概率为
由上可知,在情况3下,敌手FORGER成功伪造p点签名的概率是可忽略的.
4) 情况4. 由情况1,2可知位于地标L4和p点之间的敌手可以伪造p点签名的概率为
由上可知,在情况4下,敌手FORGER成功伪造p点签名的概率是可忽略的.
事件3. 在不知道密钥K的情况下,敌手FORGER能够猜到p点私钥sk.
用ε3表示事件3发生的概率,如果ε3不可忽略,则可构造敌手Af以概率εf(εf=ε3)猜测出p点私钥来伪造成p点进行签名.很明显这与PRF的定义相矛盾,所以事件3发生的概率是可忽略的.
事件4. 在不知道sk的情况下,敌手FORGER能够伪造p点签名.
1) 情况1. 得到p点签名(m,σ)后,敌手FORGER可以伪造签名(m′,σ′),满足m′≠m,σ′≠σ.
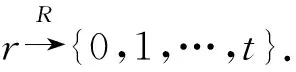
如果敌手Ax可以成功输出z使得f(z)=y,则敌手FORGER能成功伪造签名(m′,σ′)且∃j(1≤j≤k)hj=r,否则敌手Ax随机选择一个数作为z.
用ε5表示敌手Ax成功输出且f(z)=y的概率,则敌手FORGER能够成功伪造p点签名的概率为
通常情况下l至少为80 B,因此,12i=2-80.对于一般网络来说是可忽略的.由此可知,如果概率ε5是不可忽略的话,那么概率εp1也是不可忽略的.这与单向函数的定义相矛盾.所以情况1发生的概率是可忽略的.
2) 情况2. 给定(m,σ),敌手可以找到m′满足h′=h,其中h=H(m),h′=H(m′),m≠m′.
假定敌手FORGER使用Hash函数H,使得H(m)=H(m′).然而根据Hash函数H的定义,令H(m)=H(m′)的概率为ε42,则敌手能够成功伪造p点签名的概率为
通常情况下k=16,t=1024或者k=20,t=256.当k=16,t=1024时,(kt)k=(161024)16=2-96;当k=20,t=256时,(kt)k=(20256)20=2-73.由此可知,对于一般应用而言,(kt)k是可忽略.所以,情况2发生的概率是可忽略的.
综上所述,敌手FORGER能够伪造p点签名的概率为
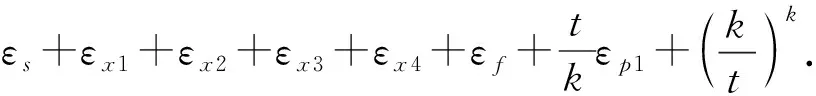
因此,如果G是(ε,φ)-安全的BSM PRG,F是PRF,Xi(0≤i≤2)具有最小熵(δ+β)n,βn是检索上限,f是单项函数,H是单向Hash函数,那么εf,εx1,εx2,εx3,εx4,εs,εp1以及εFORGER都是可忽略的.即敌手伪造签名的概率是可忽略的.定理1得证.
5 方案讨论
本文方案将数据源的位置作为凭证,对消息进行签名,保障了物联网中时空敏感数据的安全性.
5.1 防止网络中攻击者篡改数据信息
为了防止攻击者利用网络存在的漏洞和安全缺陷对物联网中的数据进行篡改,本文采用了一次签名方案.当数据发送方发送数据时,首先与地标Li(i=1,2,3,4)交互,计算得出密钥K6,k_secret=F(K6)=(s1,s2,…,st),令发送方私钥sk=(k,s1,s2,…,st).发送方用私钥签名消息得到消息签名σ,将签名附在消息之后进行广播.数据接收方收到消息及签名时,首先使用发送方公钥pk=(k,v1,v2,…,vt)进行验证,若签名验证通过,则证明数据未被篡改,若验证失败,则拒绝接收这条消息.对于物联网中的攻击者来说,由于vi=f(si)且f为单向函数,因此攻击者无法获得发送方的私钥sk=(k,s1,s2,…,st),所以无法伪造签名.因此,攻击者无法篡改消息.同时,本文使用的一次签名基于单向函数构造,相比传统的公钥数字签名,更适合物联网中能量受限的感知设备.
5.2 防止时空敏感数据的数据源位置及时间伪造
为了防止时空敏感数据的数据源位置及时间伪造,本文采用PbKE协议,使得只有在某一时刻处于某一位置的用户才能获得使用位置信息产生的公私钥对,也就是说签名使用的公私钥对与用户的地理位置和数据发送时间是紧耦合关系.当数据发送方需要发送数据时,首先与地标Li(i=1,2,3,4)交互,进行位置验证.Li广播各自的消息,使得在时刻T,数据发送方同时接收到所有消息,计算K2=G(X1,K1),K3=G(X2,K2),K4=G(X3,K3),K5=G(X4,K4),K6=G(X5,K5).将K6进行一次伪随机运算得到F(K6)=(s1,s2,…,st),令sk=(k,s1,s2,…,st)即为发送方私钥.发送方用私钥签名数据,将签名附在消息之后进行广播.L1验证签名返回的时间,若接收时间符合要求,则地标L1用自己的私钥skL对消息摘要、p点公钥、p点位置信息、数据生成时刻T进行签名,形成关于位置的临时证书CertL(H(m),pk,p,T),并广播pk,p,T,CertL(H(m),pk,p,T);反之,L1拒绝生成临时证书CertL(H(m),pk,p,T).由于发送方的公私钥对是由位置信息产生的,所以当数据接收方验证签名时,同样也验证了数据源的地理位置及数据的发送时间.当不处于发送方地理位置的敌手想要篡改数据源位置信息时,有2种办法:1)得到发送方私钥伪造数据的签名;2)伪造地标L1签名的临时证书.然而由PbKE的安全性和EU-CMA的定义可知,以上2种办法都无法实现.所以我们构造的方案能够防止物联网中时空敏感数据的数据源位置及时间伪造.
5.3 感知层的设备无需密钥管理
本文方案中,感知设备无须预先与地标共享安全通道,所有消息均通过广播方式发送.感知设备既无需事先预共享密钥,也无需公钥证书,因为签名所需的私钥sk=(k,s1,s2,…,st)是在与地标的交互过程中根据设备位置产生的,而不是借助预先的密钥管理机制生成,这避免了海量感知设备前期的密钥管理.临时证书CertL(H(m),pk,p,T)由地标验证接收时间符合要求后,利用地标的公钥生成并广播.总之,对于海量感知设备,本方案无需预先的密钥管理机制,具有可扩展性,适合大规模的部署.
5.4 签名方案的选择
使用公钥密码体制的数字签名,一旦地标L验证了发送方的位置,则该公私钥能够进行多次签名.对于动态发送方而言,当它发生迁移而离开原位置时,它仍然持有原位置的公私钥对,这显然不满足动态环境下基于位置数字签名的安全需求.因此,公钥数字签名算法只适用于静态环境的基于位置数字签名.
一次签名[31]借鉴一次一密的形式,当发送方使用密钥签名一个消息之后,必须重新与地标L进行交互,产生一个新的密钥对(pk,sk)来签名下一个消息.即使发送方发生迁移改变位置信息,也仍然需要与相应地标L交互,证明自己的位置后才能获得新的密钥对.因此,本文方案的数字签名采用一次签名方案.
6 性能分析
表1将物联网中基于位置的数字签名方案(position based digital signature scheme, PbDS)与Xue[27]、OTS[31]、RSA,ABS[32]、无证书签名[33]做对比,分别从签名者计算开销、验证者计算开销、是否需要公钥证书、密钥管理、预共享安全通道和是否结合位置信息等方面进行比较.
其中,G表示一次BSM PRG计算,F表示一次PRF计算,f表示一次单向函数计算,H为单向Hash函数,E表示群上的幂运算,e表示双线性对运算,d表示属性集大小,M表示群G中乘法运算,A表示群G中加法运算.
通过表1可以看出,与其他签名方案相比,本文方案不需要公钥证书、密钥管理以及预共享安全通道,这对于物联网中海量数据的安全管理来说,显得更加高效;并且只有本文与Xue的签名方案加入了位置信息,能够解决物联网中海量数据的数据源位置验证问题.另外,本方案发送方使用基于单向函数的一次签名,不涉及模指运算等代价较高的计算,更适合计算能力受限的感知设备.
表2将本文方案与Xue的方案做对比,分别从适用的签名者类型、协议执行前需要的条件、安全定义、基于的协议等方面进行对比.通过表2可以看出,Xue的方案需要地标与数据发送方之间使用预共享的安全通道,在物联网大规模的应用环境下,建立和维护该安全通道开销较大;而本文提出的方案不需要地标与数据发送方之间存在预共享的安全通道,减少了通信代价,提高了效率.另外,Xue的方案只适用于静态发送方,无法保证发送方位置动态变化情况下签名的安全性;而本文提出的方案既能适应静态发送方也适用于动态发送方,且能够抵御敌手的共谋攻击,满足可证明安全.
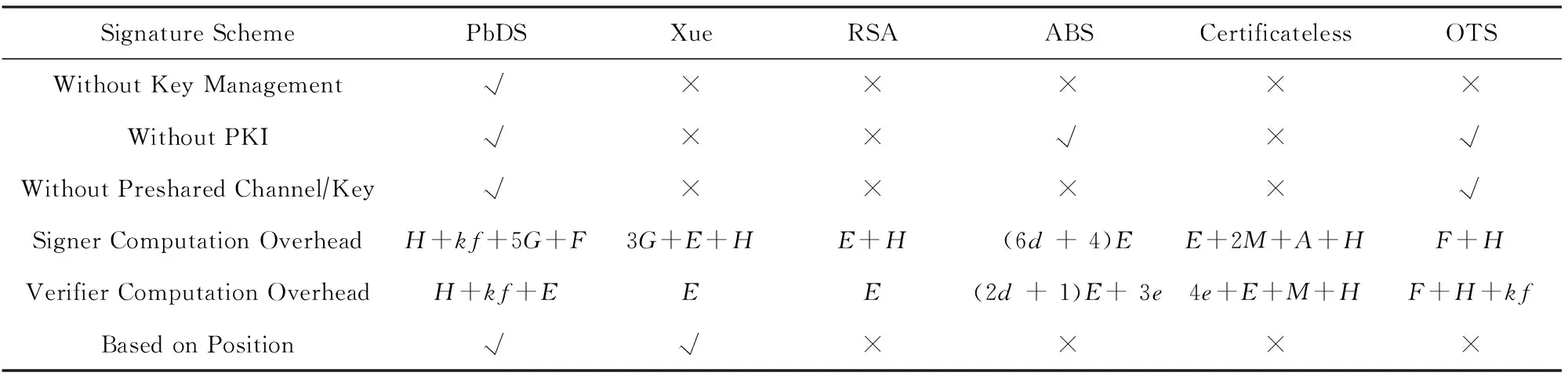
Table 1 Comparison of Signature Schemes表1 签名方案的比较
Notes:“√” means security, “×” means insecurity.
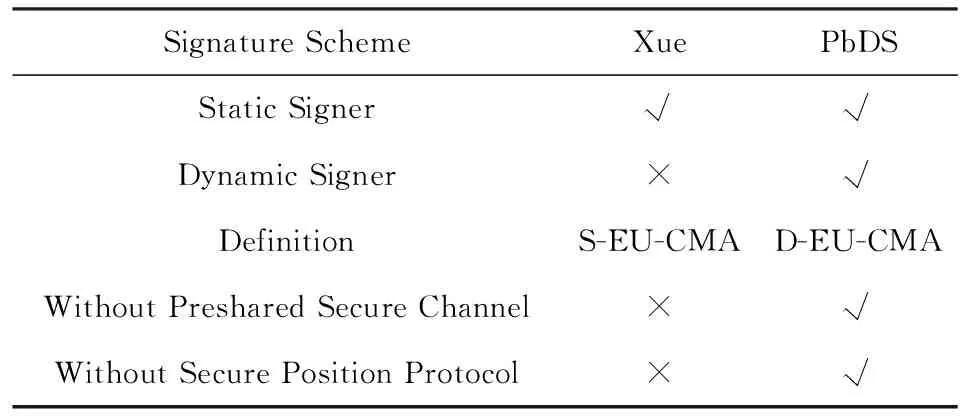
Table 2 Comparison of PbDS and Xue表2 PbDS与Xue方案的比较
Notes:“√” means security, “×” means insecurity.
7 总结与展望
本文针对物联网中数据篡改、数据源的位置验证和数据的生成时间验证等问题进行了研究.将位置特性与数字签名相结合,提出了一种解决物联网中时空敏感数据安全问题的方案.一方面,提供了数据的完整性保护;另一方面,确保了数据源的位置和时间信息的不可伪造性.本文分别提出了不考虑时间因素的静态基于位置的数字签名和考虑时间因素的动态基于位置的数字签名.然后,在BRM模型下设计出3维空间中满足动态安全需求的基于位置数字签名方案.此外,本文提出的物联网中基于位置数字签名方案能够抵御敌手的共谋攻击,且满足可证明安全.将本文方案与已有方案进行比较,在安全性方面,本文所提协议既能适应静态发送方也适用于动态发送方;在性能方面,本文所提协议使用计算高效的一次签名,不需要地标与发送方之间存在预共享的安全通道以及签名之前的密钥管理环节,减少了计算和通信代价,适用于物联网中资源受限的感知设备.
本文方案存在密钥托管问题.即每次数据发送方与地标交互得到基于位置的公私钥对的同时,4个地标也同时生成了数据发送方的公私钥对,也就是说,一旦地标被攻击者攻破,攻击者将会获得所有与地标交互的发送方基于位置的公私钥对,攻击者能够伪造发送方的签名,造成发送方密钥泄露问题.为了解决上面提到的密钥托管问题,我们下一步计划将聚合签名与基于位置相结合,设计基于位置或区域的数据聚合方案.一方面,在协议过程中地标无法计算出发送方的最终公私钥对.即便地标被攻击者攻破,攻击者也无法获得发送方的最终公私钥对,不会产生密钥泄露问题;另一方面,此方案能够确保所有数据源都来自合法位置,并且面向物联网的数据聚合能将物联网中的海量数据聚合成少量有效数据,减少了通信开销,延长了网络寿命.

