大坝水平位移监测混合模型研究

祁海燕

(辽宁西北供水有限责任公司，辽宁 沈阳 110003)

1 工程简介

恒仁水库位于辽宁省恒仁县境内的浑江中游河段。恒仁水电站为浑江梯级开发中的主力电站，同时恒仁水库也是大伙房输水工程的重要水源地水库。恒仁水库始建于1958年，1967年水库蓄水，1975年全部竣工。恒仁水库的正常蓄水位为300m，设计洪水位302m，死水位为280m。水库控制流域面积10400km2，多年平均径流量约为44.80亿m3，多年平均流量为142m3/s，多年平均输沙量为125.6万m3[1]。

枢纽工程主要由大坝、坝后式厂房、溢洪道、泄洪隧洞等建筑物组成。水库大坝为混凝土单支墩大头坝，坝顶高程为304.2m，最大坝高为78.5m，坝顶宽32.7m，坝顶长593m[2]。坝体设有表孔、中孔、底孔，分别担负着泄洪、水库正常放水以及冲砂任务。

2 监测资料分析

2.1 环境量分析

大坝水平位移分析的建模时段为2010年1月～2014年12月，预测时段为2015年1～3月。在数据分析时，只对相应时段的数据进行分析和利用。

2.1.1 上下游水位分析

恒仁水库为不完全年调节水库，从上游水位实测值来看，一般7～9月水位较高，2～4月水位较低，呈较明显的周期性变化特征。其中最高水位302.67m，超过设计洪水位0.68m，最低水位为286.04m，多年平均水位为295.54m。

水库下游水位变化比较平稳，除个别泄洪时段外，基本在247.5～249.5m之间变动。最高水位为252.51m，最低水位为247.61m，多年平均水位为248.8m。

2.1.2 温度分析

坝址区气温年周期变化十分明显，7～8月气温较高，12月～次年3月气温较低。极端最高气温为32.1℃，最低气温为-42.5℃，气温变幅较大，多年平均气温为7.1℃。水库大坝301.00m高程以上受气温影响明显，与气温变化有明显的同步性，随着水深增加，水温受气温周期变化的影响逐步减小。

2.2 变形监测分析

由于恒仁水库大坝的视准线观测频度为两个月一次，不具有显著的代表性，因此只对引张线进行分析。引张线布置于坝顶轴线下方0+10.0m处，共设置10个观测点，编号分别为EX1-EX10，本文仅对其中的EX5观测点进行分析。从2008年10月21日以来的引张线自动化监测结果来看，坝顶顺河向水平位移主要受气温周期性变化影响，温度降低向下游位移，并于升高则相反。特别是7～8月水位最高时，大坝坝顶向下游的位移量最小，因此大坝水平位移受水位因素的影响较小。

3 大坝水平位移监测混合模型

3.1 混合模型的优势

目前应用于大坝位移监测领域主要是统计模型和确定性模型[3]。其中，统计模型的优势在于模型构建比较方便，同时还可获得较高的精度和拟合度。统计模型的不足之处在于不能从力学角度解释各分量的对效应量的影响，同时各分量之间也不是随机变量关系，一旦遇到突发情况，统计关系就不适用了。确定性模型是基于工程力学，通过计算环境量与效应量之间的关系构建的具有因果关联性的模型，可以很好弥补统计模型的不足，但是确定型模型的应用需要完整的工程资料，并需要大量的数学计算。

为了弥补上述两种模型的不足，尽量发挥其优势，以上述两种模型为基础构建混合模型，对温度和时效分量采用统计模型拟合，而对应力分量则采用确定性模型进行分析计算，无疑更具有实用价值。

3.2 混合模型的构建

根据现有的理论，水工构筑物运行过长中产生的位移主要与压力载荷、温度载荷和时效变化直接相关[4]。在建模过程中，假定大坝上某点的位移为δ，这个位移可以由空间坐标和诱发的物理因素两种不同方法进行分解，其表达式为：

δ(δx/δy/δz)=δH+δT+δθ

(1)

式中，δ—大坝上某点的位移量；δx—水平位移；δy—侧向位移；δz—竖直位移；δH—水压周期性分量；δT—温度周期性分量；δθ—时效性分量。

3.3 水压分量及有限元计算

在混合模型构建中，水压分量采用基于确定性模型的有限元计算方法。同时，水压分量由库水位分量δH1，扬压力分量δH2和淤沙压力分量δH3三部分组成。

3.3.1 库水位分量

由上述可知，水库大坝上某点的水平位移δH1可以表示为：

δH1=δ1H+δ2H+δ3H

(2)

由于恒仁水库大坝为混凝土重力坝，根据相关文献和有限元计算结果可得：δH1与上游水深H以及H2、H3的多项式之间是正比关系，其表达式如下：

(3)

式中，a—待定回归系数；H—上游水深。

3.3.2 扬压力分量

扬压力分量包括坝基扬压力和坝身扬压力[5]。根据相关文献和工程力学计算，坝基扬压力的计算公式为：

(4)

式中，δH2f—坝基扬压力；hd—坝高；Ec—坝体砼的弹性模量；m—下游坝面坡度；d—观测点距坝顶的竖直距离；H—上游水深。

坝身扬压力对大坝水平位移的影响主要与上下游的水头差线性相关，其表达式为：

(5)

式中,变量的含义同上。

3.3.3 淤沙压力分量

由于泥沙淤积对大坝水平位移的作用比较复杂，同时这种作用还会随着泥沙的不断淤积而变化，因此这种影响作用并不能通过简单的数学参数予以表达[6]。考虑到其影响不能忽略不计，因此在建模过程中将其视为时效因子考虑。

3.3.4 有限元计算

根据上述计算公式，对有限元计算中的坝基和坝体相关参数假定见表1。

表1 大坝不同部位力学参数假定数值

计算过程中的下游水位区平均值248.8m。上游水位选择包括最高水位、最低水位、设计和校核水位的原则，选取304m、301m、299m、297m、295m、293m、291m、289m、287m，共9组水位进行计算。

选择EX5所在的坝体段为整体建立有限元模型。其研究边界为上游2倍坝高，下游1.5倍坝高，竖直1.5倍坝高。坝体两侧为自由边界，基岩两侧限制轴向运动，基岩上下游面施加水流方向约束，基岩底部三向固定约束。整个模型划分为23716个节点，22171个单元。

利用有限元模型计算不同上游水位条件下坝顶的水平位移量见表2。

表2 不同上游水位条件下EX5段坝顶位移计算结果

将上述表格中的数据进行拟合，并引入坝体混凝土平均弹性模量的的修正系数X后，获得EX5水压分量表达式：

δH=X(28.71-4.265ΔH2+25.103ΔH3)

(6)

3.4 混合模型表达式

3.4.1 温度分量

由于恒仁水库大坝监测只设置了六个温度监测点，且其中三个监测点由于温度计不能正常工作而没有完整的监测资料，因此温度资料极为缺乏，不便于采用有限元模型计算，只能采用统计模型进行拟合。鉴于多温度模型的拟合效果明显优于但温度模型，故采用多温度模型进行拟合[7]，并得到如下成果：

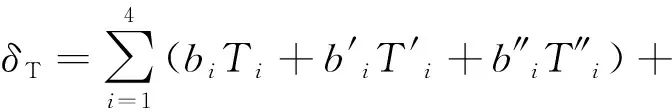
(7)

式中，b—待定回归系数；T—观测日大坝温度；t—距初始观测日的时间，d。

3.4.2 时效分量

时效分量利用统计模型拟合，结果为：

(8)

式中，C1，C2—待定系数；t—距离基准日观测天数。

综合上述成果，可得大坝水平位移的混合模型表达式：

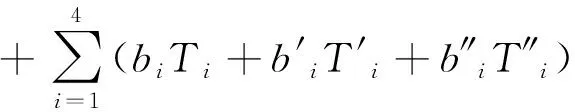
(9)

式中，符号所代表的含义同上。

3.5 模型参数分析

运用SPASS软件进行回归计算[8]，并剔除异常点，获得的各项系数见表3。

由表3的结果可知，上述混合模型的回归方程为：

(10)

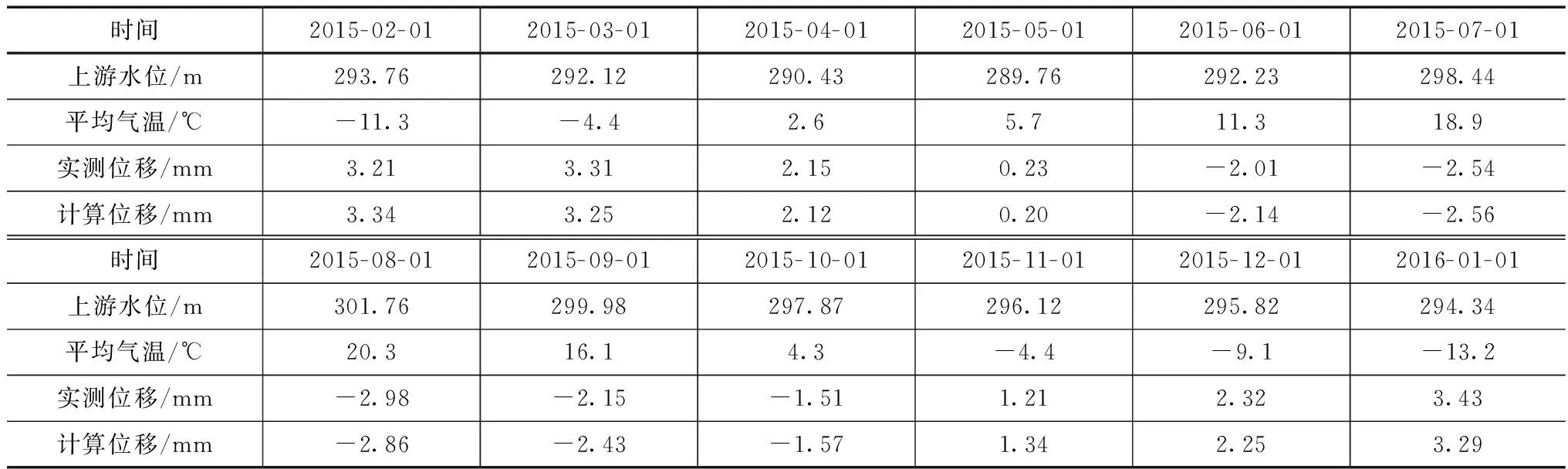
表4 EX5实测值与预测值对比表

注：正值表示向下游偏移，负值表示向上游偏移。

3.6 模型效果分析

通过对2015年2月至2016年1月的实测值和预测值的对比，其中部分数值见表4，可以发现两者具有较好的拟合度，模型的剩余标准差为0.375，能够基本描述发展趋势，具有理想的预测效果。因此，混合模型兼具统计模型和确定性模型的优势，具有一定的实际用用价值。

4 结语

通过人为的、定期的、科学的大坝监测，不仅可以实现对大坝现实安全性实施监控，还有利于对安全隐患未爆发时采取必要的工程措施，具有重要的实际应用价值。我国的许多大坝建于20世纪50，60年代，运行时间已经达到50年以上，运营管理单位急需对大坝进行各方面的监测，持续关注其运行状态。本文基于对恒仁水库大坝的监测研究，提出了具有一定精确度，便于操作的大坝水平位移混合模型，对大坝运行管理者及时判断大坝的运行状况具有重要帮助。但是，研究模型仍然存在待定系数多、计算量大的问题，今后需要在此方面进行深入研究。