例说竞赛题不同思路的比较

何文明 马增山

(邯郸市第一中学，河北 邯郸 056002)

笔者长期从事物理竞赛培训工作,经过多年不懈的努力,每个赛季均有稍许的收获．例如,2017年11月份在重庆举行的第34届物理竞赛决赛中,有两名学生获得金牌,其中一名学生顺利晋级国家集训队．追思已往竞赛培训生涯,给笔者留下深刻印象的,是学生们对崇高目标的追求、坚韧不拔的毅力以及令人惊奇的才思．他们聪慧的头脑经常出乎意料,针对定解问题,突破已有的模式,给出自己独到的见解．本文选取两道经典的竞赛题与读者共享．为了比对,先摘录原题的标准解答,再给出笔者学生的奇思妙想．

题1.(第21届决赛第4题)由如图1所示的电路,其中E为内阻可以忽略的电源的电动势,R为电阻的阻值;S为开关;A、B是如图1所标的8个完全相同的电容均为C的理想电容器组成的电路,问从合上S到各电容器充电完毕,电阻R上发热消耗的能量是多少?(在解题时,要求在图上标出你所设定的各个电容器极板上电荷的正负)

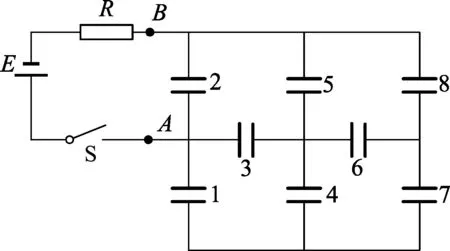
图1

原解析:A、B右边8个电容器组成的电路(图2)可视为一个等效电容CAB,整个电路可简化为图3.下面首先计算等效电容CAB．设合上S到充电完毕的过程中,从A、B两点充入A、B右边电路的电荷量为Q,A正B负．设第i个电容器所充的电荷量为qi,各电容器极板上电荷的正负如图2所示．

根据各节点的电荷守恒可列出下列4个独立方程.

q1+q2+q3=Q，

-q1+q4+q7=0，

-q3-q4+q5+q6=0，

-q6-q7+q8=0.

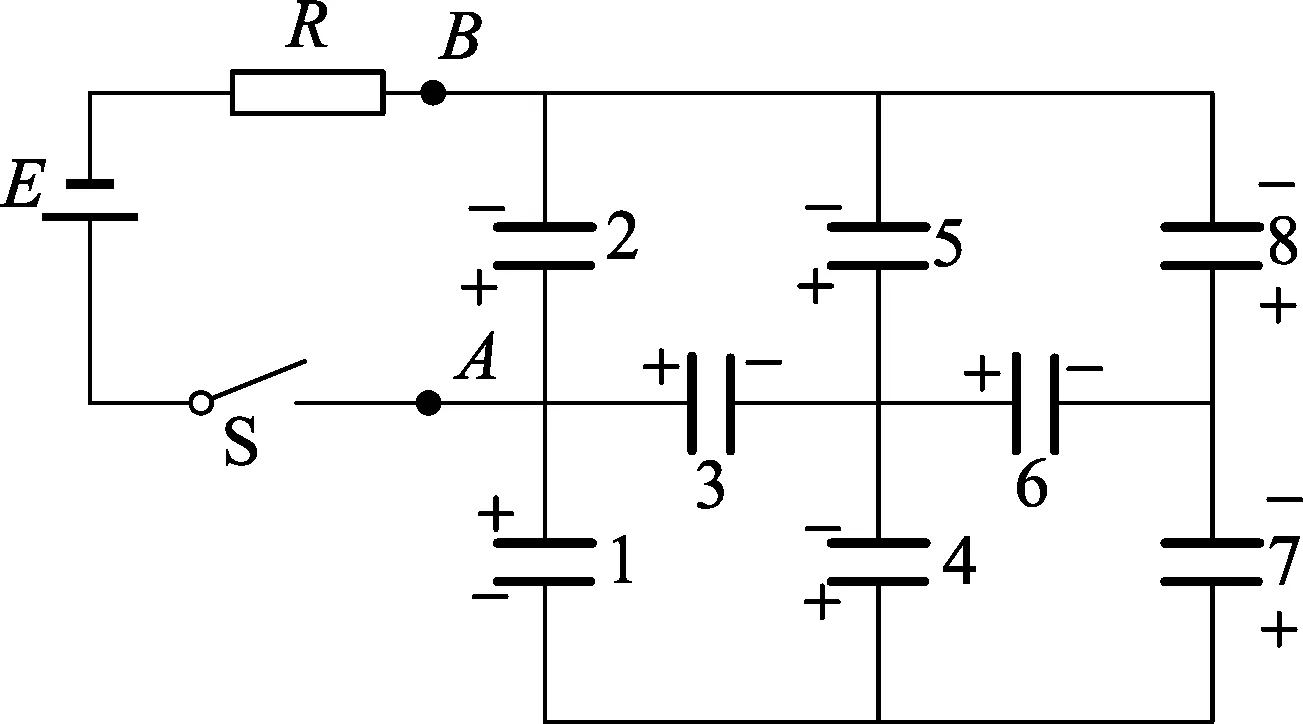
图2 图3

q1+q4-q3=0，

q4+q6-q7=0，

q2-q3-q5=0，

q5-q6-q8=0.

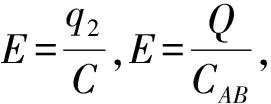
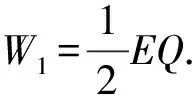
根据能量守恒定律,电阻发热消耗的能量为

W2=W0-W1.

难题巧解:对称性分析．在原电路中取出A、B两点右侧部分电路,电容2直接并联在A、B两点,可暂时去掉不考虑,只对剩余部分进行几何形状的转换,如图4所示．

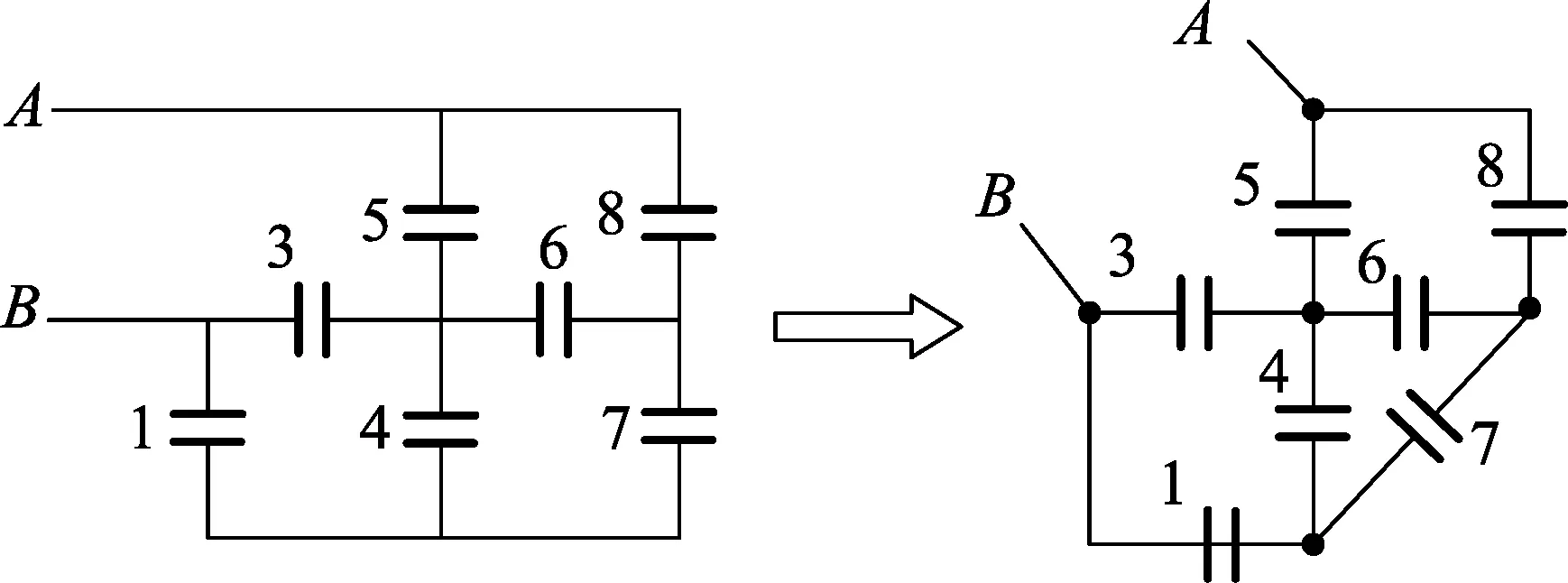
图4

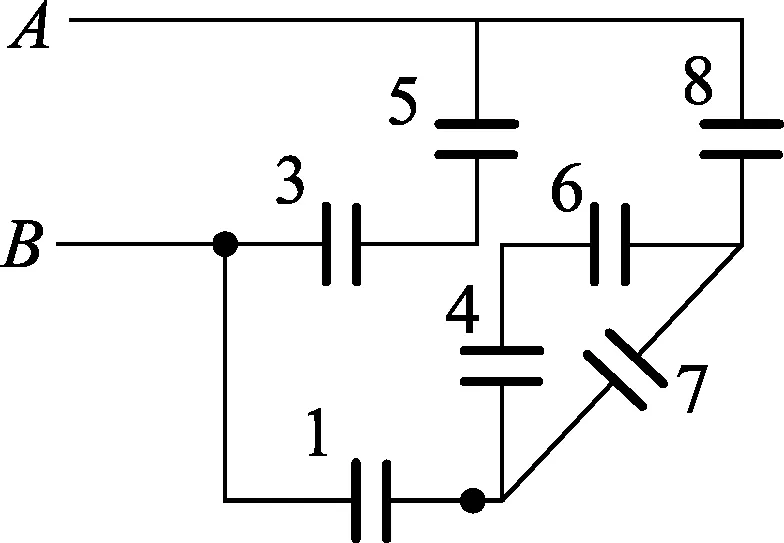
图5

由图4可看出,相对A、B两点,电容网络具有很强的几何对称性:电容1对应电容8,电容3对应电容5,电容4对应电容6,电容7跨接在两个对称点上．这样可以将3、4、5、6之间的连接点断开,成为一个简单的电容串并联网络,成为图5.

点评:这道题的电路结构,以A、B为界限,左边很简单,仅有一个电源E一个定值电阻R;右边是一个“田”字型电容网络．显然,若右边改为一个电容,整个电路就成为电磁学中常见的电容充电电路模型．若如此,无论是求电源充电做功,电容储能,还是电阻生热,对竞赛生来说,易如反掌．但命题者独具匠心地把单个电容改换为复杂的电容网络,这样,这道题难度直线上升,难倒一大批考生．简化这种电容网络有两种方法:一种是设定好每个电容的正负极、电荷量,利用节点电荷量方程和回路电压方程,解出每个电容上的电荷量分布,再进一步根据电压、电荷量的关系求出等效电容,如原解析．显然这种方法想到容易,但8个方程的求解极易出错,无疑增加了解题的难度．第2种方法是根据电容网络特征,找到对称点,经过扭转、变形、拆分、合并等手段,把复杂电路简化成简单的串并联电路,如难题巧解．需要强调的是,对电路对称性分析是解决复杂电容(或电阻)网络的一项基本功,这种技能的提高只能源于解题训练与分析，多观察、多思考,勤于动手改画电路,培养敏锐的科学思维能力,才能在考场上出奇制胜,稳操胜券．

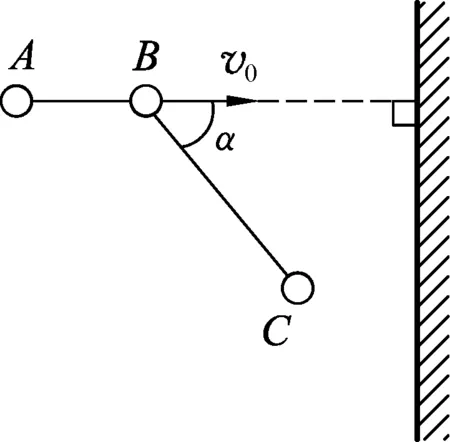
图6

题2.(29届复赛第3题)如图6所示,两根刚性轻杆AB和BC在B段牢固粘接在一起,AB延长线与BC的夹角α为锐角,杆BC长为l,杆AB长为lcosα．在杆的A、B和C3点各固连一质量均为m的小球,构成一刚性系统．整个系统放在光滑水平桌面上,桌面上有一固定的光滑竖直挡板,杆AB延长线与挡板垂直．现使该系统以大小为v0、方向沿AB的速度向挡板平动．在某时刻,小球C与挡板碰撞,碰撞结束时球C在垂直于挡板方向的分速度为0,且球C与挡板不粘连．若使球C碰撞后,球A先于球B与挡板相碰,求夹角α应满足的条件．

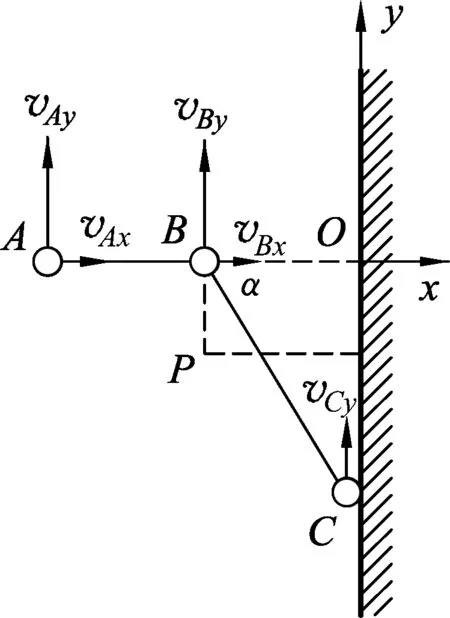
图7

原解析:如图7所示,建直角坐标系Oxy,x轴与挡板垂直,y轴与挡板重合,以vAx、vAy、vBx、vBy、vCx和vCy分别表示球C与挡板刚碰撞后A、B和C3球速度的分量,根据题意有vCx=0，用J表示挡板作用于球C的冲量的大小,其方向沿x轴的负方向,根据质点组的动量定理有

-J=mvAx+mvBx-3mv0，

0=mvAy+mvBy+mvCy.

以坐标原点O为参考点,根据质点组的角动量定理有

Jlsinα=mvAy(lcosα+lcosα)+mvBylcosα+mv0lsinα.

因为连结小球的杆都是刚性的,故小球沿连结杆的速度分量相等,故有vAx=vBx，

vCysinα=vBysinα-vBxcosα，

vAxcosθ-vAysinθ=-vCysinθ.

上式中θ为杆AB与连线AC的夹角.由几何关系有

联系以上各式得

J=mv0(1+2cos2α)，vAx=v0sin2α，

vAy=v0sinαcosα，

vBx=v0sin2α，vBy=0，vCy=-v0sinαcosα.

按题意,自球C与挡板碰撞结束到球A(也可能球B)碰撞挡板墙前,整个系统不受外力作用,系统的质心做匀速直线运动.若以质心为参考系,则相对质心参考系,质心是静止不动的,A、B和C三球构成的刚性系统相对质心的运动是绕质心的转动.为了求出转动角速度,可考察球B相对质心的速度.由上面有关各式,在球C与挡板碰撞刚结束时系统质心P的速度为

这时系统质心的坐标为

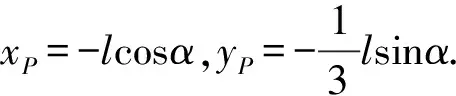
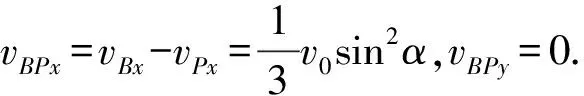
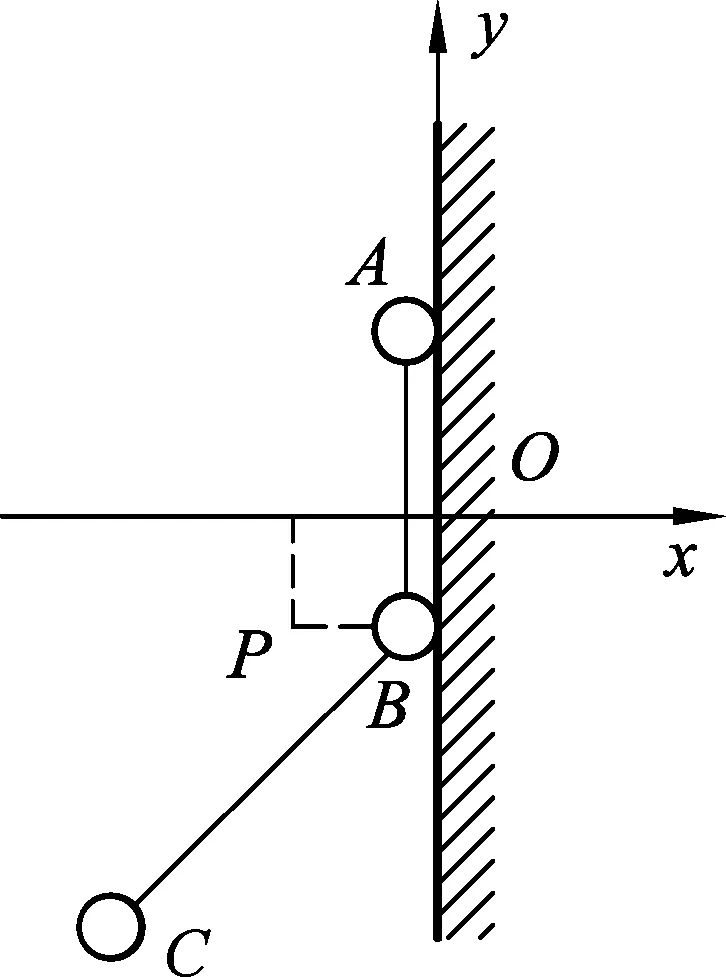
图8

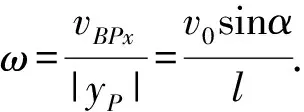
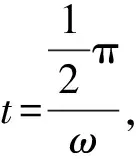
这道复赛题,从所给的标准答案看,是很繁的．要做好这道题,学生需对牛顿力学的动量、角动量、质心、刚体系速度关系等知识点了然于胸,同时还必须有很强的计算能力．试卷注明这道题分值是25分,(从34届开始,所有复赛题和决赛题分值加倍,当年的25分折合成现在就是50分．)也充分说明本题属于难题等级．然而,就是这样一道难题,笔者的一位学生却轻松地给出了自己的解答,其简捷程度令人拍案叫绝．现在欣赏其解析.

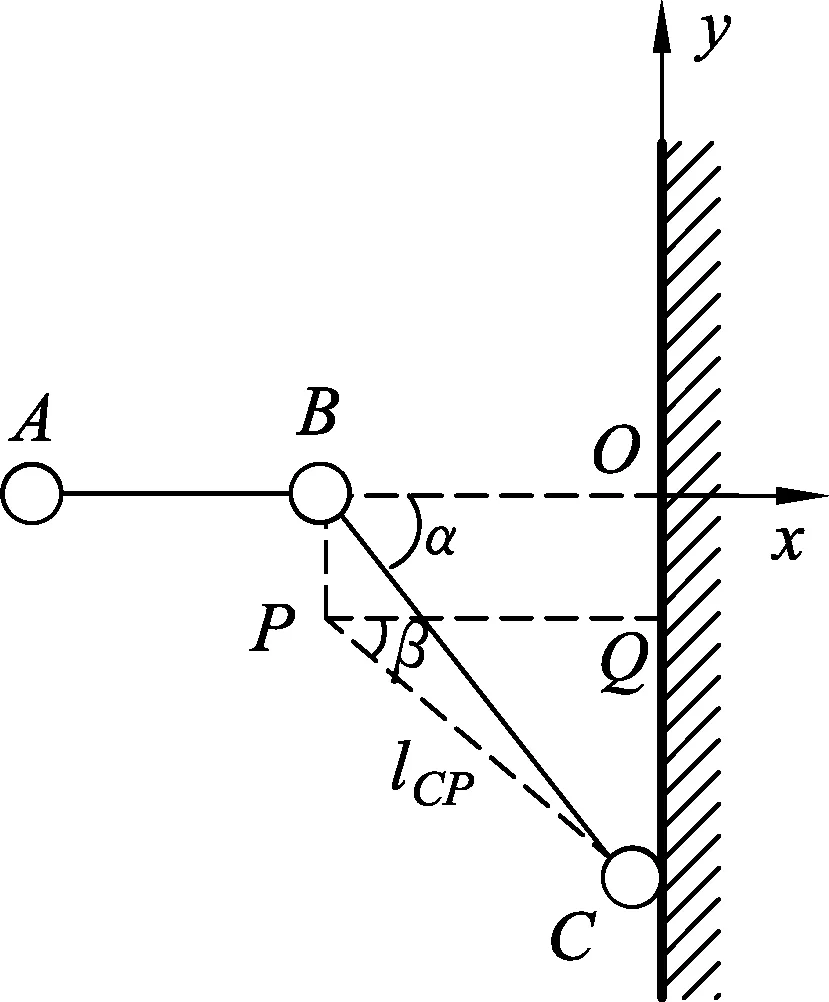
图9

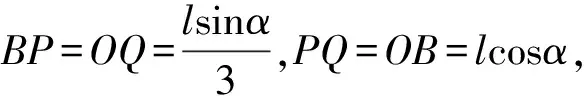
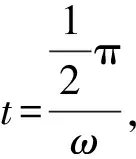
点评:从难题巧解看,满足题目要求的夹角α并不依赖质心速度大小,因此在球C碰墙后,只要赋予质心任意大小的速度都可解出α>36°,这恐怕是命题教师没有意料到的．这说明,对所求结论而言,原解析中前面大段的动量、角动量、刚体运动等等计算都是无效的劳动．为了不降低这道题的难度,并且达到良好的选拔功能,可以把设问变通一下,例如先求碰后三球的速度,再求角度α满足的条件,这样就避免了上述尴尬,也成就了一道经典好题．