一类动力学极值问题的几何解法

张子云

(江苏省苏州第十中学校，江苏 苏州 215006)

高中数学知识的教学进度往往落后于高中物理教学的需求．物理教师在讲解一个数学知识点的时候也只是重在应用，而很少介绍数学结论的由来.这对于我们习得此数学知识不利,甚至对应用到该数学知识的物理规律本身也会产生消极影响．

在解决一类动力学极值问题时,笔者发现当涉及到其中有一对接触面之间同时存在正压力和滑动摩擦力的多力(超过3力)求满足一定条件的极值问题,除了可以采用代数法求解外,还可以采用几何方法求解．

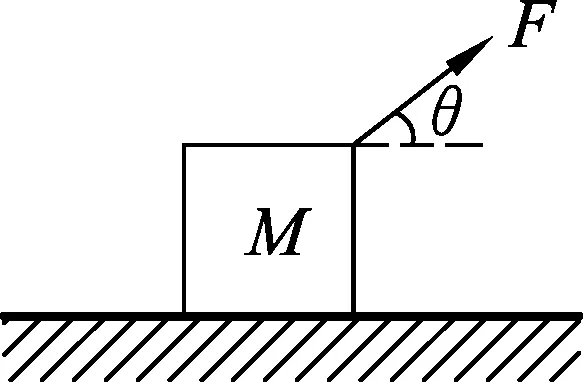
图1

例1.如图1所示,水平地面上静止放有一质量为M的物体,物体与水平地面间的动摩擦因数为μ,用一恒力F作用在此物体上使其在水平地面上匀速运动的最小恒力F为多大,与水平方向夹角如何?

本题的常规解法如下.

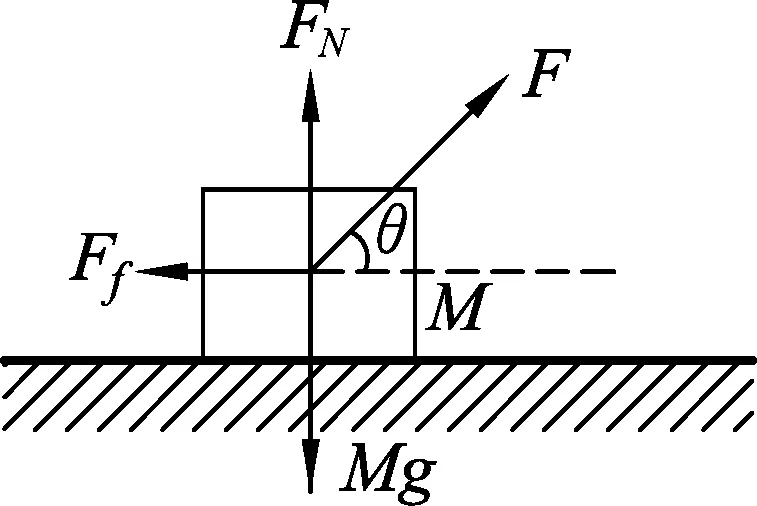
图2

物体受重力Mg、拉力F及水平地面的支持力FN、滑动摩擦力Ff，见图2．

选择水平向右方向为x轴正向、竖直向上为y轴正向,将拉力F分解到水平、竖直方向,由于物体做匀速运动,因此两方向都受力平衡．

水平方向有

Fcosθ-Ff=0，

(1)

竖直方向有

Fsinθ+FN=Mg.

(2)

同时

Ff=μFN.

(3)

联立(1)～(3)式得到

(4)

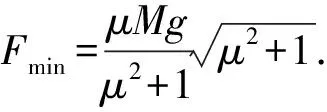
在一次物理课上老师介绍利用三角形法则来进行矢量运算,对于求动态过程中的极值很方便后,笔者在课余不仅想到能否利用三角形法则来解例1呢?在得到老师的肯定后,利用课余时间进行了尝试,取得了成功．

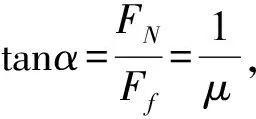
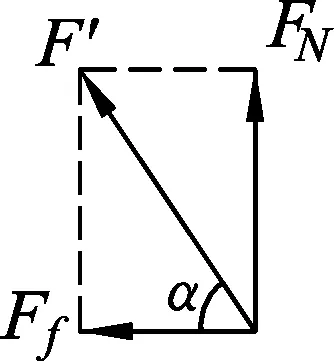
图3

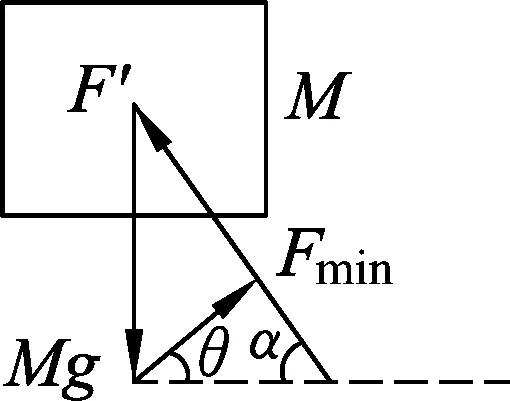
图4

显然,几何解法比前面的常规方法简单,而且更直观、更好理解.

而对于物体具有确定加速度的非平衡态,类似的情况也能用几何方法求解．

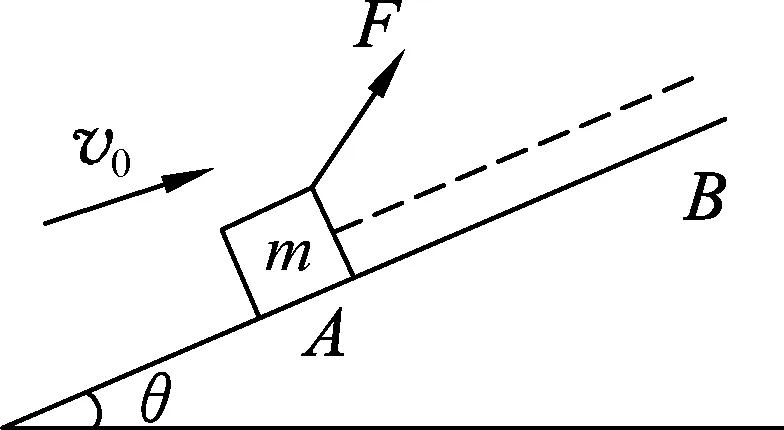
图5

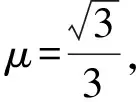
(1) 求物块加速度的大小及到达B点时速度大小．

(2) 拉力F与斜面的夹角多大时,拉力F值最小?最小值是多少?

在参考答案中,该题给出的解法也是利用三角函数极值公式,这里不再赘述．

根据运动学公式可知，物块加速度a=3m/s2．本文此处着重介绍第(2)小题的几何解法．

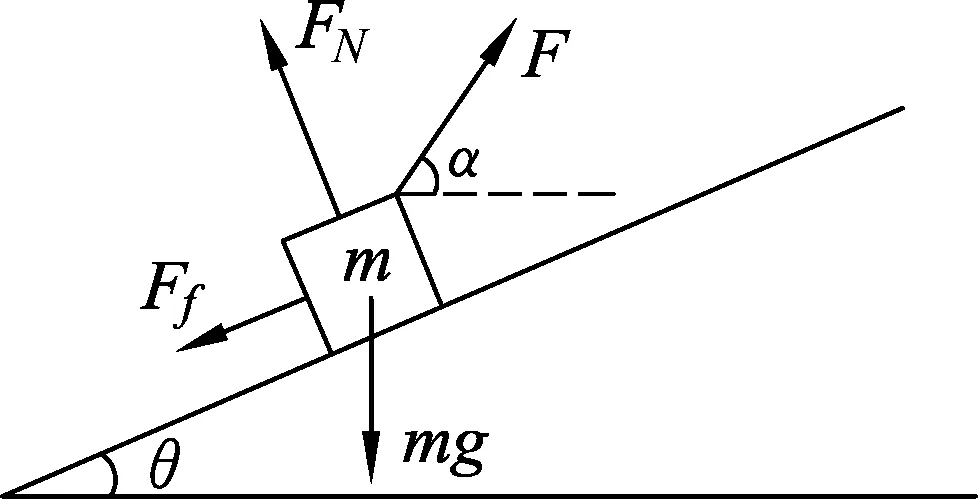
图6

设物块所受斜面作用的支持力为FN、滑动摩擦力为Ff,同时物块受重力mg,及与水平方向成α角的拉力F作用,如图6所示．

此处两力同样满足固定的数值关系,因此先将此两力看做一个力F′,其大小不定但方向确定．物块受到等效力F′、重力mg、拉力F3力作用的最终合力为沿斜面向上的F合=ma．

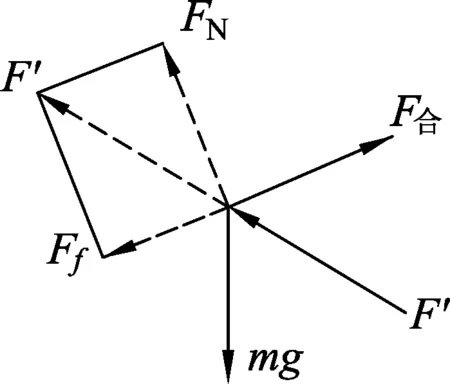
图7

为便于画图,这里用一个点代表物块,将所有的力作用在该点上，见图7．

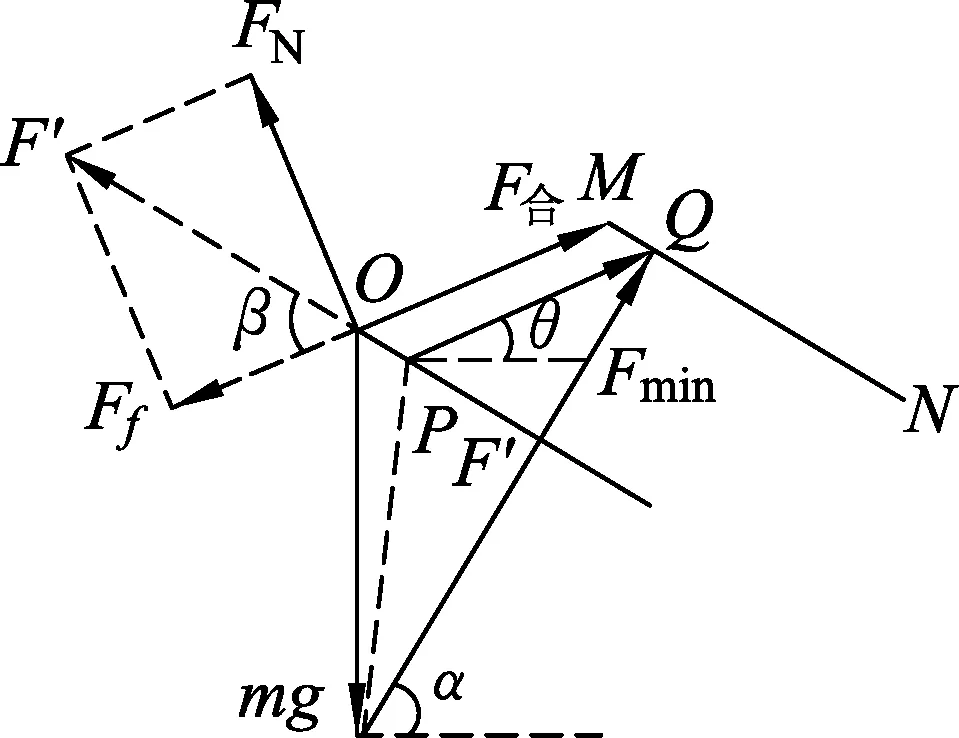
图8

接下来,此处需要考虑的问题变成了在重力mg大小方向已知、另外一个力F′方向确定大小可变,再找一个最小的拉力F,使3力合力为F合．由于F大小方向都未知,所以先考虑将重力mg和F′先合成，它们的合力一定起点位于F′上,终点为mg的终点,记作F″．力F″与所求F(记作Fmin)的合力为F合,于是应该将F″、Fmin首尾相连．取mg的终点为Fmin的起点,过图8中F合的终点作F′的平行线MN,过mg的终点作MN的垂线段,垂足为Q,此即为所求Fmin．将F合终点平移至落在Q点上,与F′交点记作P,PO即为实际的F′，如图8所示．

从上述两个例题可以看出,几何法解题的优点在于直观．由此可见,在处理复杂的物理问题时,抽象性往往是思维过程中的最大障碍,而通过几何图像将抽象问题具体化、直观化,可以提供有效帮助．因此,在学习物理过程中,养成尽量画图、帮助思考的好习惯是很有必要的．