限制空间范围条件下(类)平抛运动的末速度极值问题举例
李爱华
(华中师大一附中,湖北 武汉 430223)
平抛运动是一种重要的匀变速曲线运动,如果在运动中加上平面、曲面等不同限制空间范围的条件,其末速度、时间、位移等物理量呈现出非单调变化,使之成为考查学生物理基本技能、运用数学知识解决物理问题的高考的热点.
1 竖直面对抛体运动的限制
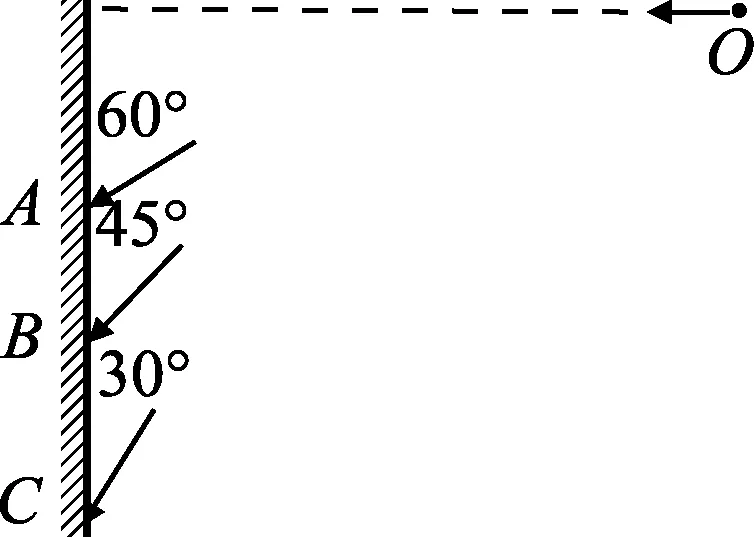
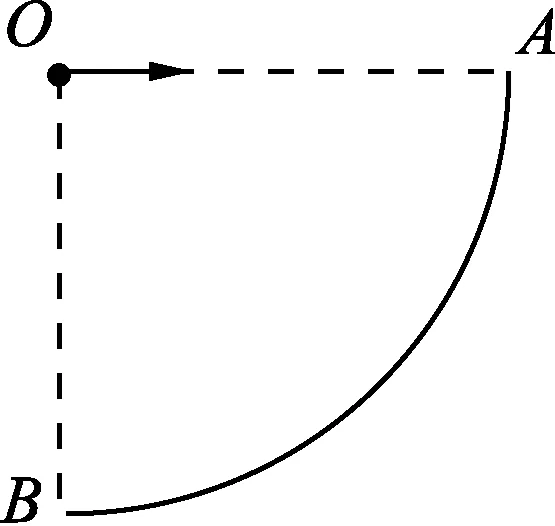
图1
例1.如图1所示,某人从同一位置O以不同的水平速度投出3枚飞镖A、B、C,最后都插在竖直墙壁上,它们与墙面的夹角分别为60°、45°、30°,图中飞镖的取向可认为是击中墙面时的速度方向,不计空气阻力,则下列说法正确的是
(A) 3只飞镖做平抛运动的初速度一定满足vA0>vB0>vC0.
(B) 插在墙上的3只飞镖的反向延长线一定交于同一点.
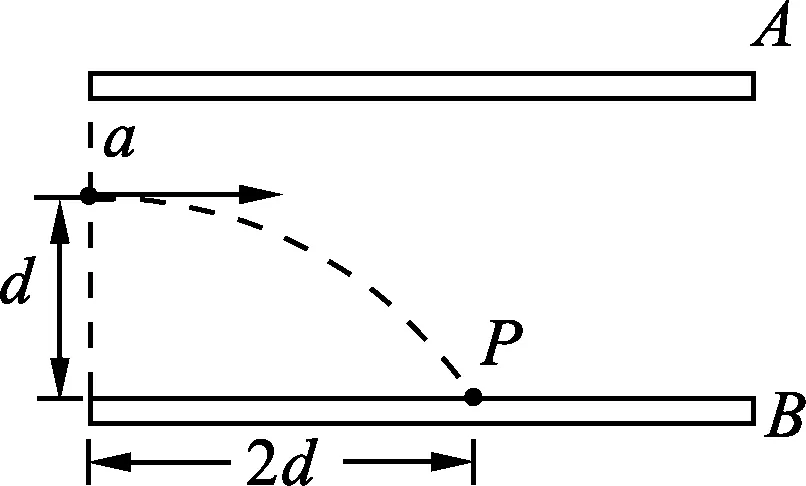
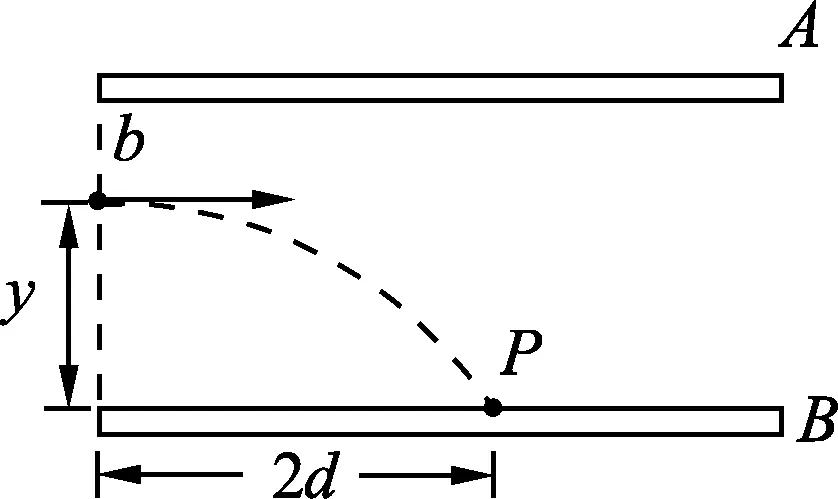
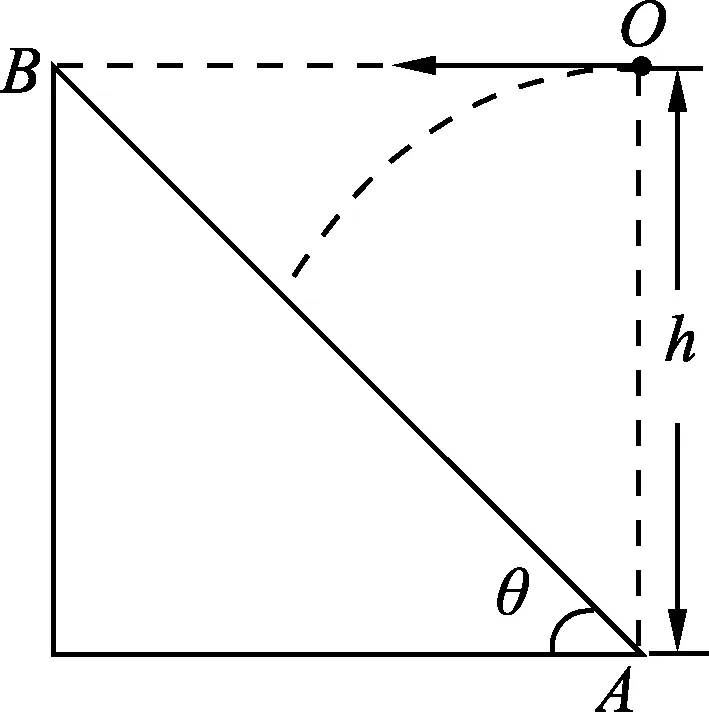
(C) 3只飞镖击中墙面的速度满足vA (D) 3只飞镖击中墙面的速度一定满足vA=vC>vB. 图2 解析:答案为(A)、(B)、(D).对于(D)选项,如图2所示,考虑写出飞镖打在墙面某点E的末速度v关于θ的函数. 设OD为x,DE为y,由平抛运动规律 以上各式联立得 启示:(1) 从定点O到竖直约束面,水平位移x一定,考虑用x表示其他物理量. (2) 直接区别A、B、C3点的是飞镖与墙面的夹角,所以优先考虑写出末速度v关于θ的函数. (3) 本例用到求极值方法1——三角函数求极值. 图3 例2.如图3所示,水平放置的平行板电容器极板A、B间加有恒定电压,a点与下极板的距离为d,一带电粒子从a点水平射入电场,初速度大小为v1,粒子偏转后打在下极板的P点时速度大小为v1′,其水平射程为2d.若该粒子从与a点在同一竖直线上的b点(图中未标出)水平射入电场,初速度大小为v2,带电粒子仍能打到P点,打到P点时速度大小为v2′.下列判断正确的是 (A) 若b点在a点上方,则v1>v2. (B) 若b点在a点下方,则v1>v2. 图4 (C) 若b点在a点上方,则v1′>v2′. (D) 若b点在a点下方,则v1′>v2′. 解析:答案为(A)、(B)、(D).对于(B)、(D)选项,如图4所示,设初速度为v,加速度为a,打到P点电场方向位移为y,由类平抛运动规律及动能定理 以上各式联立得 启示:(1) 从竖直线到水平面定点P,水平位移x=2d保持一定. (2) 竖直(电场)方向位移y变化,优先考虑写出末速度v关于y的函数. (3) 本例用到求极值方法2——双勾函数求极值. 图5 例3.如图5所示,一质量为m的质点从倾角θ=45°的底端正上方h=2.4m处水平抛出,不计空气阻力 (B) 若初速度加倍,小球飞行时间减半. (C) 若小球垂直撞在斜面上,则初速度为4m/s. (D) 若落点由A到B逐渐升高,小球落到斜面时的动能逐渐增大. 解析:答案为(A)、(C)、(D).对于(D)选项,设小球初速度为v0,落到斜面上时,下落的高度为y,水平位移为x,由平抛运动规律及动能定理 注意到斜面约束 联立得 (2) 本例用到求极值方法2——双勾函数求极值. 图6 (1) 求此人落到坡面时的动能; (2) 此人水平跳出的速度为多大时,他落在坡面时的动能最小?动能的最小值为多少? 解析:(1) 设探险队员跳到坡面上时水平位移为x,竖直位移为H,由 此过程中由动能定理,得 注意到抛物面约束 和几何关系 y=2h-H. 联立得 启示:(1) 可以考虑在题设坐标系下直接写出探险队员的抛物线方程,求出两条抛物线交点,辅以能量关系写出末动能关于初速度的函数. (2) 本例用到求极值方法3——基本不等式性质,求极值方法4——配方法求极值. 图7 例5.如图7所示,AB为竖直平面内1/4圆弧,可视为质点的小球从圆心O处水平抛出,不计空气阻力,当小球落到圆弧上时 (A) 落点越靠近B点,平抛运动时间越长. (B) 速度的反向延长线可能过OA的中点. (C) 小球落在圆弧中点处时动能最小. (D) 动能最小的位置在圆弧中点的下方. 解析:答案为(A)、(D).设小球初速度为v0,落到圆弧上时,下落的高度为y,水平位移为x, 圆弧半径为R,由平抛运动规律 此过程中由动能定理,可得 注意到弧面约束 x2+y2=R2. 联立得 启示: (1) 从定点O到圆弧面,合位移大小恒为R,可考虑用x表示y,也可考虑优先用角度参量θ表示为x=Rcosθy=Rsinθ. (2) 本例用到求极值方法2——双勾函数求极值,也可用三角函数求极值. 解决此类问题,要充分注意限制条件对水平位移、竖直位移或合位移的限制,抓住不变的量,写出相应函数关系式,灵活运用三角函数、双勾函数、基本不等式性质、配方等相关数学知识求解.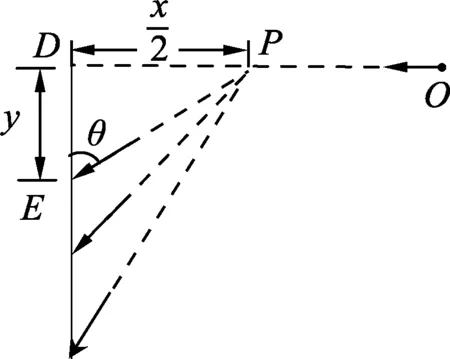
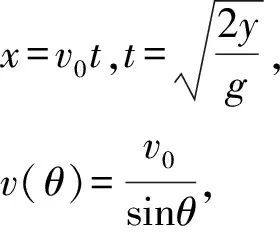
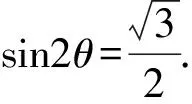
2 水平面对抛体运动的限制
3 斜面对抛体运动的限制
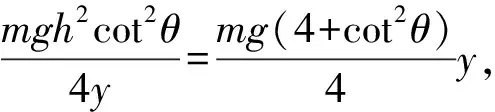
4 抛物面对抛体运动的限制
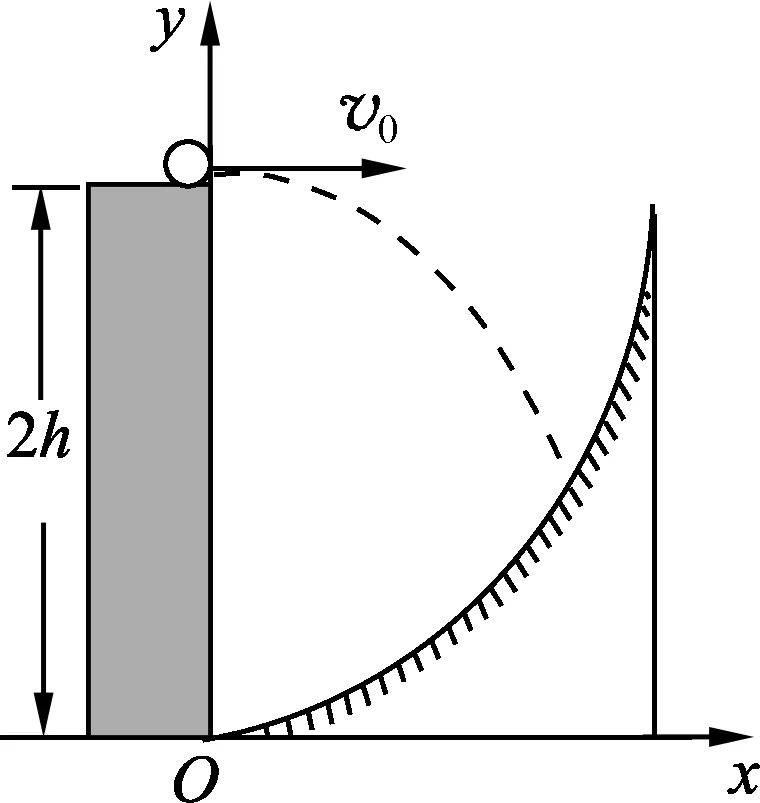
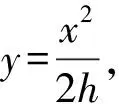
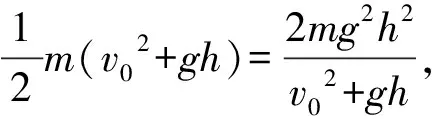
5 圆弧面对抛体运动的限制