最大最小目标的多旅行商问题求解①

袁 志

(广州大学 华软软件学院, 广州 510990)

1 概述

多旅行问题(Multiple Traveling Salesmen Problem,MTSP)是TSP的扩展. 给定一个中心城市和n个访问城市, 将访问城市分配给m个旅行商, 每个旅行商从中心城市出发巡游若干访问城市后回到中心城市, 要求所有旅行商经过的总路程(total)尽量小且其中最长环路的长度(max)尽量小. 事实上, 无法保证total和max两个目标同时达到最小, 本文寻求最小化max, 称之为MinMax-MTSP. 这一类问题的算法可应用在工作均衡调度, 印刷机调度、卫星测量系统设计、机器人应急响应[1–3]等领域.

城市集合C ={c0,c1,c2,…,cn}, c0表示中心城市, c1,c2,…,cn表示访问城市. 距离矩阵D={di,j}, di,j为ci到cj的距离. 每条环路用城市号序列来编码, 例如cycle =(0,1,2)表示 c0→c1→c2→c0. 图1显示了 n=10, m=3 的MinMax-MTSP的一个解(非最优解), 其中的3条环路分别是(0,1,2), (0,5,4,3)和(0,6,7,8,9,10), 解表示为S=(0,1,2,0,5,3,4,0,6,7,8,9,10). MinMax-MTSP求解目标是寻找S的最佳序, 使max最小.

将进化算法与局部搜索算法结合来求解MTSP是近年来的主要方法. 一类是遗传算法, Carter[4]提出了一种双基因编码(城市基因和组基因)的遗传算法, 并提出了12个测试例; Brown[5]提出一种分组遗传算法.Yuan[6]在分组遗传算法中引入了一种新的交叉算子(TCX), 提出了3个新的测试例; Singh[7]改进了分组遗传算法(GGA-SS), 用组的rk值(rk=路径长度/城市数)衡量一个组属于最优解的可能性, rk值较大的组优先保留在子代中, 其余一些零散的城市用贪心算法插入到各个组, 使用2-opt局部搜索算子进行组内优化.另一类是群体智能算法, Liu[8]用蚁群算法求解MTSP;VENKATESH[9]提出了两种蜂群算法(ABCFC、ABCVC) 和一种杂草入侵算法 (IWO), 同样用2-opt进行组内优化.

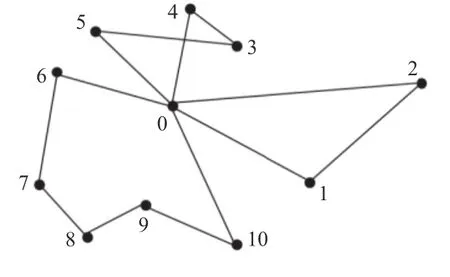
图1 3个旅行商10个访问城市的一个解

以上算法的一致性在于: 使用局部搜索算法来快速加速寻优过程, 使用群体进化算法不断累计优化结果. 这些算法采用2-opt作为局部搜索算子, 而且仅将2-opt作用于单条环路的优化. 实际上, 在MTSP中, 可以将局部搜索从单条环路的优化扩展为两条环路的重组优化, 加速算法的寻优过程(第2节讨论). 这些算法主要依赖个体之间交换信息来完成迭代优化, 很少考虑到局部搜索算子自身的特点, 在进化算法中根据局部搜索算子自身的特点, 设计新的进化机制, 是本文关注的另一个重要内容(在第3节讨论).

本文设计了一个新的局部搜索算子reverse/ move(转置/移动), 该算子既能进行一条环路的优化, 也能重组优化两条环路, 即便在一条环路上进行优化, 其能力也明显好于2-opt; 在分析reverse/move算子特点的基础上, 提出了“搜索-选优-变异-搜索”策略, 设计了竞争搜索算法(Competitive Search Algorithm, CSA), 在文献[4]和文献[6]的15个测试例上进行实验, 与文献[6–9]进行比较, CSA在计算结果上有明显的改进.

2 局部搜索算子reverse/move

为了指导搜索过程, 需要对解有合适的评价方法.MinMax-MTSP的目标是最小化max, 但注意到, 将目标改为优先最小化max, 其次最小化total, 有助于最小化max. 因为后者要求每一条环路自身次序最优, 在大多数情况下, 这有利于最小化max.

以图1为例, 算法运行到当前步骤, (0,6,7,8,9,10)是最长环路, 次序已经是最优; (0,5,3,4)是另外一条稍短的环路, 次序不是最优. 此时对(0,5,3,4)进行优化得到(0,3,4,5), 然后从(0,6,7,8,9,10)中移动“6”到(0,3,4,5)可以得到(0,3,4,5,6), 这是一条新的最长环路,而且比前一条最长环路更短.

因此, 将解的适应值设计为一个二元组(max,total), 规定: 解 S1优于解 S2, 当且仅当 (max1＜max2) 或(max1=max2且 total1＜total2).

本文局部搜索算子通过依次检查S中的每一个位置来完成. 下文中, 将被检查位置上的城市标记为c1,它在S中的后一个城市标记为c3, c1的邻域N(c1)中的城市的标记为c2, c4和c5分别是c2在S中的后一个城市和前一个城市. 按照Lin-kernighan算法的建议,N(c1)取离c1最近的6个城市.

我们的局部搜索方法是: 依次检查S的每一个位置, 对于该位置上的城市c1, 对N(c1)中每一个c2, 做两种尝试: 先尝试转置c2与c3之间(包含c2与c3)的次序, 得到 S′, 如果 S′优于 S, 则用 S′代替 S; 否则尝试将c2移动到 c1和 c3之间, 得到 S′, 如果 S′优于 S, 则用S′代替S. S包含n+m个位置, 如果连续检查n+m个位置都无法优化 S, 算子停止. 转置和移动合称“reverse/move”.

c2和c3可能位于S中的同一环路, 也可能位于两条不同的环路, 以下分别进行讨论.

当c2和c3在同一环路中, 转置c2和c3之间的次序将删除两条边并新增两条边, 效果如图2(a), 例如:cycle=(0,1,2,3,4,5,6), c2=1, c3=5, reverse(cycle)=(0,5,4,3,2,1,6); 移动c2将删除三条边并新增三条边, 效果如图2(b), 例如: cycle=(0,1,2,3,4,5,6), c2=1,c3=5, move(cycle)=(0,2,3,4,1,5,6).

当c2和c3属于分属两条环路. 转置c2和c3之间的次序, 将对两条环路进行重组, 效果如图3(a), 例如:S=(0,1,2,0,5,3,4,0,6,7,8,9,10), c2=1, c3=7,reverse(S)=(0,7,6,0,4,3,5,0,2,1,8,9,10). 移动 c2, 相当于将c2从一条环路中移除, 插入到另一条环路, 效果如图3(b), 例如: S=(0,1,2,0,5,3,4,0,6,7,8,9,10), c2=1, c3=7,move(s)=(0,2,0,5,3,4,0,6,1,7,8,9,10).

图2 一条环路中的转置/移动

图3 跨两条环路的转置/移动

我们在经典TSP的公开测试数据TSPLIB上比较reverse/move与2-opt. 经典TSP问题相当于m=1的MTSP问题, 其上的测试结果能够反映局部搜索算子的寻优能力. 对每个测试例, 分别产生800个随机的初始解, 然后各用reverse/move与2-opt两种局部搜索进行优化, 得到800个最终解. 从两个方面进行比较: 1)环路长度(length)的平均值, 2) 检查位置数(checkedpoints)的平均值, 结果如表1.

表1 reverse/move与2-opt的搜索能力比较

表1显示, 对每一个测试例, 两种局部搜索算法在停止时, reverse/move检查的位置数略大于2-opt, 与此同时, 在搜索的结果上, reverse/move的明显好于2-opt.

3 竞争搜索算法

当reverse/move算子停止搜索时, 对所得到的解S, 选择其中一个片段, 转置其次序, 然后再执行reverse/move, 可能得到更优的解. 以图4为例, 图4(a)是reverse/move得到的一个解, 图4(b)是一次转置的结果, 图4(c)和图4(d)是再次执行reverse/move的中间过程和结果.

图4 转置一个片段后再次执行reverse/move

用一对城市号(cstart,cend)来标记S中的一个片段,这样的对共有(n+m)×(n+m-1)/2个, 构成S的候选对集. 用随机方式来选择一对城市, 转置其所标记的片段,然后再次执行reverse/move, 可能有三种结果: 1) 得到更好的解, 2) 恢复到转置之前的解, 3) 得到变差的解.每选出一对城市, 就从S的候选对集中将其删除, 直到候选对集为空.

根据reverse/move的以上特点, 我们提出一种群体迭代策略: “搜索-选优-变异-搜索”, 用图5 说明. 图5中的横坐标是解空间, 纵坐标是解的适应值. 如果一组解经过局部搜索得到相同的局部最优解, 则将这组解集中在一个区域, 该区域中适应值最小的解就是该区域的局部最优解. 选择最好的若干个局部最优解, 对其进行变异(随机的片段转置), 得到的一部分新的解将到达新的区域, 经再次搜索得到新的局部最优解. 如此迭代, 逐步提高局部最优解的质量, 直至最好的若干个局部最优解的候选对集全部为空.

图5 多个解经过局部搜索得到相同的局部最优解

基于这一策略, 我们设计了竞争搜索算法(CSA),如算法1.

算法1. CSA算法1) 设定种群规模p和选择比例θ(θ建议取0.2), 随机生成p个初始解, 对每个解执行reverse/move.2) 对所有解按适应值从小到大排序, 保留θ×p个排名靠前且互异的解.3) 对保留的解, 从其候选对集中随机选(1–θ)/θ个城市对, 并从候选对集中删除这些对; 对保留解, 分别转置这些片段产生新的解.4) 在新的解上执行reverse/move, 然后加入种群.5) 循环执行2)到4), 直至所有保留解的候选集为空.6) 输出群体中的最优解.

CSA算法与保留精英的遗传算法相似, 其特异性在于: 用局部搜索reverse/move取代杂交操作; 用最优且互异的若干个体作为父代个体, 取代概率性选择; 用固定的小尺度变异(转置一个片段)替代概率性变异.

4 实验

我们用文献[4]的12个测试例和文献[6]的3个测试例作为实验数据. 文献[4] 的12个测试例中的城市数据是二维平面坐标, 包括MTSP-51的3个问题(m=3,m=5,m=10), MTSP-100的4个问题(m=3,m=5,m=10,m=20)和MTSP-150的5个问题(m=3,m=5,m=10,m=20,m=30), 用第一个城市作为中心城市. 文献[6]的3个测试例中的数据是128个城市的经纬度和距离矩阵, 包括sgb128(m=10,m=15,m=30), 用第一个城市作为出发城市.

我们在2.8 GHz, 2 Core, 4 G RAM的Windows 8.1系统上实现了CSA, 在实验中种群规模p设置为50. 表2给出了CSA在15个测试例上得到的最小的最长环路长度(best max)、迭代次数(iterations)和计算时间(time).

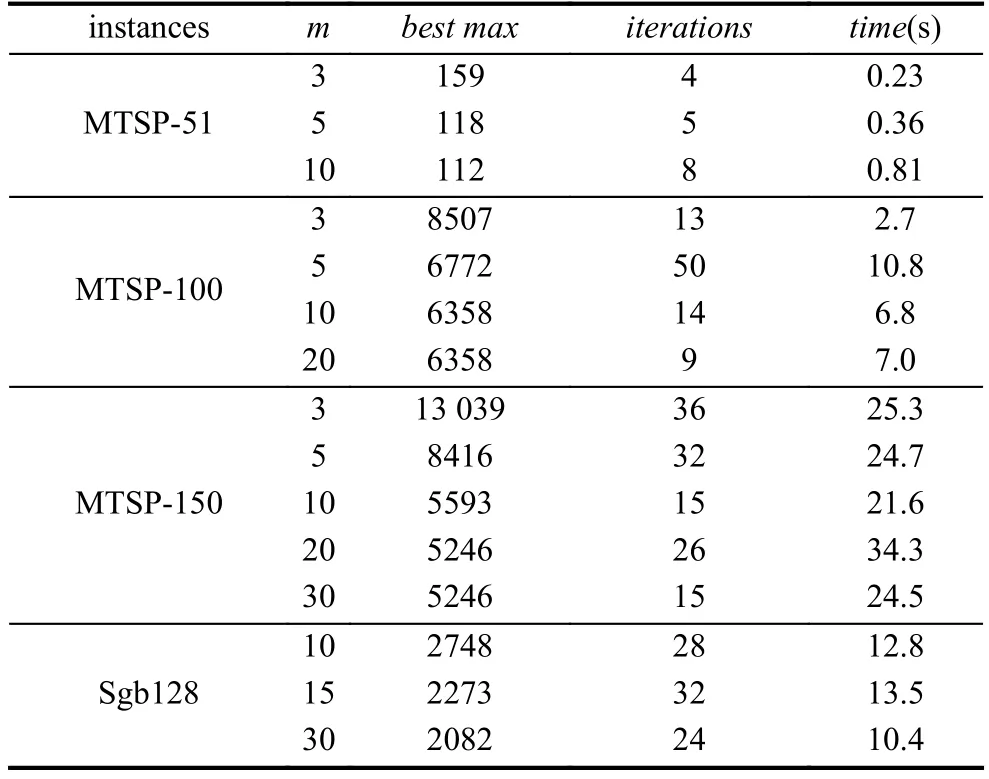
表2 CSA算法的结果、迭代次数和时间

表2说明, CSA能在较短时间内终止, 满足实际应用的需求.

对于文献[4]的12个测试例, CSA所得的best max与文献[6–9]的结果比较如表3.

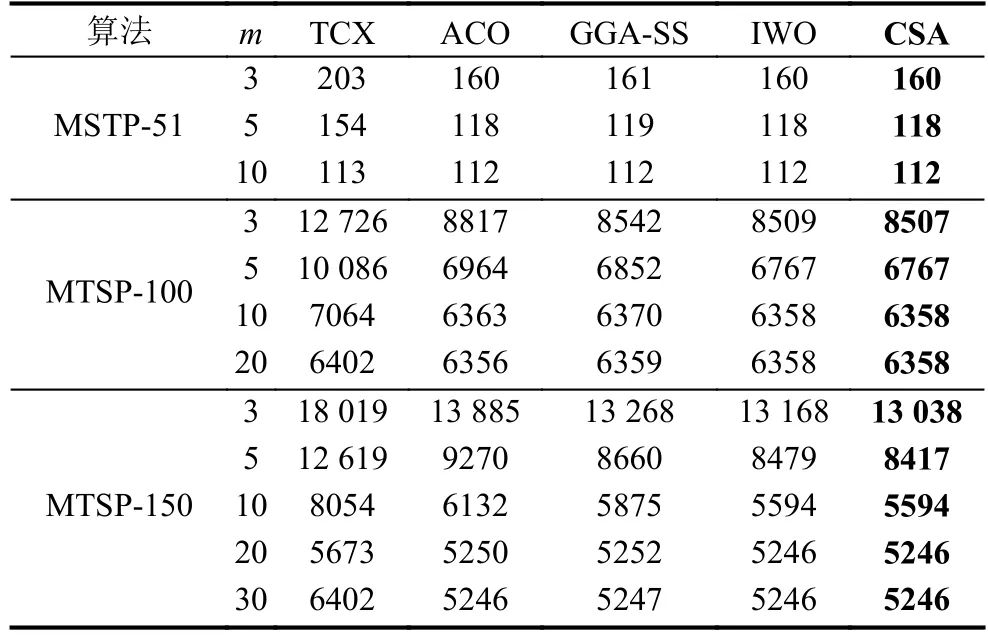
表3 几种算法在文献[4]测试例上的best max比较

由表3, 对文献[4]的12个问题, 在所有算法中,CSA的结果都优于或等于现有算法的最好结果, 其中两个测试例MTSP-150 (m=3,m=5)的解展示在图6中.

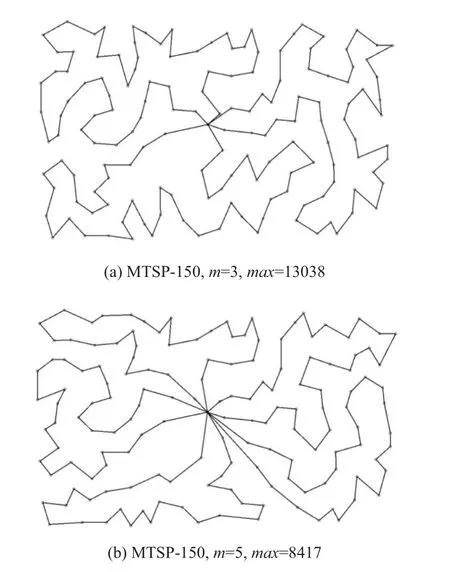
图6 CSA在文献[6]问题上的两个解

对于文献[6]的3个测试例, CSA所得的best max与文献[6–9]的结果比较如表4.

由表4, 对文献[6]的3个测试例, CSA的结果有大幅度改进. 由于文献[6]提供的128城市的坐标用经纬度来表示, 在二维平面较难展示, 下面给出m=10,max=2748的解, 其中每一对括号包含的是一条环路.

表4 几种算法在文献[6]测试例上的best max比较

5 结论

为了求解最大最小目标的多旅行商问题, 在对现有文献进行研究的基础上, 提出了竞争搜索算法(CSA), 与近期文献中的相比, 明显提高了解的质量. 局部搜索算子和变异算子是CSA算法中的两个关键算子. 我们曾采用多种不同的变异算子, 包括: 随机移动一个城市、随机转置一个片段、随机转置两个或多个片段以及这些操作的组合, 我们观察到, 采用不同的变异算子, 在收敛速度和最终解质量上有明显差异, 其中,随机转置一个片段的变异方法明显好于其他方法. 改进变异方法, 可能进一步提高CSA算法性能.