存在站址误差下的无源雷达稀疏成像*

， ， ， ，

(中国卫星海上测控部， 江苏江阴 214431)

0 引言

无源雷达成像是一种利用外辐射源发射的电磁波信号对目标进行成像的双/多基地雷达系统，具有优越的“四抗”性能，一直是雷达界的研究热点。随着通信、导航等技术的发展，空间中的电磁信号种类越来越丰富，目前已被证实可用的外辐射源包括调频广播(FM)[1]、数字地面电视(DVB-T)[2]、全球导航卫星(GNSS)[3]等。然而上述信号不是为雷达系统专门设计，信号带宽通常较窄，带宽对成像分辨率的贡献明显不足，因而基于传统匹配滤波成像方法通常获得的空间分辨率较差[4]。

2004年以来，随着压缩感知理论的提出，可以在较低信号带宽、较低信号采样速率情形下获得较好的成像性能，大大提升了无源雷达成像的应用潜力。因此基于压缩感知理论的无源成像技术得到广泛研究。其中，文献[5]依据目标散射点自身稀疏的前提，提出了基于正交匹配追踪技术的成像算法，在非均匀和稀疏空间谱填充情形下获得较好的成像效果；文献[6]则提出了基于两维SL0稀疏成像算法，通过对DVB-T信号进行仿真实验，表明了相比经典匹配滤波方法成像性能的提升。

然而，文献[5-6]应用稀疏重构技术时均要求精确已知观测矩阵。在实际雷达系统具体实现时，雷达回波模型不可避免存在着相位误差[7-8]。该误差通常由系统误差导致，比如在无源成像系统中，可能是由收发阵元的位置误差所引起，这会使得回波模型中的观测矩阵部分未知[9]，导致回波测量值与观测矩阵之间失配，将大大减弱传统稀疏重构算法的性能。其中文献[9]仅分析了接收机存在误差下的无源成像模型，提出基于低秩矩阵恢复的稀疏成像方法，对系统收发构型要求较高。

综上，本文首先构建了同时存在收发站址误差下的无源成像模型，接着从确定稀疏反演角度出发，提出了基于优化迭代技术的自适应相位误差校正成像方法，即在重构目标图像的同时消除相位误差对成像的影响，可以较好地克服文献[5-6]成像方法的缺陷。文中所提自聚焦成像方法是在回波数据域进行处理的，仿真表明其具有较好的适应性和稳健性，能够有效地解决相位误差造成传统稀疏成像方法重构性能下降的问题。

1 信号模型

本文的无源雷达成像模型如图1所示。以目标中心作为坐标原点，设第i个外辐射源假定的空间坐标为(ri,θi)，与真实位置的误差为Δri，其中i=1,2,…,I；同理，第j个接收雷达假定的空间坐标为(rj,θj)，与真实位置的误差为Δrj，其中j=1,2,…,J；目标任一散射点位置用(r,θ)表示。

si(t)=ui(t)exp[j(2πfit+φi)]

(1)

式中，ui(t)为信号复包络，Bi为信号带宽，fi为信号载频，φi为初相。

无源雷达的接收机通常配置两个接收天线，分别用来接收直达波和目标回波。接收机j获取外辐射源i的直达波可以表示为

(2)

此时，接收机j收到外辐射源i对目标的回波信号为

exp{j[2πfi(t-τij)+φi]}dxdy

(3)

式中，σ(x,y)为目标后向散射系数，τij=(rik+rkj)/c为辐射源i发射的信号经散射点k反射后到达接收机j的总时延，rik为辐射源i到散射点k的距离，rkj为散射点k到接收机j的距离。

将式(2)对应的直达波与式(3)对应的目标回波分别去载频之后，再对基带信号进行同步和混频处理，可以得到

{ui(t-τij)exp(-j2πfiτij)}dxdy

(4)

式中，⊗表示复相关运算，对t进行Fourier变换，记Ui(f)=F{ui(t)}，Zij(f)=F{zij(t)}，式(4)转化为

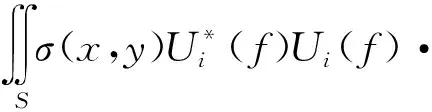
(5)

式中，f∈(-Bi/2,Bi/2)。实际成像场景通常满足远场近似条件：

rik≈ri-(r+Δri)·Ii

rkj≈rj-(r+Δrj)·Ij

(6)

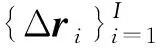
将式(6)代入式(5)，经整理后得到

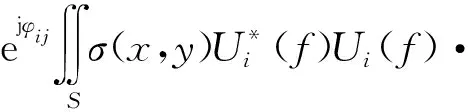
exp{j2π(fi+f)([x(cosθi+cosθj)+

y(sinθi+sinθj)]+Δri·Ii+

Δrj·Ij)/c}dxdy

(7)

然后设计滤波因子：

(8)

对式(7)进行频域滤波，得到相应的回波方程为

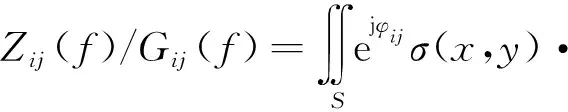
(9)

式中：

φij=φij-2π(f+fi)(Δri·Ii+Δrj·Ij)/c

(10)

定义分布式无源雷达的空间谱填充形式：

(11)

则发射机i和接收机j构成的接收通道对应的回波方程最终可写为

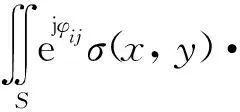
(12)

从式(12)可知，如果忽略相位误差因素的影响，目标散射系数与接收回波之间满足Fourier变换关系。

进一步，对成像场景S进行均匀网格划分，尺度为U×V，可将回波方程式(12)写成下述矩阵形式：

y=EAσ+n

(13)

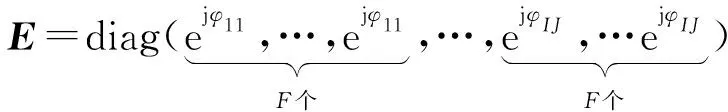
2 本文成像方法

首先，将式(13)转化为下述优化问题:

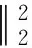
(14)

式中，ξ为与噪声功率有关的参数，g(σ)为表征目标稀疏先验的函数，常见的有l1[11]和lp范数[12]等。

然后，依据凸优化理论将式(14)转化为式(15)所示的无约束优化问题：

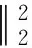
(15)

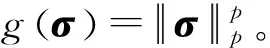
最后，采用交替迭代方式依次求解σ和E，具体步骤如下(设t为迭代次数)。

步骤1：目标图像稀疏重构——固定E(t)，求解σ(t+1)

此时，式(15)应转化为

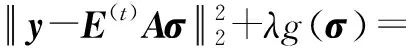
σHAH(E(t))HE(t)Aσ-yHE(t)Aσ-

(16)

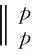
(17)

式中：

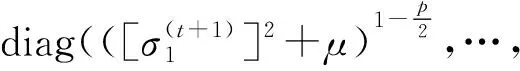
(18)

由式(17)可以得到σ(t+1)为

(19)

根据矩阵求逆的性质，式(19)可以转化为

(20)

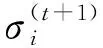
(21)

式中，Η=AH(E(t))HE(t)A+λpΨ-1/2。

σ(t+1,l+1)=σ(t+1,l)-ζ[H(σ(t+1,l))]-1J1(σ(t+1,l))

(22)

式中，l为新设置的内部循环次数，ζ为对应的迭代步长。

步骤2：相位误差校正——固定σ(t+1)，求解E(t+1)

此时，式(15)应转化为

minJ2(E(t+1))=

(σ(t+1))HAH(E(t+1))HE(t+1)Aσ(t+1)-

yHE(t+1)Aσ(t+1)-(σ(t+1))HAH(E(t+1))Hy+yHy

(23)

以无源雷达为例，假定φij相互独立，定义：

(24)

由式(13)得出回波方程满足yij=φijAσ(t+1)，将其代入式(23)，经整理得到

minJ2(E(t+1))=

(25)

式中，Const为常数项。

(26)

(27)

对式(27)展开处理，经整理得到

(28)

(29)

步骤3：参数更新

由于参数p的初值对成像结果通常有较大的影响，因此如果采用固定p的方式，则事先需要大量实验来确定合适的参数，这在实际应用中极不方便。据此，本文提出一种自适应调整参数p的方法，定义如下:

(30)

式中,NMSE为成像结果的归一化均方误差，ξ为较小的正数。仿真表明经过一定的迭代次数后p可以收敛至合适的取值。

3 仿真实验与分析

下面通过仿真验证所提方法的有效性。以无源雷达为例，7颗数字电视直播卫星的参数如表1所示，再设定4个接收机，均匀分布在(31°N～32°N)和(117°E～118°E)之间的地面上，回波通道的频率采样点数为5。

表1 7颗Ku波段数字电视直播卫星相关参数

原始成像目标是由5个幅值为1的散射点构成，如图2(a)所示。另外设置接收回波SNR=5 dB，相位误差浮动范围在(-π/4,π/4)之间。图2(b)～图2 (f)分别是MF、FOCUSS[15](基于lp范数约束的稀疏成像方法)、SBL[16](基于贝叶斯学习技术的稀疏成像方法)、文献[17](一种针对存在相位误差下的合成孔径雷达自聚焦成像方法)和本文方法的成像结果。可以看出基于Fourier重构技术的MF方法和传统基于压缩感知理论的成像方法受相位误差因素的影响比较大，因此成像效果较差。而文献[17]和本文方法均采用了自聚焦技术，均能准确地获得目标的空间位置，但是相比而言，本文方法在求解目标散射系数时具有更高的计算精度。

图3给出了SNR=15 dB时不同方法的成像结果对比，可以得到类似的结论。总体而言，本文方法相比其他方法具有更稳健的成像性能，即在求解目标空间位置及相应的散射系数时，具有更高的准确度。

4 结束语

本文针对无源雷达在实际应用时因存在收发站址误差导致传统基于压缩感知理论的成像方法性能恶化问题，提出了一种改进的稀疏自聚焦成像技术。首先推导了存在站址误差的成像模型，得出站址误差对成像的影响可以利用等效相位误差进行建模的结论。接着根据凸优化理论，从确定性反演角度出发，提出了基于优化迭代技术的自适应相位误差校正成像方法。最后利用仿真实验验证了所提方法的有效性，并展示了相应的成像性能提升。