城市轨道交通线网方案的群组决策优选模型研究

2018-07-17 06:20杨中杰张飞涟陈勇军Chencheng

铁道科学与工程学报 2018年7期

杨中杰，张飞涟，陈勇军，Chencheng

(1. 中南大学土木工程学院，湖南长沙 410075；2. 中南林业科技大学土木工程与力学学院，湖南长沙 410004；3. 旧金山州立大学工程学院，美国旧金山 CA94132)

城市轨道交通作为城市公共交通的重要载体，具有快捷、节能、运量大、安全和效益好等特点。截至2015年12月底，我国已有44个城市轨道交通规划方案获得批准，其中 26个城市城市轨道交通已正式运营，运营总里程共计3 618 km。城市轨道交通已成为我国新一轮城市基础设施建设的重要拉动力[1]。城市轨道交通的规划布置、线路走向对城市的发展布局、土地利用、城市化进程等有着重要影响，并且城市轨道交通项目投资巨大、工期长[2]，因此，城市轨道交通线网方案需要科学、合理规划。在城市轨道交通线网规划中，规划方案评选是关键环节，科学、系统的评价指标体系和评价方法是合理确定轨道线网方案的基础，从而确保最优或满意方案经济上合理、技术上先进、实施上可行[3]。国内外学者对于城市轨道交通线网方案评价方法的研究成果较多，评价方法主要涉及 DEA方法[4]、AHP 模型[5]、模糊综合评价模型[6−8]和灰色关联度方法[9]等，但这些方法在实际应用时均存在一定的优势与局限。DEA方法多通过数学规划的方法客观确定评价指标权重，但在面临多目标决策问题中容易出现几个决策单元同时有效以至于难以对多个方案进行严格的比选排序；AHP方法可通过利用较少的定量信息，将决策思维过程数学化，从而依靠主观评价对多个方案进行优劣排序，但过度依赖专家主观经验确定指标权重，容易因专家偏好而产生决策偏差；模糊综合评价法则是基于最大隶属度原则，根据模糊评价集上的值评定对象所属等级，一定程度上克服了传统数学方法评价结果单一的缺陷，但由评价指标相关性产生的重复评价问题难以解决；灰色关联度分析法可排除人为因素带来的影响，有效量化、统计评价指标，确保评价结果更加客观、准确，但由于其无法满足无量纲化处理的保序效应，容易扭曲各因素间的内在联系；TOPSIS方法可充分利用多个方案比选建立的决策矩阵中的信息，实现多个方案优劣的全排序[10]，但传统 TOPSIS方法通常认为评价指标属性权重一致，未能考虑评价指标权重不同的影响。另外，上述文献大多将城市轨道交通线网作为一个多属性单人决策问题，未能充分考虑到群组决策的问题，显然，由于各专家均在不同领域有所专长，其评判结果可能存在由于个人偏好所引起的偏差或某些专家过于提高或降低其对偏好或厌恶的评价，从而产生操纵评判结果的不良后果。因此，本文基于传统TOPSIS方法能够充分利用方案决策矩阵信息以及实现方案比选全排序的优点，综合考虑群组决策的群体性特征，基于专家群体理性行为确定专家权重以及评价指标属性权重，提出了基于群组改进的TOPSIS城市轨道交通线网方案决策方法。

1　城市轨道交通线网方案评价指标体系的构建

城市轨道交通线网评价指标体系是城市轨道交通线网评价的基础与前提，也是影响线网方案评价及决策结果的关键。李静等[11]以科学、有效评价城市轨道交通网络规划方案为目标，构建了包括线网结构特征、社会经济效益、建设实施性等5个一级指标以及平均站间距、工程难易程度、投资估算等 20个二级指标的城市轨道交通网络方案体系；张桐等[12]充分遵循科学性、可比性、合理性等原则，在综合考虑城市轨道交通网络特有功能要求的基础上，构建了包括线网结构特征、建设可实施性等5个一级指标以及线网站点总数、换乘次数等31个二级指标的城市轨道交通项目线网规划方案综合评价指标体系；沈犁等[13]基于合理性、客观性、层次性等原则，经过系统性的城市轨道交通线网评价指标分析评选，构建了包括服务水平、社会效益等5个一级指标及换乘节点数、平均出行节约时间等12个二级指标的城市轨道交通项目线网规划方案综合评价指标体系。另外，还有一些学者也对城市轨道交通线网规划评价指标体系的构建展开深入探讨[14−16]。上述文献中构建的城市轨道交通线网方案评价指标体系总体上基本反映了影响城市轨道交通线网规划方案的关键因素。在拟定城市轨道线网方案时，应着重强调线网结构特征与建设实施性，充分考量城市轨道交通线网运营效果与社会经济效益，体现城市轨道交通线网规划对城市格局和发展形态的引导作用，突出轨道交通运输与城市发展的协调性以及可持续发展。

本文经过分析相关资料和文献[4−16]的高频指标，结合城市自身规划和发展的要求及轨道交通线网的功能要求，并且根据国内近年线网规划评价的成功经验，本着科学性、层次性、可操作性、定性与定量相结合等原则，构建了与时俱进的城市轨道交通线网评价指标体系，如表1所示。

表1　城市轨道交通线网评价指标体系Table1　Evaluation index system of urban rail transit road network

2　基于群组 TOPSIS的城市轨道交通线网方案决策模型

现代社会经济决策问题客观上强调多参与者的作用，决策必须能够反映受其影响的利益主体的愿望和要求，且需要兼顾社会、经济、环境可持续发展，群体决策在现代组织中越来越普遍。城市轨道交通线网规划方案优选涉及多个评价指标的综合衡量，为实现方案优选的效益最大化，决策部门倾向采用科学的决策方法，集结大量专家的评价意见，因此，城市轨道交通线网方案优选是群组决策。在群组决策过程中，由于各专家均在不同领域有所专长，其评判结果可能存在由于个人偏好所引起的偏差或某些专家过于提高或降低其对偏好或厌恶的评价，从而可能产生操纵评判结果的不良后果，为降低决策者偏好对决策结果产生的不良影响，本文基于决策者群体理性行为确定决策者地位矩阵以及评价指标属性权重。

TOPSIS方法是Hwang等[17−18]于 1981 年首次提出的一种多属性决策方法，其核心思想在于根据多个方案与理想化目标的相对接近度进行排序，从而对方案的相对优劣进行评价。TOPSIS应用灵活、计算简单、结果量化客观，充分利用多个方案比选建立的决策矩阵中的信息，实现多个方案优劣的全排序。因此，本文基于专家群体理性行为确定专家权重以及评价指标属性权重的基础上，结合TOPSIS方法对城市轨道交通线网方案进行排序和优选。

2.1　城市轨道交通线网方案决策模型准备

对于某一城市轨道交通线网方案决策问题，设有 f位决策者(专家)(d =1,2,…,f)参与决策，可供选择的线网方案有n个,分别表示为(k =1,2,…,n)，对线网方案进行评价的属性集(评价指标)为，若某个ui又由j(j=1,2,…)个子指标属性组成，则记为Uij=，且令=x，即总共有x个子指标属性。

1) 决策者ed对于线网方案pk按属性uij进行评价，得到ed关于属性uij的属性值为，从而构成线网方案pk的决策矩阵。

2) 由于各评判指标的重要程度一般不同，因此，群体对每个指标 ui(i =1,2,…,m)赋予一个权重ωi，且ωi满足条件：=1；同理，群体对每个子指标uij(i =1,2,…,m)(j=1,2,…)赋予一个权重ωij，且ωij满足条件：=1，表示该属性在总体评判中的重要程度。

3) 决策群体一般由多个专家组成，专家们各自经验、擅长领域、个体偏好等因素的差异，对每个指标的认定存在着不同的看法，因此，针对每个指标给每个决策者 ed(d=1,2,…,f)赋予一个权重，表示在总体评判中在ujij的重要程度，且 u ∈U ，=1，因此，所有可组成一个决策者地位矩阵，该决策者地位矩阵基于群体理性行为求解。

2.2　基于群组 TOPSIS的城市轨道交通线网方案决策模型步骤

2.2.1决策矩阵的规范化

属性类型一般有效益型、成本型、偏离型、固定型等。为了消除不同物理量纲对决策结果的影响，决策时应对决策矩阵规范化处理。评价指标类型不同，规范化处理方法也不同，对于常用的效益型和成本型决策值可分按下式处理：

从而，线网方案 pk的决策矩阵 A(k)=((k ))可以规范化为R(k)= (。f×x

2.2.2基于群体理性行为的专家权重的确定

利用群组决策方法进行线网方案的选择，决策者判断信息的集结是其关键所在。如果决策者组中各成员的决策权重一样，则该决策者组是平权决策组。否则就是异权决策组[19]。显然，在实际群组决策过程中，由于决策者的专业背景、知识、能力等存在差异，其判断信息质量水平也不尽相同，即应为异权决策组。本文采用决策者群体理性行为解决专家赋权问题。

每个决策者 ed对包括自己在内的所有人在 uij的重要程度进行打分，按照由重要到不重要的顺序依次将重要性得分1,,1,…-ff赋予每位决策者，当几个决策者同样重要时得分相同。记由决策者 ed在属性uij上给定群体决策专家的重要性得分为，则决策者对群体决策专家的重要性评分矩阵记为：

式中： d =(1 , 2,…,f )。将f个Bd集合进行整理，得到全部决策者在属性 uij的总得分矩阵，归一化处理后得到全部决策者在属性uij上的专家权重：

从而构成决策者地位矩阵：

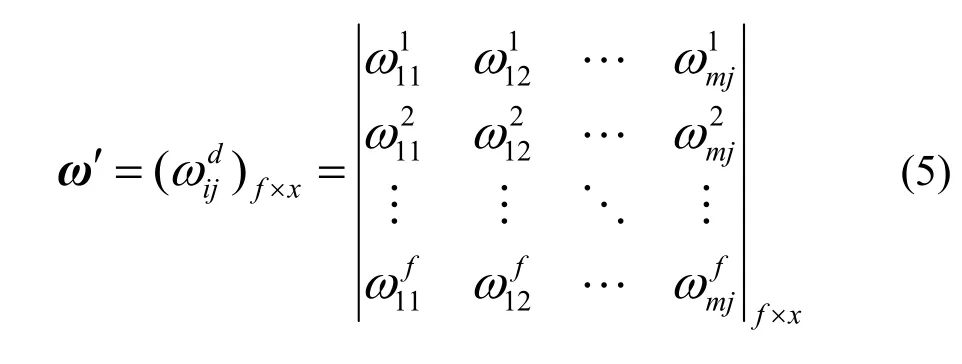
2.2.3属性权重的确定

对于评判属性uij，按照评判属性重要到不重要的顺序，决策者ed分别把重要性得分1,,1,…-xx赋予这些指标，当几个评判指标同样重要时得分相同。记由决策者ed给定uij的重要性得分为dijg ，得到群体决策者关于评判属性的得分矩阵为：

求得uij在群体决策评分的加权总得分为：

式中：)(ijuω表示评判指标uij在群体意义下的相对重要程度。将)(ijuω归一化处理得到集结决策者个体偏好的评判指标的权重ωij为：

同理，可以求得集结群体决策者个体偏好的评判指标 ui（i= 1 ,2,…,m）的权重 ωi。

2.2.4基于TOPSIS确定最佳城市轨道线网方案

集结线网方案 pk的决策矩阵以及决策者地位矩阵，群体决策者对于线网方案pk关于属性uij的综合属性值为：

则群体决策者对于线网方案 pk所有属性的综合属性值组成n维行向量：

从而，群体决策者对n个线网方案多属性决策的综合属性值组成 xn× 矩阵Z。

显然，集结群体决策者决策地位矩阵以及线网方案的决策矩阵的综合属性值矩阵Z是规范化数值矩阵，因此正负理想解值可以分别表示为：

结合属性权重，可以计算出各候选城市轨道交通线网方案与理想最优解及最劣解向量的距离为：

从而，可以得到各线网方案的贴近度为：

因此，根据贴近度的大小可以对各线网方案进行评价排序，贴近度大者为优，小者为劣。

3　实例分析

本文以文献[14]中长沙市的轨道网络规划方案为例，对基于群体理性行为的TOPSIS的城市轨道交通线网规划方案综合决策方法进行分析和验证。

长沙市轨道交通目前已正式开通运营贯穿中心城区的1号线和2号线，运载着城区南北和东西的客流量，形成了“十字形”主骨架的城市轨道交通线网。根据长沙市城市轨道交通线网总体规划和分阶段建设目标，经济实力以及客流需求，长沙市轨道线网交通建设规划在现有 1 号线和 2 号线的基础上，新增城市轨道建设6 条线路，共计134.1 km，据此提出了“中心放射”、“棋盘放射”和“环加放射”3个轨道线网交通线网规划备选方案[20]。

针对长沙市城市轨道交通线网规划的3个备选方案，组织4位专家进行群组决策。依据统计资料、现场测量数据、文献[14]的数据以及专家自己的经验、偏好等，4位群体决策专家针对15个二级评价属性指标uij采用5级评分标准分别对备选线网方案构造决策矩阵如下所示。