浅谈概率论在生活中的应用

◎孙宏国

(沈阳理工大学，辽宁　沈阳　110168)

概率是表达不确定性的一门艺术.概率一词最初是用来表示“值得肯定的”，在后来的使用中才渐渐有了“可能的”“合理的”这一层意思，这才跟随机性产生了联系.不管你是否愿意承认，概率的确主宰着我们的生活.如果你曾经过着赌徒式的生活，那你必然已经痛苦地意识到了这一点.概率的作用随处可见，如确定保险费用、新药物的引用、民意调查、天气预报和法庭上出示DNA的证据.不仅如此，概率还关系到我们每一个人.下面举几个应用概率的知识来解释生活问题的例子.

一、利用事件的独立性设计游戏规则，以保证公平性

二、全概率公式在预测公交车晚点问题上的应用

如果你是生活在拥堵城市的上班族，那么公交车是否能准点到达是你最关心的问题了.周日晚上你和你的同事小卓、小欧在酒吧小酌.你们讨论起了每天上班都要坐的那趟公交，大概只有60%会准点.下面你们就未来五天这趟车能准点到达的情况做一下预测.看看谁的准确率高.用L和T分别代表“晚点”和“准点”.小卓列出了两个L，三个T；而小欧写出了五个T，那么最有可能完全正确的会是谁呢？现在我们来算一下.如果你预测的是T，而公交又是准点的话你就对了，这一概率是0.6.而准确预测晚点的概率为0.4.因此，依据全概率公式.你一天预测准确的概率为0.6×0.6+0.4×0.4=0.52.如果你五天都预测正确的概率为0.525≈0.038；小欧能准确预测的概率为0.65≈0.078；小卓能准确预测的概率为0.63×0.42≈0.035.从这三个数值来看出，虽然每个数值都比较小，但显然相对来说，小欧更占有优势.

三、利用二项分布讨论弱旅赢得比赛的可能性

运动已然成为当下最流行的话题.有运动就会有竞赛.现在有两种赛制：① 一场比赛决胜负；② 七场比赛.哪一种赛制对于弱旅来说更有利呢？这里我们排除主场优势，以及其他一些复杂的原因，只可考虑每场比赛弱旅赢得比赛的事件是相互独立的，概率为p.在赛制②下赢得比赛，就要赢得四场比赛，那么弱旅会赢的概率为

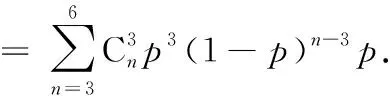
然后再代入不同的.例如，某球队每场比赛能赢的概率为0.2，那么它在赛制②下赢得比赛的概率只有3.3%.所以在赛制①下爆冷获胜的概率更高.

四、贝叶斯公式的广泛作用

贝叶斯公式是由著名的数学家托马斯·贝叶斯提出的.但是贝叶斯自己并没有公开发表这一重大发现，而是他的朋友在他去世之后整理他的遗稿时发现的.

让我们来举一个例子吧.我们知道，在自然人群中，有1%会得某种病.在自身没有不适的情况下，被诊断者去做某项试验，其准确率为95%.那么当试验反应是阳性时，被诊断者患有这种病的概率是多少？这个问题看起来很简单.如果检查的准确率为95%，那么你得病的概率就是95%.这样对吗？让我们用贝叶斯公式算算吧.令A表示事件“试验反应为阳性”，D表示“被诊断者患病”.已知P(D)=0.01，即发病的概率为0.01.而化验的准确性就是P(A|D)=0.95.现在要计算的是当化验的结果是阳性时，你患病的概率是多少，即求P(D|A)的值.由贝叶斯公式得，

所以其实被诊断者只有16%的可能可以确定是患病的！即使化验的结果准确率高达95%，你也可以保持谨慎的乐观，因为你真正患病的概率很低.计算有问题吗？当然不是.这里有两点：① 这个病非常罕见，所以你基本不可能患病；② 这个化验非常的精确，所以当检验结果是阳性时你很可能就患病了.这两个信息量化之后对应的概率分别是1%和95%，所以实际的风险在这两个数之间.而我们算出来的结果就是在这两个数之间.当你更深入地了解了概率，它们就成为你的朋友.它们值得你认真对待.因为，正是它们决定着我们每个人的一生.让我们在概率的世界徜徉肆意吧！