随机产出情况下权力结构对供应链的影响

冯　春，李灵燕，方晓舒

(西南交通大学 交通运输与物流学院，四川　成都　610031)

0　引言

现实生活中存在许多这样的例子，一个分销商向一个生产商订购一定数量的产品，但是由于生产商的生产系统具有随机性，常常出现供需不匹配，进而引起一系列供应链运作问题。许多行业的生产系统都具有随机性，如农业(生产蔬菜或鸡蛋)、化工业(生产专用化学物品或量身定做的化学品)及电子业(特殊处理器或硅片)。产出随机性可能会引起产品数量不定及不一致问题，进而降低产出数量，引发供不应求的局面，带来缺货损失；另外，产出过量可能增加生产成本、库存成本，甚至引起高破坏成本(如生产过量危险化学品)。

目前有关供应链的研究大都基于生产确定的情况，将产出随机性考虑到供应链的还比较少。1958年，Arrow等[1]首先提出随机产出和随机需求的研究，探究了批量产品数量服从固定分布情况下的单阶段库存问题；Khouja[2]总结了一些单阶段报童模型的文献，并将报童问题扩展到11类，其中包括产出不确定性，为后来的研究做出了重要的贡献；Keren[3]将随机产出下的单阶段库存问题扩展到供应链中，但是并未提出一个统一的产出不确定性模型，而是假设产出随机性服从均匀分布；Li等[4]针对Keren研究的不足，分析了一般分布下，随机产出对供应链成员绩效的影响及分销商的最优决策问题，但是并未讨论产出不确定性如何影响供应链成员最优决策。另外，He等[5]讨论了在生产商受产出不确定性和零售商受服务水平限制下，供应链成员决策顺序对供应链的影响；Inderfurth等[6]研究了随机产出和确定需求下的供应链风险分担契约协调问题。国内关于这方面的研究更少。赵霞等[7]研究了随机产出和需求服从均匀分布下的供应链收益共享合同；王道平等[8]将产出不确定性考虑到供应链中，并讨论了风险分担协调模型；彭红军等[9]研究了两级生产与随机需求下供应链的风险分担契约与模型。

综上所述，目前将产出随机性考虑到供应链的研究还不是很多。本文结合供应链结构多样化的特征，基于前人的研究，在随机生产和固定需求情况下，讨论了权力结构及随机产出对供应链的影响。基于此，为了更准确地解释权力结构对供应链的影响，本文将解决以下问题：①供应链主导方成员是否受益于其主导权;②权力结构如何影响供应链绩效;③不同权力结构下，产出随机性如何影响供应链成员决策、绩效及整条供应链的绩效。

1　模型解释及建立

本章主要解释权力结构在3种非合作博弈中的定义，并利用博弈理论建立不同主导方下的博弈模型，求出均衡解。

关于供应链权力的定义，目前还没有统一准确的描述，但在文献中关于其概念的理解大都一致(Cartwright[10],El-Ansary 等[11],Dahl[12],Emerson[13])，即供应链成员的权力是其控制处于供应链不同水平的其他成员改变决策的能力。权力结构与权力存在一一对应的关系，即不同成员的权力对应不同的权力结构。关于权力结构的表示方式，本文采用常用的时间序列法，通过不同的时间序列来表示供应链各成员的反应序列(Vol[14],Moorth等[15])。该规则通常认为首先进行决策的成员比供应链中其他成员拥有更大的权力。

本文将研究对象定为一个生产商和一个零售商组成的二级供应链。结合权力结构的表示方式，利用生产商或零售商决定计划生产量或订购量的不同时间序列来表示权力结构，即首先决定计划生产量(订购量)和生产商(零售商)在供应链博奕中占主导方。据此定义，可列出生产商主导(Manufacturer Stackelberg，MS)、Nash均衡(Nash Stackelberg，NS)和零售商占主导(Retailer Stackelberg，RS)3种非合作博弈形式。利用Stackelberg博弈建立生产商和零售商分别占主导时的供应链模型，利用Nash博弈建立生产商和零售商同时做出决策的均衡模型。

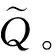
1.1　乘法随机产出模型

本文认为乘法随机产出模型中，生产量受随机产出的影响会发生剧烈波动，因此用乘以x的形式来表示，即实际产出数量为x·Q。不失一般性，本文假设0≤a≤x≤b≤+∞。

(1)生产商占主导模型(MS)

在这种情况下，作为供应链的主导者生产商首先决定计划生产量，零售商作为追随者，依据生产商的决策做出下一步反应。博弈顺序为：生产商首先根据外生批发价格w制定计划生产量Q，然后零售商依据生产商的决策决定订购量q。此时，生产商的总期望利润函数为

表1　模型符号

(1)

零售商的收益函数为

πr(q)=(p+hr+sr)min(xQ,q,D)-

(w+hr)min(xQ,q)-srD。

(2)

利用逆推法求解过程如下：

1)当q≥D时，求E[πr(q)]关于q的一阶和二阶导数得：

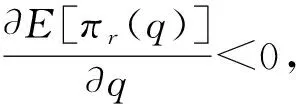
当q≤D时，求E[πr(q)]关于q的一阶和二阶导数得：

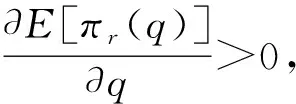
2)在条件1)下，生产商做出下一步反应，其目标收益满足

对式(1)求关于Q的一阶和二阶导数得：

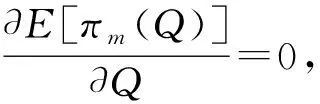
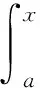
命题1生产商占主导下，存在最优计划生产量Q*和最优订购量q*，使得生产商和零售商的期望利润最大，且

(3)

命题1展示了供应链成员的最优决策，即最优计划生产量和最优订购量。其中最优计划生产量为需求量的线性函数，最优订购量等于需求量。说明生产商占主导的情况下，受生产随机性的影响，生产商调整了其计划生产量，零售商的订购量并未受影响。这暗示着生产商通过调整其生产数量来缓解生产随机性的影响，会引生产商与零售商之间产需不匹配的矛盾，即产出不确定性加剧了供应链的产需矛盾。扰动因子ks变化越大，对产需矛盾的影响越大。另外由命题1中ks的表达式可知，ks受生产成本、批发价格及惩罚成本影响。根据命题1可以得出，生产商和零售商的最大期望利润如表2所示。

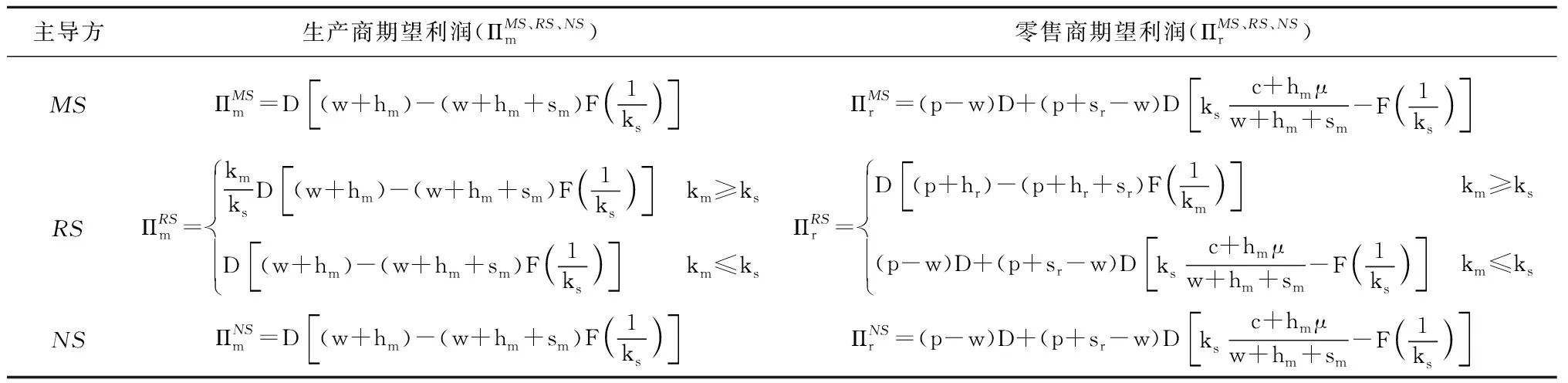
表2　乘法模型中生产商与零售商的最大期望利润

(2)零售商占主导模型(RS)

在这种情况下，零售商首先决定订购量，生产商根据零售商的决策决定最终计划生产量。因此模型的博弈顺序为：首先零售商根据市场需求量D向生产商订购数量为q的产品，然后生产商根据零售商的订购量制定计划生产量Q。利用逆推法求解：

1)求式(1)关于Q的一阶和二阶导数，可得：

。

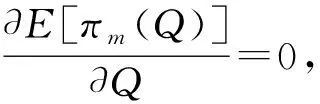
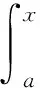
2)零售商以达到自身利润最大化为目标，做出下一步反应，其目标收益满足：

①当q≥D时，零售商的目标期望收益函数满足：

指导教师需要给出客观合理的评价，站在科研选题整体角度分析各小组的特色以及存在的问题，并针对问题给出合理的建议。从科研选题、科研方法、科研技术、科研内容及科研成果等方面对其进行全面系统的分析，促使学生不断提高科研能力。

maxE[πr(q)]=(p+hr+sr)E[min(xQ,D)]-

(w+hr)E[min(xQ,q)]-srD。

s.t.

将Q*(q)=ksq带入上式可得

对上式求q的一阶和二阶导数可得：

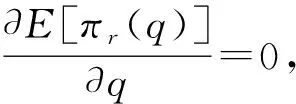
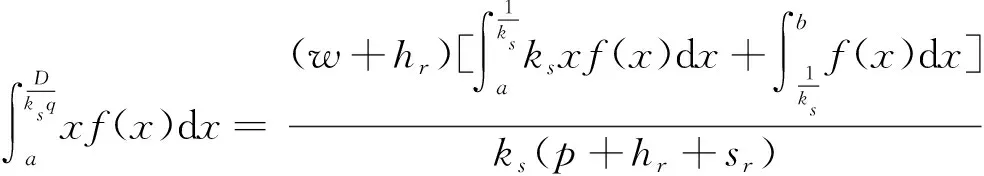
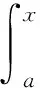
②当q≤D时，零售商的目标期望收益函数满足：

maxE[πr(q)]=(p+hr+sr)E[min(xQ,q)]-

s.t.

将Q*(q)=ksq，带入上式可得

E[πr(q)]=(p-w+sr)

对上式求q的一阶和二阶导数得：

因此零售商的期望收益E[πr(q)]是订购量q的单调函数，最优订购量q*=D或q*=0。因为q*=0意味着零售商未向生产商订购产品，交易未进行，所以将其舍去。

综上所述，可以得出命题2。

命题2零售商占主导下，存在最优计划生产量Q*和最优订购量q*，使得生产商和零售商的期望利润最大，且

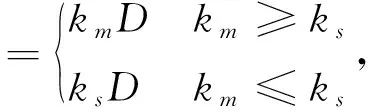
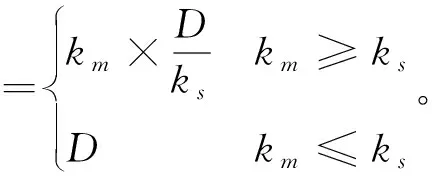
(4)

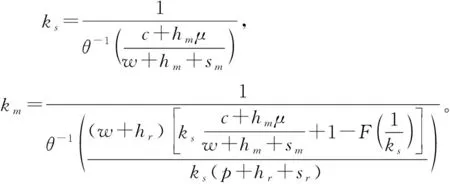
(3)Nash均衡模型(NS)

在Nash均衡博弈过程中，生产商和零售商都以自身期望收益最大化为目标，同时决定计划生产量及订购量，二者的决策不因对方的决策而改变。由此解得零售商的最优订购量等于需求量，生产商的最优决策与生产商占主导时的最优决策相同。因此Nash均衡博弈所得的最优解与生产商占主导一样，得命题3。

命题3生产商和零售商同时决策下，存在唯一的Nash均衡解使得供应链成员期望利润最大化。零售商的最优订购量为q*=D，生产商的最优计划生产量为Q*=ksD。

同时决策情况下，生产商的最优决策与零售商的最优决策相互独立，所求得的值与生产商占主导地位的情况一样，此时生产商与零售商的最大期望利润等于生产商占主导下二者的最优期望利润(如表2)。

1.2　加法随机产出模型

本文认为加法随机产出模型中，生产数量受影响因素的干扰引起局部变化，用加x的形式来表示，实际产出量为x+Q。不失一般性，假设a≤0,b≥0且-Q≤a≤x≤b，a为随机风险造成生产量损失的最低值，但是要保证生产量为正值，因此-Q≤a≤0，b为随机产出带来的生产增加量，b≥0。

(1)生产商占主导模型(MS)

生产商的总期望利润函数

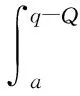
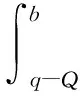
(5)

零售商的收益函数

πr(q)=(s+hr+sr)min(x+Q,q,D)-

(w+hr)min(x+Q,q)-srD。

(6)

利用逆推法和上文的求解思路求得命题4。

命题4生产商占主导下，存在最优计划生产量Q*和最优订购量q*使得生产商和零售商的期望利润最大，且

(7)

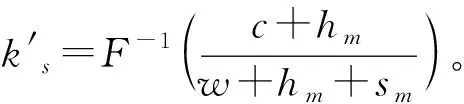
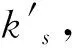
(2)零售商占主导模型(RS)

利用逆推法和Inderfurth 等[6]的求解思路求得生产商和零售商的最优决策，即命题5。

命题5零售商占主导下，存在最优计划生产量Q*和最优订购量q*，使得生产商和零售商的期望利润最大，且

(8)

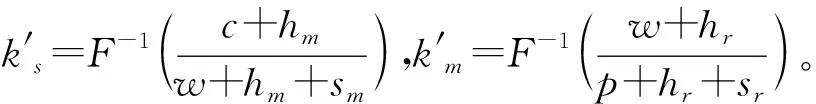
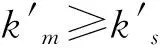
(3)Nash均衡模型(NS)

此种情况求得的最优解与生产商占主导一致，总结如命题6。

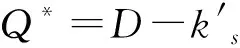
表3　加法模型中生产商与零售商的最大期望利润

2　影响分析

本章主要通过比较3种博弈均衡解，讨论权力结构和产出不确定性对供应链成员决策及收益的影响。

2.1　权力结构的影响

结合上文得到的最优解，比较不同主导方下生产商和零售商的最优决策与扰动因子，得命题7。

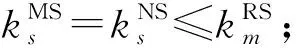
命题7的比较结果直观可见，随着主导权由生产商向零售商转移，生产商的最优计划生产量、零售商的最优订购量增大、乘法模型中扰动因子增大、加法模型中扰动因子减小。这是因为随着供应链中的零售商主导权增加，扰动因子增大(减少)，零售商的最优订购量由等于需求量到大于需求量，而生产商的最优决策与扰动因子呈线性关系，所以最优计划生产量呈线性递增(递减)。

比较不同权力结构下生产商与零售商的期望利润可得命题8(证明过程见附录1)。

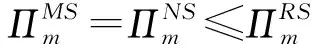
命题8说明，零售商占主导下，无论零售商还是生产商的利润均高于其他权力结构；另外，生产商占主导与双方同时决策两种情况下，生产商或零售商的利润都相等。从而揭示了受随机产出的影响，虽然生产商优先占有决策权，但是其获得的收益仍小于(或等于)其主导权减弱的情况。这暗示着生产商占主导地位时，其受产出随机性风险影响所带来的损失大于其作为主导者为自己挣得的收益；对于零售商占主导的情况，零售商加大订购批量减缓了其受随机产出的影响，同时其靠自己绝对的主导权又赢得了较高的收益，面对零售商大批量地订购产品，生产商为了避免缺货损失，必须增加生产量，因此零售商主导时双方的收益均增加。

为了分析权力结构对供应链绩效的影响，本文比较供应链整体期望利润得到命题9。

命题9乘法风险模型中，ΠMS=ΠNS≤ΠRS；加法风险模型中，ΠMS=ΠNS≤ΠRS。

由命题8不难得到命题9的结果，即零售商占主导下供应链的整体利润最大。说明零售商具有优先决策权时，为了缓解其受随机产出的影响，加大了供应链中产品的整体流量，使供应链整体效用增加。相比零售商作为追随者或主导权相等的情况，零售商拥有绝对主导权时，在提高供应链整体绩效的同时实现了Pareto改进。

由命题7～命题9可以发现，权力结构的变化在影响供应链成员决策和供应链绩效的同时，产出不确定性也在影响着供应链成员决策和供应链绩效。下面着重讨论随机产出对供应链的影响。

2.2　产出不确定性的影响

因为产出的随机性引起了供需不匹配的潜在成本，所以产出随机性影响供应链成员的最优决策。下面本文将讨论不同的权力结构下，生产随机性的变化如何影响供应链成员决策及其绩效。

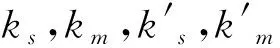
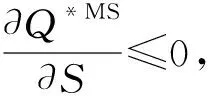
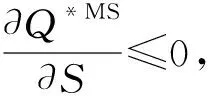
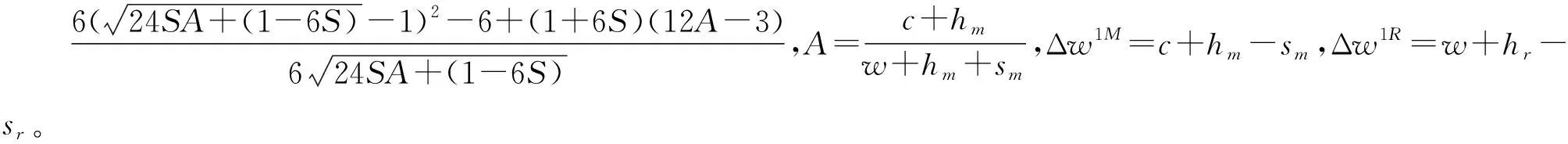
命题10说明，无论在加法还是乘法模型中，MS(或NS)下，生产商的最优生产量随产出随机性的变化与生产商的边际利润有关。当生产商的边际利润小于临界值时，最优计划生产量随产出随机性的增加而减少；当边际利润大于临界值时，最优计划生产量随产出随机性的增加而增加。零售商主导情况下，生产商的最优计划生产量随产出随机性的变化与零售商的边际利润有关。当零售商的边际利润小于临界值时，最优计划生产量随产出随机性的增加而减少；当边际利润大于临界值时，最优计划生产量随产出随机性的增加而增加。也就是说，生产商的边际利润大于一定值时，生产商会通过扩大计划生产量来缓解产出随机性，但是当生产商的边际利润小于一定值，生产商的生产积极性受到制约，不会提高其生产能力。

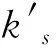
分析不同情况下，生产商和零售商的期望利润随产出随机性的变化情况如命题11所示(详细过程见附录3)。

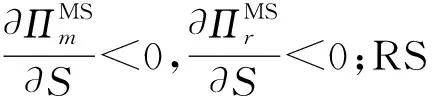
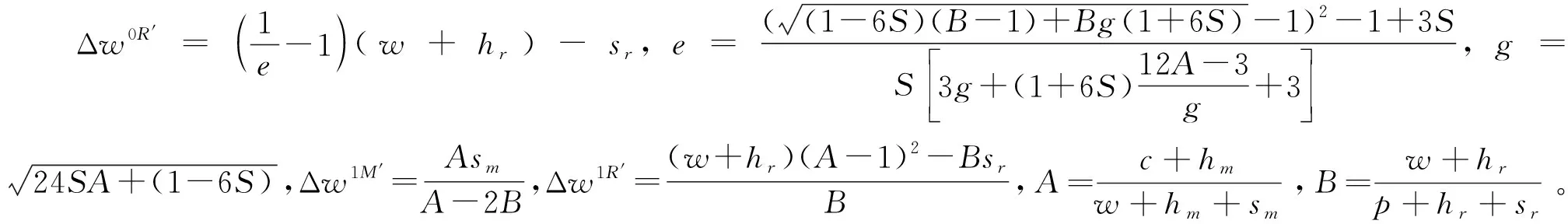
命题11说明，无论是加法还是乘法模型，MS(或NS)中生产商和零售商的利润随产出随机性递减。乘法模型中，零售商主导时，生产商的期望利润随产出随机性的变化无法确定，但是零售商期望利润的变化与其边际收益有关。当边际收益大于临界值时，其期望收益随产出随机性递增，这是由零售商增加订货量导致；当边际收益小于临界值时，其期望利润随产出随机性递减，这是由于面对较低的收益及确定的市场，零售商没有增加订购量。加法模型中，零售商主导时，生产商和零售商的期望利润随产出随机性变化与其自身的边际收益有关。当边际收益大于临界值时，生产商和零售商的期望收益随产出随机性递增；当边际收益小于临界值时，生产商和零售商的期望收益随产出随机性递减。

2.3　数值分析结果

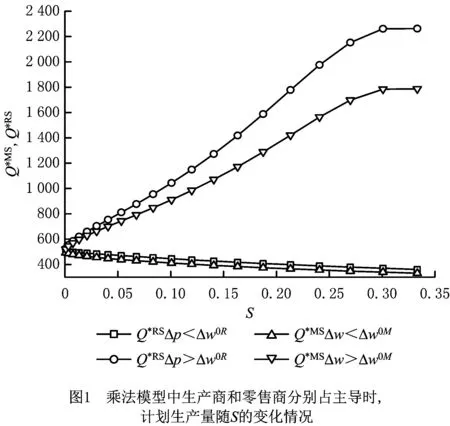
为了能够更清晰地看到3种非合作博弈中，供应链成员决策、期望利润及整条供应链的期望效益受产出随机性影响的情况，利用数值实验验证上文分析的结果。假设某生产基地向某超市供货，因为超市面临的市场(消费群体)比较固定，所以对某种产品的需求量固定，即D=500单位，每单位零售价格p=8，超市订购过量产品时的单位库存成本hr=1，订购小于需求时的单位缺货成本sr=0.5。生产基地投入生产的单位生产成本c=2，单位批发价格w=5，生产基地生产过量产品时单位库存成本hm=1，生产数量小于需求时单位缺货成本sm=0.25。以此系列数据为基准，改变参数值以满足条件要求，利用MATLAB 2016和Origin画出不同情况下，供应链成员决策、期望利润及整条供应链的期望效益受产出随机性影响的情况，如图1～图7所示。由上文讨论可知，Nash均衡情况下生产商和零售商的决策及收益情况与农户占主导时一样，因此只讨论MS和RS两种情况。

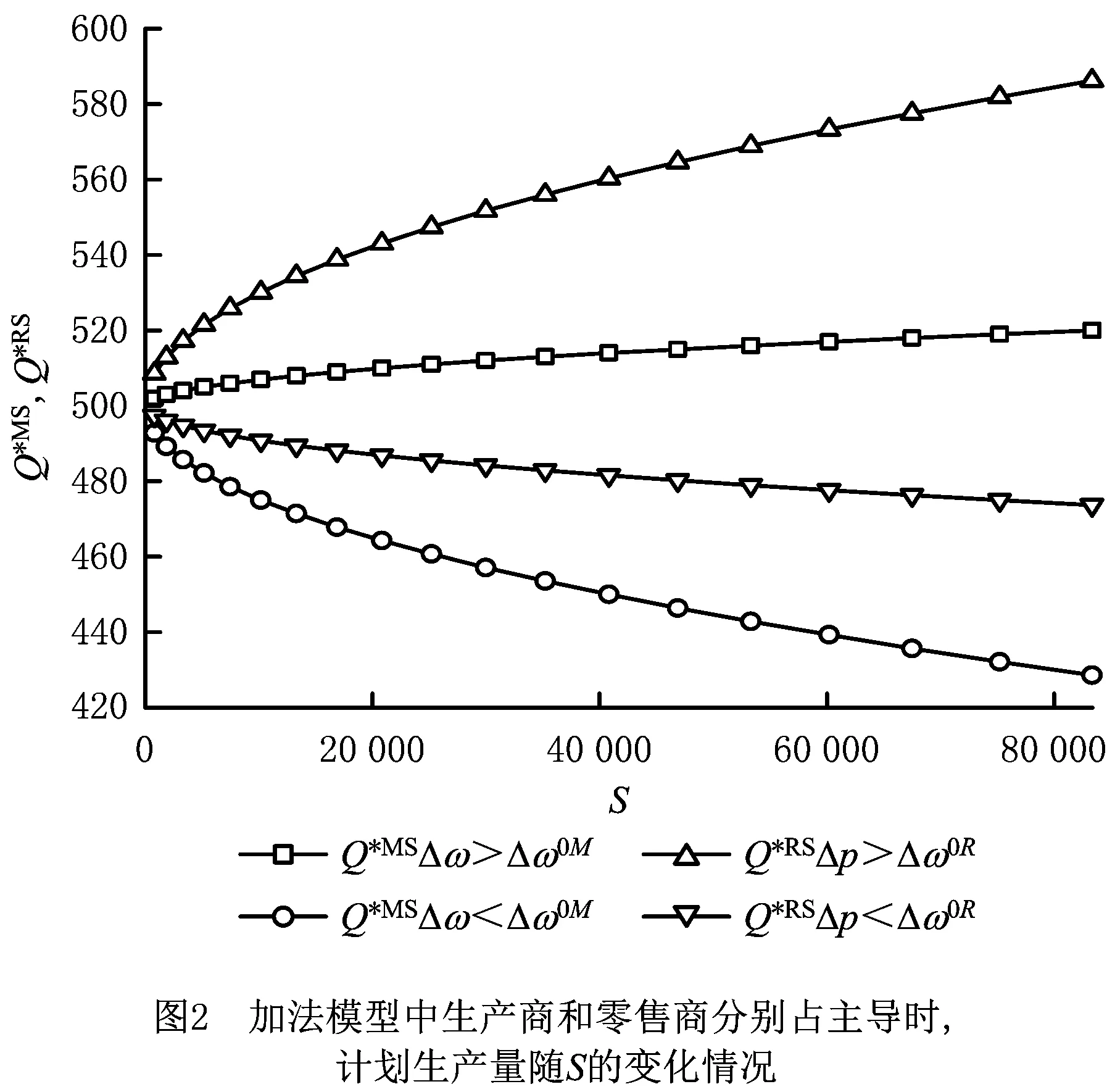
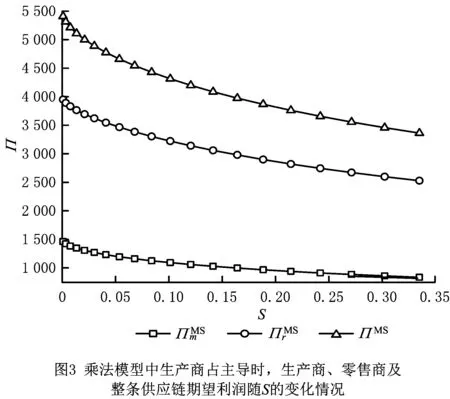
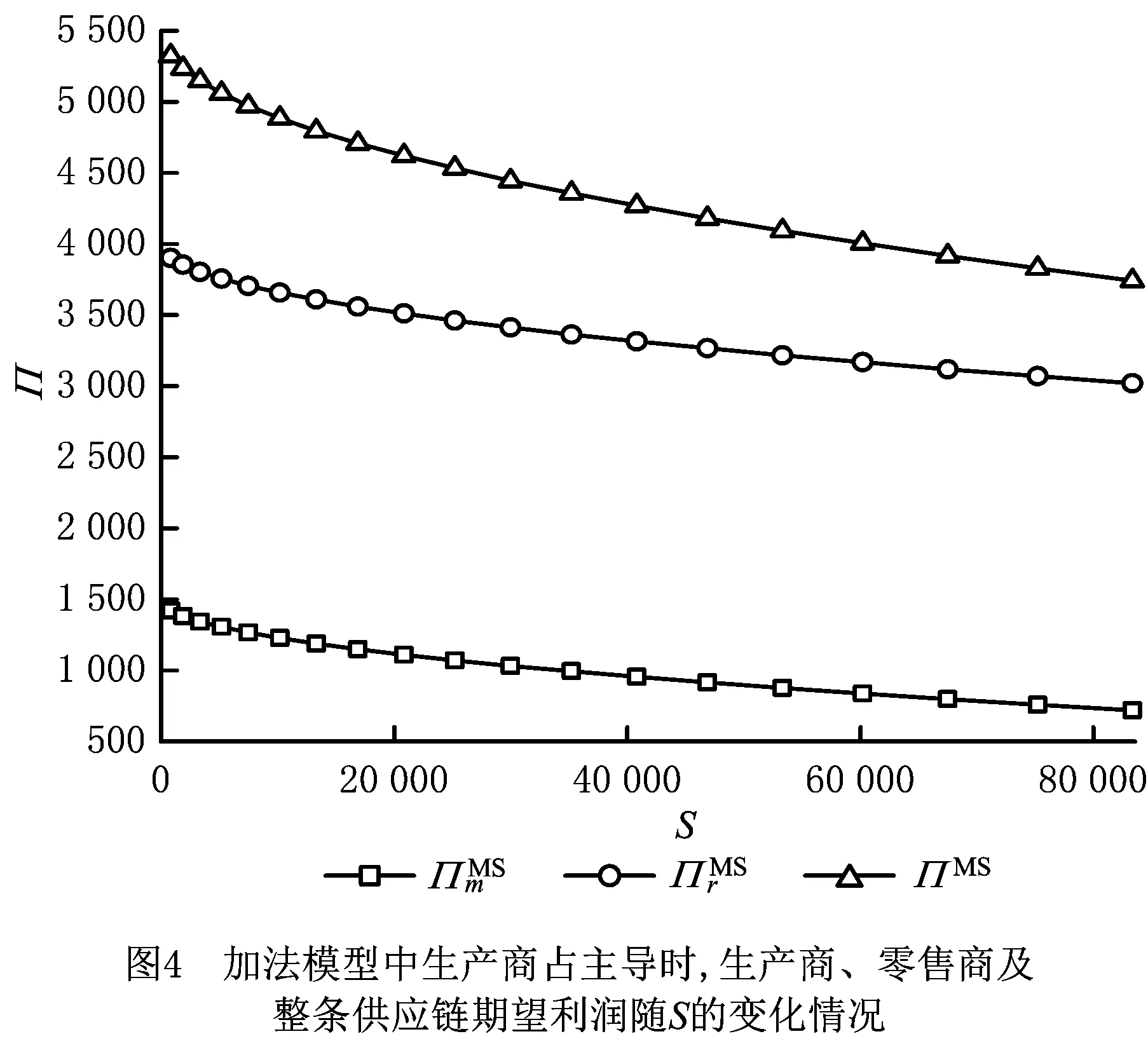
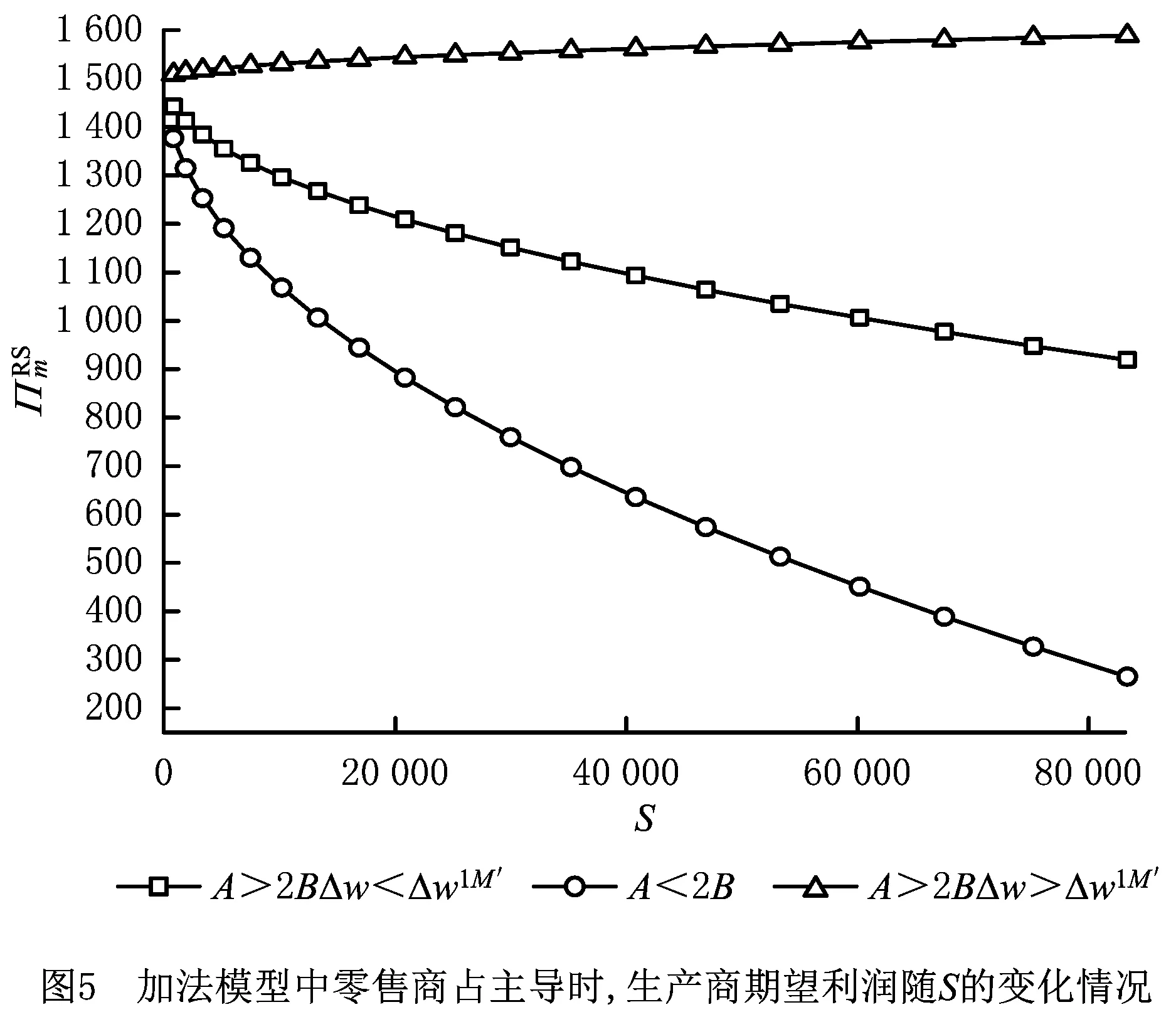
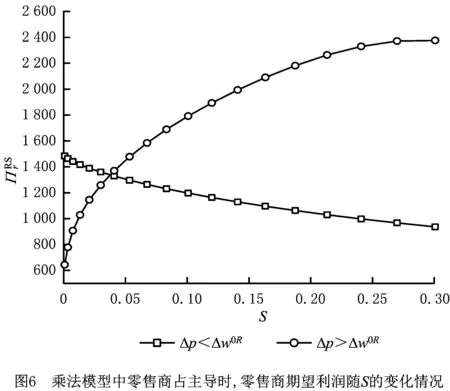
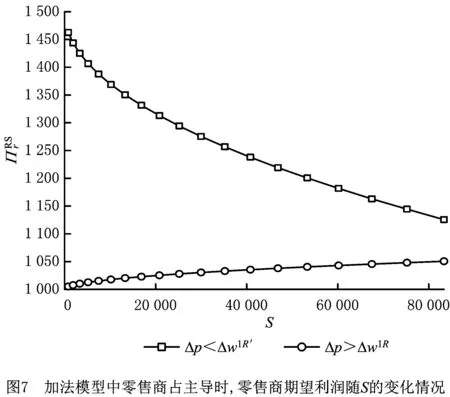
图1和图2分别表示乘法和加法模型中生产商的最优决策受产出随机性的影响。比较可知，无论加法还是乘法模型，生产商的最优决策受产出随机性的影响与其自身及零售商的边际利润有关。图1和图2与命题10的结论一致。在生产商占主导或同时决策时，生产商的边际利润大于临界值时，生产商利用加大计划生产量来缓解产出不确定性风险；边际利润小于临界值时，生产商面对双重风险，风险越大，生产意愿越低。然而，零售商占主导时，生产商受随机产出的影响与零售商的边际利润影响。这是由于零售商的边际利润大于临界值时，零售商会加大订购量，生产商随后加大生产量来满足零售商；当零售商的边际利润较低时，随着风险变大，为了避免更大的损失，零售商减少订购量，进而生产商也减少生产量。由命题1，3，4，6易知，不管乘法模型还是加法模型，生产商主导(或双方同时决策)时零售商的最优订购量基本不变。说明生产商主导(或双方同时决策)时，生产商是产出随机性的直接影响者和最大被影响者。由命题2和命题5可直接看出，零售商占主导时，为了缓解产出随机性，零售商扩大了订购量。说明零售商占主导时，生产商为产出随机性风险的直接影响者，但零售商为产出随机性风险的最大被影响者。

图3和图4表示，加法和乘法模型中，生产商主导(或双方同时决策)下，生产商的利润均随产出随机性风险的增大而减小。结合图1和图2发现，生产商主导(或双方同时决策)时，生产商不但为不确定性风险的直接影响者，而且为最大受害者，产出随机性风险增大所带来的潜在损失会不断削减生产商、零售商及整条供应链的收益。这是由于在这种情况下，生产商面临生产和需求信息双重不确定，生产商主观臆断判断生产量将导致供给量不稳定，给自身、零售商及整条供应链带来潜在损失。

零售商占主导时，虽然因乘法模型中生产商的利润公式比较复杂，无法利用数学方法求出其收益情况随产出随机性的变化，但是加法模型相对简单，可以求出其随产出随机性的变化趋势，如图5所示。图中显示，在一定条件下，当边际利润大于临界值时，生产商通过大批量销售产品获得的收益大于因产出随机性而损失的利润，与图6和图7的结果类似，即当零售商的边际利润大于临界值时，零售商的收益随产出随机性的增大而增大，这是扩大订购量的结果；当边际利润小于临界值时，零售商受产出随机性影响的损失大于扩大订购量获得的收益，故其利润下降。结合图1和图2发现，零售商占主导时，零售商的边际利润不仅影响自身的决策，还影响生产商的决策，同时决定着自身收益受随机产出的影响，即在一定条件下，生产商为随机产出的直接影响者，但是零售商却是供应链的最大受害者。因此零售商比生产商更渴望提升生产的可靠性，消除产出随机性。

3　结束语

本文建立了供应链的不同权力结构模型，分析了权力结构对供应链成员决策及供应链绩效的影响。在模型中，首先做出反应的供应链成员即为Stackelberg博弈的主导者，Nash均衡博弈中供应链成员同时进行决策。另外，产品生产者和销售者面临产出随机性风险，即产品产出系统具有随机性。研究发现，权力结构及随机产出对供应链成员决策及供应链绩效产生巨大影响，总结如下：

(1)供应链成员是否受益于其获得的主导权受随机产出风险影响。零售商主导时，生产商和零售商的收益均大于生产商具有主导权(或者双方同时决策)时的收益。

(2)权力结构对供应链效率的影响受产出随机性影响。相对于生产商占主导和双方同时决策的情况，零售商占主导时，供应链的总收益最高。

(3)生产商占主导或者双方同时决策时，生产商、零售商及整条供应链受益于随机产出风险的降低，生产商的决策受其边际利润和随机产出风险同时影响，零售商的决策不变。

(4)零售商占主导时，生产商和零售商的收益受益于其自身的边际利润的提高，生产商和零售商的决策受零售商的边际利润及产出随机风险的影响。

研究发现，供应链成员是否受益于其获得的优先决策权受随机产出影响。生产商作为风险的直接影响者，在获得优先决策权的同时也独自承担着风险，其应该与零售商签订契约，以在提前获得一部分需求信息的同时确保自身的边际收益。另外，降低产出随机性对生产商非常有益，生产商应该鼓励或者奖励零售商降低产出的不确定性。对于零售商来说，随着主导权的转移，其虽然不是随机风险的直接影响者，但是为最大受害者，因此应该确保自身的边际收益，当边际收益大于定值时，零售商得益于高产出不确定性风险。这意味着，当零售商试图降低随机产出时，必须在价格上考虑预期生产。

本文研究还存在一定的局限性。本文考虑的是一个生产商和一个零售商组成的单阶段二级供应链，虽然这是学术研究简单化的设置，但是生产商或零售商之间的水平竞争也会影响权力结构对供应链的影响；另外，本文假设随机产出服从均匀分布，虽然可以代表性的表示出产出随机性的影响，但是不具有统一性。这些局限性将作为未来的研究方向。