基于差分进化优化的BP神经网络图像复原方法
张 勇,何泽裕,赵东宁,张 席
1)深圳大学ATR国防科技重点实验室, 广东深圳518060;2)深圳大学信息工程学院, 广东深圳518060;3)深圳技术大学基础教学部, 广东深圳 518118
图像在获取过程中,因各种原因无法规避出现噪声干扰和失真等退化现象,而在光学、医学、天文学以及气象学等领域,通常对图像的清晰度和质量要求都比较高.同时,高质量的清晰图像也是计算机视觉和机器学习等技术应用的基础,故图像复原技术应运而生.图像复原通常都是采用最优化的准则来重建模糊图像,提高图像的质量,从而得到较为清晰的图像.因此,图像复原技术日益受到关注.
噪声模糊作为一种普遍存在的图片退化现象,其噪声可能来源于图像获取、传输、处理以及存储的任何环节中.例如,在利用照相机或摄像机采集图像时,传感器的温度和光照强度都是影响成像噪声数量的主要因素.而传输信道中存在的干扰也使图像在传输过程中容易被污染,如光照和电磁辐射等因素可能对通过无线传输的图像有所污染.而由于操作不当或者设备自身因素所带来的噪声也会使处理和存储的图像受到污染.根据图像退化理论,可以把符合一定条件的噪声近似当作高斯白噪声[1].
应用原始图像和噪声统计特征进行降噪复原是比较常用的传统图像复原方法,该方法需要已知点扩散函数,所以被称为非盲复原法,比较常见的有维纳滤波法、直接逆滤波法和稀疏表示法等.若模糊图像的点扩展函数未知,则只能采用盲复原法,其基本原理是由模糊图像的相关信息估计出模糊核函数,并结合先验信息和前提条件对问题进行约束求解[2],目前,盲复原方法在国内外都已经展开了大量的研究工作[3-6].但盲复原算法收敛速度慢,计算量大,而且复原结果稳定性一般.
Back-propagating (BP)神经网络是一种常见的盲复原方法,它具有十分强大的自我学习能力,可以实现一些比较复杂的非线性变换.与其他盲复原算法一样,若将BP神经网络直接用于图像复原,就会出现收敛慢、仅求得局部最小值等缺陷[7].如果BP网络一旦陷入局部最小值点,复原图像的质量就比较差,将达不到图像复原的要求.因此,需要对BP神经网络进行改进以用于图像复原.
本研究针对BP神经网络自身缺陷,提出改进差分进化算法(differential evolution algorithm,DE)来优化BP网络,并将其用于图像复原.该方法首先使用差分进化优化算法进行全局寻优,并将寻优结果初始化BP网络,然后使用样本图像训练BP网络,计算其输出,并评估网络性能.若网络性能达不到要求,则根据网络输出对BP网络权值进行调整,再进行网络训练,直至达到要求.最后,使用训练好的BP网络复原目标模糊图像.
1 BP神经网络
BP神经网络是一种采用逆向传播误差的多层前馈网络,有很强的鲁棒性和很高的容错性.多层前馈网络运用广泛,图1介绍了常见的3层前馈网络结构,即单隐含层(b1,b2,…,bm)、 输入层(r1,r2,…,bk)和输出层(w1,…,wn)3层BP神经网络.由图1可见,在BP网络中,神经元是由权系数关联在一起的,网络信息分布存储在神经元的权值系数中,神经元之间的映射关系包括线性与非线性,不同的函数映射关系可根据赋予网络不同的传递函数来实现.当网络输出(y1,y2,…,yn)与期望输出(t1,t2,…,tn)存在误差E时,网络将误差信号E反向传播,修正各层的权值以减小误差.鉴于此,运用模糊图像或者带噪声图像作为样本来训练网络,在未知点扩展函数的条件下,BP网络的自我学习能力能够实现模糊图像与原始图像之间的非线性映射,并进行拟合,从而实现对模糊图像的复原.

图1 3层BP神经网络Fig.1 Three-layer BP neural network
2 差分进化算法
2.1 算法描述
差分进化算法[9]是基于种群进化并且能够自组织优化的方法,具有种群个体协同搜索、共享种群内信息和记忆个体最优解等特点.DE具备以种群为基础的全局寻优能力,还具有简单有效的种群进化方式,这主要得益于DE采取差分策略进行个体变异.同时,DE具有较好的鲁棒性与较强的收敛能力,且不要求已知所求问题的特征信息,因此该算法非常适合用于求解复杂环境中的优化问题.
DE算法种群进化的完整过程包括“变异”、“交叉”和“选择”3个步骤.为了下一代保持竞争者的数目一致,种群中所有成员向量都必须作为预定目标向量进行一次“交叉”和“选择”操作.在种群进化的整个过程中,DE算法都会挑选当代最佳种群向量,并记录最优化进程.对新种群向量的形成,DE算法采用的是一种随机偏差扰动方法,这种方法能得到一个全局收敛性很好的结果.
为提高DE算法的收敛速度,本研究对经典的DE算法进行一些改进,形成改进的DE算法.
2.2 改进的DE算法
设待求解的优化问题为
(1)
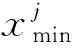
2.2.1 初始化种群

(2)

2.2.2 变异操作

1)DE/rand/1
(3)
2)DE/best/1
(4)
3)DE/rand-to-best/1
Vi,G=Xi,G+F(Xbest,G-Xi,G)+
(5)
4)DE/ best /2
(6)
5)DE/rand/2
(7)
求解最优解时,通常选择差分策略2),该策略能兼顾算法的精度和速度[10].由于种群向量的随机扰动是独立进行的,并以行方式搜索,为了实现变异的多样性,本研究改进了经典DE算法的差分策略2).在保存原来缩放因子的基础上,增加随机的微调参数,实现缩放因子的多样性,变异过程即可随之多样化.将改进的DE算法命名为随机缩放差分进化算法(random scaling-differential evolution algorithm, RSDE).此改进的目的是加快收敛速度,更快找到最优解.改进后的差分策略为
Vi,G=Xbest,G+[λrand(-1,1)+F]·
(8)

在种群进化过程中,为了确保解的有效性,需要保证染色体中各个基因都符合边界条件,即{Vi,GXmin≤Vi,G≤Xmax,i=1,2,…,NP}. 若某个基因不符合边界条件,则用随机方式生成新的基因替代,生成方式如式(2).
2.2.3 交叉操作
交叉也称为重组,也就是把几个父代个体根据指定的规则来实现交叉重组.DE最常用的交叉方式是二项式交叉,也就是将第G代种群Xi,G和变异的中间体Vi,G按照一定的规则进行混合来实现个体间的交叉操作,生成试验染色体
(9)
(i=1,2,…,M;j=1,2,…D)
其中,C为交叉概率;jrand为[1,D]的随机整数.如图2,对具有6个基因位的染色体进行交叉操作.为了较好地保持种群的多样性,需要保证任意的变异中间体Vi,G的染色体至少有一个基因遗传到下一代,第1个进行交叉操作的基因是随机取出Vi,G中的第jrand位等位基因,作为交叉后的试验染色体Ui,G第jrand位等位基因.后续的交叉操作过程,则根据随机数与交叉概率C大小的对比情况来选取Xi,G或Vi,G的等位基因作为Ui,G的等位基因.

图2 交叉操作过程Fig.2 Cross operation
2.2.4 选择操作
DE算法采用贪婪准则将试验染色体Ui,G与种群中当前预定的目标成员Xi,G进行比较,来决定试验染色体Ui,G能否成为下一代种群中的成员.如果是求解优化问题,那么对目标函数优化效果更好的染色体将成为下一代种群的成员.经过选择操作后,下一代的全部成员都应该比当代对应的成员对目标函数优化效果更优或者至少一样优.需要指出的是,在DE选择程序中试验染色体只与一个相对应的成员相比较,而不是与现有种群中的所有成员相比较.下一代种群中的成员Xi,G+1选择如下,
(10)
2.2.5 边界条件的处理
在有边界约束的问题中,必须保证各个参数向量位于规定的定义空间中,一个简单的处理方式是使用在定义空间内随机生成的参数向量替代不满足边界约束条件的成员向量.即
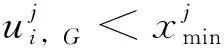
(11)
另一方法是根据式(11)重新生成试验染色体,然后采用二项式进行交叉操作,直到新生成的个体符合设定的约束要求为止.
2.3 RSDE算法流程
RSDE算法流程与经典的DE算法流程一样,本研究将RSDE算法进行了归纳(算法描述请扫描论文末页右下角二维码查看).
3 RSDE-BP图像复原方法
由于DE算法的种群相互独立、并行求优、收敛快和全局搜索能力强等优点,使该算法得到广泛应用.比如,CAMILO等[11]将多目标DE算法用于水下图像复原,提出将多目标DE算法用于水下成像造成图像模糊的复原.研究表明,该算法对水下成像模糊复原有较好效果,但文中只探讨了局限于水下成像特殊环境造成的模糊,对一般模糊的图像复原并未展开研究.目前国内外有关DE算法与BP网络结合的研究,取得了不少成果.文献[12]用DE算法在线训练BP网络,并用于医学图像识别,达到了预期的实验效果.文献[13]应用DE算法训练BP网络来预测地下水的水位.文献[14]应用混沌DE-BP算法实现电阻率层析成像的非线性反演.本研究提出了利用RSDE算法训练和优化的神经网络进行模糊图像复原.
3.1 神经网络参数的确定
网络层次、隐含层节点数和初始权系数等参数都是影响BP网络性能的重要因素.一般BP网络选择3层前馈网络就能够逼近任意多元的非线性函数,实现网络的非线性映射.
创建神经网络模型时,选取合适的隐含层节点数也极其关键,这不仅会影响网络性能,同时也有可能直接造成训练过程出现“过拟合”的情况.理论上,现在尚未有一种科学的选择方法来选取隐含层节点数.一般的原则是在保证网络高性能、泛化能力和满足精度的前提下,选取尽量少的节点数,通常采用以下经验公式估计隐含层节点数[15]
(12)
其中,NH表示隐含层节点数;Ni和N0分别表示输入层节点数和输出层节点数;k为1~10的常数.
另外,对初始值敏感严重影响着BP网络的收敛速度.当初始权值选取合适时,BP网络收敛得很快;当初始权值选取不合理时,收敛速度会变得很慢,甚至在训练开始阶段有可能会出现震荡,从而导致神经网络进入死循环,无法收敛.
RSDE算法不需要借助问题的特征信息,就能在复杂、多峰值的及不可微的大矢量搜索空间中快速有效地寻得全局最优解[13].将RSDE算法与BP网络进行结合,不仅能够解决传统BP网络存在的全局搜索能力不足的问题,同时也能够解决传统BP网络对初始值敏感的缺点,加快收敛速度,增强全局搜索能力.具体做法是应用RSDE算法求解BP神经网络的初始权值,解出近似的全局最优解,接着将求出的解初始化BP神经网络,再使用训练样本来训练神经网络,直到求得的解符合精度要求.训练结束后,使用训练好的网络复原目标模糊图像,最终实现对目标图像的复原.
3.2 RSDE-BP算法流程
本研究根据图像复原的特点,结合RSDE算法和BP网络的特点,设计出RSDE-BP算法的步骤(RSDE-BP算法的步骤请扫描论文末页右下角二维码查看).
3.3 图像数据预处理
本研究对图像的处理先要对图像的像素点进行归一化处理,再采用滑动窗口对模糊图像进行采样.
退化过程中,图像中像素点与旁边像素点联系紧密,距离越小,这种联系就越紧密.灰度值相同的点,若它的邻域不同,退化后其灰度值差别会很大.为充分利用邻域的像素点,图像特征采用滑动窗口结构来提取,获取 BP神经网络的输入.对于高斯模糊而言,3×3的滑动窗口足以利用领域的这种联系.图3(a)表示3×3的滑动窗口和采样,Pk为退化图像中某个像素点的8邻域,滑动窗口首先沿图像矩阵前3行从左到右滑动,然后是接下来3行,从而得到输入矩阵.图3(b)表示根据滑动窗口对原始图像采样,模糊图像的像素点Pk5对应于原始图像的像素点Tk5.

图3 输入采样示意图Fig.3 One input sample
当窗口滑过整幅模糊图像,即完成图像特征的提取,获得输入矩阵P. 提取原始图像对应像素点构成矩阵T. 矩阵P和矩阵T构成训练样本集(Pk,Tk)向量对.
3.4 参数设置及学习训练
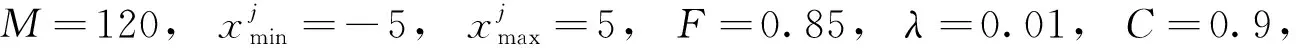
图像被分为训练集和测试集两部分,为方便起见,进行网络训练和测试的图像都选用大小为130×130像素、灰度值为256的图像.选取一些具有丰富的纹理信息的图像作为BP网络的训练集,以Lenna图像为例,训练图像如图4.

图4 训练图像Fig.4 Training images
用3.3节中所述的滑动窗口法获得网络的输入矩阵P, 原始图像的像素点作为理想输出矩阵T, 由于本研究选取的图像大小为130×130像素,因此,矩阵P和T的维数分别是9×16 384以及1×16 384.将训练样本(P,T)输入3.2节中设计好的BP网络进行训练,训练达到要求后,保存网络参数,如网络层的权值矩阵以及阈值矩阵等.选取BP神经网络、PSO-BP[7]以及DE-BP作为对比实验,以网络训练迭代次数和算法运行时间为指标来验证RSDE-BP的收敛速度是否提高.经过100次实验,对所有实验结果取算术平均后得结果如表1.平均迭代次数四舍五入取整数.
由表1可知,本算法在迭代次数和运行时间两方面都有所改善,收敛速度有所提升.改进的RSDE-BP达到了加快收敛的目的.训练结束后,对训练集的模糊图像完成复原,复原图像如图4(c).

表1 四种复原算法的收敛速度
3.5 图像复原
选取图像处理标准图形库中的Cameraman(Cam)、 Baboon(Bab)、 Barbara(Bar)、 Boats(Boa)、 Couple(Cou)、 Goldhill(Gol)以及Pepper(Pep)等图像进行模糊处理后作为模糊图像测试集,首先将图像数据预处理为形如P的标准输入矩阵,将其输入到训练好的网络中,计算网络的输出,可得到输出矩阵O, 将矩阵O逆变换为图像矩阵的形式,再反归一化即可得到复原图像.图5展示了7张测试图像采用不同复原算法所得的复原图像.
将图5第3列、第4列、第5列图像分别与第7列图像进行比较,可以发现,相比文献[7]的PSO-BP图像复原方法、文献[16]的ATV图像复原方法和文献[17]的TGV[18]图像复原方法,本算法对模糊图像的复原效果更好,在视觉上基本接近原图像,而且边缘保持和纹理细节处理也较好.对比图5第6列和第7列图像发现,DE-BP算法的复原图像与本算法的复原图像在视觉上差异很小,但在收敛速度方面,在前文对比中,可知本算法占优.在图5各行图像的对比中,可看出本算法的复原图像在视觉上优于对比算法.无论采用哪种图像作为训练集,本算法对人物图像、动物图像、景物图像以及蔬菜图像等类型的测试图像都能完成复原,复原效果良好,表现出不错的适应性.说明RSDE-BP算法在图像复原应用上,潜力巨大.
表2使用峰值信噪比(peak signal to noise ratio, PSNR)和结构相似性 (structural similarity, SSIM)评估各算法恢复图像的质量.其中实验结果均为100次实验所得算术平均值.通常PSNR和SSIM数值越大,反映图像恢复效果越优.峰值信噪比及结构相似性的定义如式(13)和式(14).
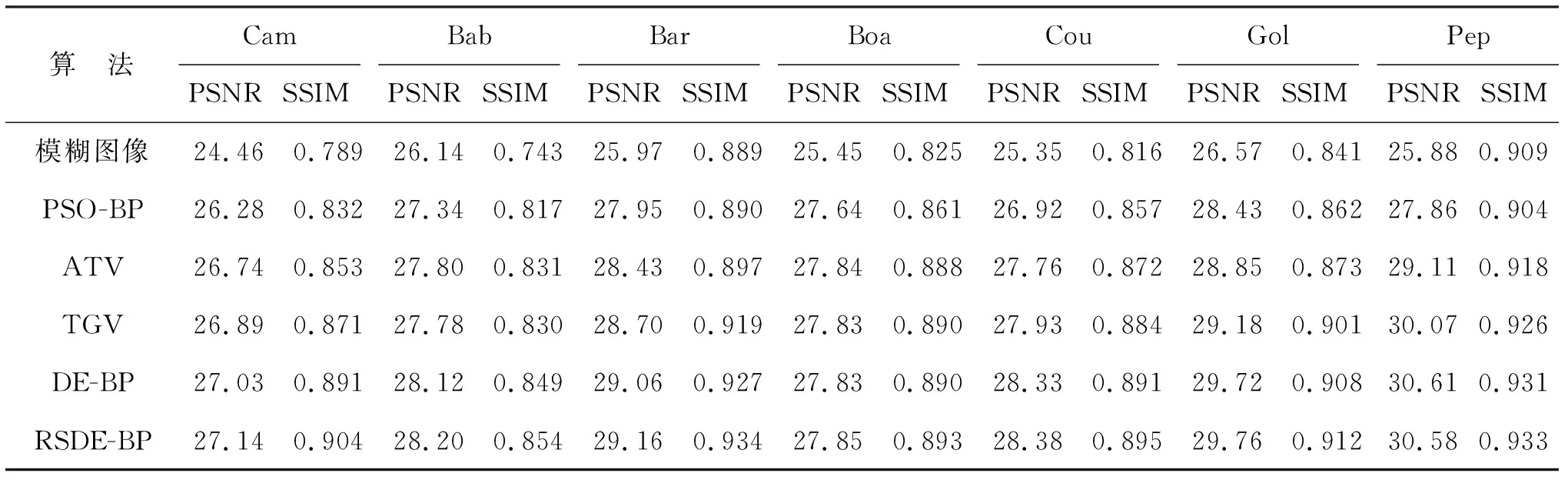
表2 五种算法复原图像的PSNR和SSIM
(13)

(14)
由图5可知,RSDE-BP算法复原的图像对应的PSNR值以及SSIM值总体上都相对较大,去噪性能优秀,结构性相似性更接近基准图像.相比PSO-BP图像复原方法[7]、ATV图像复原方法[16]以及TGV算法[17],DE-BP算法复原的整体效果更优.相比DE-BP算法,RSDE-BP算法复原效果也有所增强.由此可见,RSDE-BP算法是一种性能良好的图像复原方法,不仅可以有效地降噪去噪,而且在处理纹理细节和保持边缘信息两方面也同样表现出色.

图5 五种算法的复原图像Fig.5 The restored images of five algorithms
结 语
针对图像复原过程中,传统的BP神经网络本身固有的收敛速度慢、易陷入局部最小值点等缺陷,本研究利用差分进化算法改善BP神经网络的全局寻优能力,加快算法的收敛速度,并复原效果与其他4种算法进行比较.结果表明,本研究提出的RSDE-BP算法实现简单、参数较少,迭代次数少,收敛快.相比PSO-BP、ATV、TGV和DE-BP四种算法,本算法得到的复原图像无论在视觉效果上,还是峰值信噪比和结构相似性等图像质量评价指标上都有所增强.RSDE-BP算法用于图像复原,可有效降噪去噪,较好地复原图像.

