基于自适应高斯云变换的模糊控制器隶属度函数选取

王勇, 李聪, 黄汉桥,2, 周欢

(1.空军工程大学 航空航天工程学院, 陕西 西安　710038; 2.西北工业大学, 陕西 西安　710072)

无论是建模不够精确的传统控制还是规则来源于专家经验的模糊控制都是对现实世界的近似逼近[1]，而模糊控制在解决复杂非线性系统、难以建立数学模型的系统以及不确定内部扰动的多输入多输出系统的控制问题上可取得相比经典控制理论和现代控制理论难以达到的效果，已经成为实现智能控制中最重要、最有效和应用最广泛的一种形式。

为了推动模糊控制在工程界中的实际应用，研究者针对模糊控制器设计过程中的各个因素进行了广泛而深入的研究。文献[2-4]讨论研究了比例因子和量化因子对模糊控制器控制性能的影响，并提出了一定的选取准则；文献[5-8]则利用遗传算法或粒子群算法等智能算法在适应度函数的引导下对模糊控制规则进行了优化，以减少控制规则数目，降低模糊控制器的设计难度。但现阶段关于隶属度函数的研究成果却极其有限。模糊控制的输入输出论域是由它的隶属度函数来表征的，模糊规则之间的运算也是通过其隶属度函数的相应运算来实现的，隶属度函数的重要性可见一斑。文献[9]提出了模糊统计方法，即通过模糊统计实验来选定相应模糊集合的隶属度函数；文献[10]通过关专家评分直接给出隶属度函数；文献[11]采用了二元对比排序法，即将论域中所有变量属于某一模糊集合的优先程度进行两两比较，构建优先程度矩阵，然后基于矩阵通过取小法或加权平均法求得各变量的隶属度；文献[12]中提出的利用偏小型、对称型和偏大型3类模糊分布确定隶属度函数的作法则为现阶段广为接受的方法。此外，隶属度函数的确定方法还有范例法(Zadeh,1972)、范形变形法(Bremermann,1976)、隐分析法(Kochen和Badre,1976)、滤波函数法(Mac Vicar-Whelan,1978)以及模糊测度法(管道野夫,1998)等，但上述方法多是因研究对象不同而最终采取的方法不同，尚未出现一个统一的方法，如何精确确定一个模糊控制器的隶属度函数已经成为模糊控制应用的瓶颈。针对上述问题，本文在云模型理论的基础上，结合高斯云和概念含混度，提出了自适应高斯云变换算法对工程实践中的样本数据进行概念层次划分，利用最终所得高斯云的分布情况进而推断出模糊控制器中隶属度函数的数目、形状以及覆盖范围。最后，基于simulink仿真平台搭建的俯仰角模糊控制器设计了对比性数值仿真实验，验证了基于自适应高斯云变换算法所确定的具有特定数目、形状和覆盖范围的隶属度函数嵌套于模糊控制器之后可实现预期的控制性能。

1　隶属度函数提取

隶属度函数对模糊控制器控制性能的影响主要体现在3个方面：①隶属度函数的数目;②隶属度函数的形状;③隶属度函数的覆盖范围。现阶段关于模糊控制器的设计多是在未考虑实际数据分布的情况下依据专家经验人为预先给定隶属度函数的数目、形状以及覆盖范围，主观性强，难以量化。为了解决此问题，本文则利用自适应高斯云变换算法对工程实践中的相关数据进行概念层次划分，最终所得到的成熟概念即对应于模糊控制论域中模糊子集的语言变量，成熟概念的数目便为隶属度函数的数目。文献[13]针对现有6种形态的隶属度函数，验证了高斯型隶属度函数的普适性，据此，本文的隶属度函数便选为高斯型。从而，本文可基于自适应高斯云变换对概念进行划分，利用概念划分后得出的高斯云的数字特征指导模糊控制中高斯型隶属度函数的构建，并得出覆盖范围。

1.1　高斯云

基于高斯分布的云模型称之为高斯云，其定义如下：

设U是一个用精确数值表示的定量论域,C(Ex,En,He)是U上的定性概念,若定性值x(x∈U)是定性概念C的一次随机实现,且En′～(Ex,He2),x～(Ex,En′2),x对C的确定度满足

(1)

称x在U的分布为高斯云,如图1所示。

图1　云模型数字特征示意图

期望Ex为最能够代表定性概念的点;熵En为标准差的期望,反映了云滴的离散程度;超熵He是熵的不确定性度量。

正向高斯云算法实现了从数字特征表示的定性概念到定量的数据集合的转换,具体算法如下:

Input:数字特征(Ex,En,He),云滴个数N;

Output:云滴drop(xi,ui),i=1,2,…,N;

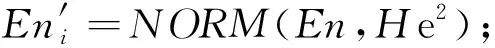
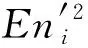
ui);

Step4重复进行Step1～3生成N个云滴。

逆向高斯云算法企图实现从一组样本数据集合去获取表示定性概念的数字特征,具体算法如下:

Input:样本点xi,i=1,2,…,N;

Step1计算样本点xi的期望值

(2)

计算样本一阶绝对中心矩

(3)

计算样本二阶中心距

(4)

(5)

Step3计算超熵

(6)

云模型正是利用上述正、逆向高斯云算法实行了定性概念数字特征(Ex,En,He)和数据样本之间的相互转换。

1.2　概念共识程度的表征与度量

隶属度函数的数目增多,控制性能显著提升的同时也会导致控制规则过多而增控制器的设计难度,但若隶属度函数数目过少,则难以对控制性能进行精心调整。如何在满足控制性能的条件下选择合理的隶属度函数数目便是一个很有意义的问题。为了确定原始样本数据对应的概念数目,本文引入概念含混度[14]以衡量概念划分过程中达成共识的程度并进一步指导概念层次划分。概念含混度的定义如下:

CD=3He/En

(7)

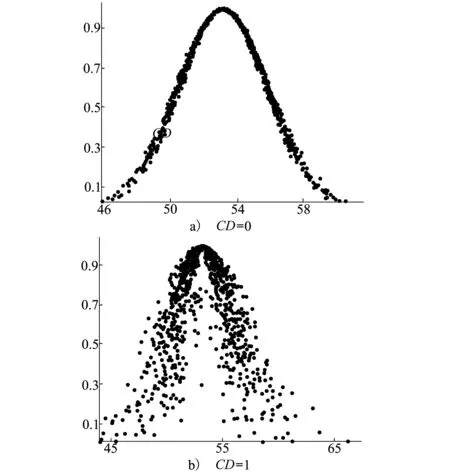
图2　概念共识云图

含混度为0,则概念外延汇聚,形成共识,是一个成熟的概念,如图2a)所示;含混度为1,则概念外延发散,难以形成共识,概念雾化如图2b)所示。表1阐明了概念含混度和概念解释之间的关系。

根据实际问题设定合理的概念含混度阈值便可引导原始样本数据生成合适的概念数目,从未可确定隶属度函数的数目。

表1　概念含混度对概念划分结果的度量标准

1.3　自适应高斯云变换

自适应高斯云变换即将任意给定的数据样本集合转换成多个用高斯云表征的定性概念以实现概念的划分,且可通过计算出的概念含混度值与预设的概念含混度阈值β之间的比较来指导优化生成概念的数目。模糊控制中确定模糊子集的过程实质便为一个基于数据样本的概念辨识过程,将定量的数据转化到定性的自然语言域。因此,利用自适应高斯云变换算法最后输出的M个高斯云所对应的M个成熟概念即为模糊控制中M个模糊子集的语言变量,如NL,PL等。

本文以正、逆向高斯云算法为基础设计自适应高斯云变换算法如下所示:

Input:数据样本集X{xi|i=1,2,…,N},概念含混度阈值β;

Output:M个高斯云C(Exk,Enk,Hek),k=1,2,…,M;

Step1统计数据样本集X{xi|i=1,2,…,N}频度分布p(xi)的波峰数量m,作为概念数量的初始值;

Step2基于概念数量的初始值m,利用高斯云混合模型算法将样本集X{xi|i=1,2,…,N}转换为m个高斯分布;

Step3对第k个高斯分布G(uk,σk),根据

uk-1+3α1σk-1=uk-3α1σk

(8)

计算左侧2个相邻概念之间不交叠的缩放比α1;根据

uk+3α2σk=uk+1-3α2σk+1

(9)

计算右侧2个相邻概念之间不交叠的缩放比α2;最终取α=min(α1,α2);

Step4计算表征第k个概念的高斯云参数:

期望

Exk=uk

(10)

熵

Enk=(1+α)×σk/2

(11)

超熵

Hek=(1-α)×σk/6

(12)

至此,则将原始样本X{xi|i=1,2,…,N}聚类为m个高斯云C(Exk,Enk,Hek),k=1,2,…,m

Step5计算概念含混度并排序

CDk=3×Hek/Enk=(1-α)/(1+α)

(13)

如果CDk>β,k=1,2,…,m,则概念数目m=m-1,跳转至Step2;否则,输出M个含混度小于β的高斯云C(Exk,Enk,Hek),k=1,2,…,M。

2　无人机模型的建立

2.1　无人机动力学模型

以某型无人机在一定高度和速度下的平飞状态为基准运动,在基本假设之下,借助小扰动法将飞机一般运动方程线性化以得到相互独立的纵向通道小扰动线性方程和横侧向通道小扰动线性方程。因无人机纵向通道和横侧向通道控制系统相似,故本文仅给出飞机纵向通道的小扰动状态方程，如(14)式和(15)式所示。

(14)

(15)

2.2　系统控制模型

本文选取俯仰角ϑ为控制量,设计其控制模型如图3所示。

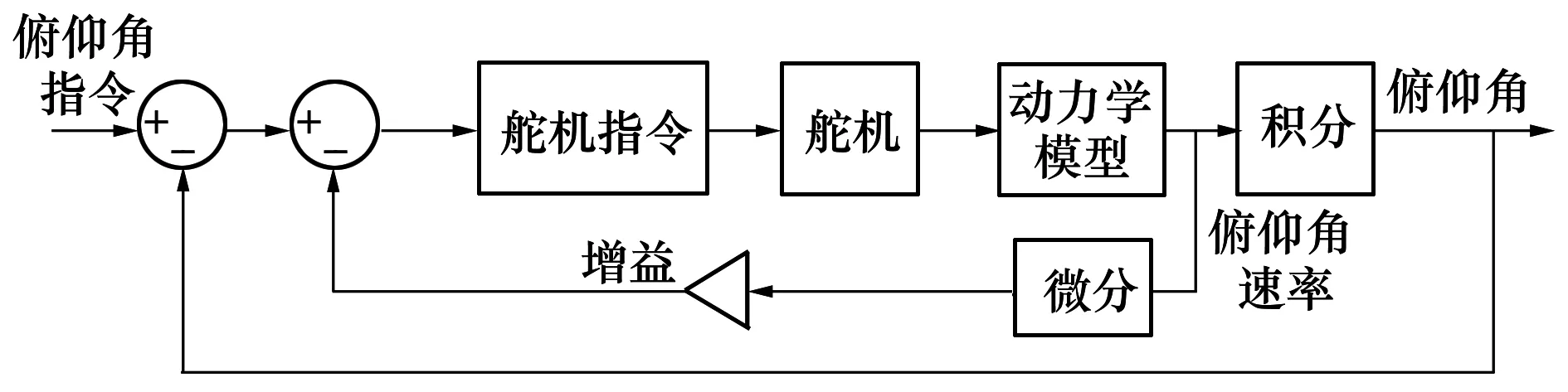
图3　俯仰角控制模型

将无人机当前俯仰角和俯仰角指令的差值作为舵机的输入量,从而控制升降舵的偏转。根据无人机动力学模型可得到俯仰角速度变化值Δϑ,经过积分环节之后即可得到俯仰角的变化值。模型中引入了微分环节,其作用是借助俯仰角速度的反馈以增加短周期模态阻尼。舵机近似于一个惯性环节,传递函数可表示为

(16)

式中,kδ为静态增益;Tδ为时间常数。

3　模糊控制器的设计

图4　模糊控制simulink仿真图

3.1　输入量和输出量的标准化

本文采用如(17)式和(18)式所示方法将输入量和输出量映射到所需范围。

(17)

(18)

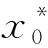
3.2　模糊控制规则及模糊蕴含

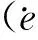
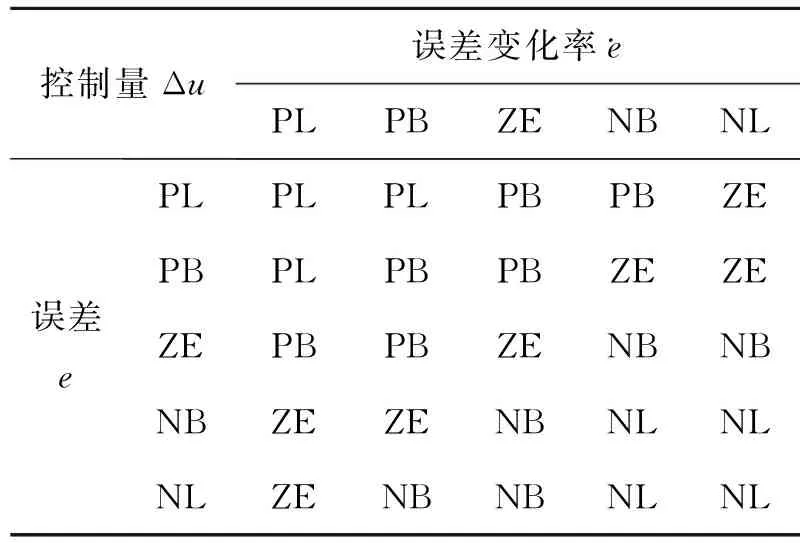
表2　俯仰角模糊控制规则表

模糊蕴含是指确定模糊规则的前提部分对结论部分产生的影响的一种措施,本文设置为And Method=min, Or Method=max, Implication Method=min, Aggregation Method=max。

3.3　清晰化计算

清晰化计算是指将模糊推理得到的模糊量利用算法转化为控制所需的实际量。本文采用适应于输出隶属度函数为对称函数的面积重心法,其计算公式为:

(19)

式中,ej和μcj(ej)分别代表隶属度函数的质心和隶属度函数数值。

4　仿真验证

4.1　隶属度函数的提取

根据无人机控制的工程实践样本数据,对实际控制过程中出现的俯仰角误差值进行800次提取后其所得的数值频度分布如图5所示。

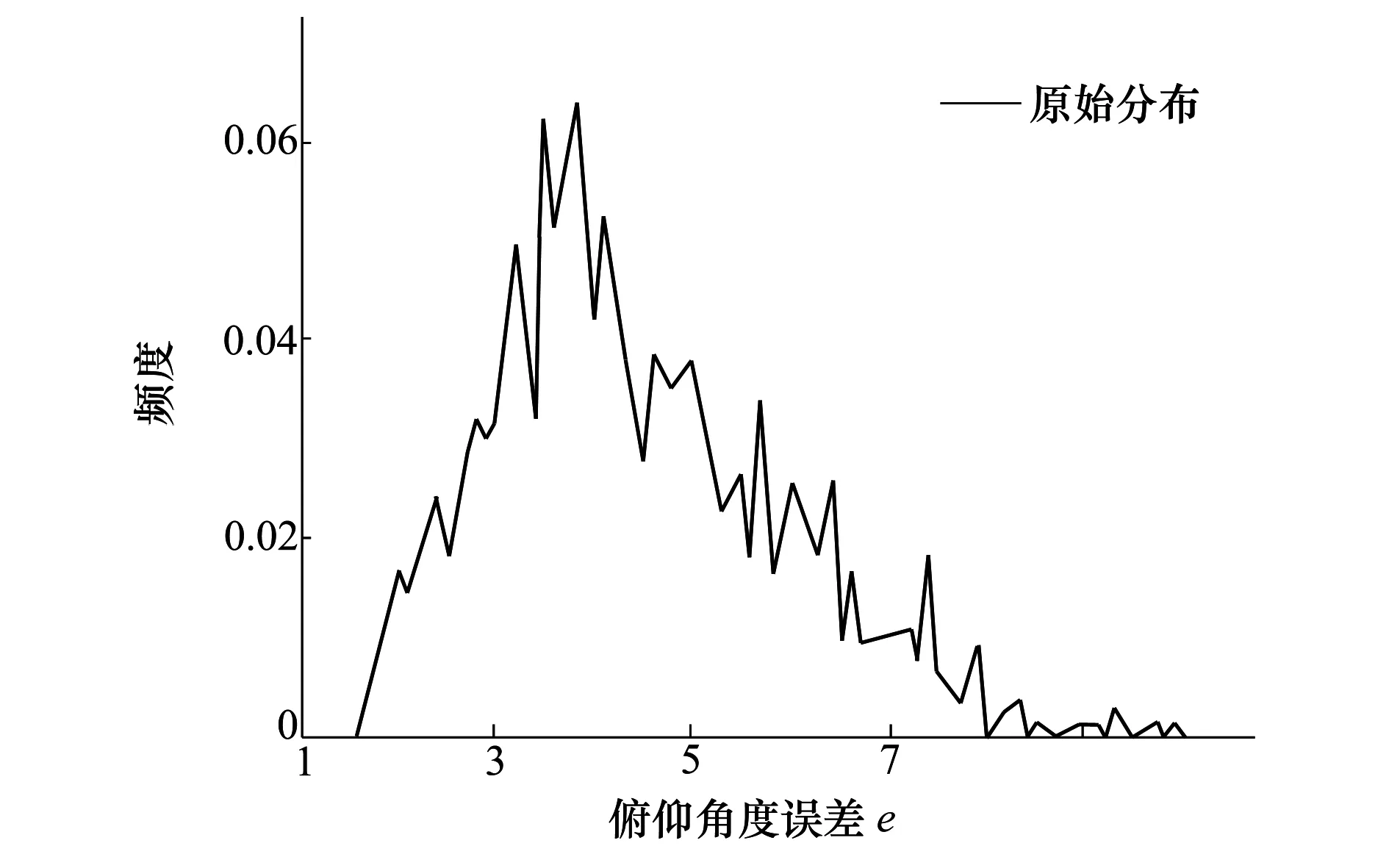
图5　俯仰角角度误差数据频度分布图

由图5可知原始数据峰值高达23个之多,数据频度曲线抖动严重。利用高斯云变换对俯仰角误差数据进行高斯云变换之后,初步可得到12个模糊概念,如图6所示。从中可看出,由高斯云变换得到的与初始概念相对应的12个高斯云的叠加基本上反映了实际数据的分布情况。

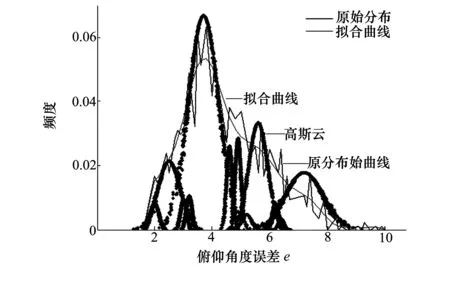
图6　12个初始概念的高斯云图

由图6可知12个初始概念存在骨干区交叠的情况,由表1可知,概念含混度较高,概念划分混乱,需要进一步减少概念数目。设定概念含混度上限为β=0.17以指导自适应高斯云变换,得到包含7个概念的高斯云图如表3和图7所示。

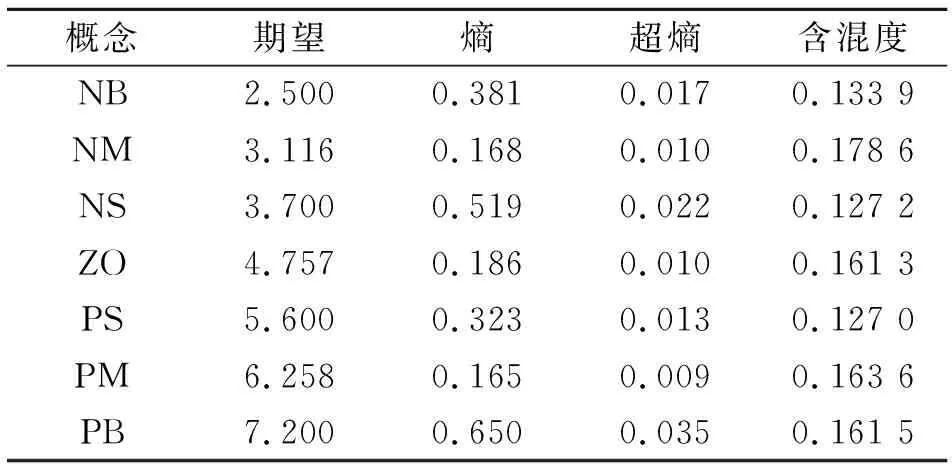
表3　7个概念的数字特征

语言变量NM的概念含混度β=0.178 6>0.17,大于阈值,概念划分仍不够明确,需进一步减少概念数目。在满足含混度阈值β=0.17的情况下最终得到如表4和图8所示的包含5个概念的高斯云图。

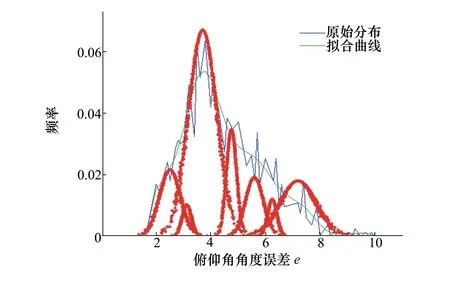
图7　7个概念的高斯云图

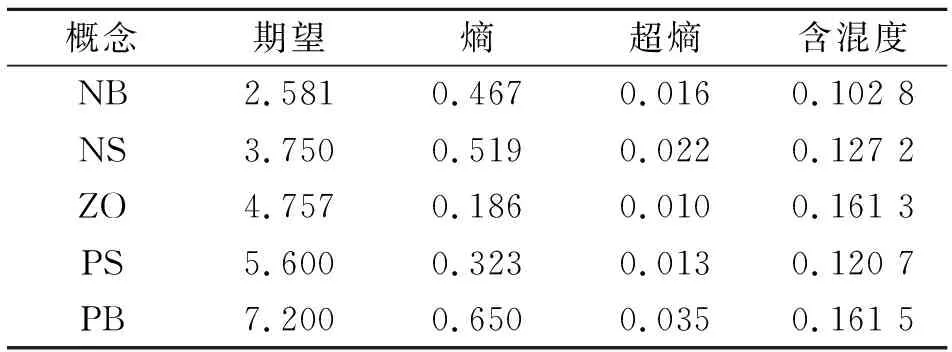
概念期望熵超熵含混度 NB2.5810.4670.0160.102 8 NS3.7500.5190.0220.127 2 ZO4.7570.1860.0100.161 3 PS5.6000.3230.0130.120 7 PB7.2000.6500.0350.161 5

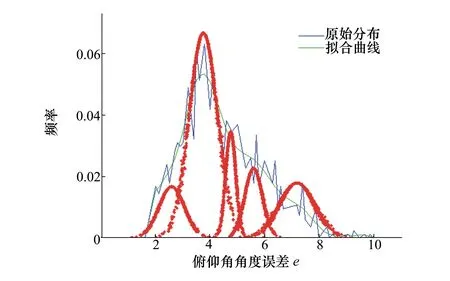
图8　5个成熟概念的高斯云图

上述通过自适应高斯云变换对俯仰角角度误差进行聚类的过程是从23个初始概念(原始数据的峰值数)到5个成熟概念的提升过程,从概念含混度较高,高斯云交叠严重到满足概念含混度阈值形成成熟概念。

4.2　模糊控制

以某型无人机在高度1 000 m,速度40 m/s下配平可得到(15)式中的Ax矩阵和Bx矩阵如下:

Ax=

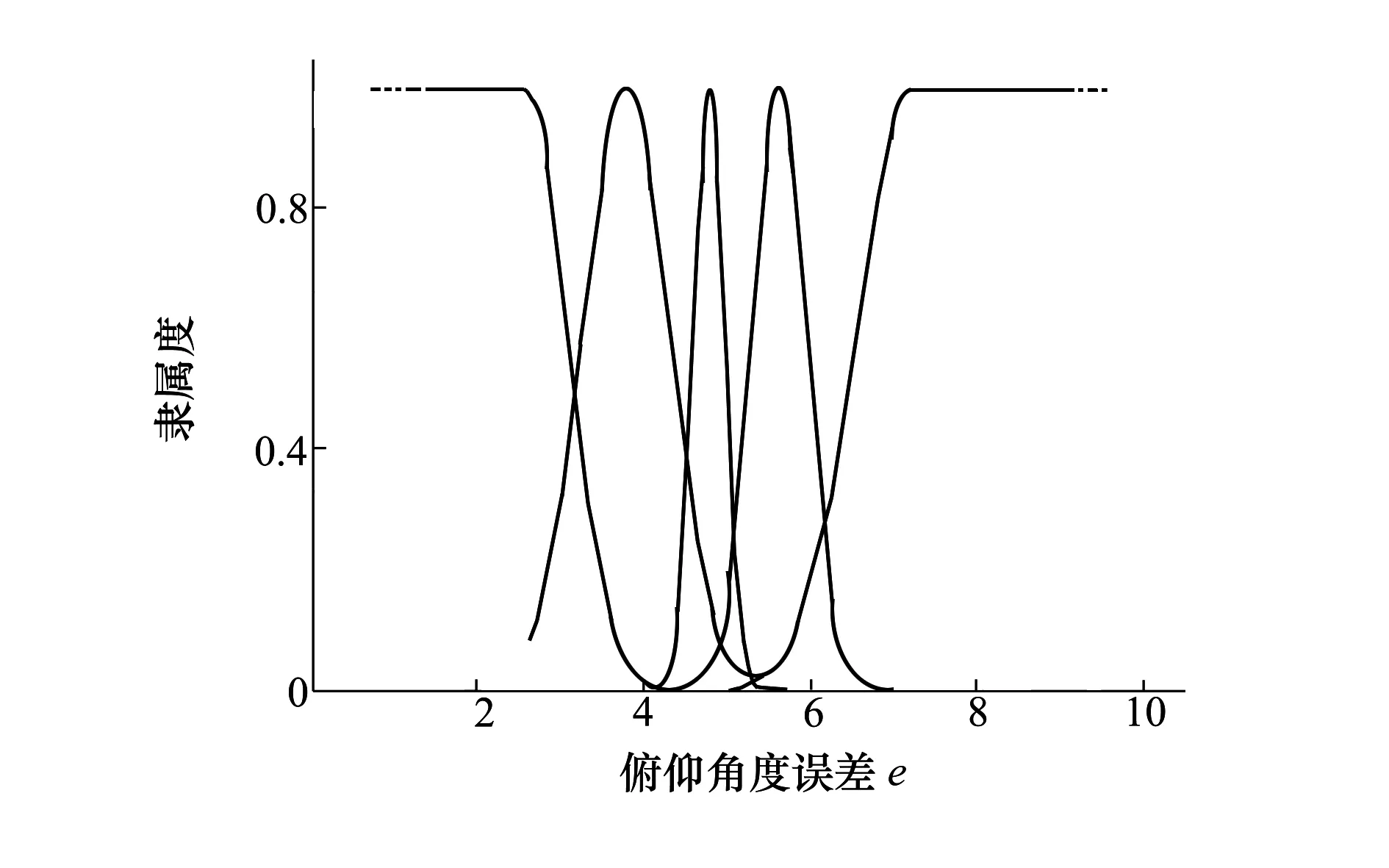
图9　俯仰角误差隶属度函数

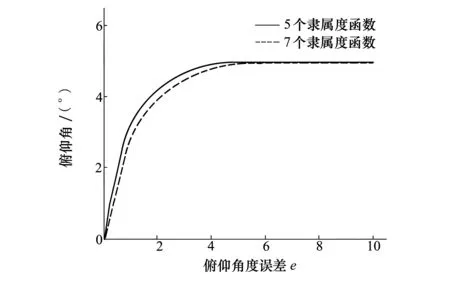
图10　隶属度函数数目不同的俯仰角模糊控制图

由图10可知，利用自适应高斯云变换所提取的隶属度函数可有效实现无人机俯仰角的控制，达到预期的角度值，验证了此种方法选取的隶属度函数的有效性。仿真进行10次，分别求取5个隶属度函数和7个隶属度函数情况下所对应的上升时间的均值，结果如表5所示。

表5　隶属度函数数目不同下的性能比较

由表5可知5个隶属度函数下的控制效果稍逊于7个隶属度函数下的控制效果，结论符合模糊控制规则越多，其体现的专家经验越丰富，则控制器的性能越优越的直观思想。但是模糊控制器若选取5个隶属度函数，在控制性能相差不大的情况下，控制规则将会从49条减少为25条，极大简化了模糊控制器的设计。由此可知，合理的选择概念含混度上限 可在最简化模糊控制规则数目的同时保持良好的控制性能。

以表4数据所得的5个隶属度函数为基准，改变每条隶属度函数的覆盖范围。“覆盖范围不变”是指每条隶属度函数的覆盖范围均与表4数据所代表的相一致，“覆盖范围收缩”是指每条隶属度函数的覆盖范围在表4数据的基础上左右各收缩0.25，论域下界和上界的隶属度函数仅单方向收缩0.25；“覆盖范围延伸”是指每条隶属度函数的覆盖范围在表4数据的基础上左右各扩大0.25，论域下界和上界的隶属度函数仅单方向扩大0.25，最终所得无人机俯仰角在模糊控制器下变化曲线如图11所示。

图11　隶属度函数覆盖范围不同的俯仰角模糊控制图

由图11可知，隶属度函数的覆盖范围变化之后，仍可有效实现无人机俯仰角的控制，最终达到预期的角度值，但是不同覆盖范围的隶属度函数所对应的控制性能却不同。将上述仿真进行10次，分别求取在隶属度函数数目为5但覆盖范围不同的情况下所对应的上升时间的均值，结果如表6所示。

表6　覆盖范围不同下的性能比较

由表6可知，利用自适应高斯云变换算法所确定的隶属度函数的覆盖范围相比于随意设定的情况，可有效提高模糊控制器的控制性能。

5　结　论

本文为了推动模糊控制在工程实践中的应用，针对模糊控制器设计过程中隶属度函数的选取问题，基于自适应高斯云变换算法提出了一种通用型隶属度函数的选取方法以确定模糊控制器中隶属度函数的数目、形状及覆盖范围。隶属度函数形状选为高斯型，利用自适应高斯云变换算法对原始数据进行概念层次划分后最终所得到的成熟概念即对应于模糊控制论域中模糊子集的语言变量，成熟概念的数目便为隶属度函数的数目，高斯云的分布情况即可确定出隶属度函数的覆盖范围。仿真结果表明利用自适应高斯云变换算法所确定的隶属度函数嵌套于模糊控制器之后可实现良好的控制性能，具有较好的动态特性。