塔机双吊点起重臂力学模型及实验验证

杜 波 刘 垚 钟胜伟 殷 鹰

（四川省特种设备检验研究院 四川成都 610061 ）

引 言

在塔机设计计算过程中，首先需要建立主要受力部件力学模型，并对其进行力学分析，力学模型建立的正确与否，将关系到计算结果的正确性。很明显，受力部件的力学模型与结构实际受力情况越吻合，计算结果就越准确、可靠。双吊点塔机是一种常见的塔机种类，其主要受力部件有起重臂、平衡臂、塔帽、塔身。其中，双吊点起重臂属于超静定结构，力学模型不易准确建立；而平衡臂、塔帽和塔身属于静定结构，其模型易于建立，由于篇幅有限，这里不做介绍，本文主要对双吊点起重臂的力学模型进行分析和实验验证。

1 双吊点起重臂力学模型

1.1 起重臂两拉杆内力计算

目前，双吊点起重臂采用刚性拉杆的支承形式比较普遍，计算分析的关键是迅速而正确地求出两拉杆的拉力，通常采用力法进行求解。具体方法是将一根拉杆切断并代之以多余约束力得到基本静定结构，并根据起重臂结构的变形条件建立变形协调方程(力法方程)，求解出基本未知数(即多余约束力)。在以往解此超静定结构时，力法方程中的位移量δ11、△1q和△1p只考虑了起重臂拉杆的轴向变形和起重臂架的弯曲变形[1]，由于臂架受压段(OB段)的轴心力较大，而臂架的整体截面积和起重臂拉杆的截面积相比又不是大出很多倍，因此作为压弯构件的起重臂，在轴心力影响下的轴向变形也应考虑到力法方程的位移计算中去，这样比解超静定组合结构的一般方法更为全面和精确。

当采用力法求解图1所示的计算模型时可得如下公式：

式中：

δ11—柔度系数，即单位未知力(R1=1)单独作用时引起的短拉杆的轴向位移；

R1—短拉杆拉力；

△1q—起重臂自重和变幅机构自重作用下短拉杆的轴向位移；

△1p—吊重 作用下引起的短拉杆的轴向位移。

对上式进行整理可得：

从式②可以看出，只要计算出δ11、△1q和△1p，就可以求出短拉杆的拉力，再进一步求出长拉杆的拉力。显然△1q、△1p和δ11三个未知数的求解方法是方程②求解的关键。

图1 双吊点起重臂力学模型

（1）计算柔度系数δ11

图2为将短拉杆切断解除多余约束所得到的基本结构。将该拉杆的拉力用R1=1的单位力代替。在计算模型中，由∑M0=0，可得单位力作用下长拉杆的拉力：

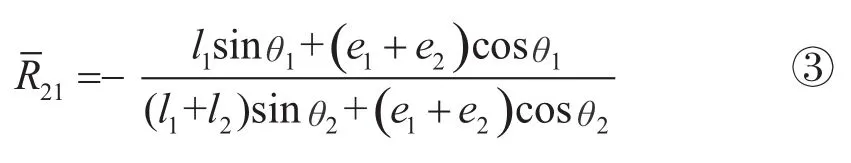
求出各主要点处的弯矩和轴力，绘制出起重臂结构在单位力单独作用下的弯矩图和轴力图，如图2所示，采用图乘法即可求出柔度系数δ11，如公式④。

图2 单位力单独作用下臂架受力分析

（2）起重臂自重和变幅机构自重作用下短拉杆的轴向位移 △1q

图3为起重臂自重和变幅机构作用下臂架的受力分析。由于起重臂各臂节重量不一定相同，分别将OA、AB、BC段的臂节重量加权平均化处理。由∑M0=0，可得自重集度和变幅机构自重作用下长拉杆的拉力R2q：

求出起重臂的弯矩和轴力，绘制出起重臂结构在自重均布力和变幅机构自重作用下的弯矩图和轴力图，如图3所示。采用图乘法可求出短拉杆的轴向位移△1q，如公式⑥。

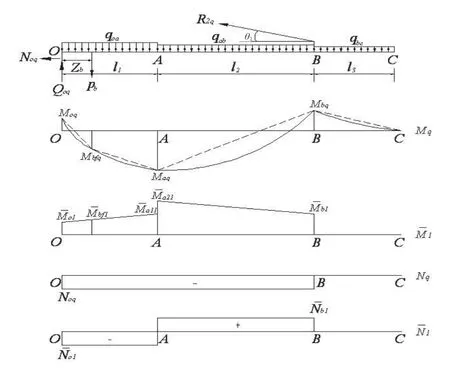
图3 自重和变幅机构作用下臂架受力分析

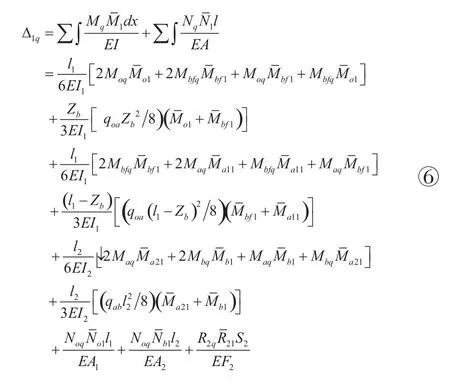
（3）吊重P作用于吊臂BC段引起的短拉杆的轴向位移△1p

图4为吊重在BC段时臂架的受力分析。由∑M0=0，可得吊重作用下长拉杆的拉力：

求出起重臂弯矩和轴力，绘制出起重臂结构在吊重单独作用于吊臂BC段的弯矩图和轴力图，如图4所示，采用图乘法可以求解出短拉杆的轴向位移△1p，如公式⑧。

图4 吊重在BC段时臂架的受力分析

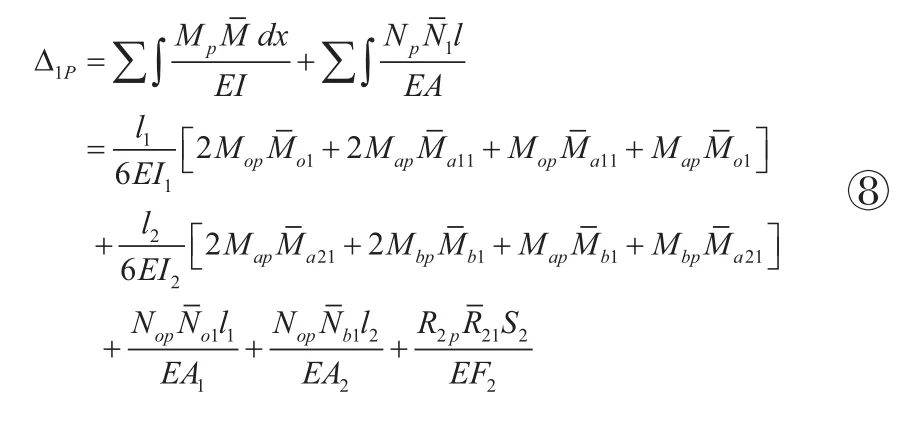
将④、⑥、⑧分别代入②中即可求出R1，并由式可得长拉杆的拉力R2。当吊重位于起重臂OA和AB段时，其计算方法与吊重P作用于起重臂BC段相同，只是内力图不同。

1.2 危险截面强度计算

计算出两拉杆的拉力后，就可以绘出起重臂的内力图，计算起重臂危险截面处的应力。两拉杆主要承受拉力，其应力计算公式为σ=N/A；而起重臂属于压弯组合构件，根据材料力学的知识[2]，可以得出其危险截面处强度计算公式：

2 实例验证

为验证上述力学分析模型，编写了塔机计算机辅助设计软件TowerCrane3.0。并对某QTZ4511型塔机进行静应力校核计算，将计算的结果与该型号塔机的静应力测试报告上起重臂危险点处的应力测试结果相比较，测点根据结构受力分析在危险应力区选择确定，该型号塔机起重臂部分应力测试布点如图5所示。为了与实际测试情况相符合，采用软件计算时不考虑风载、回转、冲击载荷的作用。测试按四个工况进行，各工况下额定载荷和加载幅度为：工况一：Q＝1.1 t，R＝45 m；工况二：Q＝2.4 t，R＝24.2 m；工况三：Q＝4 t，R＝7.28 m；工况四：Q＝4 t，R＝15.4 m。

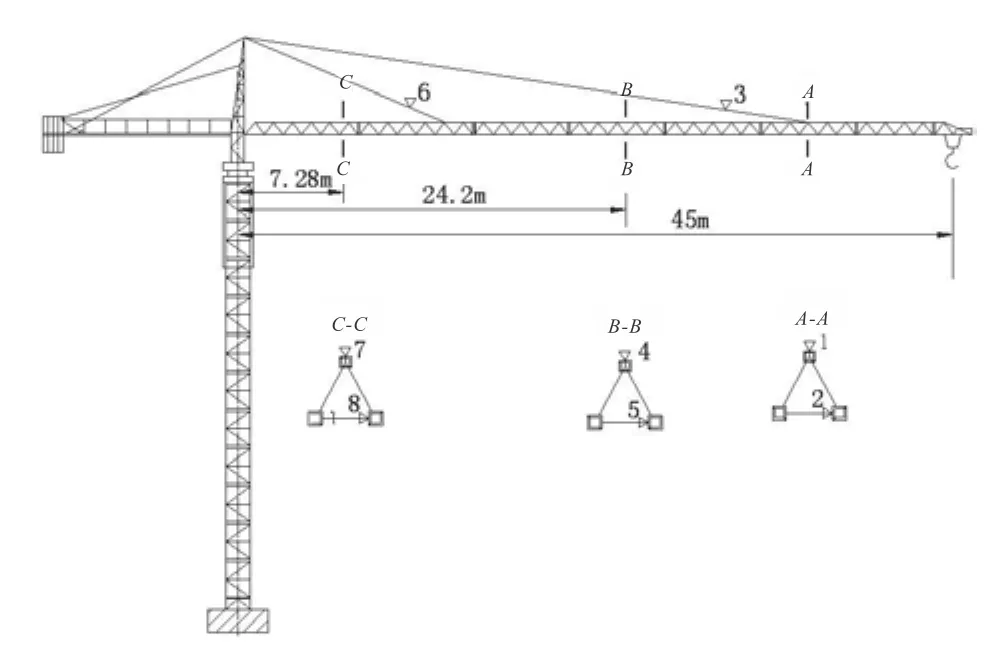
图5 塔机起重臂应力测试布点图

各测点计算应力与测试应力如表1所示。

表1中，规定拉应力为正，压应力为负。由于测试中难以测得起重臂自重应力Q0，通常均由计算得到。Qf是将测试载荷施加到相应工况下的相应幅度之后各测点应力变化值，故起重臂自重及载荷共同作用下测点的应力为：Qr＝Q0＋Qf。表中的Qs为采用上述计算软件得到的计算应力。

表1 起重臂各测点处应力对比 / MPa

对以上表格中的数据进行分析，可得出如下结论：

（1）在实验中，起重臂最大拉应力出现在测点3处，最大压应力出现在测点4处，计算应力也在相应测点处为最大值，两者结果具有一致性。并且测试与计算结果的相对误差分别为8.68%和5.3%，计算结果与测试结果比较接近。起重臂上测点的相对误差在5%～7%之间，两拉杆测点的相对误差在7%～8.7%之间，分析其原因是在计算中忽略了刚性拉杆自重对起重臂计算的影响[3]，同时，将起重臂自重作加权平均化处理，带来了一定的误差。

（2） 以上各测点的相对误差均9%以内，对于理论计算，还是可以接受的。实验结果与塔机起重臂结构理论分析计算结果还是比较符合的。从而也就说明了塔机双吊点起重臂力学计算模型以及程序设计具有一定的正确性和可靠性。

3 结 论

（1）运用结构力学知识，建立了塔机双吊点起重臂超静定结构的静力学模型，推导出起重臂内外拉杆所受拉力的计算公式和危险截面的强度计算公式。

（2）将理论计算结果与实验结果进行对比，相对误差均9%以内，验证了所建力学模型的正确性。

编辑：殷 鹰