Spike-Stall of Compressors-A Critical Review

Hua Chen

（Dalian Maritime University,Dalian,China）

Abstract：Spike-stall is a fast stall mode of both axial and centrifugal compressors.It can very quickly lead to surge and interrupt the normal operation of compressors.Despite decades’efforts,we still do not have a clear picture of how it starts and develops,let alone predicting it.This paper reviews the research works on this instability of compressors,describes the progress made,discusses the shortcomings of current research,and proposes some new concepts that may lead to breakthroughs.It is pointed out that current methods of predicting spike-stall are mostly based on classic stability concept which is incapable of handling the transient growth and diminution of disturbances in short length scales that typify spike-stall.Modern transient instability concept is proposed that establishes the link between the maximum amplification of the system to initial perturbations and time.The non-normality of compressor system is also emphasised.

Key Words：Compressors,Spike-stall,Transient growth,Non-normality

Nomenclature

BFVBack flow vortex

G(t) Optimum energy amplification to initial conditions

LELeading edge

PPressure(N/m2)

TETrailing edge

TLVTip leakage vortex

TSVTip secondary vortex

UBlade speed(m/s)

URANSUnsteady Reynolds averaged Navier-Stokes eqns.

rDensity(kg/m3)

WAngular speed of shaft(radian/s)

ωzAxial vorticity(radian/s)

Subscripts

tTotal,blade tip

vlsVaneless space

1　Introduction

Flow instability is a common problem for compressor.Surge for example is a typical instability of compressors which limits the flow range of compressors.Surge itself is usually triggered by stall.There are at least two types of stall that are now well known,and they are modal-stall and spike-stall.Modal stall is characterised by disturbances in a length scale of impeller periphery or so,and it typically takes tens to hundreds of impeller revolutions to develop from inception to a full scaled instability.The theory of modal stall is relatively mature,and the general topic of modal-stall inception and active control has been discussed in[1-3].

The spike-stall on the other hand is characterised by spike type disturbances of short length scales typically starting in one pitch and developing in a few.Its progress is much faster than modal-spike and it usually only takes a few rotor revolutions to grow from the initial spike to a full scale of rotating stall[3].Figure 1,taken from[3],shows modal-stall and spike-stall at two rotors respectively inside a multi-stage axial compressor.

In centrifugal compressors spike-stall was also observed.Figure 2 gives an example.Spike-stall often occurs in modern highly loaded compressors and at high speeds. Because of its damage to compressor performance,spike-stall has drawn much attention of compressor research in the last few decades,and many progress has been made.However,due to the apparent suddenness of the stall, many questions remain unanswered.In the remaining of this paper,we review the achieved progress and point out the areas where research attention may be focus on.Above all,a new approach based on modern fluid dynamics is proposed.

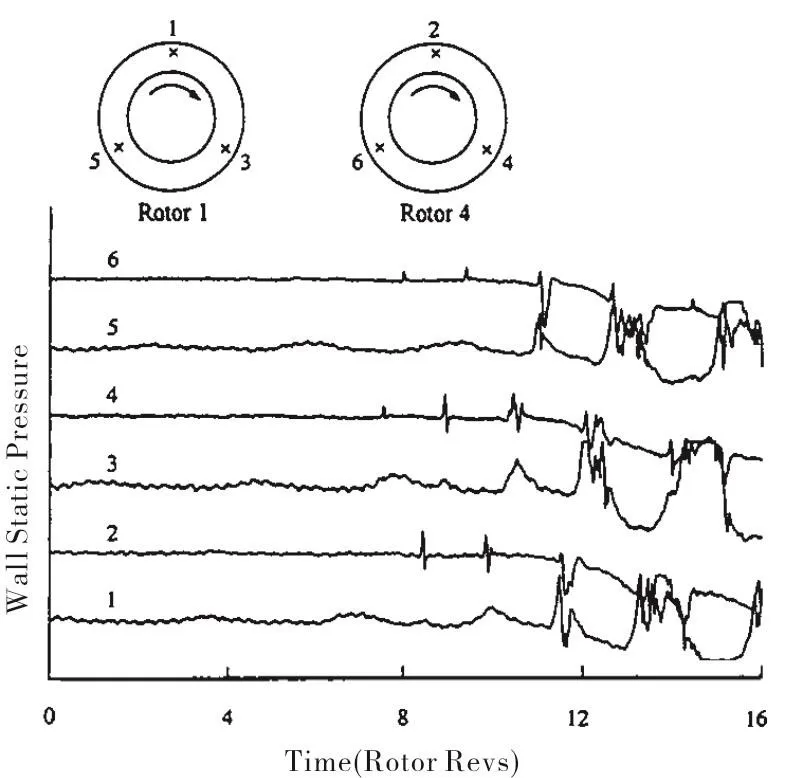
Fig.1　Wall static pressure measurement showing inception of modal-stall in Rotor 1 and spike-stall in Rotor 4.[3]

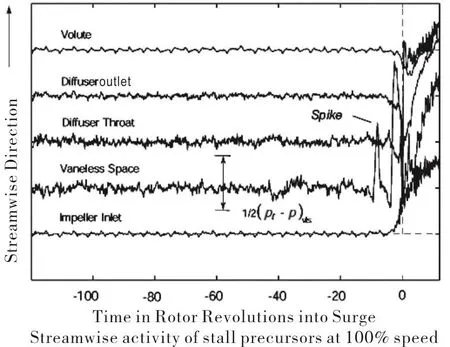
Fig.2　Spike-stall in a turbocharger compressor with vane diffuser.Spike was first observed in vaneless space upstream the diffuser inlet[4].

2　Origins of Spike-stall

2.1　Axial Compressors

There are several different versions of how spike is first generated and developed into a rotating stall.For axial compressor rotor with small blade tip-casing clearance,some authors[5-6]argued that the spike is caused by a flow separation from blade suction surface.Figure 3 illustrates this mechanism.

A positive feedback mechanism for rapid development of spike-stall can be seen from Figure 3:blockage from the separation on one blade increases the incidence on to the next,causing the next blade to separatesevererhencecreatingalargerblockage,andsoon.

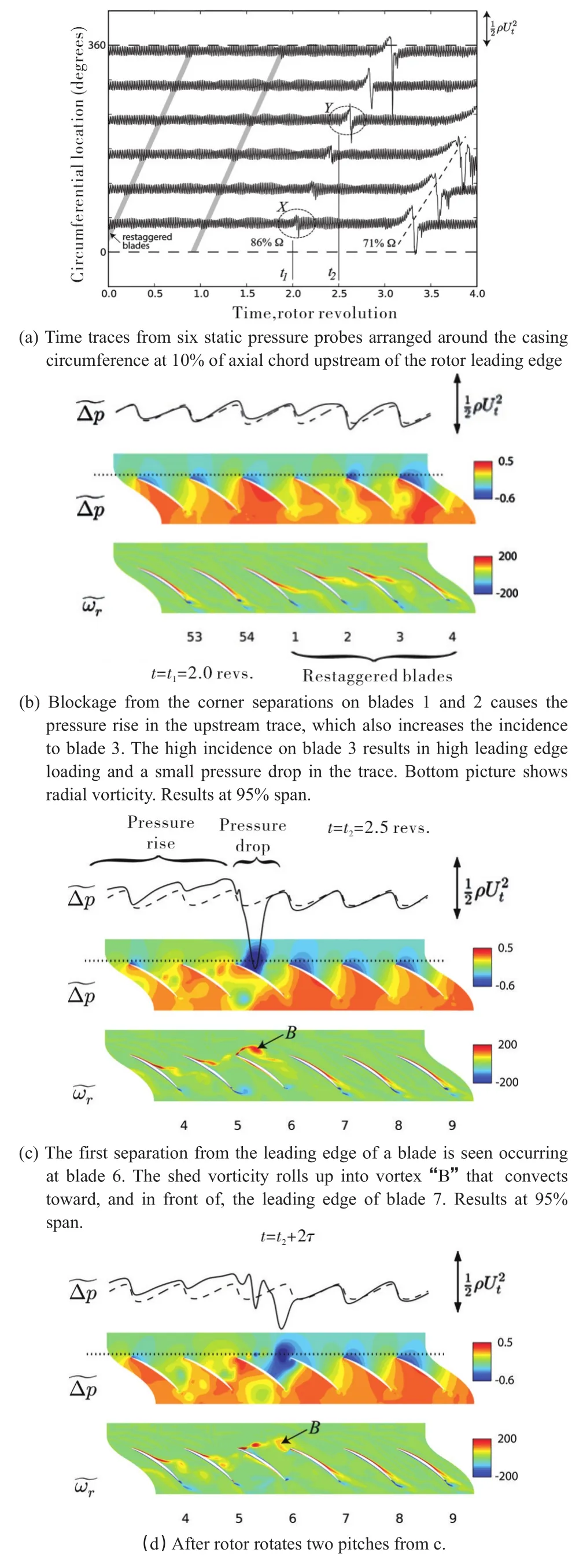
Fig.3　URANS simulation results of NASAE3 Rotor B without tip clearance,showing spike-stall inception[5].

When sizable tip clearance exists,the function of suction surface separation in stall inception is replaced by tip leakage vortex(TLV)according to[5].When a compressor is throttled toward stall,the incidence angle increases,and blade loading builds up near leading edge.The tip clearance then enables overtip leakage flow from pressure side to suction side,forming TLV,Figure 4.

Fig.4　Computed vorticity showing TLV and its breakdown at near stall but stable condition[6].

It was argued by Pullan et al[5]that in approaching stall,the TLV trajectory becomes tangential and the TLV breaks down into fragments.When the TLV reaches the neighbouring blade's leading edge,leading edge flow separation occurs due to the incidence angle change brought about by the TLV,see Figure 5.

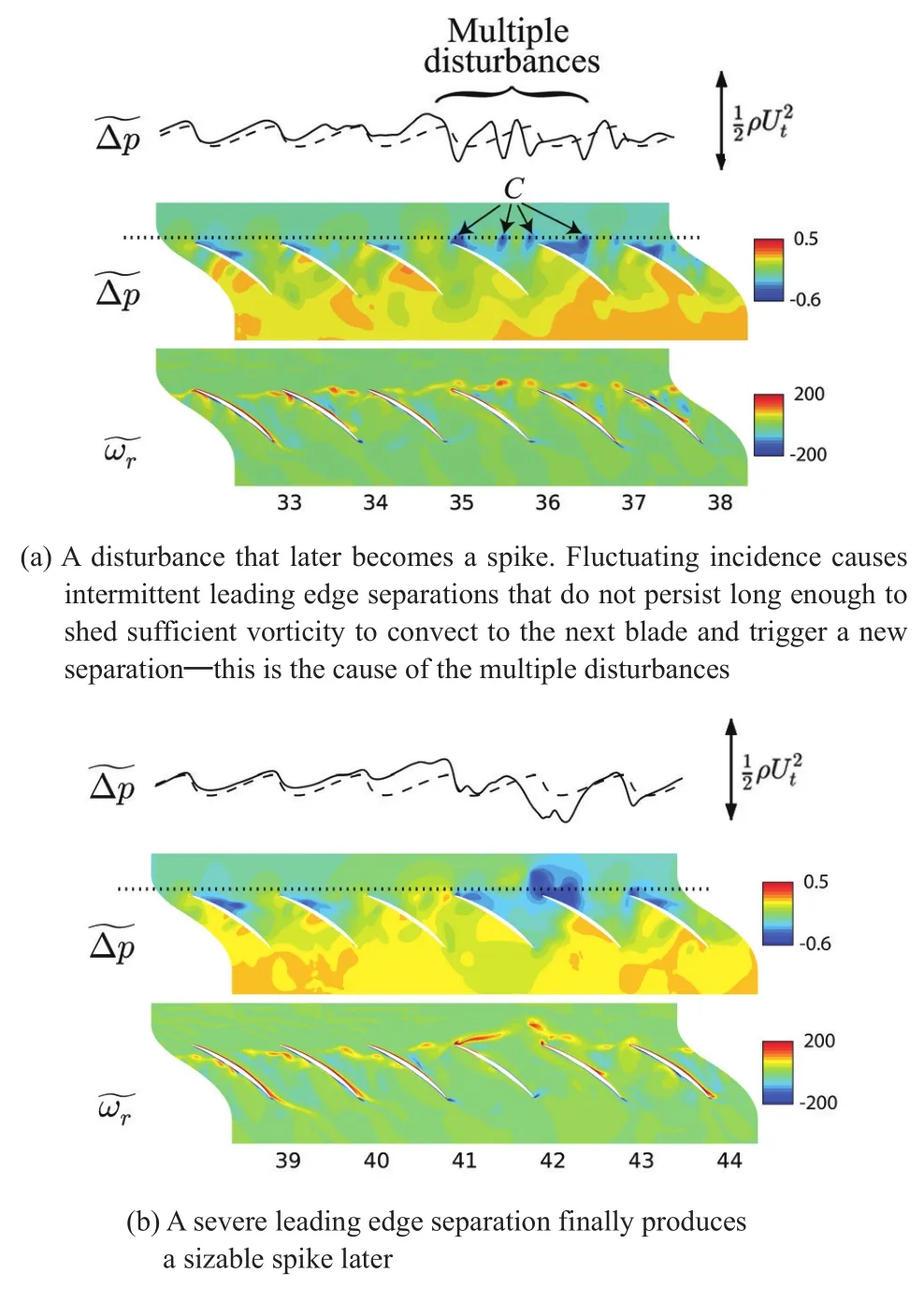
Fig.5　URANS simulation results of NASAE3Rotor B with tip clearance,showing spike-stall inception[5].

However,there are other versions of spike-stall inception. Based on stereoscopic particle image velocimetry(SPIV)and flow visualisation,Katz et al.[7]found back flow vortices or BFV induced by TLV,as shown in Figure 6.In a further work[8]they proposed that it is the tangential movement of the BFV that triggers the flow separation of next blade which starts a spikestall,as it can be observed in Figure 7.

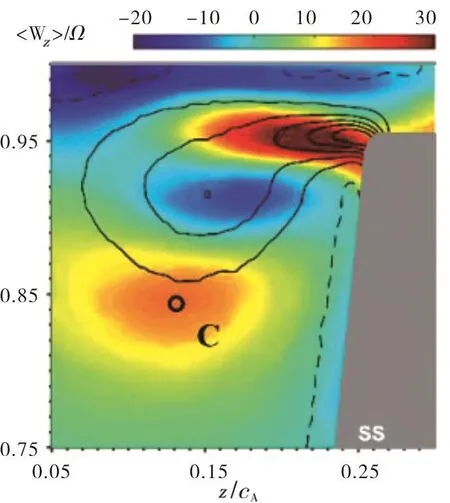
Fig.6　SPIV measured TLV(centred at 0,blue)and BFV(centred at O,orange).[7]

Wu et al.[9]suggested a tip second vortex(TSV)mechanism,as illustrated in Figure 8.With additional instrumentation and careful planning and measurement,Weichert and Day[10]suggested that a spike is the result of the destabilization of the boundary between the incoming and reversed flows,a shear layer in tip gap,as depicted in Figure 9.TLV spillage happens later.In the figure,the TLV trajectory,which follows the interface,is still within the flow passage 14-15,while disturbances already occur at the most unstable passage 15-16.Shear layer instability is a typical flow instability,and shroud or tip clearance could provide a passage forflow disturbancesto propagate from one blade passage to another.So Weichert and Day offered a different mechanism of spike-stall inception.This version of spike-stall inception agrees with the numerical results of Haz and Katz et al[11].in which casing boundary layer was found separated but no TLV breaking down was discovered.

Fig.7　Atime sequence of cavitation images showing the propagation of vortical structures at pre-stall conditions.Arrows of same styles follow the evolution of the same backflow vortex.White lines indicate the blade tip profile.[7]

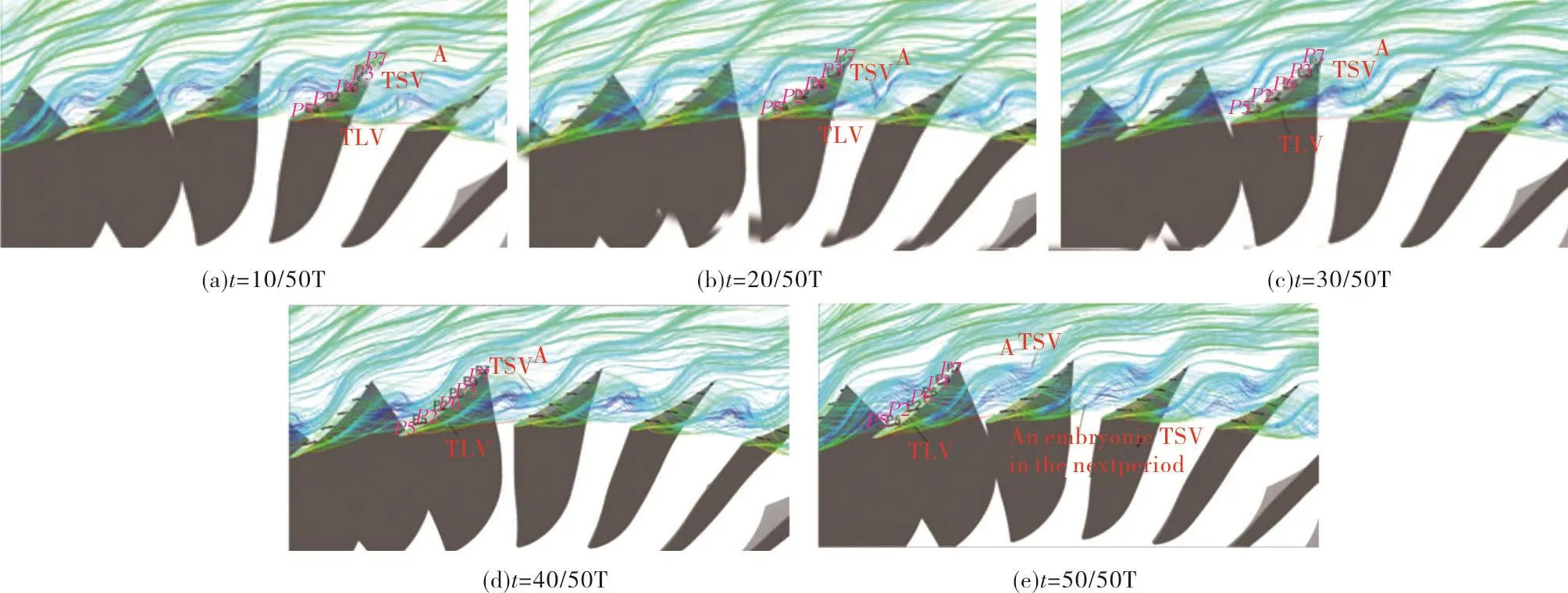
Fig.8　URANS results showing development of TSV at near stall condition.TLV is also marked.

Fig.9　Hot wire measurement of absolute flow velocity at 50%tip gap of a high speed axial compressor during embryonic spike formation.Disturbances are circled by red.

2.2　Centrifugal Compressors

There are less in depth studies of spike-stall in centrifugalcompressors.Spakovszky and Roduner[4]reported spike-stall in a marine turbocharger compressor.The stall was first observed at vaneless space between impeller trailing edge and vane diffuser leading edge,at 100%speed,see Figure 2.Everitt and Spakovszky later[12]proposed a mechanism for this stall based on numerical evidence,as portrayed in Figure 10.

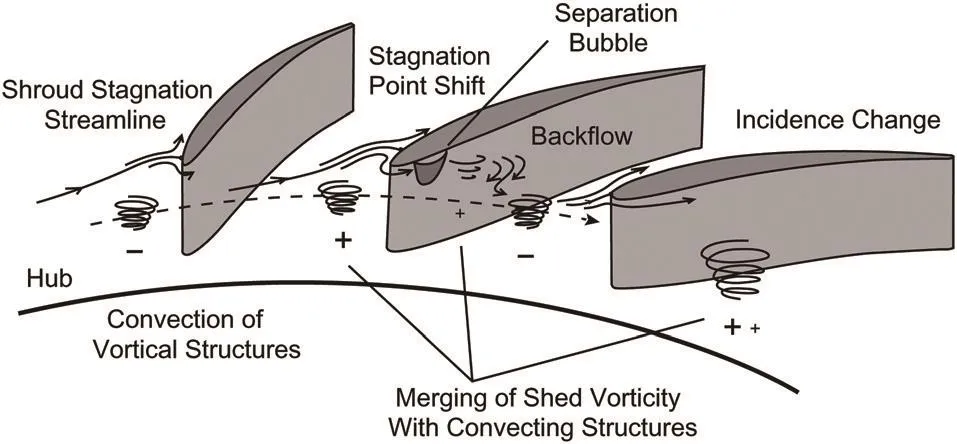
Fig.10　Spike-stall mechanism proposed by[12]

According to[12],separation at the diffuser leading edge caused by high incidence near the shroud endwall sheds vorticity from the diffuser vane leading edge.Locally reversed radial flow in the vaneless and semivaneless space then allows the vorticity to convect back to the vaneless space.The flow in the vaneless space that recirculates around the circumference allows the vortical structures to form and to grow through the addition of new vorticity shed from the diffuser vane leading edge;and a feedback mechanism whereby the convection of the vortical structures within the developing stall precursor triggers a variation of incidence on the downstream blade,such that further vorticity/low total pressure fluid sheds from that vane and causes growth of the precursor.

Buffaz and Trébinjac[13]measured casing pressure signals of a high speed centrifugal compressor and concluded that when the compressor is in rotating stall,the TLV from one blade reaches the front part of the inducer,as depicted in Figure 11.Note that in the figure,the TLV is not parallel to the tangential direction.

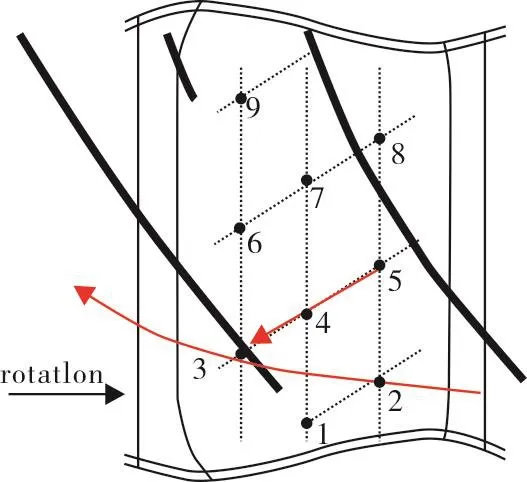
Fig.11　Sketch of trajectories of TLV(broken red line)and overtip leakage flow(solid red line from 5 to 3)in rotating stall of a helicopter compressor,based on casing pressure signals from transducers 1-9[13].

In centrifugal compressors with vaneless diffuser,such as the compressors for road vehicle turbochargers,modal type of stall is often reported before surge[14].However,at high speeds,transition to surge can be very abrupt and without modal wave precursor.Vaneless diffuser stall is considered to trigger the surge under this speed condition.More work is required to establish if spike-stall exists in vaneless diffusers.

2.3　Two Conditions for Spike-stall

Based on numerical simulation results,Vo and others[15]proposed a two-conditions criterion for spikestall inception in axial compressors,that is,the TLV or the interface between approaching flow and tip leakage flow reaches the LE of the adjacent blade,and reverse flow occurs at the TE.For centrifugal compressors,often the first condition was quoted in literature when rotating stall happens.

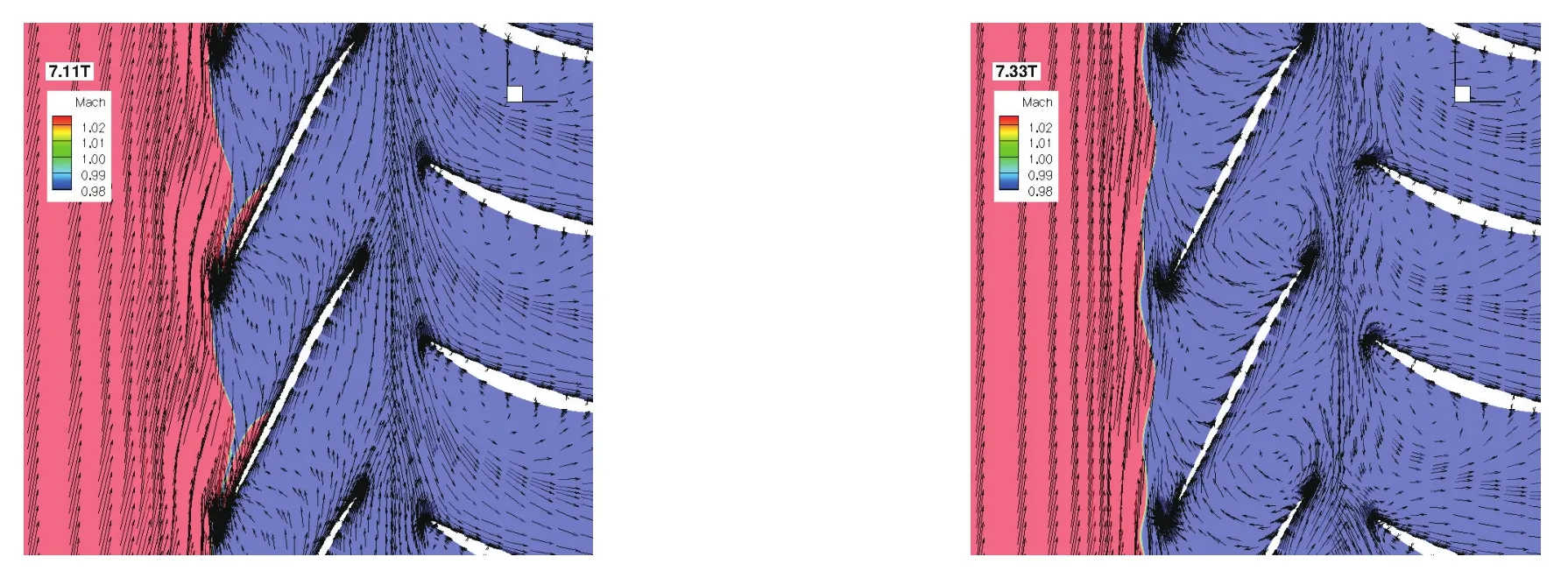
Fig.12　Calculated relative Mach number and flow velocity vectors at blade tip of a transonic axial flow compressor just before(left)and at stall(right)[16].

From the discussion in 2.2,we know that the first condition is open to questions,and is perhaps the consequence of another flow instability that really starts the spike inception.The second condition is illustrated here in Figure 12 for a transonic axial compressor[16].In the graph shown on the right,reversed flow can be seen.However,the stator is already stalled before the stage stalls as can be seen in the graph on the left.The separation of the stator on the suction surface creates a throttling effect on the rotor,forcing the latter to stall.So,the trigger of the spike-stall in this case is the stator and not the rotor,just like in the case of centrifugal compressors.

In the vaneless diffuser used in centrifugal compressors,reversed flow reaching diffuser exit was found to be the condition of diffuser stall[17].

3　Prediction of Spike-stall

Predicting compressor instability is always a difficult task,forecasting spike-stall is even more challenging because of the short time scale within it can develop.Here some attempts are reviewed.

3.1　Semi-empiricalMethods

While the first condition of spike-stall proposed by Vo et al[15],the TLV reaches theLEof adjacent blade or becomes parallel to tangential direction,may not be precise,it offers a convenient way to predict spike-stall empirically.Cameron and Du et al[18]proposed a stall prediction method based on this condition.From experimental and numerical results,they found that this condition is equivalent to the state when the line of zero casing wall shear stress reaches theLEof a neighbouring blade.Applying the axial momentum conservation to the clearance flow and main flow,an empirical model was built to establish the compressor operating condition that leads to stall,see Figure 13.The model contains two empirical coefficients that are compressor specific and may be fixed by experimental or CFD results.

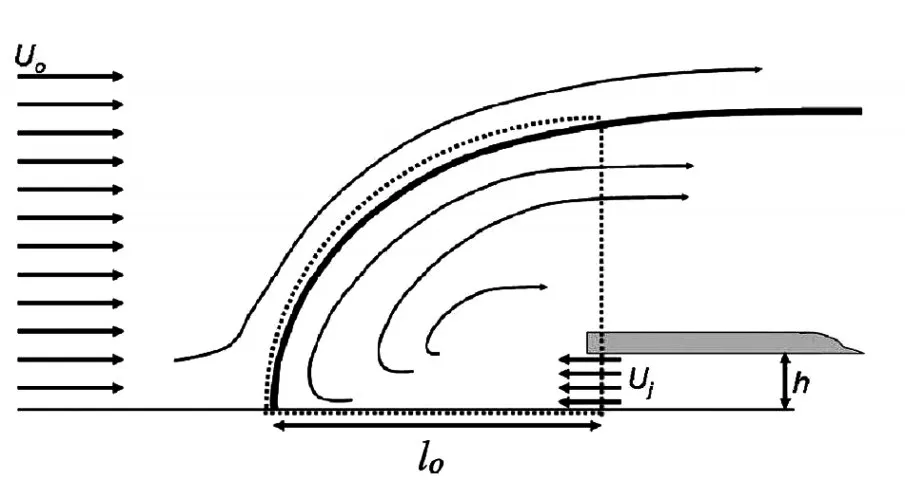
Fig.13　Stall prediction model based on zero wall shear stress[18].U0is approaching flow axial velocity,UJisthe tip reversed flow velocity,his the clearance height.Control volume is shown inside the dotted lines where axial momentum conservation applies.

Ye et al[19]recently proposed a similar model for transonic axial rotors in which the TLV reaching theLEof next blade is employed as the criterion of stall.But they include the effect of shock wave on the TLV trajectory.Again,the model is empirical and requires fitting of some coefficients.This model and one in[18]can be useful in compressor design,but they make no distinction between spike-stall and modal stall and others.They can neither explain the process into the spike-stall,nor can they predict correctly compressor stalls triggered by stators or diffusers.

3.2　Body Force Models and Eigenvalue Methods

Gong et al[20-21]put forward a body-force model to simulate the propagation of instabilities in axial compressors.This is a multi-dimensional,incompressible and inviscid flow model in the which flow turning effect of blades is replaced by a body force field.The field is continuously distributed circumferentially,and the rotor is assumed to have an infinitive number of blades to restrict the flow redistribution peripherally,as illustrated in Figure 14.

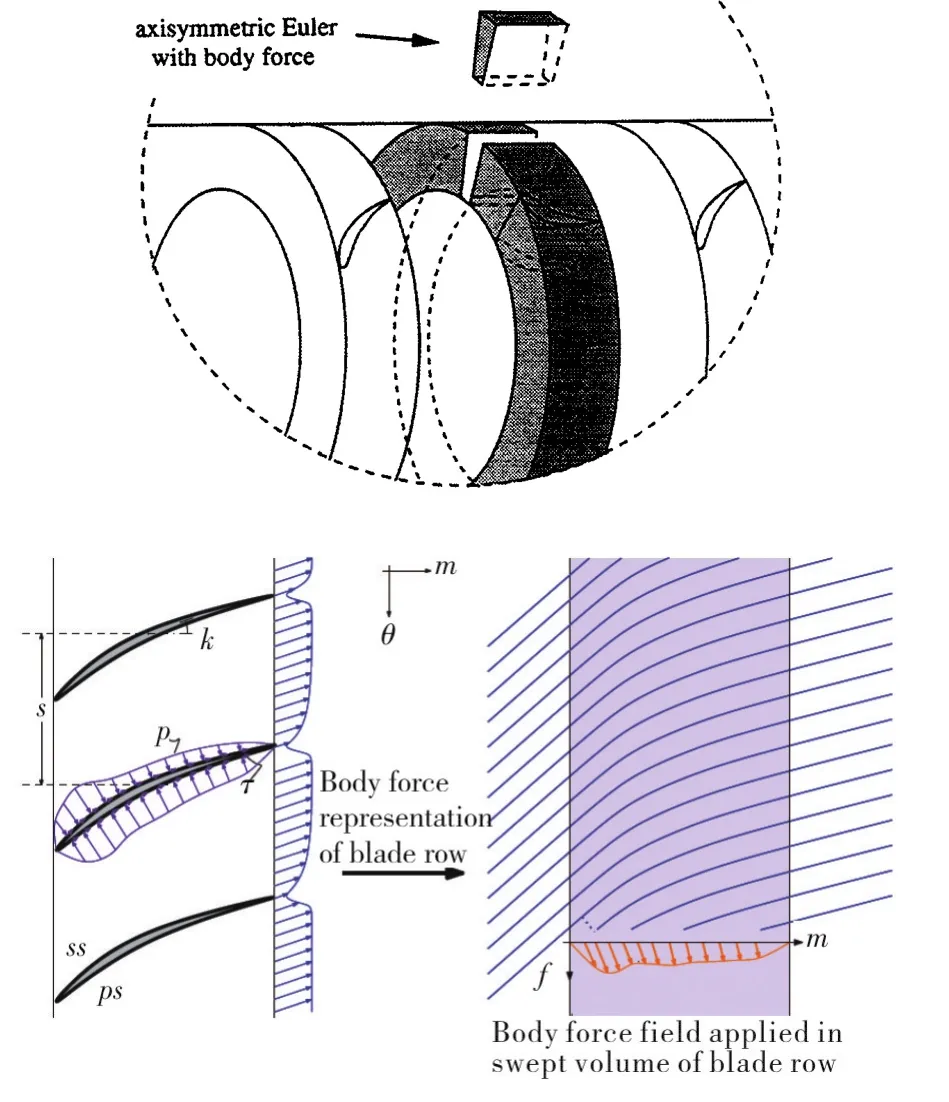
Fig.14　Body-force model for stall prediction[20-21]

By imposing an initial disturbance of modal or spike type,the model forms a group of differential equations that may be numerically solved along the time axis.The method was later extended to include viscous forces and applied to a centrifugal compressor[22].To obtain body force distribution, the steady flow Navier-Stokes equations are solved for a single blade passage at near numericalstallpoint,and theresultsareused to extrapolate or to build a model for the body force calculation.This method requires an initial disturbance while real compressors do not;and the body force calculation often diverges,reflecting the problems in force model building using the extrapolation.

To overcome the need for an initial disturbance,Sun and his co-operators[23-24]linearised the body force model,and assumed normal mode disturbances to change the problem from an initial value one to an eigen value one.The method was applied to a transonic fan and axial compressor[25-26]and latter to centrifugal compressor[27].But the transformation to an eigen value problem from an initial value problem also means that the method makes no distinction between different stall modes and the ability to track the inception process to spike-stall is lost.In addition,some arbitrary features of the body force model still exist.

Everitt and Spakovszky[28]modelled an isolated vane diffuser in a turbocharger compressor.A spike type initial disturbance has to be imposed,and the model can then be solved to show the system response.Earlier Spakovszky and Rodunes[4]solved a linearised model of centrifugal compressors for instability using normal mode and eigenvalue method.

3.3　Discussion

Experimental and numerical evidences have shown that compressor stall is a multi-scales event with at least two different time-space scales.The spike-stall has a length scale of one pitch initially and an associated short time scale;while the modal stall has a length scale of rotor periphery or a large fraction of it and a much longer time scale.Any models or theories trying to predict compressor stall must be able to handle at least these two different scales.In this regard,the eigenvalue and normal mode method are likely to fail because they are based on the concept of Lyapunov stability in which an infinite time horizon is allowed for the departure and the return to equilibrium when checking the stability of a system.An infinite time horizon does not account for the many time scales that characterise local fluid processes,such as the different time scales of spike-stall and modal stall of compressors.In fact,it can be argued that most dynamic processes in wall-bounded shear flows occur on a finite time scale,often related to,e.g.,a characteristic eddy turnover time or the lifetime of coherent structures involved in the process.So a stability definition that is based on an infinite time horizon seems to run counter to the observation of finite-time processes.

For this reason,it may be more fruitful if we abandon the concept of Lyapunov stability and adopt a new stability concept as the amplification of the initial perturbation energy over a prescribed time interval[29-31];thisdefinition reintroducesthe timevariable asa parameter.The amplification of the initial energy of course depends on the initial condition.This dependence can be eliminated by optimising over all permissible initial conditions and accepting the maximum as the optimalenergyam plification.Mathematically,wecanwrite

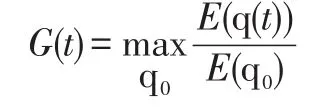
WhereG(t)is the optimum energy amplification,E(q(t))denotes the energy of the perturbationq,q0the initial perturbation,and the maximising is performed over all the permissible initial conditions.G(t)can be obtained by SVD (singular Value Decomposition).So one may examine the behaviour ofG(t)of a compression system in small time scales for spike-stall type of instability,but in much larger time scales for modal instability.

Another useful concept is the non-normality concept also developed in modern hydrodynamics[29-31].In traditional stability analysis,different modes or system eigen vectors are assumed to be orthogonal or normal to each other,hence the term normal mode,and eigenvalue analysis is applied.It is now known,however,that the eigen vectors of the flow systems governed by Navier-Stokes equations are usually non-normal.Only for a normal system,eigenvalues fully describe the system’s behaviour;for a non-normal system,eigen vectors must also be considered.Systems with non-normal eigen vectors can exhibit transient growth,even if eigen values indicate long term stability.Figure 15 illustrates this transient behaviour.

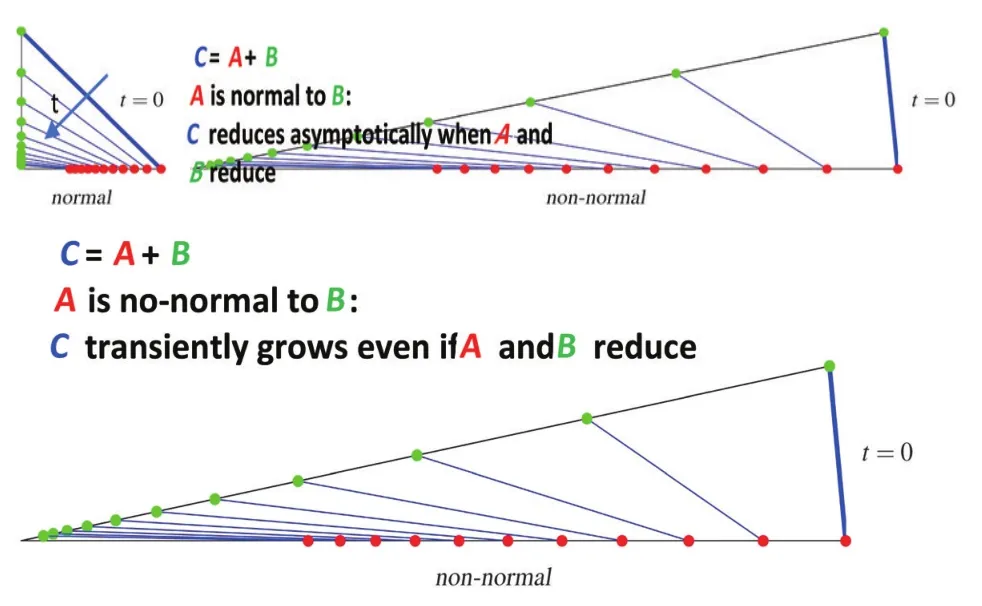
Fig.15　Geometric interpretation of transient growth

This author and his co-works[32]applied the nonormality analysis to a vaneless diffuser governed by linear Euler equations,and observed transient energy amplification as shown in Figure 16.In this work,linearised Euler equations were applied to a parallel wall vaneless diffuser,both eigen values and the optimum energy amplificationG(t)were computed.In the case shown here for the first circumferential mode with a diffuser outlet-to-inletradius ratio of 1.5 and dimensionless inlet radial velocity of 0.09,all the eigen values are negative,which indicates a Lyapunov stability.G(t)on the other hand shows that the diffuser can experience a transient energy growth.One implication of such a growth is that if it is sufficiently large,it may invalidate the linear assumption,including the Lyapunov stability conclusion that comes out the assumption.

Fig.16　Transient growth of a vaneless diffuser described by linear Euler operator[32]

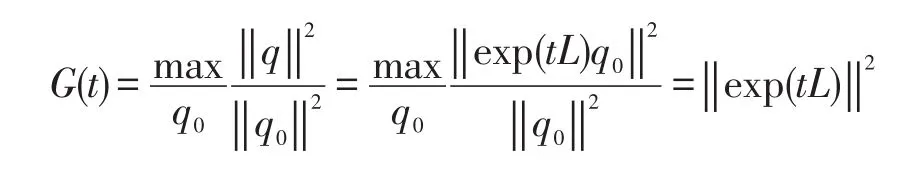
Given the unusually rapid increase of the perturbation amplitude in spike-stalls,a hypothesis may be putforward that such a swift change involves transient growth.A linearno-normality analysis is therefore relevant because the finite amplitude of the spikes must first come from small spikes,as indicated by the experimental results of axial compressors in Figures 9 and in Figure 17:

Fig.17　Measured spike-stall inception of a transonic axial compressor,showing intermittent spikes before final stall sets in[16]

4　Conclusion

This paper reviews the research work on spike-stall of compressors.It seems that decades of research has provided us with many useful information of this rapid stall phenomenon,yet we have still not fully understood its underlying flow mechanism.Prediction of its occurrence is also met with great difficulty.

Some new concepts have been proposed to overcome some of these difficulties.It is pointed out that current forecasting methods are mostly based on classic stability theory which is incapable of handling the transient growth and diminution of disturbances in multiple time-length scales that typify compressor stall.Modern transient instability concept is suggested to reestablish the link between time and the maximum amplification of the system to initial perturbations.The non-normality of compressor system is also emphasised.

5　Acknowlegements

The author thanks Dr X.C.Zhu and Mr C.X.Hu of Shanghai Jiaotong University for many fruitful discussions on transient growth and no-normality.The usefulsuggestionsandcommentsbytheunknown reviewer of CICT are gratefully acknowledged.