低雷诺数下的钉螺绕流特征数值模拟

，，，　

(1.长江水利委员会 综合管理中心，武汉　 430010；2.河海大学 水利水电学院，南京　210098；3.长江科学院 院长办公室，武汉　430010)

1　研究背景

钉螺是日本血吸虫病传播的唯一中间宿主，通常随水流迁移扩散。钉螺的在动水、静水中的起动、沉降和漂移规律是设计水利阻螺措施的主要依据。张威等[1-2]对钉螺的动水沉降规律进行了观测及研究，长江科学院等单位通过实验观察建立了钉螺的静水沉降公式[3-6]。基于上述研究，长江科学院、湖北省血吸虫病防治研究所、武汉大学等单位提出了沉螺池等有效的水利阻螺设施。通过多年的科学防控，我国钉螺分布得到有效控制，为进一步提高水利血防工程的阻螺效率，更有效地控制钉螺扩散，需对钉螺在水流中的运动规律做更精细的研究。

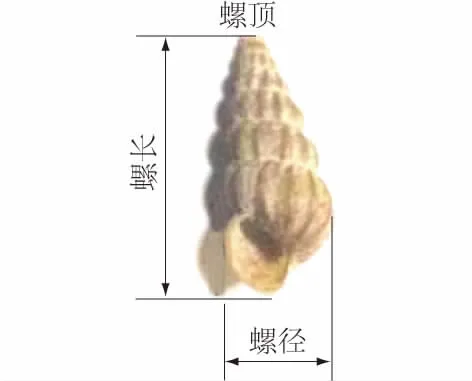
图1　肋壳钉螺

钉螺的外形对钉螺在水中的运动规律有较大的影响。如图1所示钉螺的外形近似圆锥体，代表钉螺形体的特征值主要是螺长h和螺径d。通过螺长h与螺径d的比值φ将钉螺划分为幼螺(φ<2.0)、中螺(2.0≤φ≤2.5)、大螺(φ>2.5)3级，不同级别的钉螺力学性质也有所差别[5]。根据螺壳表面纵纹的不同,钉螺分为光壳和肋壳2类，光壳钉螺与肋壳钉螺对水流阻力的影响也各有不同，分布在湖沼和水网区域钉螺一般为肋壳钉螺[6]。据观测，钉螺一般在岸边水流较缓的区域活动，钉螺在静水沉降时一般能保持平稳，螺长方向多与水流方向垂直，但在动水中漂移的姿态则复杂得多。

本文使用开源流体力学计算软件OpenFOAM对较低雷诺数肋壳钉螺在螺径与水流平行(简称“横向水流”)和螺径与水流垂直(简称“纵向水流”)2个典型条件下的绕流开展数值模拟研究，对钉螺绕流中的尾流结构、卡门涡街的形成等现象进行分析，对比2个方向上的差异，为进一步掌握钉螺扩散规律、改进水利阻螺措施提供理论依据。

2　数学模型、网格划分与数值方法

钝体绕流的数值模拟一直以来都是流体力学领域的研究热点，国内外众多学者在数值模拟方面已有深入细致的研究，但对钉螺外形这样复杂边界的钝体绕流现象的研究却十分少见。

本文运用有限体积法，利用高斯公式对二维不可压缩流体的控制方程进行离散，将控制方程转换为代数方程来求解，其中，对流扩散项、压力梯度项采用二阶精度的中心格式离散，非恒定项使用一阶精度的隐式离散，时间步长根据雷诺数的不同选取适当的时间间隔。压力与速度耦合采用PISO算法，从而在数值计算中能够比较准确地满足边界条件提高解的精度。离散得到的代数方程采用Gauss-Seidel迭代法求解。

2.1　控制方程

在笛卡尔坐标系下二维不可压缩黏性流动控制方程的无量纲形式为：

(1)

(2)

(3)

式中：u,v分别是x,y方向上的流速：Re为雷诺数;p为流体的静压强。

2.2　计算区域及模拟对象

本文选取较有代表性的肋壳中螺进行数值模拟研究。本文模拟的中螺特征值φ=2.27，螺高为h，螺径为d，其等面积圆的直径为D，计算区域为无界流动状态。为了使计算边界对数值模拟的影响最小，本文尝试使用足够大的计算区域来消除边界对计算的影响，当钉螺距来流入口边界超过20D时，上游及上下边界对流动的影响几乎可以忽略，因此本文的计算区域高达40D×40D。钉螺位于计算区域的中部，横向水流条件下螺径与x轴平行，纵向水流条件下螺径与x轴垂直。

各边界条件如下所述。①来流面(inlet)：U为均匀来流的流速，来流方向沿x轴正方向。②出流面(outlet)：指定为压力出口。③固墙(钉螺)：采用无滑动条件。④上下边界(wall)：采用无滑动条件，速度与来流面一致。

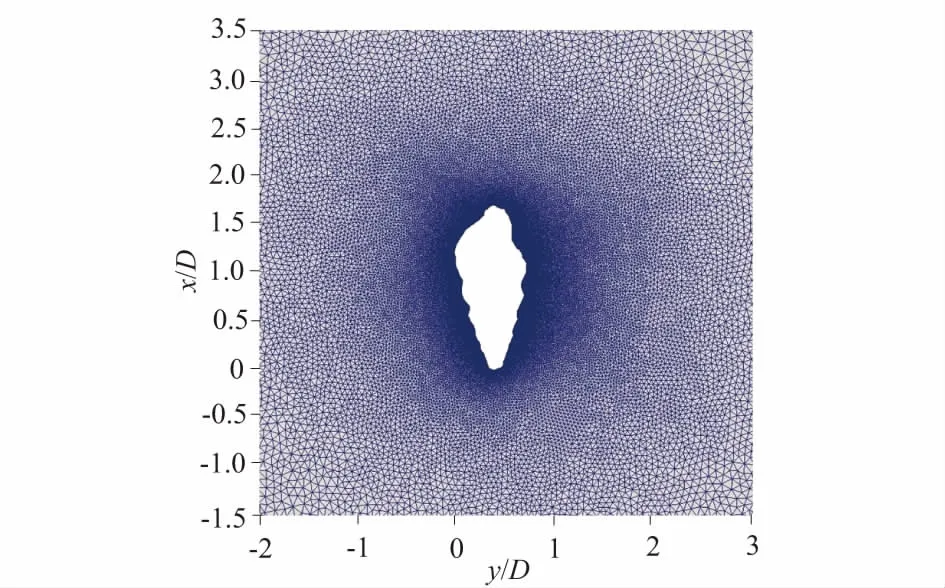
图2　钉螺附近网格划分

2.3　网格划分

如何拟合螺体的复杂边界是本研究要解决的重要问题之一。此研究使用非结构化的三角形网格贴合钉螺的复杂边界，并对钉螺表面附近的网格进行加密处理，以保证物理量变化较剧烈区域的计算精确性，如图2所示。作比对的二维圆柱体尽管具有规则的几何边界，在网格划分时有曲线网格、结构化网格等多种选择，但为保证计算结果更具可比行，在计算二维圆柱绕流时也使用相同算法划分为三角形网格。

3　计算结果分析与讨论

颗粒雷诺数Red、阻力系数CD、斯特罗哈数St等无量纲数是描述低雷诺数下钝体绕流规律的常见参数，其定义分别为：

(4)

(5)

(6)

式中：U为均匀来流的流速；D为特征长度，本文取圆的直径或钉螺等面圆直径；ν为运动黏滞系数；FD为钝体受到的阻力；ρ为流体密度；S为迎流面面积；f为漩涡脱落频率，本文通过阻力系数CD的周期变化来得到漩涡脱落的周期。

3.1　算法有效性验证

确定以二维圆柱绕流验证计算方法的准确性及有效性的理由有3点:①二维圆柱绕流计算是验证外部流求解的事实标准之一;②钉螺绕流的水流结构实验观测及数值模拟资料都较少，而二维圆柱绕流有大量的试验观测和模拟计算数据作比对;③目前在研究钉螺运动研究时多将其概化圆形或球形。

二维低速定常绕流的流型与颗粒雷诺数Red有关。Red>4时流体脱离圆柱表面，在下游形成一对固定不动的对称回流区域；Red>47时圆柱后缘上下两侧有涡周期性地轮流脱落，形成规则排列的卡门涡街；Red>180后尾流呈现出三维形态[7]。

本文首先计算Red=40，80时二维圆柱绕流与已有数值模拟数据比对以验证算法:Red=40时，随着计算进行阻力系数CD、回流区长度Lw逐渐趋于稳定；Red=80时，阻力系数、升力系数出现周期性震荡，同时下游回流区不再存在，取而代之的是涡周期性脱落而形成的卡门涡街，斯特罗哈数St为描述卡门涡街的脱落频率的无量纲数。阻力系数、回流区长度和斯特罗哈数等与Mittal等[7-10]的数值模拟结果基本一致，验证了算法的有效性。

3.2　横向水流条件模拟

本文首先模拟了钉螺处于横向水流时，在不同雷诺数(Red=1，2，3，4，10，20，30，40，50)下的流场，并对尾流的形态及变化规律作了初步分析。计算表明，钉螺绕流流动同二维圆柱绕流一样，随着雷诺数的增加，展现出2个重要的流态变化：一是雷诺数达到一定值后流体脱离螺体在下游形成稳定的附着涡;二是雷诺数进一步增大后钉螺下游附着涡瓦解形成卡门涡街。

图3(a)给出了Red=1时，钉螺周围流场的迹线图，钉螺表面流动无分离现象，流体也未脱离螺面；图3(b)为Red=10时，流体经过钉螺表面后开始脱落并形成固定不动的非对称旋涡，涡内流体自成封闭回路而形成“死水区”，尾流区长度Lw为钉螺末端到“死水区”末端的长度。

图4　Red=40时不同时刻涡量云图

Red≥30时，附着涡瓦解，流体通过钉螺后下游不再是定常流，而是周期性上下脱落形成卡门涡街。图4选取了Red=40时一个脱落周期[0，T]内3个具有代表性时刻的涡量云图(T为一个脱落周期时长)。涡脱落的周期图中清晰地表现了流场运动的周期特性，在t=0和T时刻，涡量图实际上是相同的，0时刻上部涡即将脱落，而t=T/2时刻的涡量图是t=0和T时刻的镜像，下部涡即将脱落。实际上，t=T/4与3T/4时刻也互为镜像。

本文计算钉螺的雷诺数Red、阻力系数CD、斯特罗哈数St等无量纲数时，特征长度D均取钉螺等面圆直径。从表1可知：

(1)Red≤3时，流体未从钉螺表面脱离,Lw/D=0，此雷诺数范围的绕流称为斯托克斯区。

(2)4≤Red≤20时,流体开始从钉螺表面脱落形成尾流，且随着Red的增加“回流区”长度Lw/D明显增大，此雷诺数范围的绕流称为对称尾流区。

(3)Red≥30时,尾流出现非稳定态，回流区演变为卡门涡街，描述旋涡脱落频率的斯特罗哈数St随着Red增加基本保持稳定，此雷诺数范围的绕流称为卡门涡街区。

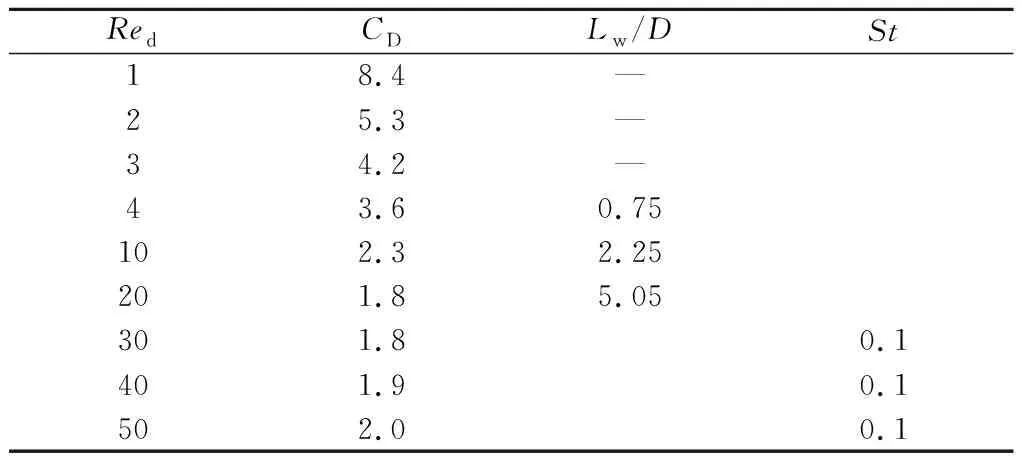
表1　横向水流不同雷诺数下钉螺阻力系数、尾流区长度和斯特罗哈数

注：Red≥30后的阻力系数CD为一个脱落周期内的算术平均值

在螺径与水流方向平行时，与等容圆柱相比，二维钉螺绕流随Red的增加呈现相同的3种尾流形态，不同之处在于：

(1)二维圆柱绕流分离点临界雷诺数Rec约为4[9]，钉螺则在3～4之间。

(2)二维圆柱绕流由对称尾流区过渡到卡门涡街区的临界雷诺数Rec约为46[9]，钉螺则在20～30之间。

(3)相同雷诺数下钉螺下游回流区长度、斯特罗哈数均小于二维圆柱绕流。

图5　 Red=40时CD-t关系

当Red≤20时，水流通过钉螺后均为恒定流，阻力系数亦为恒定值；其中，Red<3是水流通过钉螺后几乎无流动分离，阻力以摩擦力为主；4≤Red≤20时水流通过钉螺后有流动分离，钉螺后方回流形成一对驻涡，阻力由摩擦阻力和压差阻力2部分组成；当Red≥30后，流动不再保持恒定，水流在钉螺后方交替脱落形成卡门涡街，此时阻力主要由压差阻力产生，阻力随旋涡脱落的规律周期性变化。图5截取了Red=40时CD随时间变化关系图，明显看出CD随时间变化的波形图是由2个波叠加而成，该现象在其他钝体绕流现象(如：圆柱、方柱绕流)中均未出现。

3.3　纵向水流条件模拟

基于相同的算法和模型，本文模拟了钉螺处于纵向水流条件时，在不同雷诺数(Red=20，40，80，120，140，160)下的流场。计算表明，螺径平行水流方向与螺径垂直水流方向时一样，随着雷诺数的增加，同样展现出3种重要的流态变化。图6(a)给出了Red=40时钉螺周围流场的迹线图，钉螺表面流动的流体未脱离螺面；图6(b)为Red=80时，流体经过钉螺表面后开始脱落并形成固定不动的非对称旋涡，涡内流体自成封闭回路而形成“死水区”。

图6　纵向水流条件下钉螺绕流迹线图

2种流向下的差异也十分明显，从表2可以看出：

(1)纵向水流条件下，得到2个临界雷诺数Rec分别在区间(40，80)和区间(120，140)范围内，远大于横向水流条件下的临界值。

(2)处于第2种形态(对称尾流区)时，随着雷诺数的增加尾流区长度并无明显增长。

(3)在第3种尾流形态(卡门涡街区)，涡的脱落频率也基本保持稳定，但纵向水流条件下涡的脱落频率远大于横向水流条件下的频率。

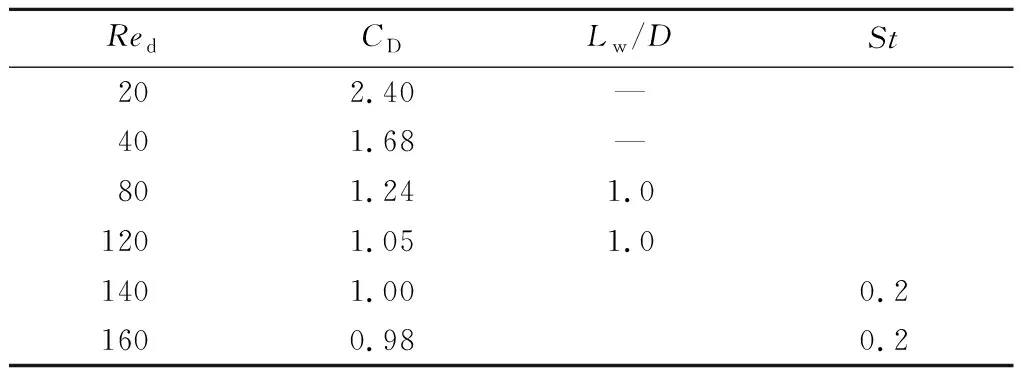
表2　纵向水流不同雷诺数下钉螺阻力系数、尾流区长度和斯特罗哈数

注：Red≥140后的阻力系数CD为一个脱落周期内的算术平均值

不同流向下Red-CD关系对比如图7所示。从图7看出，2种流向下阻力系数总体上随Red的增加而减小，但自流体从钉螺表面开始脱落后，阻力系数CD减小的速度明显变缓，且卡门涡街区的CD变化规律同横向水流条件下一样，也是由2个波形叠加而成。Red=20时，纵向水流条件下绕流尚处于斯托克斯区，但横向水流条件下绕流已处于卡门涡街区。尽管此时纵向水流条件下阻力系数>横向水流条件的阻力系数，随着Red的增加，纵向水流条件下的阻力系数迅速下降，Red>35.2后阻力系数反而低于横向水流条件下的阻力系数。这一反常现象说明钉螺绕流在卡门涡街区比较特殊，阻力系数的算术平均值并不能正确反映水流对钉螺的阻力作用。

图7　不同流向下Red-CD关系对比

4　结论与展望

4.1　结　论

通过对低雷诺数下的横向和纵向2个流向下钉螺绕流的直接数值模拟(DNS)可知，同其他钝体绕流现象一样，钉螺绕流在不同的雷诺数下呈现出3种不同的尾流形态，不同在于：

(1)3种尾流形态转变的临界雷诺数Rec有差别，钉螺横向水流<圆柱<钉螺纵向水流。

(2)钉螺在横向水流条件下，下游回流区长度随雷诺数的增加明显，但在纵向水流条件几乎不随雷诺数变化。

(3)阻力系数CD随雷诺数增加而减小。

综上所述，钉螺绕流和其他钝体绕流现象相比，有共性也有不同。钉螺外形复杂有其独特的水动力学特性，在进行钉螺的水力学研究时不能简单概化为简单的几何体。

4.2　展　望

今后还需开展以下方面的研究：

(1)提高钉螺数值模拟的精度，进一步提高钉螺模拟效果。

(2)开展钉螺绕流试验观测研究以更有效地验证数值模拟结果，进一步丰富对钉螺随水流扩散规律的认识。

(3)钉螺在卡门涡街区CD的变化规律较为特殊，需进一步深入研究。