一道力学题的多种解法

李开玮

(广东理工学院工业自动化系　广东 肇庆　526100)

1　问题描述

如图1所示，A,B两物体由一长为l的刚性细杠相连，A,B可在光滑轨道上滑行．若A以恒定速率v向左滑行．当α=60°时，物体B的速度为多少？

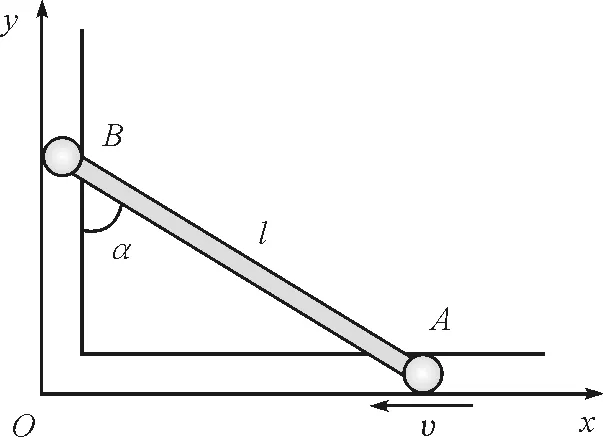
图1　力学题图及坐标系

2　问题解答

(1)质点运动方程解法

如图1所示，建立直角坐标系，设A的坐标为(x，0)，B(0，y)，物体A的速度为

细杆长度为l，有

x2+y2=l2

两边对时间求导有

(2)运动的合成与分解

对A，B来说，运动可以沿杆方向和垂直杆方向作分解，如图2所示由于细杆是刚性的，故有A，B沿杆方向的分速度相等

vAsinα=vBcosα

因此

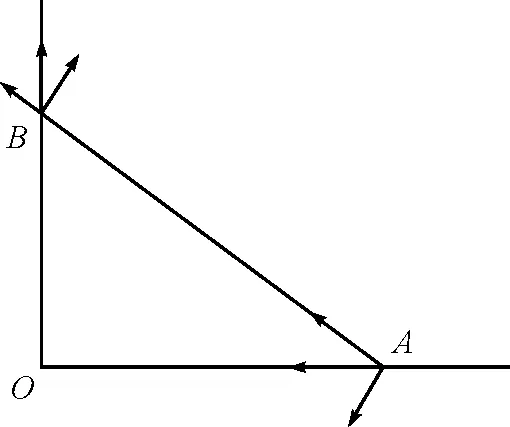
图2　速度的分解

(3)刚体的瞬心

对于任一作平面平行运动的刚体(或它的延伸体)，在任何瞬时，其上总有一点O′，其速度vO′=0，这时整个刚体只能围绕此点旋转，这个点叫做刚体的瞬时转动中心或瞬心[1]．例如在平面上做纯滚动的圆柱体或球体，与平面的接触点就是它的瞬心．

对于细杆来说，如图3所示.

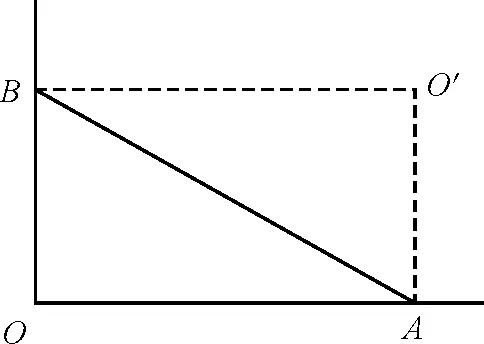
图3　细杆运动的瞬心

其运动瞬心为A，B运动方向的垂线的交点O′．设细杆绕瞬心瞬时角速度为ω，则有

ω·O′A=vA

ω·O′B=vB

故有

3　结语

通过上文的讲述，对于两连接体的问题，要仔细观察两物体的联系点，将两物体的速度联系在一起，才好根据其中一个物体的已知速度求出另一个物体的未知速度，上面三种方法基本涵盖了解决这类问题的所有方法，值得学生好好体会，举一反三．