探究物体在线性力作用下的运动形式

郑 金

(凌源市职教中心　辽宁 朝阳　122500)

瞬态变量的初始值f(0)=x0、稳态值f(∞)=x∞和时间常数τ是瞬态过程的三要素，解答这类问题关键是应用物理规律推导出某个变量的微分方程的标准形式，再利用瞬态过程的三要素写出微分方程的通解即瞬态过程的物理量随时间变化的表达式.下面以物体在线性力作用下的直线运动问题为例进行分析.

1　物体只受线性力的作用

这表明，速度变化量跟位移成正比，即速度随位移均匀变化，把这种运动称为另类匀变速运动.

如果物体受到的线性力为动力，那么速度随时间如何变化呢？下面推导关系式.

设速度v=v0+Ax，则加速度

由牛顿第二定律有

由此得微分方程的标准形式

图1

可得x=x0eAt.当t=0时x=x0，不为零.这表明当t=0时物体已经发生了位移，因此运动物体的计时起点与位移起点不重合.如果选择运动物体的计时起点与位移起点重合，那么v≠Ax，即不存在速度跟位移成正比的运动，这是因为v=v0eAt中的初速度v0不能为零，则v=v0+Ax中的v0不能为零，所以v≠Ax.虽然由v=Ax在数学上也可推出v=v0eAt，但不合实际.

图2

只要物体受到的作用力跟速度成正比，而且是阻力，做减速运动，就是瞬态过程，因此速度随时间变化的图像存在水平渐近线.对于这种瞬态过程，速度随位移均匀变化，而不是成正比.

【例1】如图3所示，光滑U型导轨PQMN固定在水平面上，处于竖直向下的匀强磁场中，磁感应强度为B，导轨宽度为L，QM之间接有电阻为R，其余部分电阻不计.一质量为m，电阻也为R的金属棒ab垂直放在导轨上，给棒一个水平向右的初速度v0使之开始滑行，最后停在导轨上，对此过程，求：

(1)在电阻R上产生的焦耳热；

(2)通过电阻R的电荷量和ab棒运动的位移；

(3)位移随时间变化的关系式.

图3　例1题图

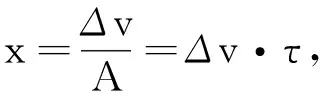
2　物体受恒力与线性阻力共同作用

如果物体同时受到恒力与线性阻力的作用而做直线运动，则运动过程为瞬态过程.物体受到的合力与速度关系是一次函数关系，从数学角度而言，仍然属于线性关系.

【例2】在无风的情况下，一个质量为m的雨滴由初速度v0开始在竖直方向自由下落.受到空气的阻力与速度的一次方成正比，即f=kv，求其运动过程的速度、加速度和位移随时间变化的规律是什么？(雨滴在运动过程中的质量变化忽略不计)

解析:雨滴所受重力为恒力F=mg，受空气阻力为f=kv，由牛顿第二定律列出关于速度的一阶线性微分方程为

变形为

取导数可得加速度为

速度图像如图4(a)所示，加速度图像如图4(b)所示，都存在水平渐近线，这种加速运动过程是瞬态过程.

图4

由此可得位移随时间变化的关系式为

考虑到图2(a)中的凹边梯形与图4(a)中的凹边梯形相似，那么对于图4(a)，速度图线与时间轴围成的凸边梯形面积等于对应的矩形面积S1=v∞t与凹边梯形面积S2=Δv·τ之差.其中

只要物体受到线性阻力f=kv的作用做减速运动，或者物体在恒力F和线性阻力f共同作用下做减速直线运动或加速直线运动，物体将趋于停止或趋于匀速运动，有关物理量随时间变化的过程是瞬态过程.