战术激光武器跟瞄精度分析

易 瑔，孙先知，杨建昌，王林森，何炳阳

（陆军装甲兵学院，北京 10072）

0 引言

激光武器作为一种新型的定向武器装备，通过对目标的捕获、跟踪、瞄准，来实现精确打击。激光武器与传统的武器装备相比，具有反应速度快，方向性好，能够实现即发即中的优点［1］。但是这也意味着激光武器不仅需要高功率或高能量的激光器，还需具有精密的跟踪瞄准系统［2］。跟踪瞄准系统的误差会造成激光光斑在目标处能量密度的急剧下降，影响激光武器的毁伤效果，所以必须提高跟瞄系统精度，使激光光斑锁定在目标的某一固定部位，并持续数秒［3-4］。本文理论计算了激光远场发散角，分析了影响激光武器命中概率和光斑稳定概率的因素，确定了在不同大气环境下，激光武器对跟瞄精度的要求，并对跟瞄精度的误差源进行了分析，提出了有效的抑制方法。

1 激光的远场发散角

引起激光远场发散角发散的主要因素有，衍射效应、大气湍流和热晕。但对高能激光武器来讲，一旦热晕等非线性效应发生，高能激光武器的杀伤能力会急剧下降，甚至完全丧失。因此，高能激光武器的应用，必须针对实际使用环境，选择合适的激光工作波长等参数，避免热晕等非线性效应的发生。有鉴于此，这里可不考虑热晕等非线性效应而只考虑衍射和大气湍流等线性效应的影响。假设由衍射效应和大气湍流效应引起的远场发散角分别为θs、θt，则有

1.1 衍射效应对发散角的影响

光束在传播过程中，当光束横截面受到限制时，光束的传播特性会发生改变，主要表现为光能会发生重新分布，导致光束的角发散量增加，这种现象称为光的衍射效应。理想状况下，激光的发散角为衍射极限角，即

其中，β 为衍射影响因子［2］。

1.2 大气湍流对发散角的影响

大气的湍流效应是由大气的随机运动造成的大气折射率的改变引起的，激光在大气中传输时会发生光斑漂移、扩散等现象。本文主要是针对激光的扩散效应进行研究。大气折射率分布满足Kolmogorov提出的大气折射率结构函数Dn（r）的“2/3”定律：

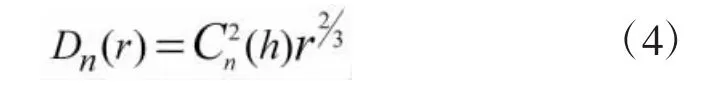
式中，r表示激光发射点与目标之间的距离，Cn为大气折射率常数［5］。一般来说按照Cn的大小，划定大气湍流的强弱［4］：

强湍流Cn＞10-6

中等湍流Cn=10-7

弱湍流 Cn＜10-8

高能激光武器射出的光束在大气中传输时，因湍流效应引起的光束角发散为：

其中l为激光传输距离，ξ（l）的表达式为

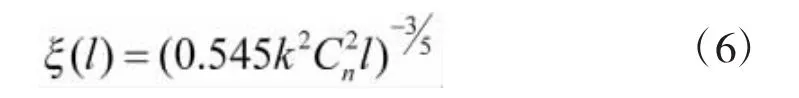
将式（6）带入式（5）得，

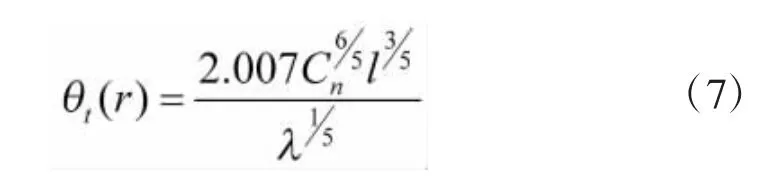
将式（3）、式（7）带入式（2）得，

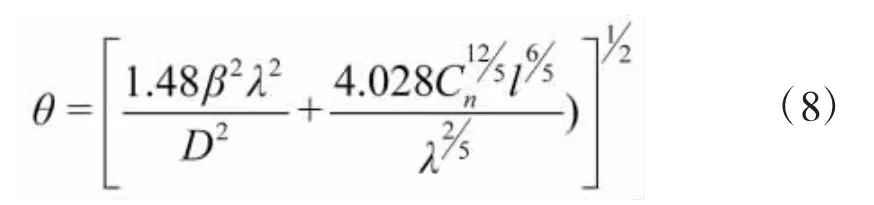
式（8）即为激光的远场发散角。

2 激光武器跟瞄精度要求

激光武器的打击方式是以一定的能量密度的激光光斑持续、稳定的照射目标瞄准点，但是由于跟瞄误差的存在，激光武器系统的跟踪瞄准精度不可能达到零误差，但显然跟踪瞄准误差又不能太大，否则引起的功率损耗相对严重，目标瞄准点区域光照功率密度会严重减小，影响杀伤效果，因此，激光武器需要尽可能地提高跟瞄精度。研究激光武器跟瞄系统的精度需求时，不仅要考虑命中概率，还要考虑激光光斑稳定概率方面的因素［6］。

2.1 命中概率

对于射击命中的判断通常有两种方法，一种是碰撞检测，即根据弹着点（激光武器的实际打击位置）与目标的偏差进行判断。第二种是根据跟瞄系统的精度，采取随机模拟的方法，确定弹着点［7-8］。虽然第一种方法更加贴近具体的实战，但是可操作性不强，具体实验实施困难，本文采取随机模拟、概率统计的方法来实现激光武器命中概率的判断。

跟踪瞄准的目的是实现激光武器对目标的精确打击，由于激光武器有别于传统武器的毁伤机制，这就需要更高的命中概率。设跟踪精度为Δθ，瞄准精度为mp。其中，Δθ以随机误差为主，可用正态分布表示；而mp为瞄准点的误差平均值。令σ为跟踪误差的均方根值，偏离瞄准点的误差Δθ总是服从正态分布，其概率密度可表示为：

概率为：

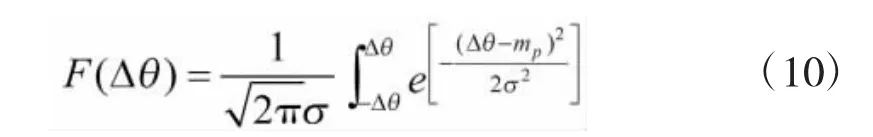
由正态分布可知：

当激光束的远场发散角θz为跟踪误差的3倍时（θz=3σ），瞄准误差 mp=0，则激光落在瞄准点的概率为99.74%；若mp=σ，则激光落在瞄准点的概率为95.44%。

当激光束的远场发散角θz为跟踪误差的2倍时，瞄准误差mp=σ，激光击中瞄准点的概率只有68.26%。在战场环境下，假设要求激光武器的精度达到 90%以上，这时 1.64＜θz＜3σ［6］。

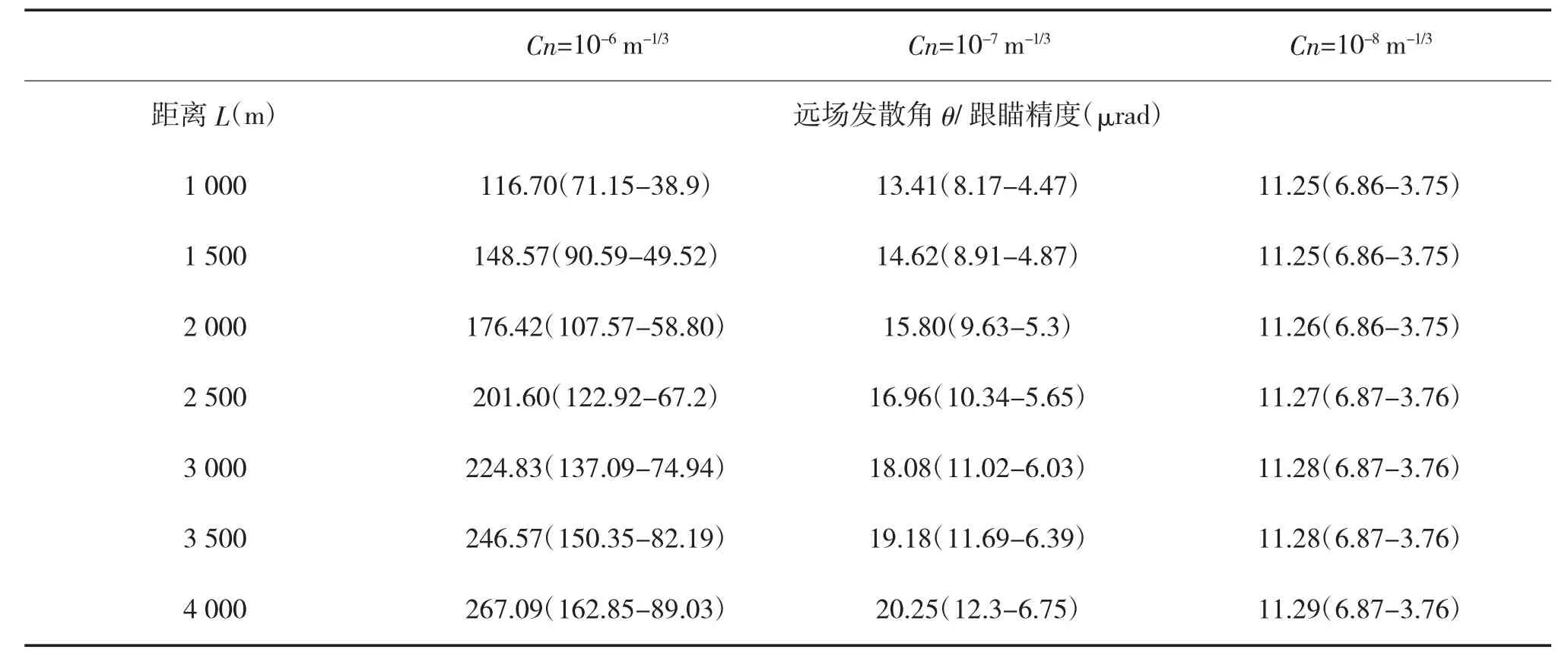
表1 不同湍流条件、传输距离时激光远场发散角θ

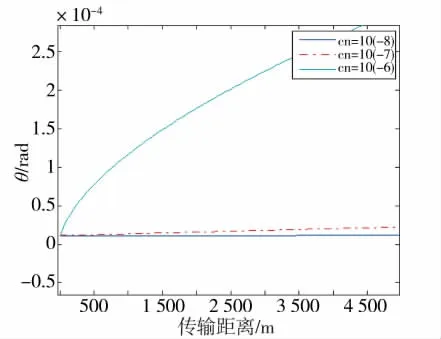
图1 不同湍流条件、传输距离时激光远场发散角θ

由表1、图1可以看出：

1）随着传输距离的增加，激光的远场发散角逐渐增加。

2）大气湍流强度越大，距离对激光远场发散角的影响也越大。

3）不同的传输距离以及大气环境对武器跟踪精度的要求也是不同的。

2.2 光斑稳定概率

假设激光武器与打击目标之间的距离为l，激光束经过衍射以及大气湍流的影响之后，在目标上的光斑直径为：

将式（10）带入式（11）得，

光斑在瞄准点抖动距离为1个光斑、1/2光斑和1/4光斑（相对远场光斑直径D），所对应的光斑质心偏移距离为D、1/2D、1/4D。假设瞄准误差是对称分布的，且满足

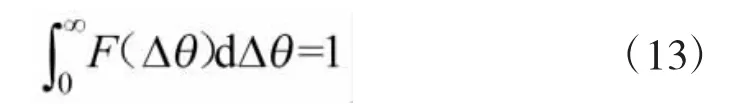
则可以认为式（13）的径向概率分布服从瑞利分布，即

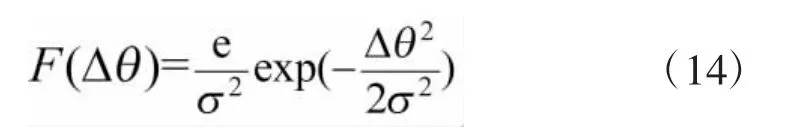
设精度要求为Δθ，则跟踪误差的均方根值σ=θ0l［6］。由此可以推断出激光武器成功瞄准的概率P为：

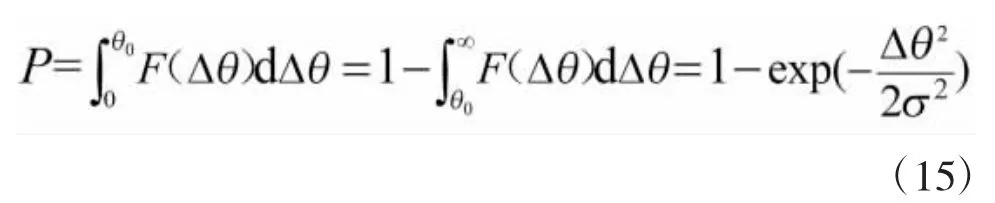
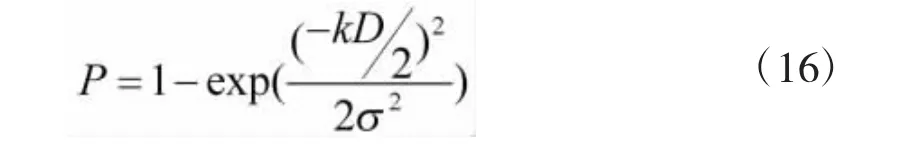
将式（12）和 σ=θ0l带入式（16）得，

2.2.1 光斑抖动量和跟瞄精度对稳定概率的影响

假设大气折射率结构常数Cn=10-6m-1/3，激光波长=1.54 μm，光束质量β=3，激光器的发射口径D=0.5 m，激光武器距离目标的距离距离l=3 000 m。根据式（16），利用Matlab得到了稳定概率与光斑抖动量、跟瞄精度的关系，如图2所示。

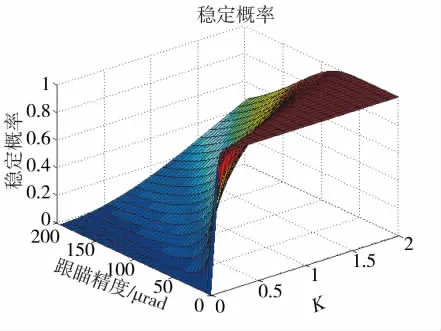
图2 光斑抖动量和跟瞄精度对稳定概率的影响

由图2可以看出：

1）随着目标点光斑抖动量的变化越来越小，在同一跟瞄精度下，光斑的稳定概率呈现出下降的趋势。

2）瞄准点的抖动量相同时，跟瞄精度越小，光斑的稳定概率越高。

为了实现激光武器的精确打击，光斑的稳定概率一般要求大于90%。若要保证光斑的抖动不超过1/4个光斑，则跟瞄精度θ≤26 μrad；若要保证光斑的抖动不超过1/2个光斑，则跟瞄精度θ≤50 μrad；若要保证光斑抖动不超过1个光斑，则跟瞄精度θ≤100 μrad。

2.2.2 传输距离和跟瞄精度对光斑稳定概率的影响

假设大气折射率结构常数Cn=10-6m-1/3，激光波长=1.54 μm，光束质量β=3，激光器的发射口径D=0.5 m，光斑抖动量不超过一个光斑，即k=2。传输距离和跟瞄精度与光斑稳定概率的关系如图3所示。

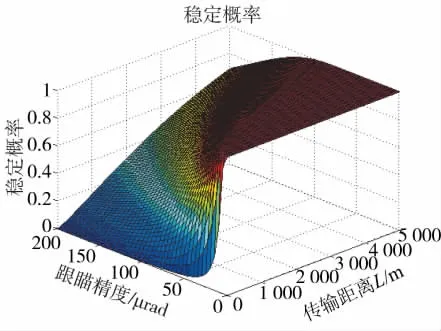
图3 传输距离和跟瞄精度对光斑稳定概率的影响

由图3可以看出：

1）当跟瞄精度≤20 μrad时，光斑的稳定概率P≥90%，传输距离对于稳定概率的影响可以忽略不计。

2）当传输的距离相同时，随着跟瞄精度的增加，光斑的稳定概率逐渐下降。

为了实现光斑的稳定概率P≥90%，瞄准目标在1 000 m时，要求光斑的跟瞄精度≤55 μrad；瞄准目标在2 000 m时，要求光斑的跟瞄精度≤80 μrad；瞄准目标在3 000 m时，要求光斑的跟瞄精度≤110 μrad；

由命中概率和光斑稳定概率来看，在不同的大气环境以及战术激光武器类型下，激光武器对于跟瞄精度的要求是不同的。我国的RCG441跟踪系统采用双探测器型复合轴结构控制，其跟踪精度达到了 20″（100 μrad）左右［5，7-8］，基本上符合不同状况下战术激光武器的使用。

3 实例分析

本文以美国海军“海石”计划中的激光武器为研究对象进行分析论证。“海石”激光武器系统中，波长=3.8 μm，激光光束出射口径D=1.8 m，光束质量因子β=3，取大气折射率结构常数Cn=10-15/2m-1/3，激光武器距离目标的距离为L=3 000 m［3］。

根据式（10），将“海石”激光武器系统的参数带入，得到激光的远场发散角为8.25 μrad。为了实现激光武器的命中概率达到90%以上，跟瞄精度要求为 σ1=5.03 μrad。

根据式（16），光斑在目标点抖动不超过1个光斑大小，光斑稳定概率达到90%以上，这时跟瞄精度的要求为 σ2=1.87 μrad。

为了实现激光武器的命中概率达到90%，同时光的稳定精度达到 90%以上，比较 σ1、σ2，要求“海石”激光武器的跟瞄精度为σ=1.87 μrad。

4 跟瞄系统的主要误差分析

影响激光武器跟瞄系统的误差源主要有传感器误差、力矩干扰误差、载体扰动误差、动态滞后误差等［6］。

1）传感器误差。传感器误差主要指的是光电跟踪传感器误差，光电传感器包括探测器件、光学系统以及信号处理3个部分。由于光电探测器的分辨率、光学系统的口径、畸变、以及信号处理的信号延迟等因素都会引起跟瞄系统的误差。为了减少传感器误差可以采用高精度的光电探测器，优化信号处理等，同时考虑对传感器误差进行补偿。

2）力矩干扰误差。力矩误差主要是由摩擦力矩、电机力矩波动和其他的干扰力矩等产生。目前，主要有以下两种方法可以减少力矩干扰误差：一是优化结构设计、减少传动环节；二是采用补偿的方法，实现力矩干扰误差补偿。

3）载体扰动误差。激光武器的跟瞄系统不可避免地受到载体平台（装甲车辆、直升机、舰艇）运动的影响，尤其在恶劣的条件下，载体平台的运动会直接因影响跟瞄精度。为了抑制载体平台的运动带来的跟踪误差，必须减少进入跟踪环节的震动和增加跟瞄系统的振动抑制能力。

4）动态滞后误差。在激光武器跟瞄系统跟踪运动目标时，由于跟瞄系统的响应速度有限，激光光束将滞后于所跟踪的目标，这就是动态滞后误差。将动态滞后误差定义为ΔθD，则有

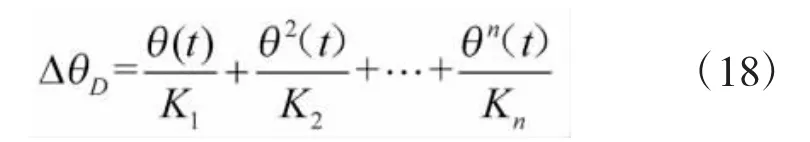
其中θn（t）为角位移的n阶导数；Kn为n阶导数误差系数，θn（t）、Kn由控制系统的传递函数决定。为了减小动态滞后误差，一般采用高型别系统（增加纯积分环节）或提高开环增益（增加Kn的值）。

跟瞄误差又可以分为动态误差和静态误差。动态误差主要包括动态滞后误差、力矩干扰误差、视轴稳定误差；静态误差主要包括机械传动误差、电器器件误差、传感器误差。根据系统设计的误差分配原则，动态误差约为静态误差的3倍～4倍。假设跟瞄系统的误差为100 μrad，按照动态误差Δθcd为静态误差Δθcj的4倍进行分配，即

跟瞄系统的总误差为

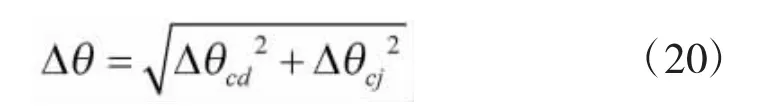
根据式（19）、式（20），得到动态误差 Δθcd=95.08 μrad，静态误差 Δθcj=4.92 μrad。静态误差中，传感器误差影响最大，占总静态误差的1/2，机械传动误差、电气部分误差各占1/4；动态误差中，对跟瞄系统精度影响程度依次为动态滞后误差、视轴稳定误差、力矩干扰误差［6-10］。

5 结论

本文通过理论计算激光的远场发散角来确定战术激光武器的命中概率以及光斑稳定概率，从而对激光武器的跟瞄精度提出了要求。针对不同大气环境和激光武器进行分析，从命中概率和稳定概率考虑，提出了战术激光武器跟瞄精度的技术指标。以“海石”激光武器系统为例进行了分析，根据现有的参数指标，提出了“海石”激光武器系统的跟瞄精度指标。概括了影响跟瞄系统精度的主要因素并提出了有效的抑制方法。

本文从激光武器系统的命中概率和光斑稳定概率方面考虑，对跟瞄精度指标提出了要求，为激光武器的设计提供了技术指标。