装甲装备保障测试设备的优化配置模型

张 雷，查晨东，常天庆，梁德潜

（陆军装甲兵学院，北京 100072）

0 引言

装备保障是装备战斗力形成的决定性因素，其费用超过全寿命周期费用的2/3，装备维修保障资源优化问题一直备受关注，并持续向节约化、精细化的方向发展。装备维修保障资源的优化问题、调度问题以及仿真验证等方面均已涌现出大量研究成果，很好地解决了许多现实问题，但多集中于对整体资源、人力资源或资源调度的优化研究，对于保障测试设备的优化配置问题研究较少［1-2］。随大量新技术在装备中的广泛应用，传统的装甲装备维修保障方式发生了深刻变革，保障测试设备逐步成为装备维修保障任务的核心手段和决定性技术力量，并占据大量维修保障费用。随之而来，迫切需要从系统角度突破相关关键技术，使测试设备资源的经济和保障综合效益最大，即在满足维修保障质量要求的前提下，尽可能提高保障测试设备的工作效率，降低测试设备配置成本。

对于装甲机械化部队，军内的维修级别主要分为基层级和中继级，二者之间的维修保障任务具有较大差异。基层级维修保障任务主要是定期保养、故障定位、换件修理以及修复少量简易部件，另还承担战时抢修任务，配属设备以便携式小修设备为主。中继级维修保障任务主要是装备各组成部件的中修、集中项修，同时负责对基层级维修的支援，配属设备以固定式、半机动式为主，能够形成较强的集中、细化维修能力［3-7］。因此，很难用一套测试设备配置方法同时去满足两个层次的维修能力建设要求，需要有针对性地开展研究。

1 基层级测试设备配置模型

基层级部队的各类装备主要用于战备、日常训练和综合性演习。在日常训练中，动用的装备数量与种类较少、修理任务不多，装备损坏原因主要来自偶然故障和耗损性故障，对保障时间的时效性要求不高，进而对测试设备的配置种类、数量要求远小于参加大型演习和战时伴随保障的要求［8-11］。因此，对于基层级作战部队，大型演习和战时抢修任务对保障测试设备的需求是决定设备配置方案的核心因素，又考虑测试设备战备储备等因素，提出以装备平均维修时间最短为目标建立设备配置优化模型，并根据部队的战备级别适度调控。

1.1 模型基本说明

假设所有故障模式都必须得到维修，每种模式有换件维修和应急维修两种方法，且每种维修方法所需的设备种类和数量已知。为此，基层级保障测试设备可划分为故障定位和维修调校两个种类，分别支撑快速换件维修和应急维修。例如，在瞄准镜破碎故障模型下，需要换件和应急两种维修方法，换件维修时需要1台观瞄系统检测仪进行故障定位，确认野战级可更换单元；应急维修时，需要1台观瞄系统原位调校设备，完成换件修理后的观瞄系统性能调校，回复作战能力。

装备故障数量由每种故障模式装备受损的概率和参战装备数量决定。针对装甲装备各部分之间相对功能独立的特点，装备子系统故障数量由下式计算可得：

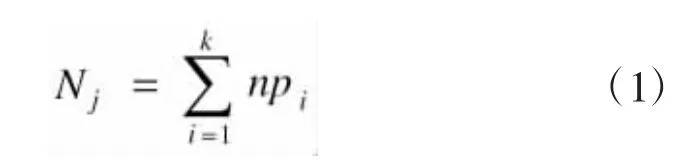
式中，Nj为装备子系统故障数量，j=1，2，…5分别指代装备功能独立的各子系统，其中j=1代表火控系统，j=2代表通信指控系统，j=3代表电气系统，j=4代表火力系统，j=5代表底盘系统；k为影响装备各子系统基本功能的故障模式数；pi为装备子系统第i种故障模式的损坏概率；n为装备数量。

则装备系统总的故障模式数量为：

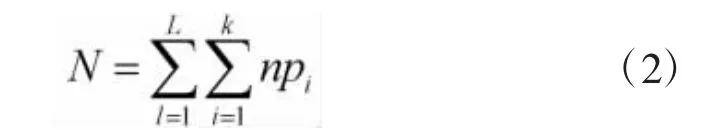
其中，L表示装备系统所包含的子系统个数。

每种故障模式有换件维修和应急维修两种维修方法，假设第i种故障模式两种维修方法的次数分别为αi1和αi2，则换件维修的比率为：

式中，xi表示第i种故障模式需要换件维修的比率；xi=1表示第 i种故障模式只需换件维修；xi=0表示第i种故障模式只需应急维修。

1.2 模型建立

1.2.1 目标函数

平均维修时间为：

其中，Ti1为第i种故障模式使用故障定位设备的平均维修时间；Ti2为第i种故障模式使用维修调校设备的平均维修时间。

1.2.2 经费约束条件

设备经费为受损装备在所有故障模式下两种处理方法所需设备的经费之和。

设备经费为：

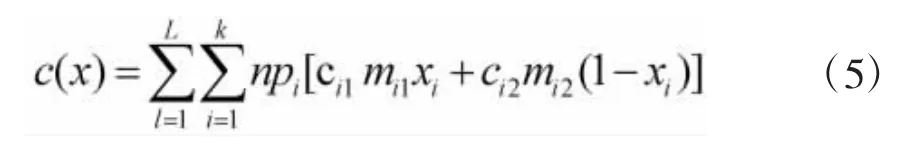
其中，mi1为第i种故障模式采取换件维修所需的故障定位设备数量，每台设备购置平均费用为ci1；mi2为第i种故障模式采取应急维修所需的维修调校设备数量，每台设备购置平均费用为ci2。

1.2.3 配置模型

即以平均维修时间最短为目标函数的设备优化配置模型为：

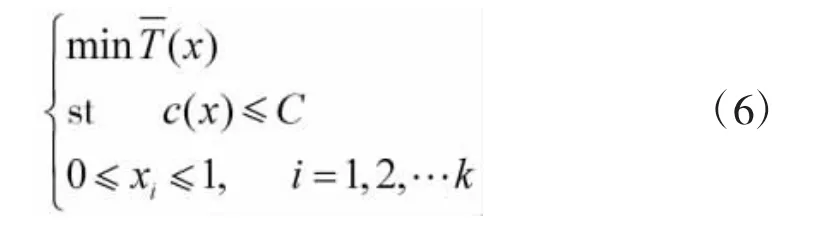
式中，C为基层作战部队保障测试设备经费限额。

2 中继级测试设备配置模型

中继级维修机构通常主要配置固定式、半机动式大型检测与维修设备，具备整车中修、高新部件集中项修、巡修等能力。在以往设备配置过程中，没有注重维修保障能力建设和设备使用效能，致使维修保障测试设备短缺与冗余现象共存。为此，提出根据区域规划目标和现状约束条件，建立线性混合整数规划模型，确定测试设备的优化配置位置和数量问题。

2.1 区域性设备能力最大覆盖模型

对新建设的中继级修理机构，设备数量为不确定，假设无需考虑原有设备影响，可使用最大覆盖模型进行配置，模型的数学表示如下：

目标函数为：

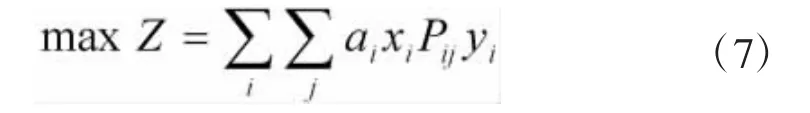
约束条件为：

进而，式（7）表示覆盖子区域内修理装备的数量最大；

式（8）保证配置设备的修理机构能够覆盖子区域i；

式（9）表示设备的采购成本限制，通过连续变动其取值，可以得出要覆盖所有子区域的保障测试设备最小数；

式（10）表示 xi和 yi是 0，1 变量。

模型中各个参数表达如下：i为子区域的下标；j为申请配置设备的中继级修理机构下标；I为子区域集合；J为申请配置设备的中继级修理机构集合；ai表示子区域i每年需要使用测试设备次数；；Pij表示子区域i到中继级修理机构j的送修的概率；；dij表示子区域i到中继级修理机构j的最短距离；P表示保障测试设备的采购价格；B为年度保障测试设备采购预算；S表示设备能够覆盖的最大距离；Ni表示所有能覆盖子区域i的中继级修理机构的集合，所有

2.2 区域性设备建设时序规划模型

在满足上述设备最大覆盖配置模型的基础上，基于工程应用实际，提出如下配置时序规划模型。

受保障经费、测试设备供需情况、维修保障任务量变化等因素的影响，测试设备的配置不可能在建设期的第一年就全部到位，需要分阶段、分步骤地实施，从而避免部分设备闲置，出现设备等装备的问题。模型假设将设备建设期按年度分为不同的建设阶段，建设阶段的集合为表示将建设期分为r个建设阶段；并假设建设期内提出申请的共J家修理机构

2.2.1 目标函数

模型以建设期内装备维修的可达性和效率的总和作为模型的目标函数。

1）维修任务可达性目标

中继级修理机构的建立数量有限，中修检测设备价格昂贵，最大化使用效益是完成优化配置的核心要素。因此，模型将区域装备送修的总距离最小化为规划目标之一，即：

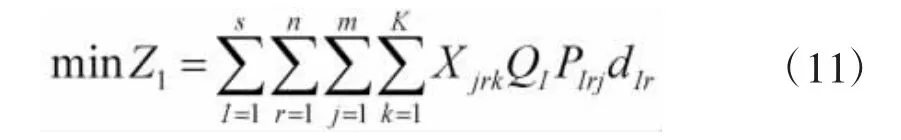
其中，QI为区域I总装备数量；PIrj为区域I的装备第r年到修理机构j送修的概率；dIj为区域I中心到修理机构j的距离。

2）设备使用效率目标

在区域测试设备的优化建设中，设备配置到合理的区域才能发挥应有的最大效能，因此，设备使用效率的最大化应为一个重要优化目标。设备的年平均使用率是一个衡量设备可靠性、测试能力和使用频率的综合指标，可以切实地衡量设备的使用效率，进而选择以设备年平均利用率作为具体的优化指标，即：

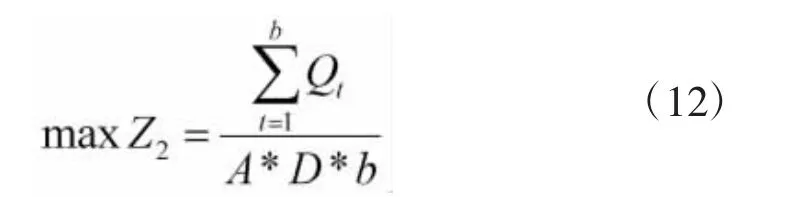
其中，Qt表示第t台设备的年使用次数；A表示设备的日最大工作时间；D表示设备平均年工作天数；b表示设备的总台数。

2.2.2 约束条件

1）资金预算约束

在整个建设期内，测试设备建设的保障费用有上限约束，即：

式中，Sk为k型设备单价，A为在整个建设周期内保障费用的预算上限。

2）设备必须配置约束

随着装甲装备种类和数量的变化，部分维修机构的装备修理任务种类和数量增多，而按时完成修理任务是完成建设的最高要求，必须在超出该修理结构维修能力之前进行增配或升级，即：

3）区域设备使用效率约束

模型优化目标之一是设备的使用效率，设备只有被使用才能发挥其应有的保障效能，但当设备的使用效率低于某一定额时，应减配。即：

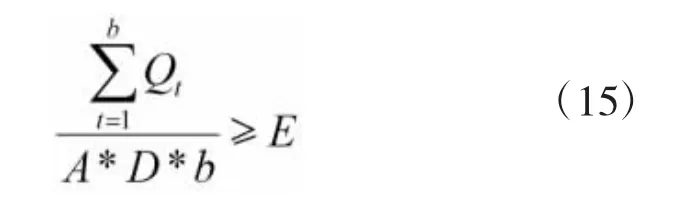
式中，E为建设过程中设定的某设备利用率最低值。

3 求解与验证

3.1 基层级测试设备配置算例

设备优化配置模型求解属于典型的目标优化问题，遗传算法、粒子群算法等很多智能方法可以很好地解决。由基层级测试设备配置模型的目标函数式（4），在已知故障模式数量的前提下，通过调整不同故障模式的维修方式，以达到在计划设备经费下，维修保障时间最短的目的。在确定某种故障模式的维修方式之后，其对应所需的维修设备的种类和数量也是确定，和故障模式的数量呈正比关系。

以某型装甲车辆维修保障为例，需要考虑的故障模式数量为134，在给定设备经费为56万元的情况下，按照第1节方法，通过MATLAB仿真确定各个故障模式的维修以获得最短的平均维修时间，最终确定故障定位测试设备15台，维修调校测试设备11台。

3.2 中继级测试设备配置算例

对于中继级测试设备配置模型的两个目标函数，可将模型中的两个目标赋予相应的偏好系数，进而转化为单目标问题进行求解，结合已有的装甲装备中继级修理结构的地域分布和保障任务量，选定维修任务可达性目标的偏好系数为0.6，使用效率目标偏好系数为0.4。以某新型综合型火控系统综合检测设备（价值230万）为例，针对某地域3个层级4个中继级修理机构进行了基于遗传算法的优化配置MATLAB仿真验证，其中，维修任务量数据依据近3年已有数据采用线性回归预测分析得到。仿真结果表明，提出的模型兼顾了维修任务可达性和设备使用效率，有效可行。

4 结论

针对装甲装备保障测试设备的优化配置问题，分析了研究现状，给出了研究思路；结合装甲装备的维修保障特点，分别建立了保障测试设备的基层级与中继级优化配置模型，通过MATLAB仿真验证了模型的有效性，为实现部队测试设备配置数量、位置和维修效益的协调统一提供了一种新方法。