决策树模型在2型糖尿病预测中的应用

杨　光, 马尔丽

(沈阳师范大学 数学与系统科学学院, 沈阳　110034)

0　引　　言

2型糖尿病是一种代谢性非传染疾病,多数病人在35～40岁之间发病,占糖尿病患者全体的90%左右。2型糖尿病病人产生胰岛素的能力并没有完全失去,一部分患者胰岛素产生甚至过多,但胰岛素的用途却有名无实,因此,糖尿病患者缺乏胰岛素是一种相对的缺乏,可以利用一些特定的口服试剂来激发患者胰岛素的分泌,即使仍有些患者需要按照传统的方式注射胰岛素进行医治。由于糖尿病的遗传易感性的特质,容易在某些特定因素下触动而发病。随着互联网的迅猛成长和人们活动方式的改变及人口老龄化等问题,在世界范围内2型糖尿病的发病率逐年提高,特别是发展中国家增加速度更快(可能到2025年会翻倍),具有流行势态。在全球范围内糖尿病已然变成了在心血管病和肿瘤之后,对人们健康和生命造成危害的重大非传染性疾病。因此,预防2型糖尿病,对于控制糖尿病人数具有重要意义。本文利用数据挖掘ID3算法和分类决策树(CART)的算法构建简单的决策树模型,以此挖掘糖尿病的患病因素,为人们预防和医院的诊断预测工作提供理论依据。

1　材料与方法

1.1　数据来源

资料数据来源于河北省秦皇岛市某医院糖尿病患者病例以及健康人群的体检数据,共1 922例,包含关于2型糖尿病的17项指标:性别、年龄、烟龄、身高与体重的综合指数、收缩压、舒张压、甘油三酯、总胆固醇、低密度脂蛋白、糖尿病家族史、高血压家族史、心脑血管病史、冠心病史、空腹血糖、家族史、既往史、高血压史(SEX,AGE,BMI,SBP,DBP,TG,CHOL,LDL,GLU,FMH,PH,SL,HH,CHDH,CCDH,FHH)[1]。

1.2　方　法

1.2.1分类回归树 (Classification and Regression Trees,CART)

CART决策树算法是在1984年由Breiman提出的,他指出如果当前目标变量是分类变量时,则是分类树,如果目标变量是定量变量时,则为回归树。它以迭代的方式,从树根开始反复建立二叉树[2]。考虑一个具有两类的因变量的两个特征变量的数据。CART算法每次选择一个特征变量将区域分成为两个半平面。经过持续不断地划分之后,特征区间被分成了矩形区域。CART决策树使用基尼指数来划分属性。

1.2.2ID3算法

20世纪70年代机器学习研究者Quinlan在1979年提出构造决策树ID3算法,提出用信息论中的信息增益(information gain)作为决策树属性拆分节点的选择,从而产生分类结构的程序[3]。

1.2.3统计学方法

决策树模型的CART、ID3算法均由R3.4.4实现。

2　结果与分析

2.1　决策树模型

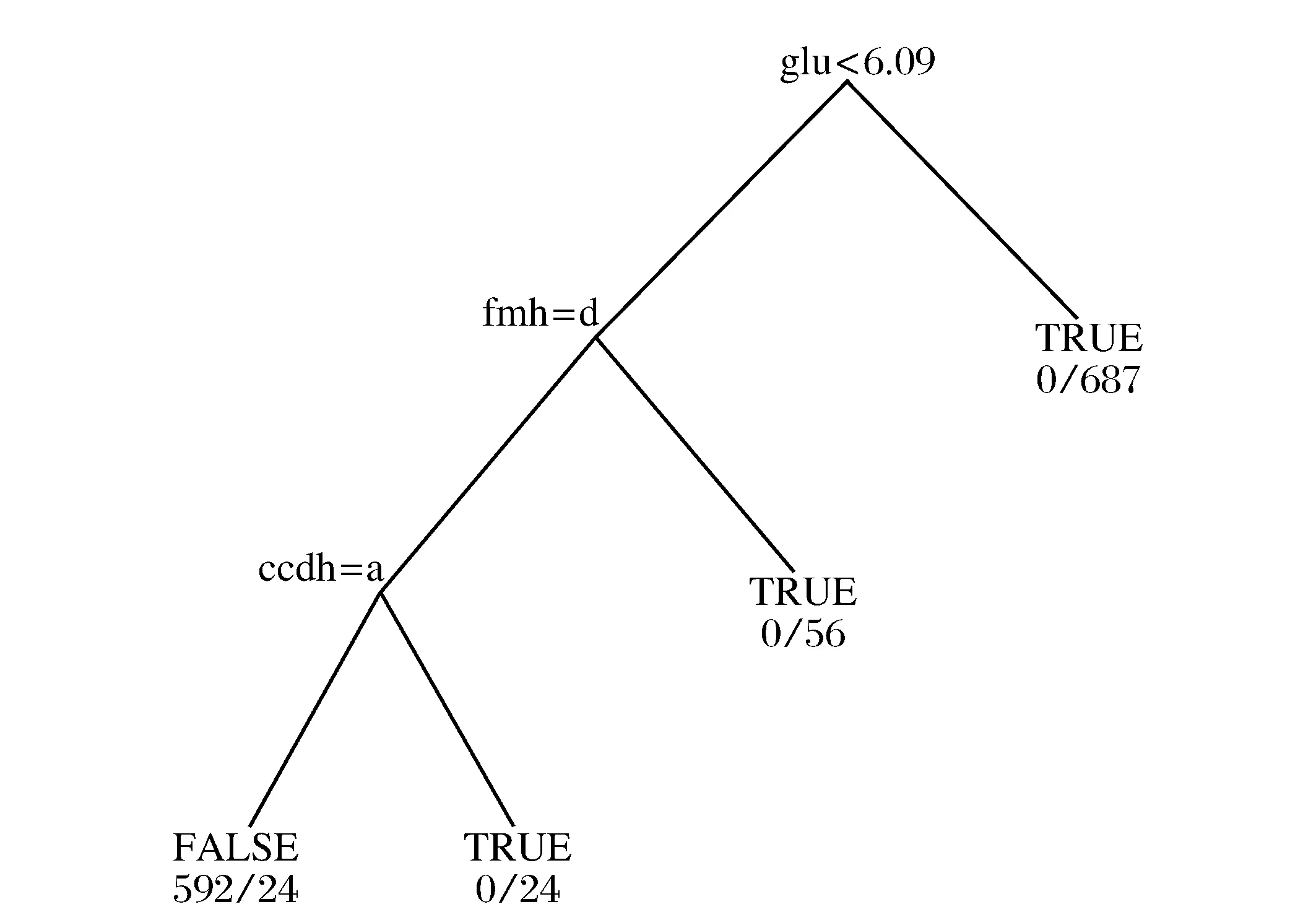
图1　2型糖尿病的ID3算法模型Fig.1　ID3 algorithm model for type 2 diabetes

通过无放回抽样方法在样本中抽取1/4共同构成497例的测试样本, 抽取3/4构成1425例的训练样本。分别用2种算法建立模型,用于建立模型的变量有Sex,Age,BMI,SBP,DBP,TG,CHOL,LDL,GLU,FMH,PH,SL,HH,CHDH,CCDH,FHH共17个变量。决策树的根节点样本总数为1 425,即训练样本总体。

2.1.1ID3决策树模型

ID3模型如图1所示。

在ID3决策树中,左支表示糖尿病患者,其余表示非糖尿病患者。从图1可以看出,如果GLU(空腹血糖)指标<6.09,可以诊断为没有患该病;如果GLU>6.09,并且FMH=false(无糖尿病家族史),可诊断为没有患病;如果有糖尿病家族史,需要观测CCDH(心脑血管家族史),若CCDH=FALSE(没有心脑血管家族史),则没有患病,否则即为患病。

2.1.2CART模型

CART模型如图2所示。

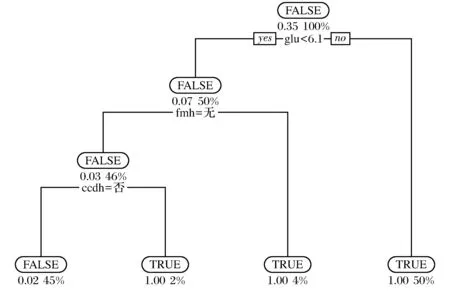
图2　2型糖尿病的CART算法模型Fig.2　CART algorithm model for type 2 diabetes

在CART决策树中,左支表示糖尿病患者,其余表示非糖尿病患者。从图2可以看出,如果GLU(空腹血糖)指标<6.1,可以诊断为没有患该病;如果GLU>6.1,并且FMH=false(无糖尿病家族史),可诊断为没有患病;如果有糖尿病家族史,需要观测CCDH(心脑血管家族史),若CCDH=FALSE(没有心脑血管家族史),则没有患病,否则即为患病。

2.2　模型比较

2.2.1方法比较

决策树算法的核心是拆分属性的判断,本文中的2种算法的拆分原则是不同的。

信息熵(information entropy)是度量样本纯度最常用的一种指标。假定当前样本集合D中第k类样本所占的比例为pk(k=1,2,…,|y|),则D的信息熵为

(1)

Ent(D)的值越小,则D的纯度越高[14]。

假定离散属性a有V个可能的取值,若使用a对样本集D进行划分,则会产生V个分支节点,其中第v个分支节点包含了D中所有在属性a上取值为av的样本,记为Dv。可以根据上式计算出Dv的信息熵,再考虑不同的分支节点所包含的样本数不同,给分支节点赋予权重|Dv|/|D|,即样本数越多的分支节点的影响越大[11-14]。于是可计算出用属性a对样本集D进行划分所取得的信息增益(information gain):

(2)

一般而言,信息增益越大,意味着使用属性a来进行划分所取得的纯度提升越大。本文中的ID3算法就是利用信息增益为准则来选择划分属性的[11-14]。

下面给出CART算法的拆分原理,设拆分变量为j,拆分点为s,定义一对半平面:

Ri(j,s)={X|Xj≤s},R2(j,s)={X|Xj>s}

(3)

分类问题计算出分类变量j和分裂点s,其中k是提前给出的类别数[13]。

(4)

搜寻式(5),求出分裂变量j和分裂点s:

(5)

(6)

找到最佳拆分后,将数据划分为2个结果区域,对每个区域重复拆分过程[13]。最后将空间划分为M个区域R1,R2,…,RM区域Rm对应为势最大的类cm,得到CART预测模型为

(7)

CART使用的是GINI信息度量方法选择变量[13]。

2.2.2结果比较

利用模型对测试样本中的诊断结果进行预测,以评价该模型。预测结果如表1所示。

表1　ID3算法和CART算法的预测结果Tab. 1　Prediction results of the ID3 algorithm and the CART algorithm

从结果表格来看CART模型优于ID3模型。

3　结　　论

糖尿病作为世界第3大威胁人类生命的非传染性疾病,探究糖尿病的发病原因是全世界从事糖尿病医学工作者的重要课题和任务。本文利用决策树算法建立的模型简单明了,解读性强,有一定的临床参考价值[8]。从模型中可以看出空腹血糖、糖尿病家族史、心脑血管既往病史等因素对2型糖尿病发病的重要性,并且通过本文的研究,可以通过空腹血糖、糖尿病家族史、心脑血管既往病史这3个指标来预测糖尿病,避免了很多繁琐的医院检查程序,节约了医疗资源,并且为一些偏远地区的诊断预测提供了指导性建议[9]。

此外,对模型的评价说明利用CART模型挖掘临床检验资料有一定价值,且直观易理解。但由于数据和地域的影响,后续工作仍需要大量的数据和调查资料,合理客观评价模型[1]。