部分连通交叉断层的特征参数及对典型曲线影响研究

曾　杨， 康晓东， 唐恩高， 王旭东

(1.海洋石油高效开发国家重点实验室， 北京　100028； 2.中海油研究总院有限责任公司， 北京　100028)

0　引言

由于储层岩石性质在渗透率、孔隙度上常常表现为非均质性，这种岩石在物性上大的差异常常导致断层的形成.断层的存在最早是通过地震测量来识别，后来，人们发现可以通过试井分析的压力导数曲线反映来识别断层，在此之后学者们对断层的研究也就逐渐丰富[1-3].

由于断层的种类很多，从连通性上可分为封闭断层和部分连通断层，国内外学者Tiab D[4-6]、Yielding G等[7]、Allan U S[8]、Ispas V等[9]、张旭等[10]对断层的试井研究大都集中在封闭断层，而对非封闭断层的研究相对较少；廖新维[11]认为部分连通断层实际上是油层性质在平面上线性不连续的分布，因此他们最先对此类部分连通边界进行研究；刘启国等[12]和罗建新等[13]在刘启国研究的基础上提出了将断层视为线性垂直半渗透边界并且忽略断层内部的储集能力；Anisur等[14]提出了复合油藏中存在部分连通断层的试井解释模型，但是他所求得模型的解是实空间的积分形式并且含有误差函数等特殊函数，不便于考虑井储和表皮系数；张望明等[15]引入偏移函数的概念建立了存在一条线性局部连通断层边界的复合油藏试井解释模型；李传亮[16]提出了不完全镜像反映新方法来研究非封闭断层的试井解释问题.

上述学者的研究并没有同时考虑两条交叉的部分连通断层的影响，且一些求解方法比较复杂.鉴于此，通过沿用Yaxley提出的断层“特殊传导率”的概念，在点源函数的基础上通过镜像反映法建立了存在两条以不同角度(120 °/90 °/60 °等)交叉的部分连通断层试井模型，利用计算机编程绘制了典型曲线，并在此基础上分析部分连通交叉断层的特征参数及其对典型曲线的影响.

1　渗流物理模型

针对无限大地层中存在两条以不同角度(120 °/90 °/60 °等)交叉的部分连通断层的情形，如图1所示，建立数学模型，假设条件如下：

(1)部分连通断层两边为均质油藏，岩石特性及渗透率相同；

(2)油藏流体为单相微可压缩液体，压缩系数及粘度保持不变，流动服从达西定律；

(3)部分连通断层两侧的储层厚度相同；

(4)激动井为定产量线源；

(5)引入“特殊传导率”的概念考虑两个储层区域之间部分连通断层连通性的好坏，部分连通断层边界的流体漏失量与通过的瞬时压力成正比；

(6)忽略重力和毛管力的影响.

(a)120 °的夹角断层

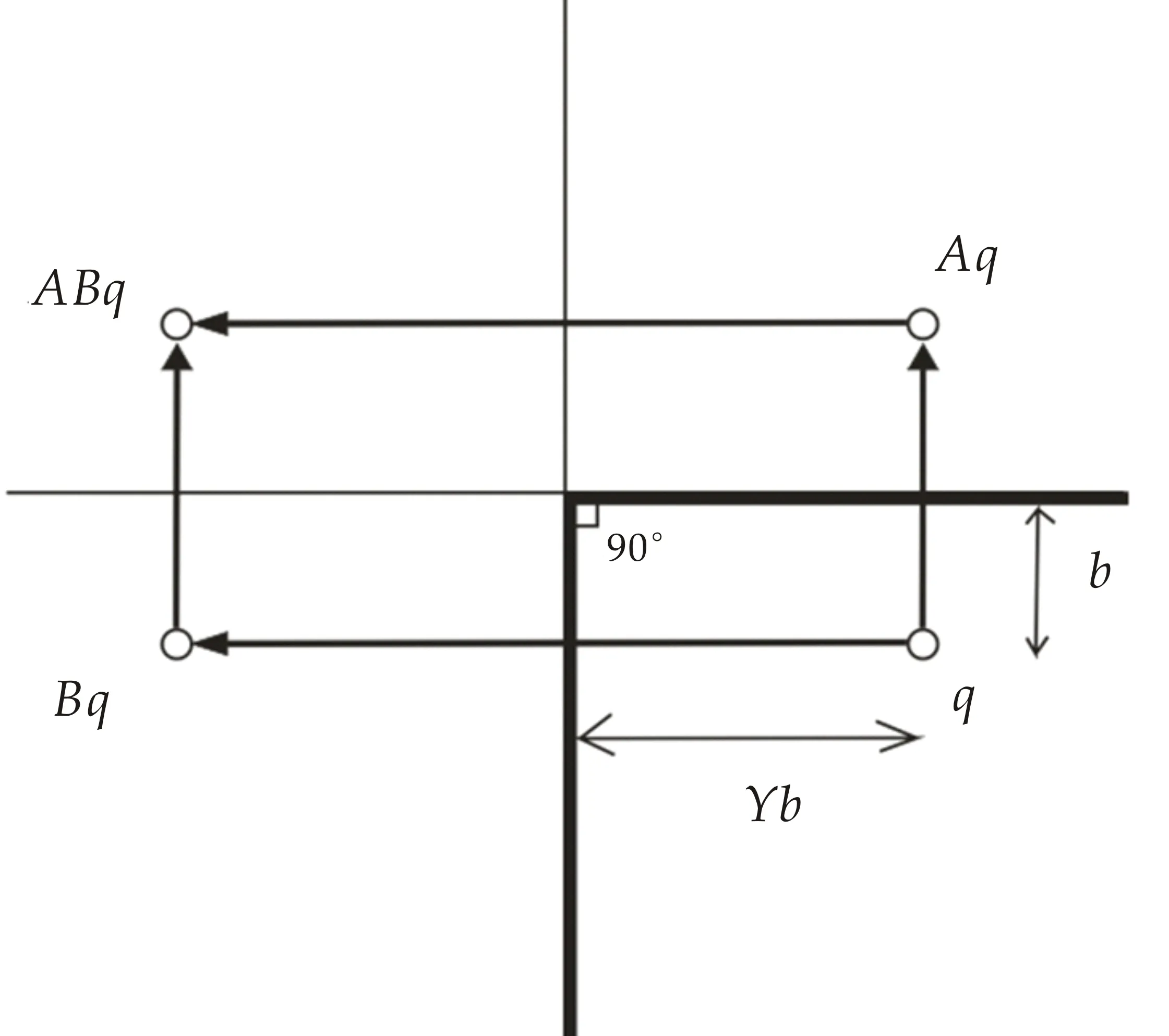
(b)90 °的夹角断层

(c)60 °的夹角断层图1　井位于不同角度交叉断层之间的示意图

2　数学模型的建立及求解

2.1　角度为120 °的部分连通夹角断层

根据图1所建立的坐标系和上述假设条件，引入如下无因次变量.

无因次压力：

(1)

无因次时间：

(2)

无因次距离：

(3)

断层的特殊传导率：

(4)

式(1)～(4)中：pwD—无因次井底流压，无量纲；tD—无因次时间，无量纲；bD—无因次距离，无量纲；αA—断层的特殊传导率，无量纲；pi—原始地层压力，MPa；pw—井底流压，MPa；k—地层渗透率，mD；kf—断层渗透率，mD；h—地层厚度，m；lf—断层宽度，m；q—井流量，m3/d；μ—流体粘度，mPa·s；φ—地层孔隙度，小数；Ct—地层综合压缩系数，MPa-1；rw—井半径，m；b—井距断层的距离，m.

根据镜像反应原理，激动井有两口镜像井，一口镜像井的强度为Aq，另外一口强度为Bq，因此利用叠加原理，可以推导得出此种情况下的生产井井底压力为：

(5)

其中，

式(5)中：Y—距离系数，无量纲；αA1—较近断层的特殊传导率，无量纲；αA2—较远断层的特殊传导率，无量纲.

2.2　角度为90 °的部分连通夹角断层

根据镜像反应原理，可以得到强度分别为Aq、Bq、ABq的三口井，其中最后一口井的镜像反映是两个方向的叠加，两个方向的强度分别为ABq/2，总和即为ABq，利用叠加原理，可以推导得出此种情况下的生产井井底压力为：

(6)

式(6)中：各符号的意义及A、B的表达式与前面相同.

2.3　角度为60 °的部分连通夹角断层

根据镜像反应原理，激动井共有5口镜像井，它到每口镜像井的距离可通过简单的几何运算得到.通过镜像反应，可以得到强度分别为Aq、Bq、ABq、ABq、(AB2+BA2)q/2的五口井.值得注意的是，最后一口井的镜像反应强度是两个方向的叠加，一个方向的强度为AB2q/2，另外一个方向的强度为BA2q/2，因此该井的总强度为(AB2+BA2)q/2.利用叠加原理，可以推导得出此种情况下的生产井井底压力为：

(7)

式(7)中：各符号的意义及A、B的表达式与前面相同.

3　断层的特征参数及其对典型曲线的影响

根据求得的实空间井底压力表达式，首先对压力与时间的函数pwD(tD)进行Laplace数值变换，然后运用Duhamel原理考虑井储和表皮，最后采用Stehfest数值反演方法对其进行拉氏逆变换，可得到实空间内考虑井储和表皮的无因次井底压力数值解，从而可以绘制不同角度交叉的部分连通断层的井底压力响应典型曲线，分析断层的特征参数及其对典型曲线的影响.

3.1　特殊传导率αA的影响

以夹角为120 °为例，为了更清楚地反映压力导数曲线的变化，图2用压力导数半对数图更详细地说明了特殊传导率对典型曲线的影响，井到断层的无因次距离bD=300，距离系数Y=10.

图2中不同的曲线代表了以下不同的油藏特征.特殊传导率越小，断层的连通性越差，反之，特殊传导率越大，断层的连通性越好.如曲线A，当αA1<0.000 1，αA2<0.000 1时，距离较近的断层和距离较远的断层都趋于封闭断层，经过井储和径向流阶段后，压力波首先传播到距离较近的断层，压力导数曲线由0.5水平线上升到值为1的水平线，反映出一条封闭边界的特征，当压力波逐渐传播到距离较远的断层时，压力导数曲线逐渐从值为1的水平线上升到值为1.5水平线，反映出两条夹角为120 °封闭的交叉断层的特征.反之，如曲线I，当αA1>1 000，αA2>1 000时，两条断层都趋于完全连通，经过井储和径向流阶段后压力导数曲线恒定为0.5水平线，反映出无限大均质油藏中线源井的特征.

图2　特殊传导率对压力导数半对数曲线的影响

3.2　夹角θ的影响

图3表示的是夹角θ对存在部分连通交叉断层边界的压力及压力导数典型曲线的影响.从图3可以看出，θ主要影响压力导数曲线第三个水平段的高低，θ越小，相应的压降越大，压力导数曲线则越靠上，第三个水平段的位置就越高.

图3　不同θ影响下的压力和压力导数典型曲线

3.3　距离系数Y的影响

图4以夹角为120 °为例，表示了Y值对存在部分连通交叉断层边界的压力及压力导数典型曲线的影响.从图4可以看出，经过井储和径向流阶段后，由于距离较近的一条断层特殊传导率αA1=0.15，因此压力导数曲线先表现为上翘，当压力波传过这条断层并且还未到达第二条断层时，压力导数曲线表现为一条水平线，该水平线持续时间的长短取决于井到第二条断层的距离，即距离系数Y的值，Y值越大，井到第二条断层的距离越远，水平线持续时间就越长，压力导数曲线出现再次上翘的时间越晚.

图4　不同Y值影响下的压力和压力导数典型曲线

3.4　渗漏系数R的影响

为了更清楚的理解漏失断层的特征，可引入一个漏失系数对这种类型的断层特征进行描述，漏失系数跟断层的漏失量以及断层的特殊传导率有一定的关系，其定义如下：

(8)

当存在两条部分连通交叉断层时，较近一条断层的渗漏系数R1定义同前，较远一条断层的渗漏系数R2定义如下：

(9)

图5展示了不同R值对典型曲线的影响，其中第一条断层的渗漏系数R1一定，第二条断层的渗漏系数R2取不同值，当R2=0时，表明第二条断层基本完全连通，当R2=0.63时，表明第二条断层部分连通，当R2=1时，表明第二条断层完全封闭.

为了找出渗漏系数R与特殊传导率之间的关系，可分以下三种情况来进行讨论：

(1)当第一条断层基本完全连通时(αA1>1 000)，根据前面的公式计算不同αA2值所对应的R2的值；

(2)当第一条断层部分连通时(αA1=0.2)，根据前面的公式计算不同αA2值所对应的R2的值；

(3)当第一条断层基本完全封闭时(αA1=0)，根据前面的公式计算不同αA2值所对应的R2的值.

图5　不同R值影响下的压力和压力导数曲线

图6　渗漏系数R与特殊传导率αA之间的关系

(10)

则：

(11)

4　结论

(1)建立了存在两条以不同角度交叉的部分连通断层边界的试井解释新模型，采用镜像反应方法和叠加原理进行求解，求解方法简单.

(2)断层的“特殊传导率”越小，断层的连通性越差；夹角θ主要影响压力导数曲线第三个水平段的高低，θ越小压力导数曲线则越靠上；Y值越大，井到第二条断层的距离越远，压力导数曲线出现再次上翘的时间越晚；渗漏系数R越小，断层的连通性越好.

(3)引入“特殊传导率”的概念，推导了特殊传导率与渗漏系数的反比关系式.