基于脉冲压缩与载波恢复的直接扩频信号相位差提取方法研究

张　毅　李喜民　李　康

(西安电子工程研究所　西安　710100)

0　引言

相位干涉测向技术是根据测向天线对不同到达方向电磁波的相位响应的不同实现目标方向的测量。影响干涉仪测向精度的因素主要包括基线长度的准确度、频率稳定度、鉴相精度等，通过采用精密机加和高稳定度频综可以忽略基线长度和频率稳定度对测向精度的影响，鉴相精度成为影响测向精度的主要因素。

现代雷达往往采用复杂的信号形式以保证对目标的检测特性与低截获性能，本文以某相位干涉测向系统所采用的直接扩频信号为基础，讨论了针对该信号形式的相位差测量方法，通过仿真给出了两种方法在信噪比与多普勒频率变化时的相位差提取精度的仿真结果。

1　解扩FFT载波恢复鉴相法

解扩FFT载波恢复鉴相法的原理框图如图1所示。鉴相环路主要由下变频、低通滤波、相关脉压、恒虚警、解扩、FFT及相位差计算等组成。

相位差提取过程如下：由接收机输出的A、B两路中频信号经A/D采样后进行正交下变频与低通滤波处理，选取A路信号与事先存储的本地PN码进行相关脉冲压缩，脉压结果通过恒虚警检测以获得相关峰的位置。随后控制本地PN码与下变频后的基带扩频信号进行解扩处理以获得载波信号，分别对两路载波进行FFT，经过共轭复乘后求取两路信号的相位差。

图1　解扩FFT载波恢复鉴相法原理图

设A、B两路信号分别为：

A=PA×PN(t-tc)×cos(ωt+φA)+nA(t)
B=PB×PN(t-tc)×cos(ωt+φB)+nB(t)

(1)

其中PA、PB分别为A、B两路信号的幅度，φA、φB分别为A、B两路信号的初相，nA、nB分别为A、B两路信号的噪声。

设NCO的频率为ωc，采用正交处理，NCO可表示为：

C=e-j(ωct+φC)

(2)

经过下变频和低通滤波后A路信号可表示为：

IA(i)=PA×PN(iTs)×
cos[(ω-ωc)iTs+φA-φC]+nA(i)
QA(i)=PA×PN(iTs)×
sin[(ω-ωc)iTs+φA-φC]+nA(i)

(3)

B路信号可表示为：

IB(i)=PB×PN(iTs)×
cos[(ω-ωc)iTs+φB-φC]+nB(i)
QB(i)=PB×PN(iTs)×
sin[(ω-ωc)iTs+φB-φC]+nB(i)

(4)

选取A通道的基带数据与本地PN码相关处理后可得：

IA(i)=PAsinc[Td(ω-ωc)/2]×
cos[(φA-φC)Ts]+nA(i)
QA(i)=PAsinc[Td(ω-ωc)/2]×
sin[(φA-φC)Ts]+nA(i)

(5)

SA=PAej[(ω-ωc)iTs+φA]
SB=PBej[(ω-ωc)iTs+φB]

(6)

对两路信号进行FFT后经过共轭复乘可得：

SA-B=kej[φA-φB]

(7)

求取SA-B的相角可得A、B两路信号的相位差：Δφ=φA-φB。

2　相关脉冲压缩峰值鉴相法

相关脉冲压缩峰值鉴相法的原理框图如下图所示。鉴相环路主要由下变频、低通滤波、相关脉压、恒虚警及相位差计算等组成。

相位差提取过程如下：由接收机输出的A、B两路中频信号经A/D采样后进行正交下变频与低通滤波处理，随后与事先存储的本地PN码进行相关脉冲压缩，脉压结果通过恒虚警检测以获得相关峰的位置，分别在A、B两路脉压结果的对应位置取出相关峰值的复数形式结果，经过共轭复乘后求取两路信号的相位差。

图2　相关脉冲压缩峰值鉴相法原理图

A、B两通道的基带数据与本地PN码相关处理后可得：

IA(i)=PAsinc[Td(ω-ωc)/2]×
cos[(φA-φC)Ts]+nA(i)
QA(i)=PAsinc[Td(ω-ωc)/2]×
sin[(φA-φC)Ts]+nA(i)
IB(i)=PBsinc[Td(ω-ωc)/2]×
cos[(φB-φC)Ts]+nB(i)
QB(i)=PBsinc[Td(ω-ωc)/2]×
sin[(φB-φC)Ts]+nB(i)

(8)

MA=kA[cos[(φA-φC)Ts]+jsin[(φA-φC)Ts]]
MB=kB[cos[(φB-φC)Ts]+jsin[(φB-φC)Ts]]

(9)

其中kA=PAsinc[Td(ω-ωc)/2]；kB=PBsinc[Td(ω-ωc)/2]；

对上述两项进行共轭复乘可得：

MA-B=kej(φA-φB)

(10)

求取MA-B的相角可得A、B两路信号的相位差：Δφ=φA-φB。

3　仿真与精度分析

为验证以上两种鉴相方法的鉴相精度，搭建的验证平台如图3所示，仿真中的主要参数如表1所示。

图3　仿真数据采集框图

序号PN码型GOLD1PN码周期5112PN码速率10MHz3接收机中频频率60 MHz4采样率100MHz5信噪比0～-15dB6多普勒频率范围±6KHz

两种鉴相方法仿真的采集数据与仿真过程数据如图4所示。

3.1　不同信噪比条件下的鉴相精度仿真

为验证两种算法的鉴相精度，由信号源和噪声发生器分别产生信号和噪声，通过示波器采集了信噪比分别为0～-15dB的中频信号，如图5、图6所示，通过仿真分析了两种算法的鉴相精度。为隔离多普勒频率对鉴相精度分析的影响，在进行信噪比仿真时取多普勒频率为0。

图4　实际采集的仿真数据

图5　0～-15dB信噪比时相关脉冲压缩峰值鉴相法仿真结果

图6　0～-15dB信噪比时解扩FFT载波恢复鉴相法仿真结果

3.2　不同多普勒频率条件下的鉴相精度仿真

多普勒频率会使得脉压峰值降低，影响恒虚警检测。为减小多普勒频率对脉压结果的影响，采用了多通道多普勒频率补偿技术。补偿后的多普勒频率范围在±6KHz以内，故以下仿真的多普勒频率范围取±6KHz。如图7、图8所示，同样为隔离信噪比对鉴相精度分析的影响，在进行多普勒频率仿真时取信噪比为0dB。

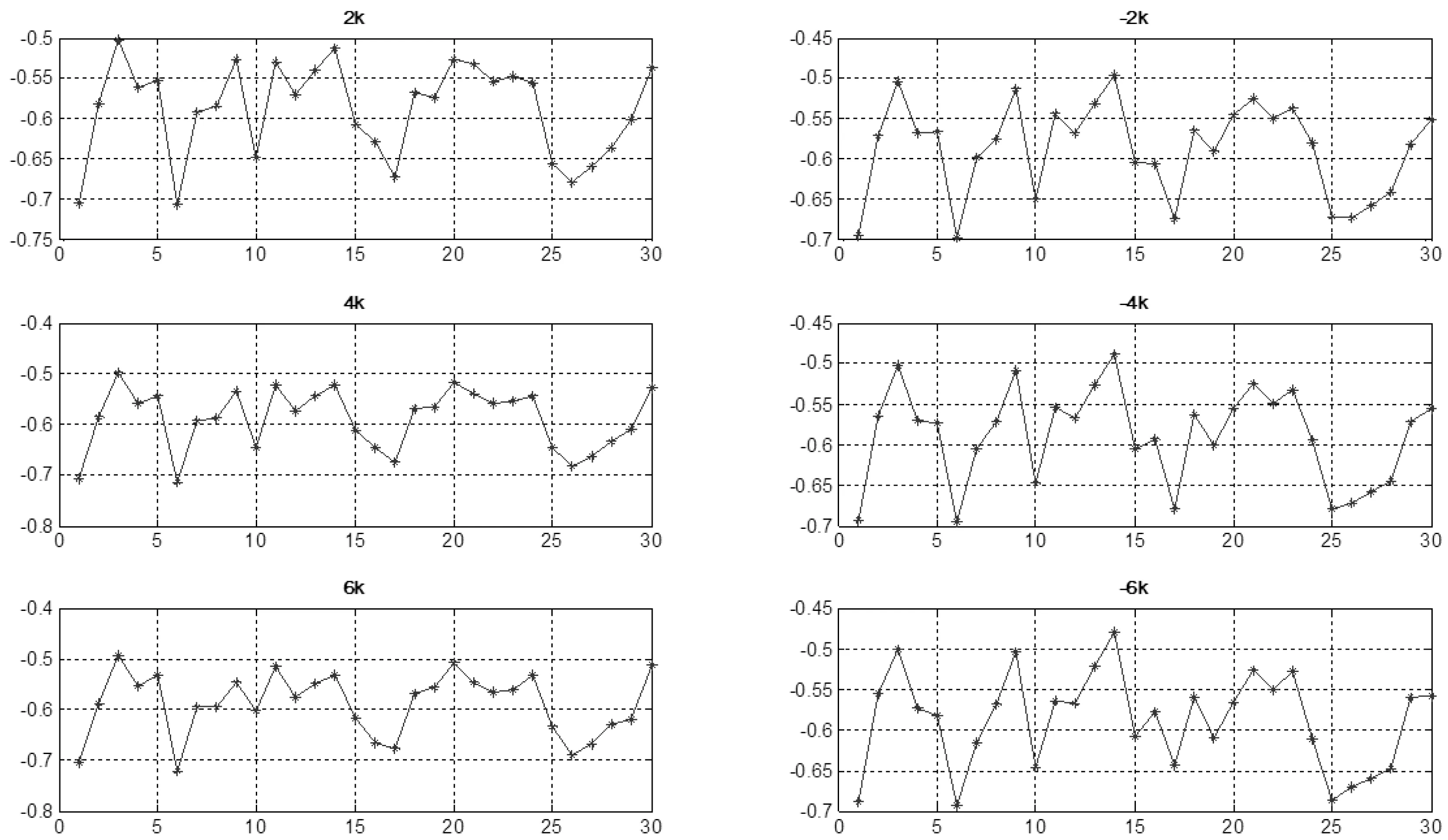
图7　±6KHz多普勒时相关脉冲压缩峰值鉴相法仿真结果

图8　±6KHz多普勒时解扩FFT载波恢复鉴相法仿真结果

4　结束语

本文针对直接扩频信号的相位差提取问题，对相关脉冲压缩峰值鉴相法和解扩FFT载波恢复鉴相法的原理进行了介绍，通过对模型的仿真计算得出以下结论：

1)相关脉冲压缩峰值鉴相法是通过对脉冲压缩峰值的检测在时域完成相位差的提取，解扩FFT

载波恢复鉴相法是通过对直扩信号的解扩以获得载波信号再在频域完成相位差的提取，两种方法均能够完成直接扩频信号的相位差提取；

2)通过对不同信噪比条件下两种方法鉴相精度的仿真可以看出，二者的鉴相精度基本相当，当信噪比低于-12dB时，相关脉冲压缩峰值鉴相法的精度略高于解扩FFT载波恢复鉴相法；

3)通过多通道多普勒频率补偿技术，在±6KHz的多普勒频率范围内，两种鉴相方法的鉴相精度不受多普勒频率的影响；

4)通过对两种方法的原理分析可以看出，相关脉冲压缩峰值鉴相法的环路组成相对简单，仅需获得脉冲压缩的峰值即可完成相位差的提取。而解扩FFT载波恢复鉴相法需要在完成脉冲压缩峰值的恒虚警检测后精确调整本地PN码的初始相位，才能通过解扩获得载波信号，工程实现的复杂度略大。