时变磁化等离子体的LTJEC-FDTD方法研究

席阳红，谢国大，徐　辉，黄志祥，吴先良，王丽华

(安徽大学电子信息工程学院，安徽合肥　230601)

1　引　言

等离子体是物质的第4种状态，具有许多独特的物理化学特性，是宇宙间绝大部分物质存在的状态。自1879年发现以来，等离子体的研究一直是学者们关注的焦点，其在微电子、金属、聚合物、污染治理等诸多领域都有着重要的应用价值［1-2］。然而现实中等离子体频率会随周围温度、时间、空间、外加磁场的变化而变化。外加磁场下的时变磁化等离子体更是一种复杂的各向异性色散介质，对入射电磁波有折射、碰撞吸收、共振吸收等特性，这些特性使得时变磁化等离子体可运用在很多的实际应用中，如等离子体滤波器和隐身技术等方面。同时，时变磁化等离子体也是一种产生太赫兹波源的方法。虽然目前该方法并未被实际应用，但是具有非常大的发展潜力。目前对于等离子体的研究主要是局限于时变等离子体或者磁化等离子体，对于将两种情况结合起来的时变磁化等离子体的研究并不多。因此研究时变磁化等离子的特性以及时变磁化等离子体产生太赫兹波源的可行性尤为重要。

目前研究磁化等离子体介质电磁特性的时域数值方法主要为时域有限差分(Finite difference time domain，FDTD)方法，这是由于FDTD方法一次时域计算后用傅里叶变换就能得到整个频域电磁散射，非常适合宽频计算。递归卷积算法、分段线性电流密度递推卷积算法、电流密度递推卷积时域有限差分(JEC-FDTD)、电流密度拉普拉斯时域有限差分(CDLT-FDTD)算法以及基于拉普拉斯变换的电流密度卷积时域有限差分(LTJECFDTD)是目前比较广泛用于磁化等离子体介质的FDTD 算法［3-4］。其中，LTJEC-FDTD 算法是一种将CDLT-FDTD和JEC-FDTD结合并改进的FDTD算法。该算法并没有规避掉复杂的卷积，而是将电流密度卷积简化处理并与拉普拉斯变换完美结合［5-6］，同时迭代公式也较为简洁，在编程上计算效率更高。1997年，Steven A Cummer分析了非磁化等离子体的FDTD算法［7］。2009年，Kalluri应用CDLT-FDTD算法研究电磁波在一维时变磁化等离子体中的传播特性［8］。2015年，杨利霞应用LTJEC-FDTD算法分析了磁化等离子体电磁波传播特性，但未进一步分析利用时变磁化等离子体产生太赫兹波［5］。

本文应用LTJEC-FDTD算法，对一维时变磁化等离子体进行分析。首先介绍了LTJEC-FDTD算法的基本原理，并模拟了调制的微分高斯脉冲垂直入射磁化等离子体层。通过对比LTJEC-FDTD和CDLT-FDTD两种算法下的反射系数及编程上的运行时间，验证了LTJEC-FDTD算法的正确性及高计算效率性。然后研究了Whistler波在一维时变磁化等离子体中的传播特性。结果表明，当离子体频率随时间指数衰减后，Whistler波的频率上升、极化方式不变，同时电场加强、磁场减弱。最后通过优化后的等离子体碰撞频率、等离子体频率、以及电子回旋频率，进一步提升了Whistler波的输出频率并得到频率为300 GHz的圆极化太赫兹波，为磁化等离子体产生太赫兹波提供了一定的理论依据。

2　LTJEC-FDTD算法

2.1　 LTJEC-FDTD算法基本原理

在各向异性等离子体介质中，相关的本构方程如下［9-11］:

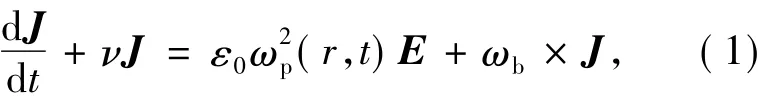
式中，E为电场强度;J为电流体密度;ε0和μ0分别为真空中的介电常数和导磁率;ν为电子碰撞频率;ωp(r，t)表示时变等离子体频率;ωb=(eB0/me)为电子回旋频率，B0为外部静态磁场，e和me分别为电子电量和电子质量。对于一维的TEM波，式(1)可写成矩阵形式:

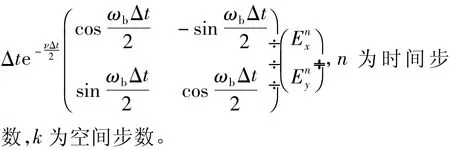
2.2　数值验证

LTJEC-FDTD和CDLT-FDTD两种算法下模拟TEM波垂直入射到磁化等离子体中的电磁传播，入射波采用调制的微分高斯脉冲［12］，传播模型如图1所示。空间网格总数为600，磁化等离子体层由网格数200～400构成。计算空间步长Δz为7.5μm，时间步长为Δt为1.25 ps［13-15］。此外在计算空间的两端各设10个网格的PML吸收边界用于吸收截断边界产生的反射［16-18］，其余网格为自由空间。磁化等离子体频率ωp=30×2πGrad/s，电子回旋频率ωb=10 Grad/s，电子碰撞频率 ν=5 Grad/s。

图2(a)、(b)分别为右旋圆极化(RCP)波和左旋圆极化(LCP)波穿过磁化等离子体层的反射系数。结果表明，LTJEC-FDTD和CDLT-FDTD两种算法下的反射系数基本吻合，验证了该算法的正确性。图2(c)为两种算法的FDTD计算效率对比。为了更明显地看出两种算法的计算效率，图2(c)的纵坐标采用10t，其中t为FDTD的计算时间。从对比中可以看出，在相同的时间步长下，LTJEC-FDTD算法运行所用的时间要明显小于CDLT-FDTD算法所用的时间，计算效率更高。

图1　等离子体平板传播模型

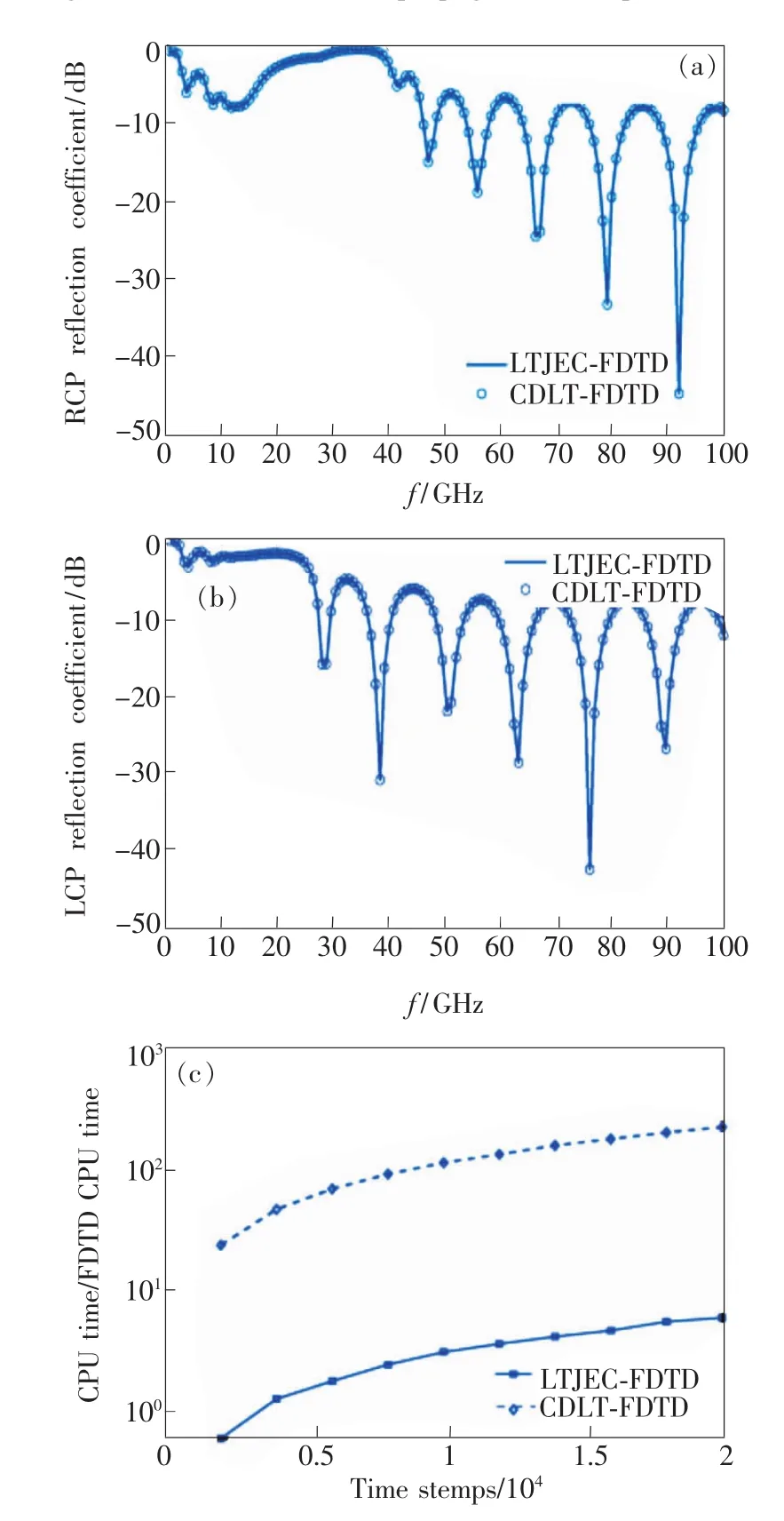
图2　反射系数图。(a)RCP波反射系数振幅图;(b)LCP波反射系数振幅图;(c)计算效率。

3　一维时变磁化等离子体的电磁特性

图3为填充时变磁化等离子体的一维矩形金属谐振腔，电磁波传输方向与外加磁场的方向均为+z方向。这部分中LTJEC-FDTD的计算空间步长Δz为0.012 cm，时间步长 Δt为 0.000 2 ns。在等离子体变化之前(t＜0)，内加RCP驻波如下:

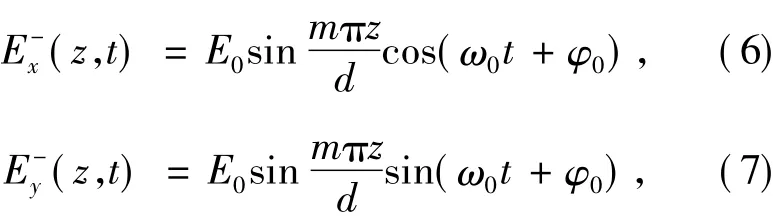
其中m=1;0为相位角;d为金属板的距离，与波源频率ω0有如下关系:

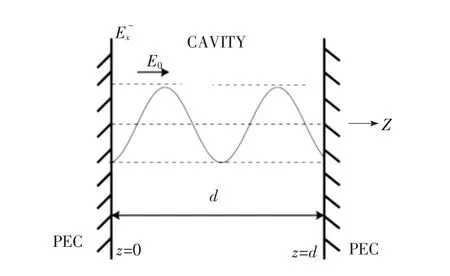
图3　一维矩形金属谐振腔计算模型

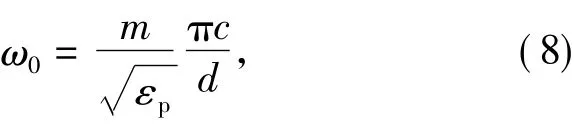
εp为磁化等离子体中的相对介电常数［19］:

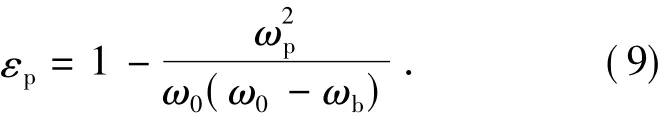
3.1　 LTJEC-FDTD在时变磁化等离子体中的正确性验证

采用图3的计算模型，进一步验证LTJEC-FDTD在时变磁化等离子体中的正确性。磁化等离子体随时间变化规律如下:

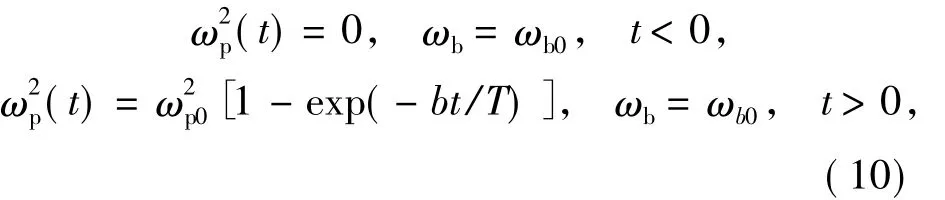
其中ωp0和ωb0分别为等离子频率和电子回旋频率的初始值，b为衰减系数，T为RCP波的周期。选取驻波源频率ω0=2π×10 Grad/s，磁化等离子体频率ωp0=2π ×17.32 Grad/s，电子回旋频率 ωb=2π ×10 Grad/s，电子碰撞频率ν=0，衰减系数b=100。

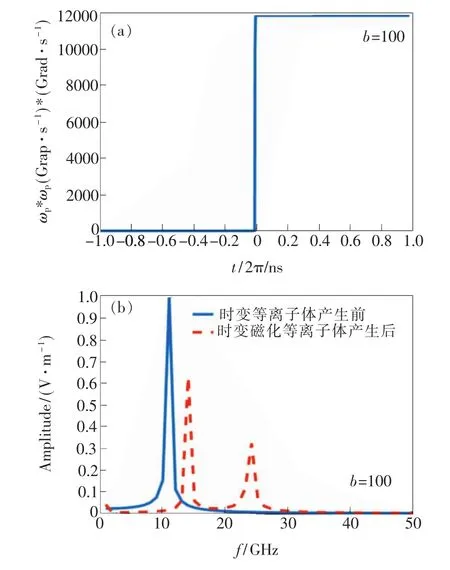
图4　时变磁化等离子体中z=d/2处电场抽样FDTD结果。(a)等离子体频率随时间变化图;(b)加入时变磁化等离子体前后金属矩阵腔体的谐振频率。

图4(a)为时变磁化等离子体随时间变化图。如图所示，在t＜0时等离子体频率ωp0=0，即腔体内为真空;t＞0后等离子频率随时间指数增长，增长系数为b=100。图4(b)为在z=d/2处抽样的电场值随等离子体变化前后的频域结果。如图所示，当等离子体频率增长后谐振腔内出现了 3 个谐振频率，分别为 f1=2.4，17，24.6 GHz。这3个谐振频率与文献［5］中的理论值一致，从而验证了LTJEC-FDTD方法计算时变磁化等离子体的正确性。

3.2　W histler波在时变磁化等离子体中的传播特性

对于式(9)，当 ω0ωb、ωp02ω0ωb0时，相对介电常数εp可以近似为:

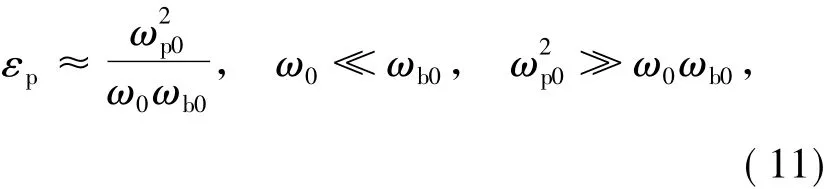
这样的右旋极化波叫做Whistler波［20］。

时变磁化等离子体频率在时域上从稳定不变到随时间指数衰减，变化规律如下:

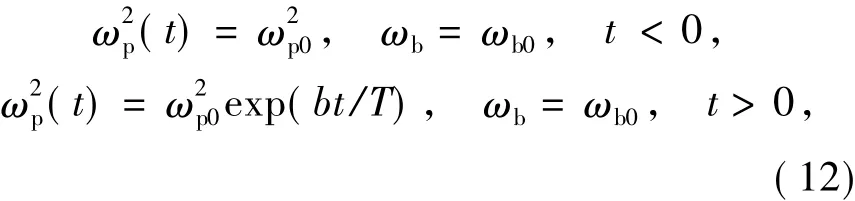
其中ωp0和ωb0分别为等离子频率和电子回旋频率的初始值，b为衰减系数，T为RCP波的周期。取频率为ω0=1 Grad/s的Whistler波作为入射波，研究其在时变磁化等离子体中传播的传播特性。磁化等离子体频率ωp0=200 Grad/s，电子回旋频率ωb0=100 Grad/s，电子碰撞频率ν=0。

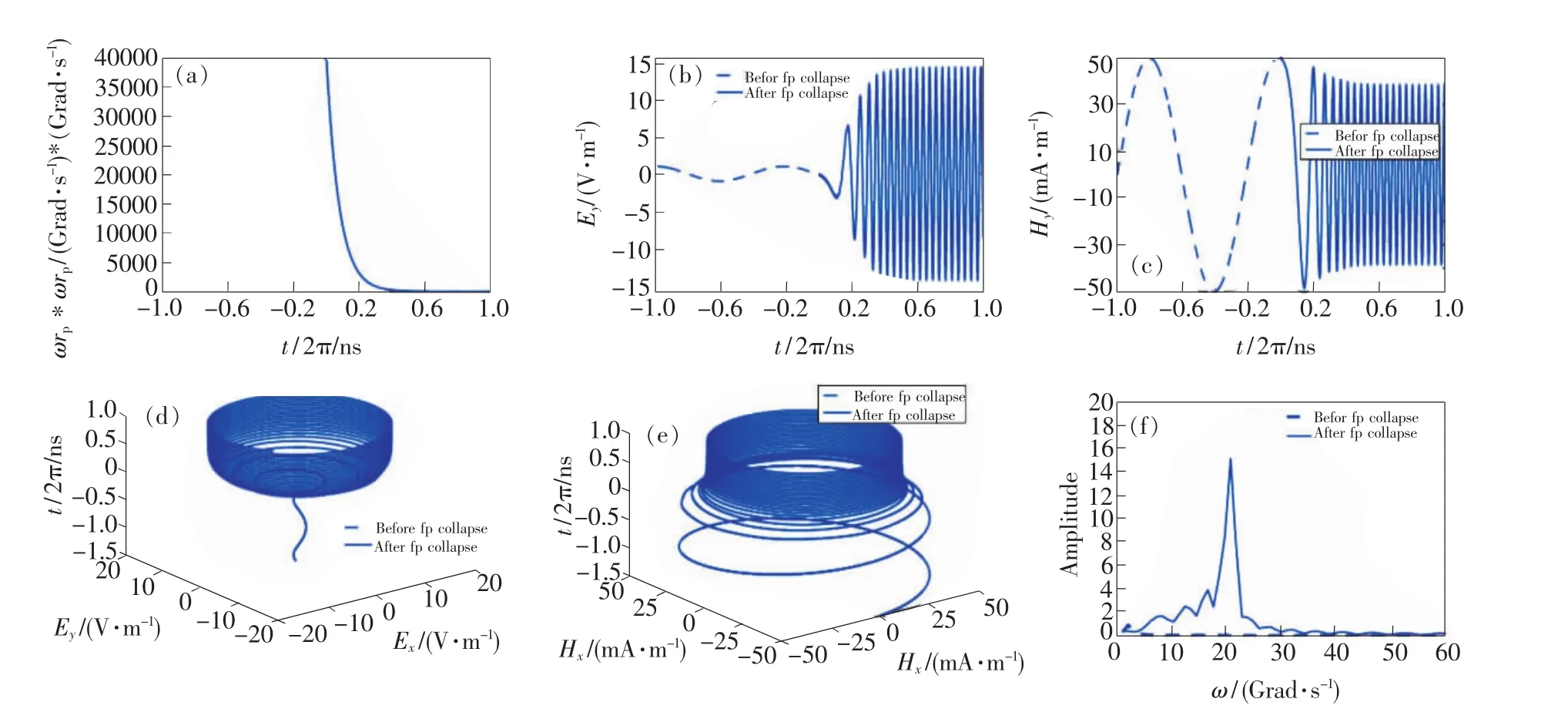
在z=d/2和z≈0处分别对电场和磁场进行抽样，LTJEC-FDTD的抽样结果如图5所示。图5(a)为衰减系数b=10的等离子体频率时域变化情况，由稳定不变到指数衰减。图5(b)和图5(c)分别为z=d/2处电场以及z≈0处磁场的时域抽样结果。由图可知，电场频率和磁场频率在磁化等离子体频率衰减后均有所上升，频率由原来的1 Grad/s增为20 Grad/s，该频率增长系数与磁化等离子体中的折射率nR=(εp)1/2一致;同时电场的振幅增大到原来的15倍，而磁场的振幅略有减小。图4(d)和图4(e)分别为电场及磁场的极化方式变化情况，由图可知，Whistler波极化方式不变，仍为圆极化螺旋形式。通常情况下电磁波在静态场下的等离子体中传播时，波的极化是不断变化的。但是当外部磁场的方向垂直波的传播方向(横向模式)或沿着波的传播方向(纵向模式)时，波的极化就会稳定不变［21］。图5(f)为电场的频域结果，从中可以更清楚地看出电场的频率由1 Grad/s提升到了20 Grad/s并且振幅增大为原来的15倍。

从能量的角度分析上述结果，衰减的磁化等离子体会引起等离子体中电流的消失，消失电流的磁能转化为波的电能和磁能，这些改变使波源的频率上升，并增强了电场和能量密度［22-23］。

3.3　时变磁化等离子体产生太赫兹波的分析

时变磁化等离子体中频率上升的关键条件就是折射率nR＞1。当ω0与ωp0近似，即在谐振频率附近时，频率上升的更大。此外电子回旋频率ν也有着不可忽视的影响。我们在3.2的基础上进一步提升输出波的频率，研究时变磁化等离子体产生太赫兹波。这里减小ωb0/ω0的比率放宽公式(13)的第一条件，同时增大ωp0的值加强第二条件:

取输入波的频率为ω0=10 Grad/s，电子回旋频率ωb0=50 Grad/s，磁化等离子体频率 ωp0=600 Grad/s。此外增加电子碰撞频率的影响，取ν=0.01ωp0。

图6(a)表示衰减系数b=1 000时的等离子体密度的变化情况，实质上波源频率的上升与等离子体消失的快慢并无关系［24］。图6(b)和图6(c)分别为z=d/2处电场以及z≈0处磁场的时域抽样结果。由图可知，通过减小 ωb/ω0的比率，增大ωp和ν的值，输出波的频率在等离子体频率衰减后有了进一步的提升，由原来的10 Grad/s上升为300 Grad/s，频率增长系数为30。图6(d)为电磁的极化方式的变化。由图可知，输出波仍为右旋圆极化波。图6(e)和图6(f)分别为电场和磁场在频域上的变化情况，从图中可以更明显地看出Whistler波的输出频率为300 Grad/s，并且磁场的幅值进一步衰减。这部分结果表明，优化后的时变磁化等离子体参数进一步提高了输出波的频率，最后得到了频率为300 Grad/s的圆极化太赫兹波，从而在理论上验证了时变磁化等离子体可产生太赫兹波。这部分中的时变磁化等离子体参数参考了文献［25］中所做的相关实验，证明了该理论方法在实验上的可行性。

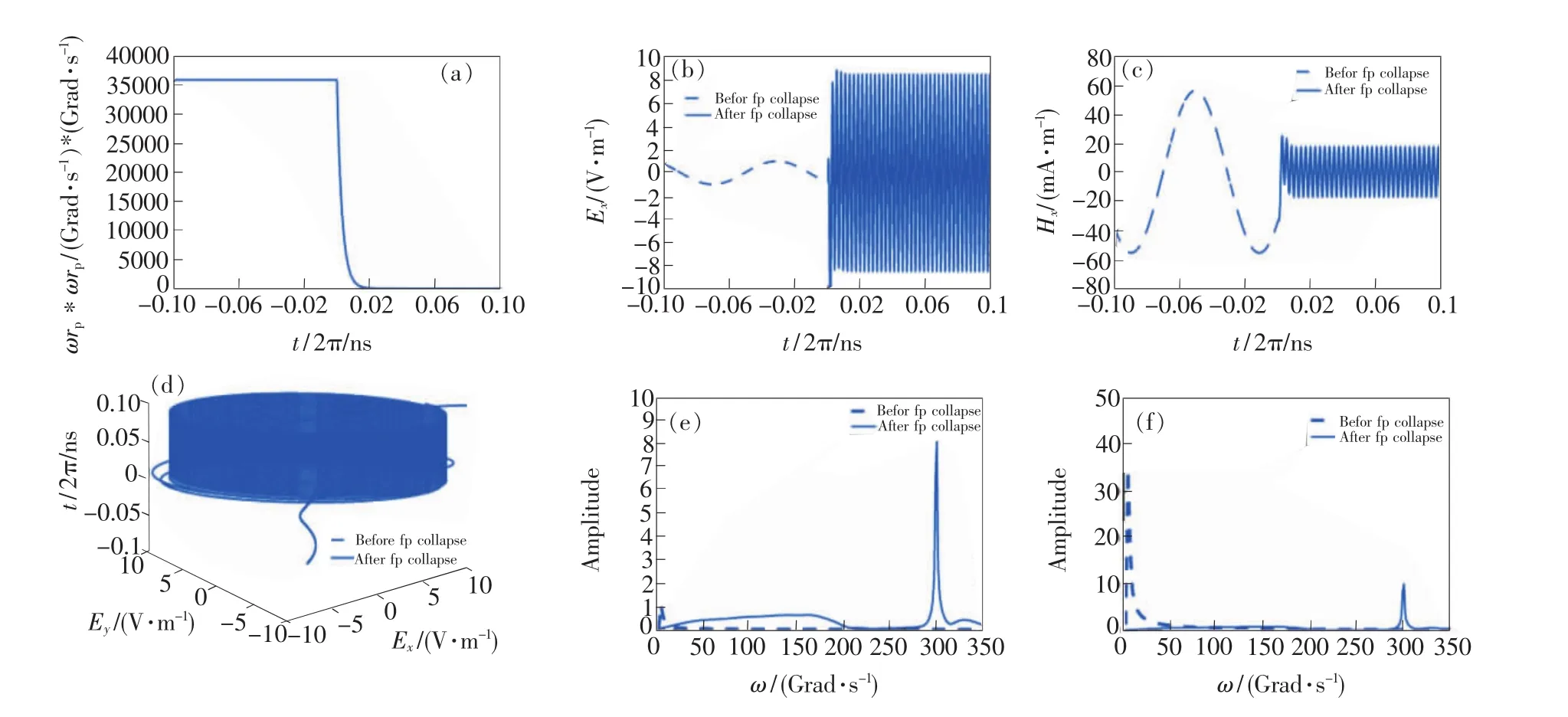
图6　时变磁化等离子体中z=d/2处电场和z≈0处磁场的抽样FDTD结果。(a)等离子体频率随时间变化图;(b)电场时域变化图;(c)磁场时域变化图;(d)电场极化方式变化图;(e)磁场极化方式变化图;(f)电场频域变化图。

4　结　论

本文应用LTJEC-FDTD算法从频域和时域上分析了时变磁化等离子体的电磁特性。首先模拟了调制的高斯脉冲在磁化等离子体中的频域的电磁反射系数，从频域角度验证了LTJEC-FDTD算法的准确性和高效性.然后研究了Whistler驻波在一维时变磁化等离子体中的传播特性以及太赫兹波的产生。仿真结果表明，时变磁化等离子体相当于频率转换器，提升了输入波的频率，同时加强电场减弱磁场。等离子体频率、电子回旋频率、电子碰撞频率及衰减系数都是输出波的影响因素。最后通过优化后的参数得到了频率为300 GHz的太赫兹波，从理论上验证了时变磁化等离子体可产生太赫兹波，这些理论结果对变频系统的发展及太赫兹源的产生具有一定的指导意义。