基于改进Fisher准则、VMD、距离相关系数和 核极限学习机的轴承故障诊断
宋坤骏, 丁建明, 林建辉
(西南交通大学 牵引动力国家重点实验室, 成都 610031)
滚动轴承作为机械设备中常见且高故障率的部件,其状态的及时监测和故障的准确诊断具有十分重要的意义。当前振动信号故障特征提取手法有很多,包括快速傅里叶变换,小波变换,Wigner-Ville分布,由Huang等人[1]提出的经验模态分解(EMD)和Dragomiretskiy等人[2]提出的变分模态分解(VMD)等。就EMD和VMD两者的特点而言,EMD算法因为缺乏坚实的数学基础面临着模态混叠,端点效应等问题。VMD算法源自严格的数学推导,基本消除了模态混叠现象,同时由于VMD可看成一组自适应的维纳滤波器,因而对噪声具有较高的鲁棒性。VMD在实际工程应用中面临的主要问题在于算法参数的选取。针对这一问题,文献[3]提出了以去噪后的信噪比和均方差为优化目标采用遗传算法优化VMD参数。文献[4]提出了以模态分量的包络熵值最小化为优化目标采用遗传算法优化VMD参数。上述两种优化方法均从信号预处理的角度出发,没有结合分类算法,而参数选择对于分类算法的效果实际上也有很大影响,典型例子当属支持向量机(SVM)。文献[5]采用差分进化算法通过最小化SVM在验证集上的泛化误差优化SVM的参数,该方法的特点是原理较为简单,优化结果准确,缺点是计算量偏大。文献[6]为减小计算量,提出了基于Fisher准则和最大熵原理的SVM核参数选取方法。文中借鉴其思想并加以提升,提出了以改进的核空间多类别Fisher准则为优化目标,优化小波核极限学习机的核参数ω和a。
故障诊断流程如下:首先通过模态中心频率错开原则以及信噪比最大原则确定VMD预设模态数K和二次惩罚参数α。然后将信号通过VMD分解为若干模态分量,提取各分量的峭度,中心频率和同原信号的距离相关系数作为输入核极限学习机的特征向量,并使用模拟退火粒子群算法基于改进的核空间Fisher准则优化小波核极限学习机的核参数ω和a。最后使用参数优化的小波核极限学习机对轴承的4种故障进行分类辨识。
1 变分模态分解(VMD)
VMD算法能够非迭代地求出非平稳信号的各个本征模态函数,不仅避免了EMD等迭代型算法的筛分停止准则选取,模态混叠等问题,也有效提高了分解效率。同EMD不同的是,VMD需要预先设定希望获得的本征模态函数(IMF)分量数K,它通过最小化K个模态函数的带宽和构造变分问题。求取模态函数带宽和的手段是:先进行Hilbert变换求出边际谱,然后乘以指数因子将模态函数的频谱移动到待求的中心频率,最后计算上述信号的梯度平方L2范数作为带宽的估计。整个需要求解的约束变分模型如下:
(1)
式中uk(t)为第k个IMF分量(1≤k≤K),ωk为其待求的中心频率。Dragomiretskiy和Zosso通过引入二次惩罚因子α和Lagrange乘子λ消除约束,将上述极小值问题转化为求解下述增广Lagrange函数的鞍点
(2)
这里二次惩罚项可以提升收敛性能和对噪声的鲁棒性,拉氏乘子使得重构约束条件得到严格满足。可通过交替方向乘子法(ADMM)求解上述问题,每次求解一个变量,其他变量视为已知,可以在频域求得第n+1次迭代的结果为
(3)
(4)
(2)n=n+1迭代开始
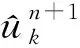
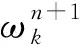
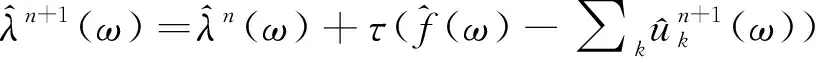
2 小波核极限学习机[7]
极限学习机[8]是一种单隐层前馈神经网络的特殊训练算法,该算法最大的特点在于大大减少了需要迭代计算求解的权值和偏置个数,将原两层权值的迭代求解问题转换为通过最小二乘法求解最后一层的输出权值。因而不仅大大加快了训练速度,而且非但没有丧失泛化能力反而有所提升。单隐层前馈神经网络的输出层公式为
=h(x)β
(5)
这里h(x)=[h1(x),h2(x),…,hL(x)]T和β=[β1,β2,…,βL]T分别是隐藏层激活函数向量和隐藏层输出权值,ai和bi分别是输入层权值和偏置,β由正则化的Moore-Penorse广义逆给出为
βt=HT(I/C+HHT)-1T
(6)
上式中关于N个输入样本[x1,x2,…,xN]的隐层输出矩阵H定义为
(7)
其中L是隐层神经元数,而关于N个输入样本的训练数据目标矩阵则由下式定义
(8)
其中m是输出维数。由以上公式可以得出ELM算法的训练流程图如下:
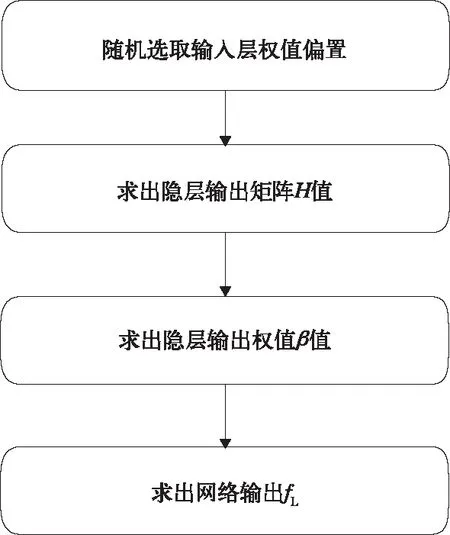
图1 极限学习机训练流程
由图1知,原始极限学习机算法需要随机选取输入层权值ai和输入层偏置bi,手动选取隐层神经元数L,给算法带来很大不确定性。仔细分析可以发现,这些参数的作用仅在于设定隐层特征映射h(x)的具体形式,而实际上由式(5)和式(6)可知,在输出函数中无需知道h(x)的具体形式,只需知道内积h(xi)·h(xj)的形式即可,如下式所示:
fL(x)=h(x)β=[K(x,x1),…,K(x,xN)](1/C+
G)-1T
(9)

(10)
小波核函数中的参数ω和a将通过文中的改进Fisher准则采用模拟退火粒子群算法予以联合优化。
3 改进的Fisher准则
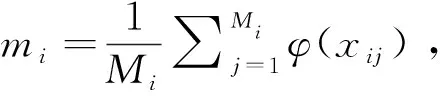
(11)
文中Fisher准则用于指导核函数参数的选择,也就是用来挑选隐层非线性特征映射φ,为此需要将核空间的类间离散度和类内离散度用核函数表达出来,这是可以办到的,结果为
(12)
(13)
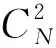
(14)
以上S2/S1的表达式中,xir代表第i类的第r个样本点。
实际运用时为了计算方便和精度考虑,可以等价地最小化S1-S2。
4 模拟退火粒子群算法
粒子群算法(PSO)[10]是一种在复杂解空间中通过粒子群的运动近似搜索最优解的启发式算法,具有易于实现和收敛速度快的优点,但在进化后期容易出现粒子趋同,收敛停滞,优化精度不理想等现象。考虑到模拟退火算法具有较强的概率突变跳出局部最优解的能力,提出一种结合模拟退火和粒子群算法的混合优化算法。基于模拟退火的粒子群算法的步骤如下
① 随机初始化种群中各个微粒的位置xi和速度vi
② 初始化pi为粒子i当前最优适应度值对应的位置,初始化pg为当前所有粒子中最优个体的位置
③ 确定初始温度,一般采用如下初始温度和退温方式:
T(t+1)=λT(t)T(0)=f(pg)/ln5
(15)
④ 按照下列公式更新各个微粒的速度和位置:
vij(t+1)=φ{vij(t)+c1r1[pij-xij(t)]+
c2r2[pgj-xij(t)]}
(16)
xij(t+1)=xij(t)+vij(t+1)
(17)
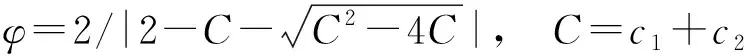
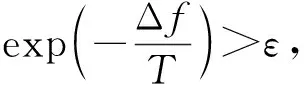
⑥ 按照各微粒的新位置更新个体最优位置pi和群体最优位置pg
⑦ 在同一温度下,步骤④~⑥重复L次
⑧ 更新温度
⑨ 若达到最大迭代次数,则停止搜索,输出群体最优值,否则转④
5 故障特征提取
距离相关系数[11]是传统Pearson线性相关系数的一种改进,它基于两个随机向量X和Y的联合分布fXY(x,y)和各自分布的乘积fX(x)fY(y)之间的函数距离,可以度量两个随机向量X和Y之间的非线性相关关系。随机向量X和Y的样本Xk和Xk,(k=1,2,…,n)之间的经验距离相关系数定义为
(18)
上式中若分母为0,则dCor(X,Y)=0,其中经验距离协方差dCov(X,Y)定义为
(19)
和式中的有关项定义为
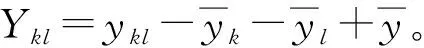
6 试验数据分析
文中所用故障轴承振动加速度数据来自美国Case Western Reserve University,数据的采样频率为12 kHz,轴承转速为1 797 r/min,对应旋转频率30 Hz。轴承损伤点是用电火花机人工加工形成的,其直径为0.017 8 cm。测试轴承是SKF6205型深球沟轴承的驱动端轴承。采集了外圈,内圈,滚动体故障和正常情况共4种信号。每种信号取长度为2 048的一段作为样本进行特征提取。
以内圈信号为例,首先基于任意两个模态分量的中心频率不能太过接近,即最小中心频率间隔不能小于最大中心频率间隔的20%定出VMD算法的模态数K=4。K=2~5的情况下根据采样频率可计算出内圈故障信号各模态中心频率如表1所示,由表1可见当K=5时最后两个模态的中心频率较为接近,可能发生模态混淆,故取K=4。
VMD的二次惩罚参数α的最优值可以通过信噪比和模态带宽方面的考虑求得。首先来考虑信噪比,这里采用的降噪方案基于上节的距离相关系数,具体方法是求出各个模态分量同原信号的距离相关系数,舍去小于最大相关系数25%的较小相关系数对应的IMF分量,剩余的IMF分量求和重构即完成降噪过程。例如表2给出了内圈故障信号在α=2 000,K=4,τ=0的情况下各模态同原信号的距离相关系数dCor值。
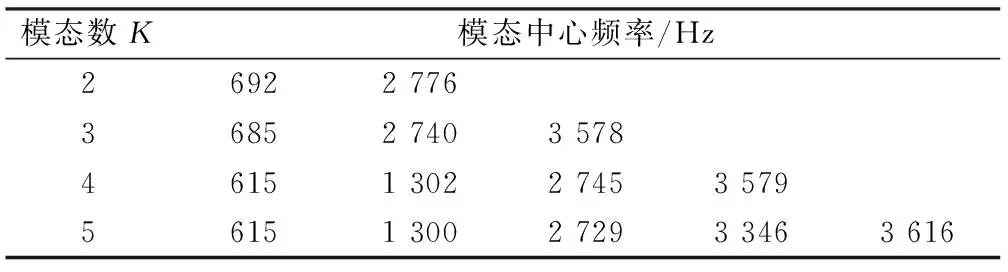
表1 内圈故障信号各IMF中心频率

表2 内圈故障信号各IMF同原 信号距离相关系数
由于表中最小的相关系数大于最大相关系数的25%,所以没有模态被舍去,即便如此,这4个模态重构求和后并不精确等于原信号。这是因为以去噪而非重构原信号为目的,为了将噪声排除在重构和外,已将施加重构约束的拉氏乘子λ(t)的更新系数τ的值设为0(见VMD算法流程第5步)。根据重构前后信号u(t)和f(t),可以算出信噪比
(20)
计算发现信噪比随着惩罚参数增大而减小且递减速率渐趋缓慢(图2)。由于VMD可以看成自适应的维纳滤波器组,因而信噪比跟模态分量带宽一样均随惩罚参数变小而变大,两者变化趋势是一致的。
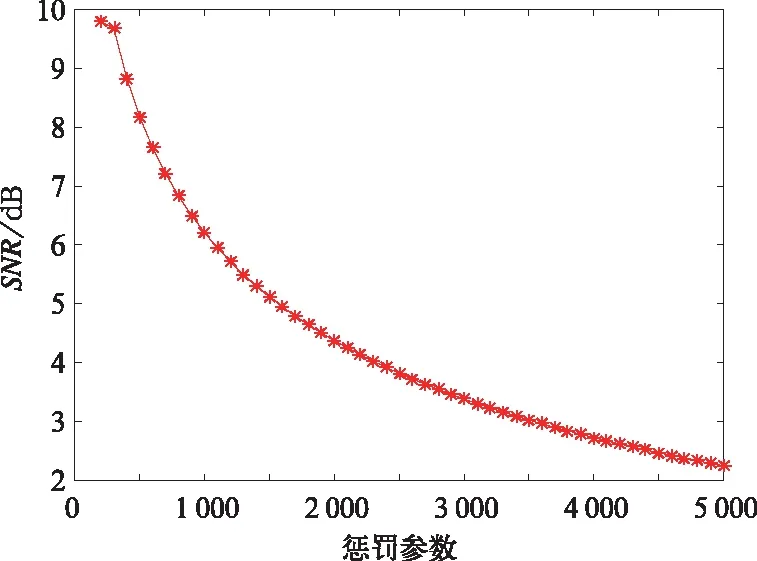
图2 不同惩罚参数α下VMD滤波后信噪比
由于参数α越小信噪比越大且各模态的带宽越大,因此应当选取各模态无频带交叠时的最小α值。各模态频带不发生交叠的条件是任两模态中心频率间隔大于两模态带宽之和的一半。由此可以计算出满足上述条件的最小α取值为300。
获得VMD算法关键参数K和α之后,将信号做VMD分解,分解所得IMF分量的时域波形如图3所示。图3中模态的冲击成分以200个采样点为周期,对应频率为60 Hz,这不是故障的特征频率而是轴承旋转频率的倍频,所以难以从时域信号判断故障类型。随后提取各模态的峭度,模态中心频率和同原信号的距离相关系数作为输入小波核极限学习机的特征向量。核极限学习机的核参数ω和a使用核空间的改进Fisher准则予以优化。求解此优化问题用到模拟退火粒子群算法,算法参数为粒子数N=40,学习因子c1=2.05,c2=2.05,收缩因子φ=0.729,最大迭代次数M=100,退火常数λ=0.5。优化计算得到的小波核参数的最优值为ω=1.232,a=34.69。小波核函数指数因子中的参数a的增加会增加该指数因子,从而增大了核空间的内积,直观上提高了核空间的线性区分度。
为说明文中提出的算法的效果,运行3组对比试验:(1)同样的粒子群算法参数但使用原始Fisher准则,优化得到的小波核参数的最优值为ω=0.002 55,a=4.275。(2)将同一信号进行EMD分解,提取分解后同原信号距离相关系数最大的前4个IMF分量的峭度,平均瞬时频率以及距离相关系数后输入参数同为ω=1.232,a=34.69的核极限学习机中。(3)同一组信号VMD分解,但是用普通的相关系数而非距离相关系数作为特征。
全部4组试验条件下测试集准确率随正则化参数变化的曲线如图4所示,由图4看出,4组试验条件下测试集准确率均随着正则化参数C增大而增大,且增幅渐趋平缓。使用VMD分解且用改进的Fisher准则优化的小波核极限学习机的分类准确率最高,说明Fisher准则改进后确实起到了进一步改良非线性特征映射,使得映射后不同类别的样本点在核空间中更为有效分离的作用。造成这种现象的原因是改进的Fisher准则通过类间最小差异度和类内最大差异度定义的类内和类间离散度比原始Fisher准则通过样本均值定义的类内和类间离散度更为合理,考虑了类中样本点分布的极差,顾及了分布的全局性质。而以样本均值为代表计算的离散度体现的是个别样本点的局部性质。因而改进的Fisher准则能够在核空间获得更为优良的线性可分性。使用普通相关系数而非距离相关系数作为特征的试验组准确率排在最后,这是因为距离相关系数比起通常的只能度量线性关系的线性相关系数更好地反映了随机变量间的非线性依赖关系,是一种更为有效的刻画随机变量间独立性的统计量。
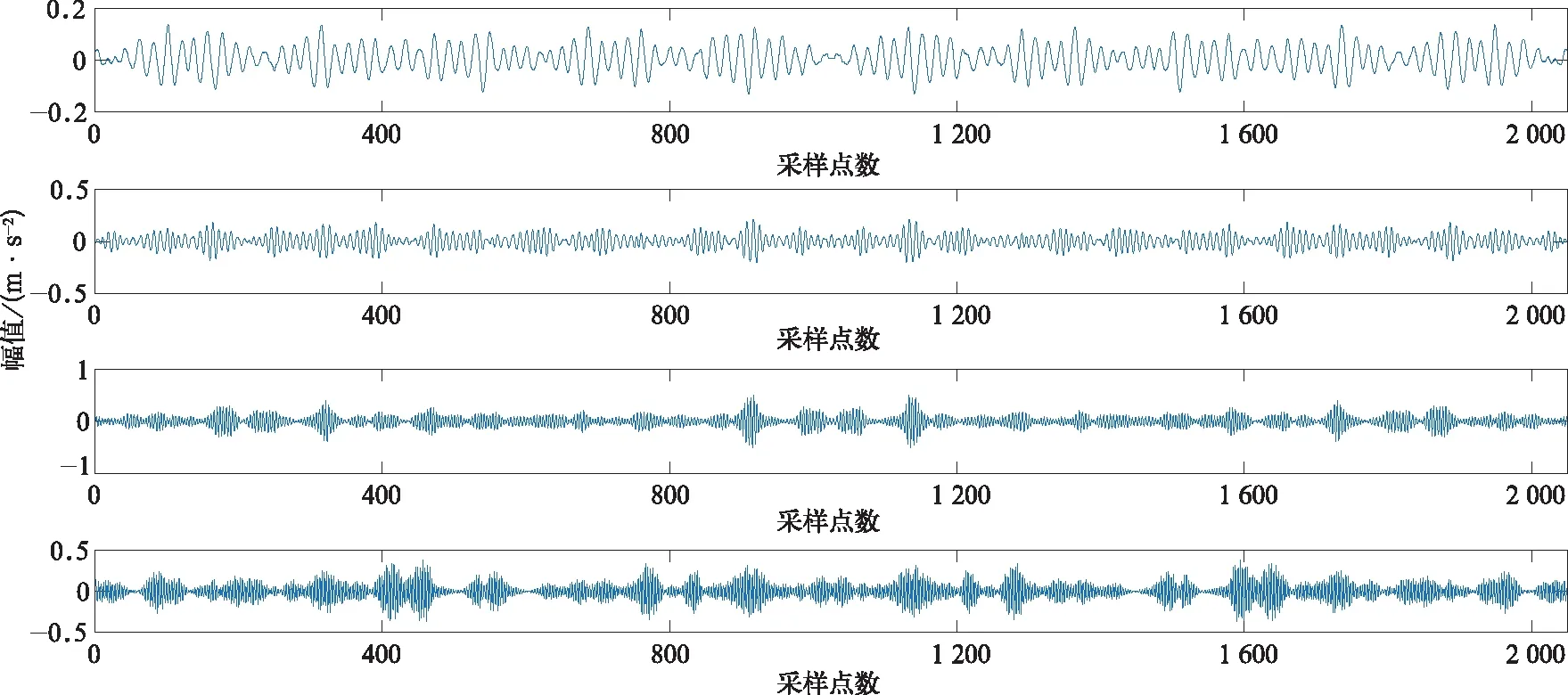
图3 α=300 K=4时VMD 4个模态的时域图
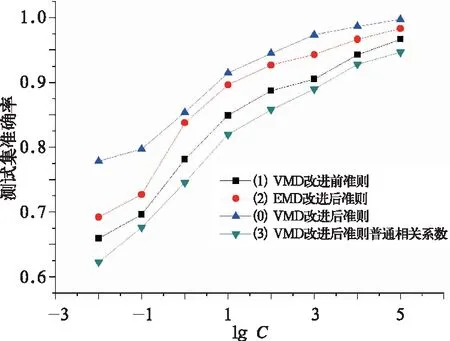
图4 测试集准确率随正则化 参数C变化曲线
为了研究文中所提算法对噪声的鲁棒性,对4种工况振动信号加入信噪比为5 dB的高斯白噪声后再进行VMD分解,特征抽取和状态识别。表3和表4分别为加入噪声前后的混淆矩阵数据。
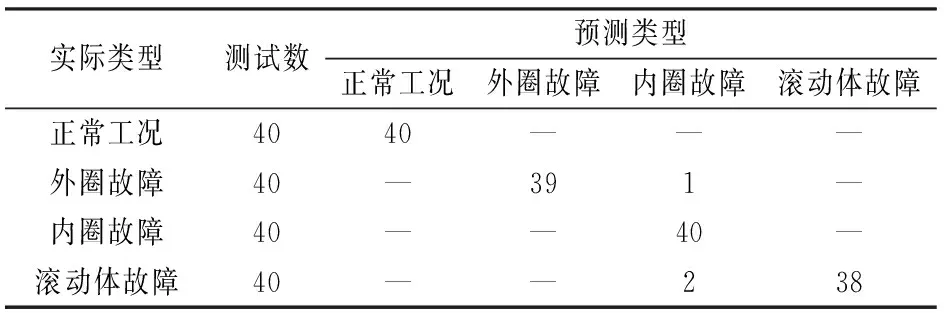
表3 算法在添加高斯白噪声前混淆矩阵

表4 算法在添加高斯白噪声后混淆矩阵
由表4可知,加入高斯白噪声后,文中算法对正常工况,外圈故障,内圈故障和滚动体故障的识别率分别为97.5%,95%,100%和95%,平均识别率仍然达到了96.875%,表明VMD分解方法具有良好的噪声鲁棒性。作为对比,表5和表6是采用EMD分解方法的相应混淆矩阵,可以看到噪声的加入严重影响了EMD的分类准确率。EMD分解方法不能很好地应用于实际中富含噪声的真实信号。
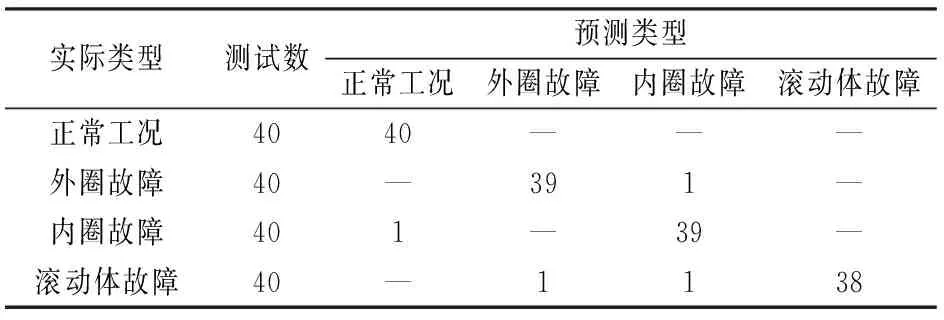
表5 采用EMD分解的算法在添加 高斯白噪声前混淆矩阵

表6 采用EMD分解的算法在添加 高斯白噪声后混淆矩阵
为了说明核极限学习机相对同样基于核方法的支持向量机学习算法的优越性,表7给出了基于VMD分解和SVM分类算法的混淆矩阵数据。这里在4类数据的每2类之间训练一个Morlet小波核SVM分类器,核参数采用改进的Fisher准则予以优化,样本最后的分类结果是在2类分类中“胜出”数最大的类别。
从表7可知SVM平均识别率为95.625%,同表3对比可知在准确率方面略低于核极限学习机。表8给出了不同的训练样本数占总样本数百分比情况下基于交叉验证和基于改进的核空间Fisher准则的SVM 核参数寻优耗时和准确率数据。
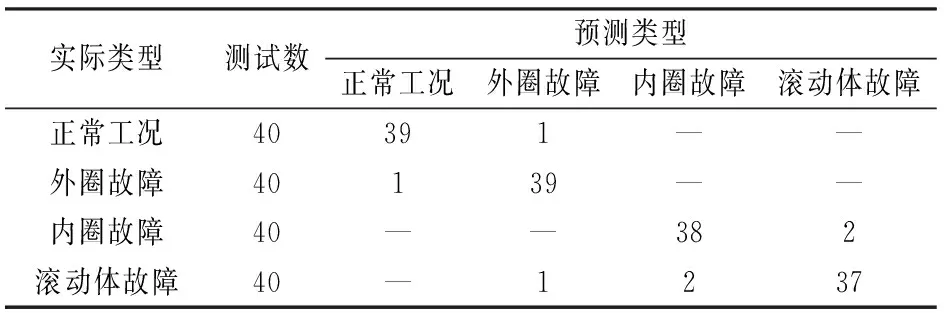
表7 采用VMD分解的SVM算法的混淆矩阵
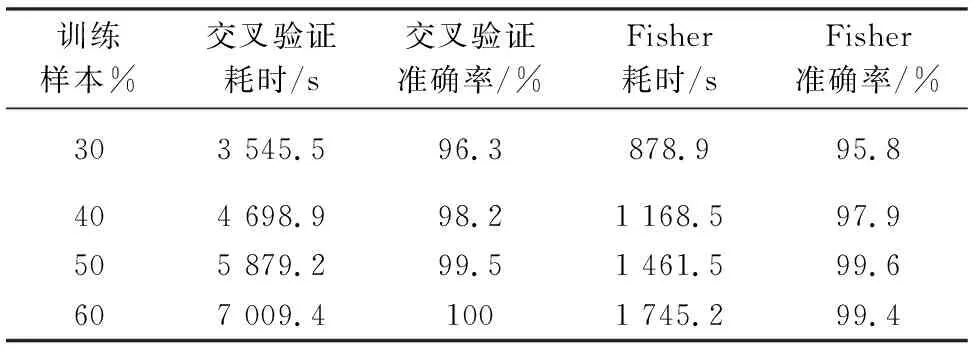
表8 基于交叉验证和基于Fisher准则的 SVM核参数优化的准确率和耗时数据
从表8看出改进的核空间的Fisher准则相比交叉验证的参数优化方法而言在准确率上相差不多但是参数优化的耗时有明显下降。所以就SVM算法来说,改进的Fisher准则不失为一种快速的优选参数的手段。对于核极限学习算法而言,由于核极限学习机的训练速度远快于SVM,因而改进的Fisher准则在耗时上的优势无法发挥,但是对于小样本训练集的情形,交叉验证方法不再适用,而改进的Fisher准则仍然可以在小样本情形下指导SVM和核极限学习机的核参数优化。
7 结 论
针对核极限学习机在轴承故障诊断中遇到的参数选取问题提出了一种采用改进后核空间中的Fisher准则进行参数优选的方案,针对振动信号信噪比低的问题提出了一种基于变分模态分解和距离相关系数的滤波和特征提取方法。通过实验数据的分析,得出以下结论:
(1) 距离相关系数能够很好地度量随机变量间的非线性相关关系,在滤波和特征提取方面的效果要优于线性相关系数。
(2) VMD分解方法有效避免了EMD分解的模态混叠现象,而且对噪声有较高鲁棒性,在轴承故障信号分析领域有广阔的应用前景。
(3) 提出的改进的Fisher准则相比原始的Fisher准则提升了分类算法的泛化性能,相比交叉验证法降低了参数优化耗时,适用于SVM算法的参数优化以及小样本情形下核极限学习算法的参数优化。

