车轮扁疤对高速列车齿轮箱动态特性影响分析*

邹航宇， 张卫华， 王志伟

(西南交通大学　牵引动力国家重点实验室， 成都 610031)

在高速列车的走行部件中，齿轮箱传动系统是实现整车牵引传动的关键部件，其微小的破坏对整车和乘客生命安全的威胁都将是致命的。我国新型高速列车的齿轮箱的悬挂方式与传统牵引电机的刚性轴悬式结构类似，其大齿轮压装在车轴上，小齿轮端通过C型托架与转向架相连[1]。这样的悬挂方式结构简单、工作稳定且维修方便。但齿轮传动系统的工作条件较差，来自轮轨的激扰将很容易传递到齿轮箱上，对齿轮传动系统和箱体造成巨大影响。轮轨激扰一方面来自于轨道的道岔冲击、轨道不平顺激扰等，另一方面则来自于车轮本身，如车轮失圆等。车轮扁疤是车轮失圆的一种典型工况，它对轮轨接触和整车动力学性能有着巨大的影响，国内外学者在这方面做了大量工作[2-4]。在这些研究中，多是针对轮轨响应的分析，少有考虑其对齿轮驱动装置的影响。实际上，由于齿轮箱的安装特性，齿轮驱动装置除受其自激振动产生的对垂向和点头振动的影响外[5]，更多的还受轮轨激扰的影响。在车轮扁疤发生时，在与齿轮箱同样安装在车轴上的轴箱上能够检测到剧烈的加速度冲击[6]，而由于脉冲激扰能够激起广泛频率范围的响应，这甚至将引起具有薄壁轻质特性的齿轮箱箱体的共振。鉴于以往对车轮失圆与齿轮箱传动系统响应结合研究的欠缺和对工程中箱体裂纹起因的探索，针对车轮扁疤工况下的齿轮传动系统和齿轮箱体动态响应的研究是有必要的。

由于高速列车齿轮传动系统的动态特性和结构特殊性，难以通过传感器直接实测其动态响应参数。故本文建立了包含齿轮传动系统和柔性齿轮箱的高速列车整车刚柔耦合模型，并建立车轮扁疤模型以考虑故障工况。通过仿真计算，研究车轮扁疤对高速列车齿轮啮合和箱体应力状态的影响，为高速列车齿轮箱故障模拟及故障溯源提供参考。

1　计算模型

1.1　齿轮传动系统模型

高速列车的齿轮传动系统为斜齿轮传动系统，由于齿轮啮合产生的轴向动态分力，轴向振动是斜齿轮副区别于直齿轮副的重要特征。又由于其传动轴和支承的弹性变形，齿轮传动系统除具有弯曲振动、扭转振动和轴向振动以外，还将因动态啮合分力导致齿轮副产生扭摆振动，因此需建立弯-扭-轴-摆耦合振动模型。在以往的研究中，对此只考虑了8个自由度[7]，但在文中的仿真计算中，需要针对工程实际工况建立12自由度的完整模型。为了简化计算，不考虑齿面摩擦的弹性变形，并用对称布置的支承模拟传动轴的弯曲弹性，斜齿轮副12自由度动力学模型如图1所示。

在此12自由度模型中，系统的广义位移列阵可以表示为：

δ={xp，yp，zp，θpx，θpy，θpz，xg，yg，zg，θpx，θpy，θpz}

(1)

其中，xi、yi、zi(i=p,g)为主、从动齿轮中心Op、Og在x、y、z向的平动位移，θpx，θpy，θpz(i=p，g)分别为为主、从动齿轮中心点绕x、y轴的摆动角位移和绕z轴

图1　斜齿轮副弯-扭-轴-摆 耦合动力学模型

的扭转振动角位移。

将啮合阻尼和啮合刚度沿x、y、z方向分解为cmj、kmj(j=x,y,z)，并设啮合传递误差为ej(j=x,y,z)，则x和z向的啮合力可以表示为[7]：

kmy(yp-yg+θpzRp+θgzRg-ey)

(2)

Fz=

cmz[zp-zg-tanβ(yp-yg+θpzRp+θgzRg)-ez]

(3)

进一步，设斜齿轮的端面压力角为αt，则x向啮合力可以表示为：

Fx=

cmx[xp-xg-tanαt(yp-yg+θpzRp+θgzRg)-ex]

(4)

最终该系统的12自由度动力学方程可以表示为：

(5)

其中mp、mg分别为主、从动齿轮的质量；Ipj、Igj(j=x,y,z)分别为主、从动齿轮绕x、y和z轴的转动惯量；Rp、Rg分别为主、从动齿轮的节圆半径；kpj、kgj(j=x,y,z)分别为主、从动齿轮的支承刚度；cpj、cgj(j=x,y,z)为主、从动齿轮的支承阻尼； 分别为主、从动齿轮对应于x、y方向扭摆自由度的阻尼系数和刚度系数；Tp、Tg为作用在主、从动齿轮上的外载荷力矩。

在多体动力学软件Simpack中，根据上述耦合动力学模型，利用表1所示的几何参数建立斜齿轮副模型，轮轴和支承部分将在与整车模型的耦合中完成。

表1　齿轮传动系统参数

为了计算齿轮箱箱体的动应力，还需要建立完整的箱体柔性模型。考虑到有限元软件ANSYS与Simpack对接性，需要预先建立齿轮箱有限元模型以备导入到Simpack中。在Solidworks中建立齿轮箱几何模型，导入ANSYS中对箱体进行网格划分后得到122 598个单元和213 951个节点。

1.2　车轮扁疤模型

车轮扁疤主要是由车轮打滑擦伤或不正常制动所导致的，在形成初期，擦伤区域表现为车轮的弦线，边界轮廓过渡不平滑。而随着车辆的持续运行，新扁疤的棱角会被迅速磨圆从而发展成为一种类似圆弧的旧扁疤，这种旧扁疤的局部外形可以通过式(6)表示[8]：

(6)

其中Df为有效擦伤深度，L为车轮擦伤长度。

将车轮滚动圆半径减去扁疤深度即可得到扁疤车轮的轮廓外形，如图2所示。

图2　车轮扁疤局部外形

利用Simpack的输入函数模块将扁疤车轮外形函数导入到模型中并建立轮轨接触关系，从而得到扁疤车轮模型，文中的扁疤设置在车辆的一位轮对上，且两轮的扁疤无相位差。

1.3　整车模型

为了在计算中考虑整车动力学效应，利用多体动力学软件Simpack建立了整车动力学模型，车辆系统由车体、枕梁、构架、电机及吊架、轴箱、主动小齿轮、从动大齿轮和齿轮箱箱体等部件组成，共86个刚体自由度和12 000个包含在柔性体内的节点自由度。车辆系统的拓扑图如图3所示。其中，0、2、7号铰分别为固定约束单元、旋转铰单元和通用轨道较单元(Simpack中专门用来描述结构沿轨道方向运动的铰接单元)。

考虑斜齿轮副模型的边界条件，通过用齿轮箱轴孔处铰接单元、车轴与轴箱处的力元代替斜齿轮弯-扭-轴-摆耦合动力学模型中的支承部分，并将前面在Simpack中建立的斜齿轮副模型的主动轴连接到牵引电机的输出轴，将车轴与从动齿轮连接，从而实现将将前文所述弯-扭-轴-摆耦合动力学模型嵌入到整车模型中。利用Simpack中的FBI(Finite Body Input)接口模块，将齿轮箱有限元模型通过在轴孔处进行节点铰接和在C型托架处建立悬挂力元的方式与整车模型连接，从而实现刚柔耦合的齿轮传动系统的完整建立。此时，齿轮传动系统的内部激扰可以通过力和扭矩等形式由力元和铰接单元传递到齿轮箱及其以外的其他车辆部件上，同时，外部激扰也通过齿轮箱系统的边界传递到其内部从而对齿轮副啮合及齿轮箱振动产生影响。装配在整车上的齿轮箱和整车刚柔耦合模型如图4所示。

图3　车辆系统拓扑图

2　计算结果分析

针对前面建立的整车动力学模型和车轮扁疤模型，车辆以300 km/h的速度运行在施加了京沪轨道谱的直线线路上，通过计算得到了齿轮箱传动系统在不同扁疤长度条件下的响应。

图4　整车动力学模型及 齿轮箱系统细节图

2.1　啮合传递误差分析

啮合传递误差是用来描述齿轮传动不平稳性的参数[9]，在车轮扁疤的故障工况研究中引入这个参数，可以清晰的观察到车轮扁疤对齿轮传动平稳性的影响。啮合传递误差的定义为：在齿轮副受外载激扰的啮合过程中，由于齿轮副存在的制造、装配误差及外部动态激扰等原因，该轮齿在啮合线方向相对理想啮合点存在的一个偏移量。它在仿真计算中可以用式(7)表示：

e(t)=Rb1φ1-Rb2φ2

(7)

式中Rb1、Rb2分别为主、从动齿轮的基圆半径；φ1、φ1分别为主、从动齿轮的实际转动角。

在计算模型中采用的齿轮模型为几何理想齿轮，没有制造与安装误差，故啮合传递误差主要来自车辆运行过程中对齿轮传动系统的激扰导致的齿距误差。图5给出了计算得到的齿轮传递误差，从图中可以看出，随着扁疤激扰的增大，动态传递误差产生了类似脉冲冲击的响应，在最恶劣的工况下，轮齿的动态传递误差从8.8 μm 增加到了25.3 μm，较正常工况增加了1.9倍。由此可见扁疤冲击对于轮齿啮合传递误差具有显著的增大作用，且齿距误差的增大甚至将导致啮合脱离，不利于轮齿平稳啮合。

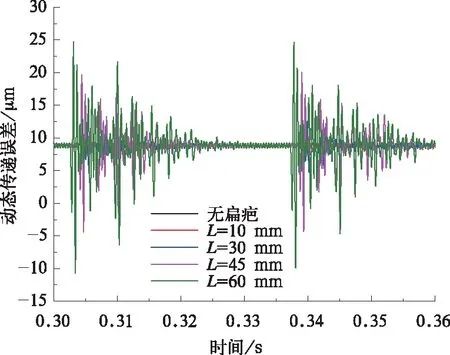
图5　啮合传递误差曲线

2.2　齿轮副最大接触应力分析

啮合传递误差能够表现齿轮副啮合的平稳性，而最大接触应力则可以反映齿轮副啮合的力学状态。

图6　齿轮副最大接触应力曲线

图6给出了不同工况下的最大接触应力曲线，图中在没有经历扁疤冲击的区段内，可以明显观察到周期性的规律，这与啮合过程中参数的时变特性是对应的。当齿轮副受扁疤冲击时，可以观察到曲线中对应区段发生了明显变化。而当扁疤脉冲冲击足够大时，从动(大)齿轮产生了较大的跳动位移，从而导致齿轮副中心距增大，使得实际啮合线段长度小于基圆齿距，定传动比的连续传动中断[10]。这将造成轮齿脱啮合的冲击。此时在图中表现出的现象是最大接触应力时域曲线中出现0值。同时大尺寸的扁疤冲击导致最大接触应力从正常工况的399 MPa增加到631 MPa，增大了0.6倍，表明车轮扁疤对啮合接触应力的平稳性产生了明显的影响。

2.3　箱体动应力分析

高速列车齿轮箱箱体采用薄壁铸铝合金结构，其固有模态的振型多样且频率分布范围较广。由于扁疤冲击近似于脉冲信号，而脉冲信号在频域范围内具有广泛分布性，会容易激起特定频率的箱体共振。本节根据前面建立的箱体有限元模型，并在整车模型中提取箱体边界载荷谱，进行有限元瞬态分析得到箱体动应力。

齿轮箱在线路服役过程中多次出现裂纹，其位置多为油位观察孔附近和箱体肋板处。图7为扁疤长度为30 mm时箱体的应力云图，此时车辆的轮轨垂向力恰好超过170 kN，达到了安全运行的临界状态，故选为典型工况进行分析。可以看出，在这一工况下，危险区域的等效应力达到了21.8 MPa，箱体的油位观察孔和包含散热肋板的箱体底部(简称：箱体底部)应力和变形较大，这与工程中的箱体裂纹多发区域是一致的，说明车轮扁疤的存在对箱体裂纹起恶化作用。

图7　齿轮箱箱体等效应力云图

为了对比箱体高应力区域的频率成分及与之相关的激扰来源，图8给出了这些区域的垂向应力频谱图，其中图8(a)为无扁疤工况，图8(b)为有扁疤(30 mm)的工况，它们是对时域曲线中的平均值进行去除后再进行傅里叶变换得到的，纵向和横向应力频谱图与垂向具有类似的特征，不再赘述。从图8(a)、(b)对比中可以看出，当车轮存在扁疤缺陷时，箱体的垂向应力频谱在574.6 Hz和979.6 Hz频率处出现了两处明显的峰值，说明车轮扁疤的脉冲激扰会引起箱体在特定频率上的共振。同时，注意到这两处不同频率的峰值分别对应于箱体的油位观察孔和箱体底部，这是由不同固有频率的相应模态决定的。574.6 Hz对应于箱体的一阶模态，表现为下箱体的扭摆，故在图中与下箱体的油位观察孔测点的峰值相对应，而979.6 Hz对应于箱体的三阶模态，表现为大齿轮端箱体的扭摆，将引起箱体底部的变形与应力集中，故在图中与箱体底部测点的峰值相对应。另外，可以发现，由于考虑了齿轮传动系统啮合的内部激扰，箱体应力响应频谱中可以捕捉到啮合频率(2 448.6 Hz)的成分。但对比图8(a)、(b)发现，与外部

图8　箱体垂向应力频谱图

激扰相关的两个频率主峰值所占的能量比重远大于箱体内部啮合激扰的能量，说明车轮扁疤激扰引起的能量在响应中占更大的比重，对箱体强度有更重要影响。

在不同工况的计算结果中，对箱体危险点处的等效应力进行提取，得到了不同工况时箱体的最大动应力曲线，如图9所示。可见随着扁疤长度的增加，各个测点的最大动应力是增大的，但箱体上不同测点的最大动应力与扁疤长度的正相关性是不同的。由于外部激扰没有激起小齿轮轴承座附近的相关共振模态，小齿轮轴承座处的应力变化并不明显。而在引起了局部共振的油位观察孔和箱体底部，最大动应力与扁疤长度的正相关性比小齿轮轴承座处更大。这意味着在进行箱体强度分析时，需要与模态分析相结合对不同区域进行分析。同时需要指明的是，当扁疤长度达到60 mm时，箱体上危险点的应力为140 MPa，没有超过箱体的许用应力(200 MPa)，说明它在瞬时是符合强度要求的。但这样高频高幅值的应力载荷会很容易在短时间内引起箱体的疲劳破坏，在服役过程中引起的疲劳破坏问题应进一步关注和研究。

图9　不同工况时箱体最大动应力

3　结　论

通过在故障工况下建立包含齿轮传动系统的高速列车刚柔耦合动力学模型，计算得到了以下结论：

(1) 车轮扁疤对于高速列车齿轮传动系统的平稳啮合有恶劣影响。具体表现为：在动态传递误差和最大接触应力曲线上有明显脉冲冲击体现，当激扰达到一定程度时将引起齿轮副瞬时啮合脱离，从而导致啮合冲击的产生。

(2) 箱体不同位置处的应力与车轮扁疤长度的正相关性强弱因是否激起局部共振及相应固有模态的类型而不同，其中箱体底部和油位观察孔处与车轮扁疤长度的相关性较高，应力和变形较大，为危险区域。

(3) 车轮扁疤的激扰能量远大于箱体内部激扰能量，对箱体动应力水平的影响很大。此外，危险区域的应力频谱特性显示其与车轮扁疤相关，所以相比内部激扰，车轮扁疤引起的动态响应对工程运用中箱体裂纹的形成存在更大的影响，需要重点关注。